远区台风“三巴”对长江口波浪动力场的作用机制

任剑波 , 何 青 沈 健, 徐 凡 郭磊城 谢卫明 朱 磊

(1. 华东师范大学 河口海岸学国家重点实验室, 上海 200241; 2. 杭州绍逸环境技术有限公司, 浙江 杭州310007; 3. 美国威廉玛丽学院 弗吉尼亚海洋研究所, 美国 弗吉尼亚州 23062; 4. 中山大学 海洋科学学院,广东 广州 510275)

长江口地处太平洋西岸, 每年 7—9月份, 都会受到台风袭击, 平均每年有 2～3个台风对长江口及其邻近海域产生影响, 最多时一年可达5～6个[1]。台风引起的狂风巨浪, 常常造成沿海风暴潮、河口海岸侵蚀和航道骤淤, 据统计, 每年风暴潮造成的经济损失高达上百亿元, 台风引起的航道骤淤量为 200万～800万m3, 占航道年回淤总量的贡献率最大可达50%[2],历史上曾出现一次台风使北槽航道全线淤浅 0.5 m的记录[3]。

一般认为远区台风与长江口的距离远超七级风圈半径, 不会对长江口水动力和泥沙运动产生影响,如远区台风0207号“卡奴”、0215号“鹿莎”和0217号“杰拉华”。然而, 根据贾晓[4]、孔令双[5]等研究成果可知, 2012年远台风区“三巴”造成北槽深水航道近200万m3的骤淤量, 其影响已经超过部分登陆型和近海型台风, 如“鹿莎”和登陆型台风“森拉克”的叠加淤积量仅为190万m3[2], 1323号台风“菲特”期间造成的淤积量仅为166万m3[5]。这些数据表明远区台风对长江口的动力场和泥沙运动的影响也是不容忽视的。

本文从波浪运动的角度, 研究了远区台风对长江口波浪动力的作用机制。采用美国国家环境预报中心(NCEP)的FNL风场和台风模型风场生成的融合风场, 利用第三代波浪模式 SWAN对“三巴”台风期间的长江口波浪场进行了模拟反演, 利用定点观测资料和JASON-2卫星高度计资料对模型进行了验证, 计算了远区台风“三巴”对长江口波浪场和波能耗散的影响, 从波浪切应力和泥沙侵蚀能力的角度研究了泥沙侵蚀率分布规律, 有助于了解远区台风期间长江口泥沙运动和地貌演变的规律。

1 研究区域

1.1 长江口

长江口面临东海(图 1), 受径流、潮汐和波浪的共同作用, 是典型的高浊度河口。上游来水丰沛, 年径流总量为 9.034×108m3, 径流量在年内呈现明显的季节性变化, 5—10月为洪季, 占全年径流量的71.7%。长江口平均潮差为2.7 m, 受地形约束, 潮流多为往复流, 垂线平均流速变化范围为1.0～2.0 m/s。

图1 模型计算区域、观测站位和台风路径图Fig. 1 Numerical model domain, locations of wind and wave gauging station, and path of typhoon “Sanba”

长江口波浪以风浪为主, 波浪方向变化具有明显的季节性, 夏季以 ESE—SSE向浪为主, 冬季以NW—N向浪为主。长江口引水船站多年平均波高为0.9 m, 平均周期为3.8 s[6]。同时, 涌浪也时有出现,冬季以东北向涌浪最多, 春、夏、秋三季以E向涌浪为主, 最大波高常发生在台风期间, 海面呈现风浪和涌浪二者共存的混合浪, 最大浪高可达6 m, 波浪周期可达 5～6 s。

1.2 1216号台风“三巴”

2012年16号台风“三巴”是典型的远区台风, 台风中心距离长江口最小距离约580 km(图1), 远大于七级风圈半径。“三巴”于9月11日8时在菲律宾以东洋面生成, 次日14时加强为强热带风暴, 20时迅速发展为台风, 中心气压达 965 hPa, 近中心最大风力13级(38 m/s), 13日17时进一步发展为超强台风, 14日8时台风中心到达钓鱼岛东南方向洋面上,近中心最低气压达915 hPa, 近中心最大风速达17级以上(60 m/s)。16日台风进入东中国海, 移速明显加快, 此后台风持续向北移动, 17日登陆韩国南部。受台风影响, 长江口、杭州湾和浙江中北部沿海均有7～9级大风和大浪。

2 研究方法

2.1 台风气压场和风场模型

波浪由台风风场作用下产生和发展的, 波浪模拟的精度取决于气压场和风场的精度。研究表明, 在台风中心附近, 台风模型风场能够较好的反映内部风场特征, 在外围区域, 由于同时受到其他天气系统的影响, 模型风场往往不能很好的描述外围风场特征。本文采用美国国家环境预报中心(NCEP)的FNL风场和台风模型风场两者的融合风场。FNL资料汇总了全球资料同化分析系统及其他大量的观测资料和卫星反演资料, 空间分辨率为 1°×1°, 时间间隔为6 h。台风模型风场由梯度风场和移动风场组成,王喜年[7]经大量研究认为(1)—(6)式能够比较真实描述东海气压场和台风风场。

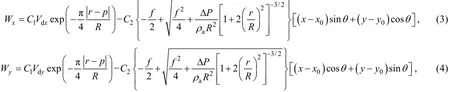
当 2R≤r≤∞:

式中, C1、C2是经验常数, θ是流入角, ρa是空气密度,f是科氏力参数, P为气压值, P∞为外围气压, P0为中心气压, r是计算点距离台风中心距离, R为最大风速半径, Wx、Wy分别为台风风速在x、y方向上的分量,Vdx、Vdy为台风移动速度在x、y方向上的分量。

融合风场能够有效解决NCEP/FNL资料在台风中心附近风速偏小和模型风场的外围风场准确度不高的缺点。两种风场通过下式[8]进行融合:

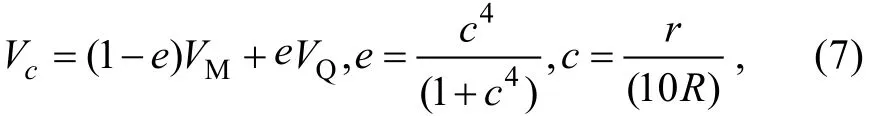
式中, VM为台风模型风场计算风速, VQ为NCEP/FNL风场, r为网格点与台风中心的距离, e, c为系数, R为最大风速半径, 由下式[9]计算:

2.2 波浪模型SWAN

SWAN模式(Version 41.31)是由荷兰代尔夫特理工大学开发的第三代海浪预测模式[10], 采用基于Euler近似的二维波作用量N(σ, θ)平衡方程描述随机波浪场, 模式中考虑了风能输入、白帽耗散、底摩擦、三波、四波非线性相互作用, 以及波浪遇水工构筑物的传播、反射和绕射等物理过程, 被广泛用于近岸、湖泊、河口等水域。SWAN曾被多次应用在长江口海域[11]。其控制方程为:

式中, N(σ, θ)为波作用量密度, N(σ, θ)=E(σ, θ)/σ, σ为相对频率, θ为波向。方程中第一项表示波作用量N随时间的变化率, 第二、三项表示在地理空间 x、y方向上以速度 Cx、Cy的传播, 第四项在频率空间 σ的传播, 第五项表示在谱分布方向 θ空间的传播。S表示能量源汇项, 包括模式采用全隐式有限差分格式离散控制方程。

风能输入是波浪模式中的源项, 采用Phillips提出的共振机制和Miles提出的反馈机制进行描述, 前者适用于风浪的发生和初始阶段, 后者适用于风浪成长的主要阶段。风拖曳系数CD根据下式[10]计算:

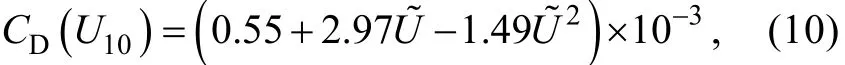
波浪传播过程中的能量耗散主要包括白帽耗散、底摩擦耗能、深度诱导波破碎和波—波非线性作用。白帽破碎是波浪在深水区域占主要地位的能量耗散过程, 采用 Hasselmann提出的基于脉冲原理的模式描述, 在中等深度和浅水水域, 采用经验性的 JONSWAP公式描述底摩擦对波浪能量的耗散作用。模型中同时考虑了波-波相互作用。

SWAN模型计算区域包括东海、黄海、渤海(图1),采用正交曲线网格进行空间离散, 网格呈扇形结构设计, 扇心取在长江口, 网格步长从扇心至扇缘逐渐增大, 长江口网格步长约为200～300 m, 边界处步长约9 000 m, 能够同时兼顾大区域模拟和高空间分辨率的要求。计算时间段为“三巴”台风期间, 2012年9月12日—9月18日。频率空间起止范围为0.035～1.5 Hz, 分24个频段, 方向空间起止范围为0°～360°,分辨率为15°。

2.3 模型验证

风场和波浪场模型验证采用“三巴”台风期间长江口风况观测站(牛皮礁站, 长期站)和波浪观测站(底座式观测站, 位于横沙浅滩)资料(图1), 由于受到台风期间强烈的水沙运动影响, 底座式观测站波浪资料有效时间段为2012年9月12日—9月16日。为进一步评估模型的合理性和准确性, 同时收集了JASON-2卫星高度计的风和有效波高资料。JSAON-2卫星高度计是T/P和JASON-1高度计的延续, 于2008年6月发射升空, 重访周期10天, 波高测量精度0.5 m, 风速精度1.5 m/s。“三巴”台风期间, JASON-2的第154周期240轨道正好经过计算区域, 时间为9月15日11时48分—50分(GMT), 共计112个观测点(图1)。

验证结果表明, 模型计算结果与实测资料在相位和极值上均较为符合, 风场和波浪模型能够准确的重现台风期间风和波浪过程(图2)。

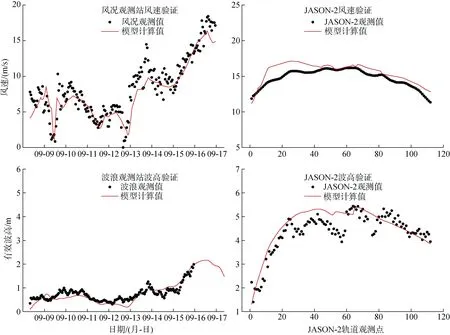
图2 实测值和模型计算值对比图Fig. 2 Comparison of observation data and numerical model results

2.4 波浪切应力和泥沙侵蚀率

底部切应力常被用来研究泥沙侵蚀的动力机制[12-13], 侵蚀能力随着切应力增大而增强, 当波浪产生的切应力(τw)超过泥沙临界起动应力时, 泥沙发生再悬浮, 海床发生侵蚀。波浪产生的底部切应力(τw)由式(11)计算:

式中, ρ是海水密度, fw是波浪摩阻系数, uw为底部最大轨道流速, Aw(=uwT/2π)为底部波浪水质点最大位移, T为底部波浪周期, ks(=2.5d50)为Nikuradse粗糙高度, d50为泥沙中值粒径。

泥沙侵蚀率 E和侵蚀能量 Eflux可通过下式[14]计算:

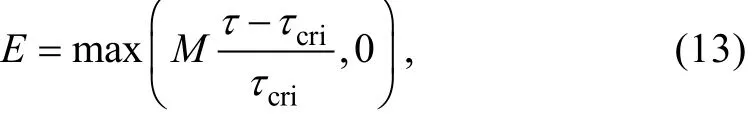
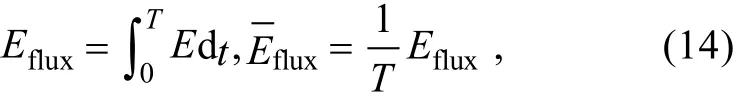
式中, M=5×10-5kg/(m2·s)[15]为侵蚀率系数, τcri=0.5 Pa[15]为长江口平均临界起动应力, Eflux[kg/(m2·s)]和[kg/(m2·s)]分别为台风影响期间T时间内总的侵蚀通量和平均侵蚀率。

3 结果与讨论

3.1 波浪动力场

图3为2012年9月16日14: 00台风中心位于长江口东南侧650 km处时的瞬时风场和有效波高分布。台风风场呈“气旋型”分布, 台风行进方向的右侧风场大于左侧风场, 最大风速可达45～55 m/s。受“气旋型”风场影响, 波浪场也呈现“气旋型”分布,台风中心附近波高最大, 最大有效波高可达13～15 m,右侧波高大于左侧。长江口受NE—N风控制, 风速为15～18 m/s, 有效波高为 1～2 m。

图3 2012年9月16日14时, 计算海域台风风场和风速分布、有效波高和波向分布Fig. 3 Spatial distribution of wind speed and wind vector, significant wave height and wave vector at 14: 00 on Sep. 16, 2012

“三巴”台风产生的波浪由NE—N方向传入长江口, 有效波高Hsig在20 m以深水域与等深线分布基本平行(图 4), 但等波高线走向与波浪传播方向并不完全垂直, 进入长江口水域后, 由于水深浅化效应, 波向逐步偏转与等深线垂直。由于波浪传播过程中能量的衰减, 有效波高由10 m等深线的3 m衰减为5 m等深线的2 m。横沙浅滩和北堤向东侧海域外凸的地形在一定程度上阻挡了波浪向西侧传播, 波高衰减幅度相对较大, 等波高线密度加大, 表明波浪在行经横沙浅滩和北堤向东侧海域时发生了较多的能量衰减。波浪经北堤绕射后继续向北港、南槽等水域传播。在崇明东滩、横沙浅滩及九段沙浅滩,因水深较浅且滩面宽广, 底摩擦力耗能显著, 有效波高逐步衰减为0.5～1.5 m。波长的分布与有效波高相似, 波浪进入长江口后, 波长发生衰减, 由-20 m等深线处的40 m减小为5 m等深线处的20 m。

在常规天气下, 长江口波浪主要为风浪, 周期一般为3～4 s。在台风期间, 长江口波浪场受到涌浪的影响, 表现为风浪、涌浪共存的混合浪形式, 涌浪的传入使波浪周期显著增大, 表明波浪能量的增强。长江口外 10 m等深线水域波浪底部周期 Tb一般为7～9 s, 是常规天气下波浪周期的 3～4倍, 波浪向上游水域传播过程中, 由于能量耗散周期逐渐减小至5～7 s。

近底层最大轨道流速 Ubot的分布格局显著区别于波高、波长和周期的分布, 与相对水深有关。在水深大于30 m的东侧水域, 波高和周期较大, 但水深大于波浪有效作用深度, 波浪无法作用到海底, 最大轨道流速一般不超过0.2 m/s。在水深小于30 m以浅水域, 存在两个最大轨道流速的显著增大区, 分别位于在横沙浅滩东测和崇明东滩东侧水域, 以及北槽口外海域, Ubot平均为0.8 m/s, 最大可达1.1 m/s。波浪在进入北港、南槽等水域后, 由于底部摩擦力和波浪破碎耗能, Ubot逐步减小为0.1～0.2 m/s。Ubot为波浪底部轨道振幅 Aw与底部周期 Tb的比值, Ubot取决于 Hsig、Tb和 sinh-1kh, k 为波数(k=2π/λ), h 为水深。sinh-1kh的分布形态与 Ubot具有很强的一致性, 表明水深和波长的比值 h/λ决定了底层波浪流速的分布,也决定了底部泥沙再悬浮的分布格局, 当水深一定时(h＜2λ), 波长(周期)越大, 底层流速越大, 因此长周期涌浪的传入有利于增大底部流速。

波浪引起的底部切应力分布与 Ubot分布格局相似, 横沙浅滩东测和崇明东滩东侧5～10 m水域是高切应力分布区(3～6 Pa), 北槽口外水域切应力可达3～4 Pa, 均远大于泥沙临界起动切应力0.5 Pa[15]。

3.2 波浪能量耗散

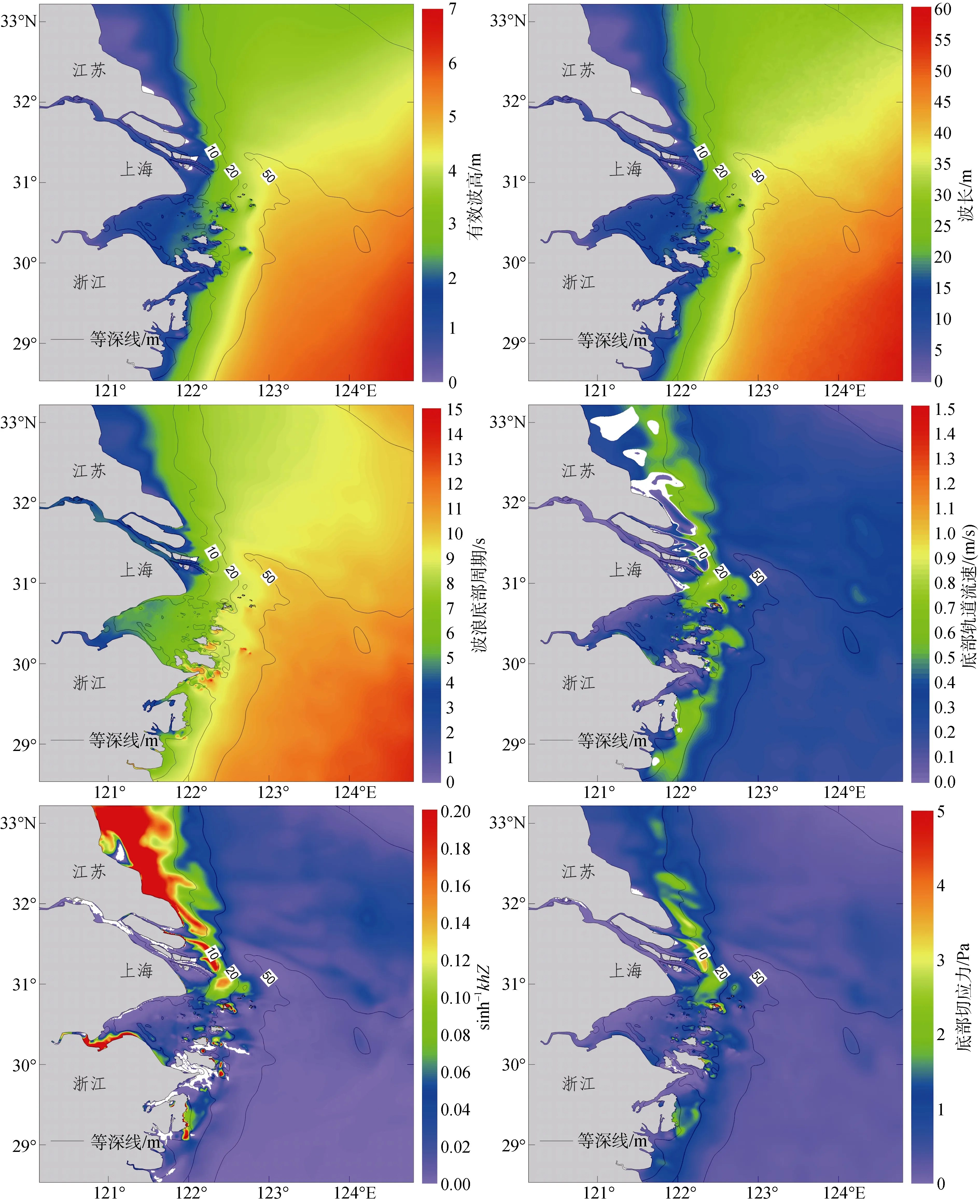
图4 2012年9月16日14时, 长江口及邻近海域波浪有效波高、波长、底部周期、底部轨道流速、sinh-1kh和底部切应力分布Fig. 4 Spatial distribution of significant wave height, wave length, wave period near the bottom, wave orbital velocity, sinh-1kh,and wave-induced shear stress at 14: 00 on Sep. 16, 2012

波浪能量耗散是风-波浪能量平衡的三大机制之一, 由白帽破碎、底摩擦耗能和水深诱导的破碎耗能三部分组成[11], 对波浪动力场的空间分布起着重要作用。在深水区域, 波浪在风能持续输入下不断成长,波高增大, 波面变陡, 当波陡超过极限波陡时波浪发生破碎, 波浪成长受到限制。白帽破碎引起的能量耗散量由台风中心的 60 W/m2向近岸逐渐递减为约1 W/m2, 在30 m以深水域, 白帽破碎占总耗散能量的 80%以上, 因此其是维持深水区波浪能量平衡和限制波高成长的主要机制, 决定了波高, 波长和周期等波浪要素的分布格局。在长江口横沙东滩和崇明东滩东侧5～10 m水域, 白帽破碎耗散为0.1～1.1 W/m2,占比 8%～30%。底摩擦耗能是波浪引起的底部水质点运动与海底发生摩擦作用产生的, 其分布趋势与白帽破碎耗能相反, 从台风中心向四周缓慢增大,在20 m以深水域耗能量不超过0.1 W/m2。当波浪传播到水深较浅的长江口时, 波浪和海底的相互作用开始增强, 波浪底部轨道流速逐渐增大, 底摩擦耗能逐渐占据主导, 特别是横沙东滩和崇明东滩东侧2.5～10 m水域, 底摩擦耗能在1.0～1.8 W/m2, 占总耗能的30%～50%。同时, 由于水深变浅导致波高增大,当波高超过最大波高Hm(=γh, γ=0.8为破碎系数[10], h为水深)时, 横沙东滩和崇明东滩以东5 m等深线附近波浪发生破碎, 耗能量为2.0～3.5 W/m2, 占总耗能的 50%～60%。因此, 底摩擦耗能和水深诱导的破碎耗能是导致长江口横沙东滩和崇明东滩波高减小的主要因素。

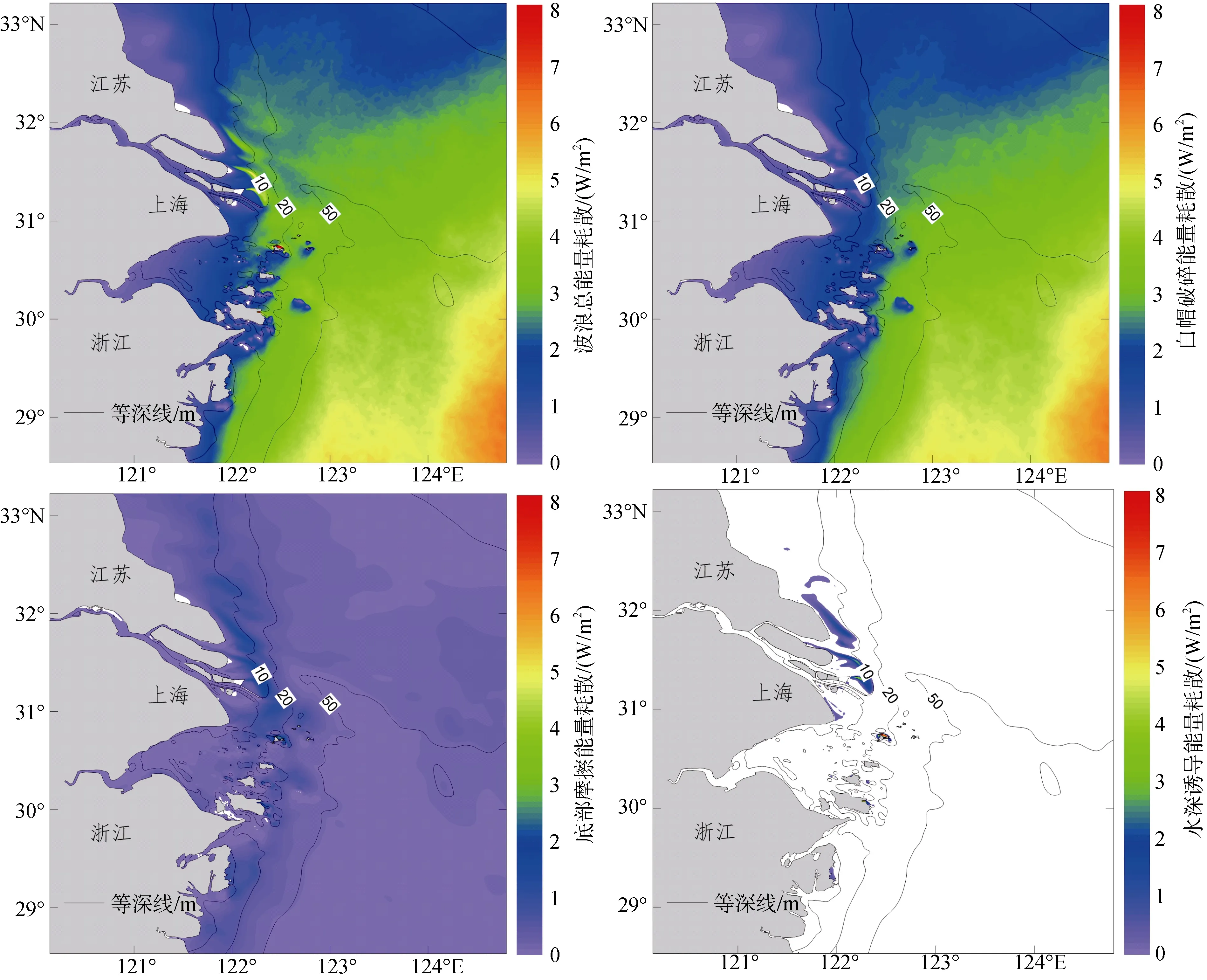
图5 2012年9月16日14时, 长江口及邻近海域波浪总能量耗散、白帽破碎能量耗能、底部摩擦能量耗能、水深诱导能量耗散Fig. 5 Spatial distribution of total energy dissipation, whitecapping dissipation, bottom friction dissipation, and depth-induced dissipation in the CJE and adjacent sea at 14: 00 on Sep. 16, 2012

3.3 波浪谱特征变化

图6 为2012年9月15日14时至17日06时波浪观测站的频谱图。15日14时, “三巴”发展成为超强台风, 台风中心最大风速55 m/s。长江口开始受到台风风场影响, 观测站风速呈现显著增大趋势,根据频谱图可知, 15日14时观测站频谱类型为单峰型, 谱峰能量约10 000 J/(m2·Hz), 谱峰频率为0.17 Hz,对应的谱峰周期为5.9 s。15日22时至16日06时, 随着台风的北移, 台风中心与长江口的距离逐渐减小为 700 km, 谱形进一步变窄, 谱峰能量显著增大且更加集中, 谱峰频率从0.15 Hz(对应周期为6.7 s)向低频区域0.13 Hz(对应周期为7.7 s)移动。14时, 谱峰能量达到最大值28 778 J/(m2·Hz), 谱形尖而窄, 谱峰频率为0.12 Hz, 对应周期为8.4 s。14时至22时,谱形变宽, 谱峰能量逐步降低, 但谱峰频率仍向低频区域移动(0.11 Hz, 对应周期为9.1 s)。17日06时,台风在韩国登陆前夕, 观测站谱形呈现双峰型, 谱峰频率分别为0.12 Hz(周期8.4 s)和0.25 Hz(周期4.0 s),表明存在两个相互独立的波浪系统, 根据波浪系统识别法(JP方法), 谱峰之间的“波谷”可以视作两个波浪系统的分割频率, 小于分割频率0.19 Hz的波浪系统为涌浪, 大于0.19 Hz的为风浪。第一个波浪系统谱峰频率为 0.11 Hz, 属涌浪系统, 第二个谱峰频率为0.25 Hz, 对应周期为4 s, 与长江口引水船站多年平均周期相近, 为风浪系统。

图6 2012年9月15日14: 00至17日06: 00波浪观测站的波浪谱变化过程Fig. 6 The variation of wave frequency spectrum from 14: 00 on Sep. 15 to 06: 00 on 17, 2012

以上分析表明, 2012年15日14时至16日22时,波浪谱形为单峰谱, 谱峰频率从0.17 Hz逐渐减小至0.11 Hz, 谱峰能量更加集中, 说明波浪场以涌浪为主导。随后, 由于台风强度减弱, 波浪场表现为涌浪略占优势的混合浪。

3.4 波浪引起的泥沙侵蚀率

图 7为“三巴”台风影响期间长江口波浪平均侵蚀率, 及其与潮流平均侵蚀率[13]的比值α分布。横沙浅滩东测和崇明东滩东侧5～10 m等深线之间的水域, 以及北槽口外 10～20 m等深线海域是泥沙侵蚀率最大的水域, 平均侵蚀率分别为1.5×10-4kg/(m2·s)和0.8×10-4kg/(m2·s), 表明该水域泥沙极度容易波浪侵蚀作用。横沙浅滩东测和崇明东滩东侧5～10 m等深线水域, α值在5～12之间, 最大可以达到200, 平均值为 15, 发生在横沙浅滩东侧测 10 m等深线水域。北槽口外10～20 m等深线海域α值在1.1～1.8, 平均为 1.3。以上结果表明, 台风浪造成的侵蚀作用是潮流侵蚀作用的15倍, 这与Ren[16]在江苏沿岸观测到的结果基本一致, 可见台风浪在泥沙侵蚀和河口地貌塑造中的重要作用。

为进一步研究远区台风对长江口泥沙侵蚀的影响, 本文分别计算了不同台风强度条件下泥沙侵蚀分布, 在不改变“三巴”台风参数如路径、气压场和移动速度的基础上, 将其风场乘上一个系数 β表示不同的台风强度, 如β=0.6表示台风强度为“三巴”台风的 60%。不同台风强度下长江口泥沙侵蚀率和风速过程见图8。

当β=0.6时, 长江口平均风速为7.5 m/s, 最大风速为10 m/s, 风速＞8 m/s的持续时间为35 h, 泥沙侵蚀区域主要发生在横沙浅滩和崇明东滩水域, 平均侵蚀率为 0.8×10-5kg/(m2·s), 其他水域没有发生侵蚀。当台风强度增大到β=0.7时, 长江口最大风速为12 m/s, 风速＞8 m/s的持续时间为45 h, 平均侵蚀率增大为1.5×10-5kg/(m2·s), 横沙浅滩和崇明东滩水域连接成一片。当β=0.8和0.9时, 最大风速为15 m/s,风速＞8 m/s的持续时间为60 h, 横沙浅滩和崇明东滩水域和北槽口外水域均发生侵蚀, 前者平均侵蚀率增大为 10.0×10-5kg/(m2·s), 后者平均侵蚀率为3.0×10-5kg/(m2·s)。因此, 如果以长江口风速(或有效波高)作为是否发生侵蚀的指示因子, 当最大风速＜10 m/s, 长江口水域基本不会发生强侵蚀, 当风速＞10 m/s, 横沙浅滩和崇明东滩水域以及北槽口外水域是最容易发生泥沙侵蚀的区域。结合计算的波浪观测站最大风速和最大有效波高关系(图 9)可知, 当有效波高＞1.2 m时, 水下三角洲前沿水域开始发生波浪侵蚀。

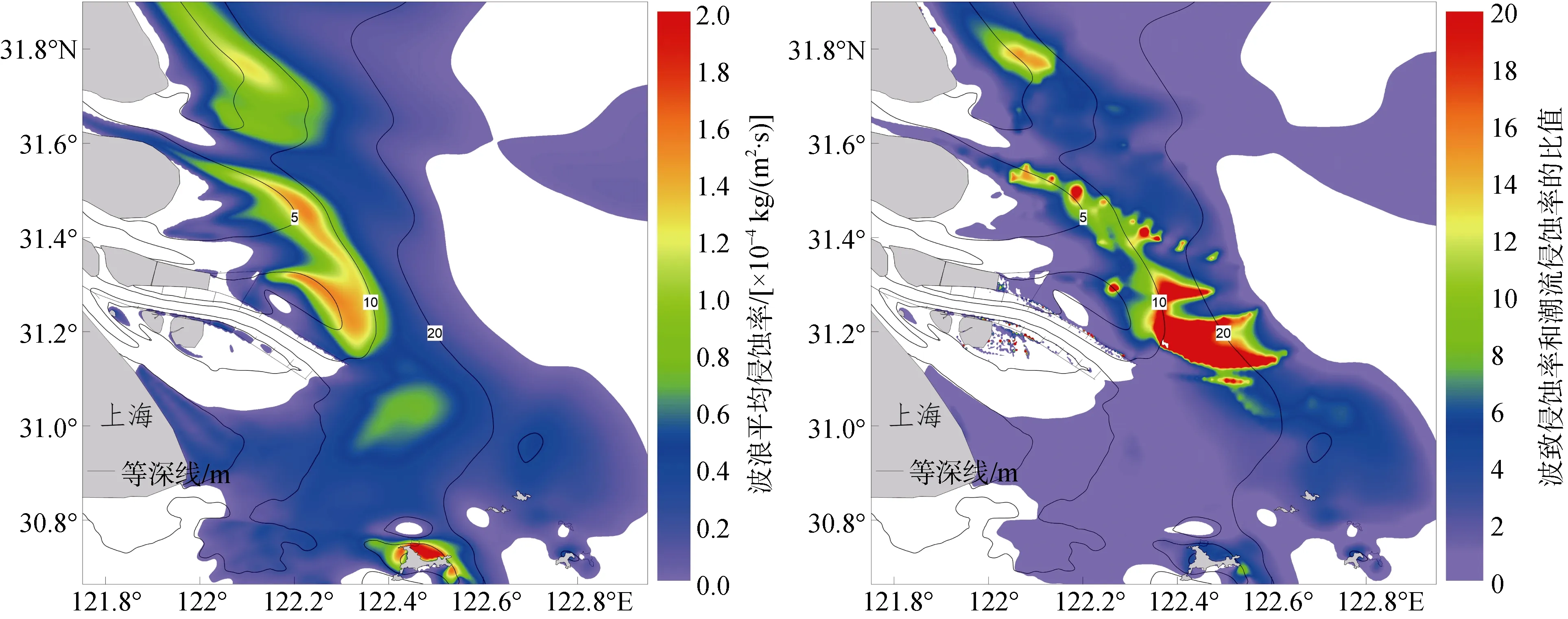
图7 2012年9月15日—9月17日, 台风浪引起的平均侵蚀率分布, 以及波致侵蚀率和潮流平均侵蚀率之比Fig. 7 Spatial distribution of wave-induced averaged erosion rates, and ratio of wave-induced averaged erosion rates to that of tide-induced ones from Sep. 15 to 17, 2012

图8 不同台风强度β下, 波浪引起的平均侵蚀率分布Fig. 8 Wave-induced averaged erosion rates under different strength of remote typhoon

图9 波浪观测站最大风速和最大有效波高关系图Fig. 9 The relationship between maximum wind speed and significant wave height

3.5 风浪和涌浪的侵蚀机制

由式(11)和(12)整理可得式(15), 底部切应力τw与近底层最大轨道流速uw、底部波浪周期T的关系如图10所示, 底部切应力τw随近底层最大轨道流速uw(式 16[10])增大而增大(图 10a), 且增幅远大于因周期增大而减小的幅度,和E(σ,θ)呈正相关, 当波长大于约10 m时,随波长增大呈现直线增大趋势(图10b)。式(15)—式(18)表明波浪周期越大, 则波长越大, 底部切应力越大; 波浪能量密度越大, 则底部切应力越大。涌浪从外海向近岸传播过程中, 由于波-波相互作用, 能量由高频向低频转换,涌浪的周期(波长)逐渐增大, 能量更加集中(图 6),因此涌浪引起的底部切应力大于风浪, 涌浪引起的泥沙侵蚀能力强于风浪。

式中h=6.5 m, 为波浪观测站水深,k=2π/λ, 为波数,λ为波长,E(σ,θ)为能量密度。

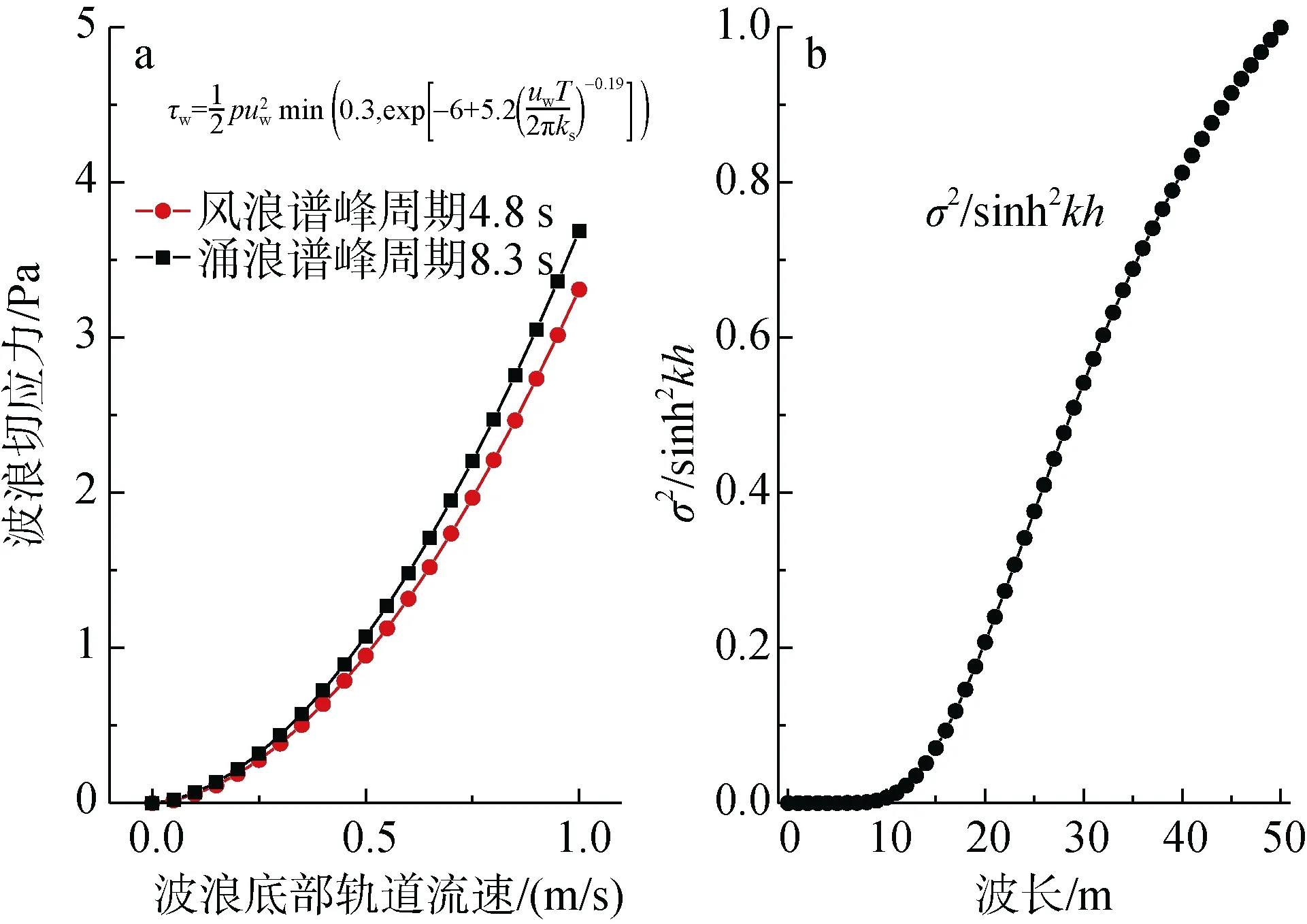
图10 底部切应力(τw)和近底层最大轨道流速uw、底部波浪周期T关系图Fig. 10 The relationship between orbital velocity and wave period near bottom

4 结论

本文围绕陆架远区台风对河口波浪动力场影响的研究命题, 利用第三代波浪模式 SWAN对台风期间长江口波浪动力的时空分布进行了模拟, 模型风场采用美国国家环境预报中心(NCEP)的FNL风场和台风模型风场生成的融合风场, 利用定点观测资料和 JASON-2卫星高度计资料对模型进行了验证, 结果表明: (1)波浪模型能够重现计算域内风场和波浪场的时空分布特征; (2)在深水区, 白帽破碎是维持波浪能量平衡和限制波高成长的主要机制, 在浅水区, 底摩擦耗能和水深诱导的破碎耗能是导致近岸水域波高减小的主要原因; (3)波浪产生的切应力分布格局与相对水深有关, 切应力增大由涌浪主导, 涌浪由外海向近岸传播过程中, 周期和波长逐渐增大,近底层轨道流速增大, 能量密度趋于集中, 是波浪底部切应力增大的主要原因; (4)与河口相距数百公里的远区台风仍然能够对长江口波浪动力场产生明显影响, 水下三角洲前缘是最容易受到波浪作用的区域。

台风期间, 长江口的动力过程是非常复杂的,径流、潮流、风生流和波浪相互作用, 波流耦合作用对泥沙的再悬浮和输移具有重要影响, 本文主要从波浪动力场角度, 研究泥沙侵蚀率分布, 对于波流共同作用下的泥沙输运, 有待在下一步的工作中完善。