斜风下板桁结合加劲梁静气动力系数试验研究

刘志文 ，易志涛 ，陈政清 ，向建军 ，李瑜 ，崔剑峰

（1.湖南大学 风工程与桥梁工程湖南省重点实验室，湖南长沙410082；2.湖南省交通规划勘察设计院有限公司，湖南 长沙410008）

随着我国交通基础设施建设的进一步推进，跨越江河、山区峡谷的大跨度桥梁逐渐成为我国桥梁工程建设的重点.流线型箱梁和桁架加劲梁是大跨度桥梁常用的两种主梁形式，考虑到运输与施工的方便，近年来桁架加劲梁在山区峡谷和公铁两用大跨度桥梁中的应用增多，如贵州坝陵河大桥、湖南矮寨大桥、湖北四渡河大桥、湖北天兴洲大桥等.

目前，关于大跨度桥梁抗风性能研究多侧重于横桥向风作用下的桥梁颤振稳定性、涡振性能与风荷载等性能[1-4].然而实际桥梁工程中，在风环境复杂的山区往往需要考虑风向不垂直于桥梁轴线的情况，即斜风作用下桥梁结构的抗风性能问题.在斜风作用下，桁架加劲梁相比实腹式主梁的风荷载特性更为复杂.Zhu等[5-6]以青马大桥为工程背景进行了斜风作用下的颤振导数测量和风攻角为-10°～+10°、风偏角为0°～35°范围内主梁的静气动力系数试验研究.结果表明，阻力系数随着风偏角的增大而减小，升力系数随风偏角变化较小，气动扭矩系数随着风偏角的增大而增大.Zhu和Xu等[7-8]建立了斜风作用下桥梁结构抖振响应理论分析方法，针对青马大桥在斜风作用下的抖振响应进行了计算，计算结果与大桥实测结果总体较为吻合.刘小兵等[9]以鄂东长江公路大桥为依托，采用风洞试验方法研究了P-K断面主梁在风偏角为0°～45°时不同攻角下的三分力系数.试验结果表明，阻力系数总体上随风偏角的增大而先增大后减小，风偏角为15°时阻力系数最大.Biggs[10]和Pagon[11]研究了风偏角对桁架梁桥横桥向风荷载的影响.结果表明，由迎风侧桁架杆件所引起的气流扰动导致背风侧桁架杆件阻力发生变化；当水平偏角为0°时，迎风侧桁架杆件对背风侧桁架杆件的遮挡作用较大，随着风偏角的增大这种遮挡作用在减小，且遮挡作用与桁架面积比有关.戴伟等[12-13]以上海闵浦大桥双层空腹钢桁架结构为工程背景采用风洞试验方法进行了风攻角为-10°～+10°、风偏角为0°～30°范围内桁架加劲梁气动力系数试验研究，并且通过对各风偏角的横向风作用下主梁静气动力系数的分解，初步探讨了桁架结构主梁斜风下静风力系数计算方法.毛文浩等[14]以洞庭湖二桥初步设计方案为工程背景，采用风洞试验方法进行了0°风攻角下0°～90°风偏角范围内桁架加劲梁气动力系数试验.结果表明，0°风攻角下桁架加劲梁顺桥向阻力系数随风偏角的增加先增大后减小.郑史雄等[15]针对倒梯形断面桁梁在0°～180°风偏角内与不同风攻角组合进行了静气动力系数风洞试验.结果表明，横桥向力系数最大值均发生在风偏角为15°左右时，顺桥向力系数最大值发生在风偏角为60°左右时；对于此类断面桁梁桥进行横桥向风致响应计算时，横桥向来风时不一定是最不利来流，且顺桥向力不能忽略.我国《公路桥梁抗风设计规范》（JTG/T D60-01-2004）[16]针对闭口箱梁给出了顺桥向风荷载系数建议值，对跨径小于200 m的桁架梁顺桥向风荷载则建议为其横桥向风荷载的0.50倍，而对于跨径大于200 m的桁架加劲梁则没有明确规定.

综上所述，关于桁架加劲梁在斜风作用下的气动参数研究在风攻角、风偏角考虑方面尚不全面.由于桁架加劲梁空间结构较为复杂，在斜风作用下其气动力系数、气动性能更为复杂.斜风作用下顺桥向风荷载往往对桥塔、梁端伸缩缝和塔梁交接处阻尼器等的设计具有重要影响，故合理确定桥梁顺桥向风荷载系数对大跨度桥梁抗风设计至关重要.

本文以洞庭湖二桥为工程背景，采用风洞试验方法进行了斜风作用下板桁结合加劲梁在不同风攻角时气动力系数试验研究，并考虑不同长度补偿段模型对试验结果的影响，最后将静气动力系数试验结果与国内外规范进行了比较.

1 试验概括

1.1 工程简介

岳阳洞庭湖二桥是杭瑞高速公路湖南段跨越洞庭湖的一座特大桥，主桥结构为双塔双跨钢桁架加劲梁悬索桥，桥跨布置为1 480 m+453.6 m=1 933.6 m，桥梁结构总体布置如图1所示.加劲梁采用板桁结合梁，桁架梁高为9 m，桁架梁宽为35.4 m，桁架梁标准节间长度16.8 m，钢桁架梁标准断面如图2所示.主缆垂跨比为1/10，主索中心距为35.4 m.索塔为混凝土门式塔，岳阳侧高为203.088 m，君山侧高为206.088 m.

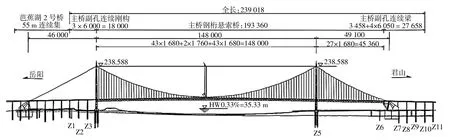
图1 岳阳洞庭湖二桥总体布置示意图（单位：cm）Fig.1 General layout of the second bridge of Yueyang Dongting Lake（unit：cm）

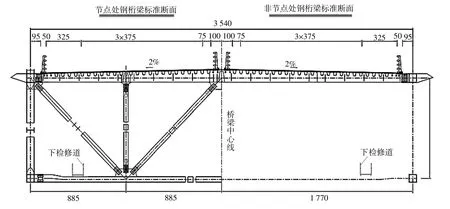
图2 岳阳洞庭湖二桥板桁结合加劲梁断面图（单位：cm）Fig.2 PTCSG cross section of the second bridge of Yueyang Dongting Lake（unit：cm）

1.2 试验装置与工况

为实现桁架加劲梁气动力系数测试时风攻角方便调节，设计并制作了可实现攻角调节的试验支架，如图3所示.加劲梁测力试验模型几何缩尺比取λL=1∶70，加劲梁试验模型由测力试验模型段和两端补偿段试验模型组成，测力试验模型段总长度L=1 680 mm、宽度B=505.71 mm、高度D=128.57 mm，模型长宽比约L/B=3.32；补偿段试验模型置于测力试验模型沿长度方向的前后两端，前段置于测力模型段来流端，后段置于测力模型段尾流端.斜风作用下时，考虑到补偿段模型长度可能对测力试验模型测试结果的影响，故分别选择了长度为2.4 m、1.2 m和0.48 m共3种补偿段试验模型，补偿段模型与测力试验模型几何外形完全一致.试验测试模型固定在试验支架上，该支架下侧与测力天平相连接；补偿段试验模型固定在测试试验模型两端外侧支架上.补偿段模型与测试试验模型之间间隙约为2 mm，置于风洞实验室中的补偿段试验模型和测力试验模型照片如图4所示.

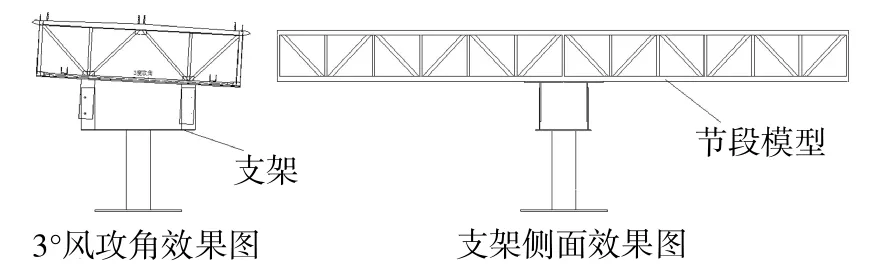
图3 试验支架示意图Fig.3 Test support frame diagram

首先针对桁架加劲梁成桥状态进行不同长度补偿段模型对测力试验模型结果的影响研究，以确定补偿段模型的合理长度，在此基础上再分别针对成桥状态和施工状态进行-3°～+3°风攻角、风偏角β为0°～90°（间隔为 5°）下板桁结合加劲梁气动力系数测试.具体试验工况见表1.

图4 不同补偿段试验模型照片Fig.4 Experimental model photos of compensation segments with different lengths

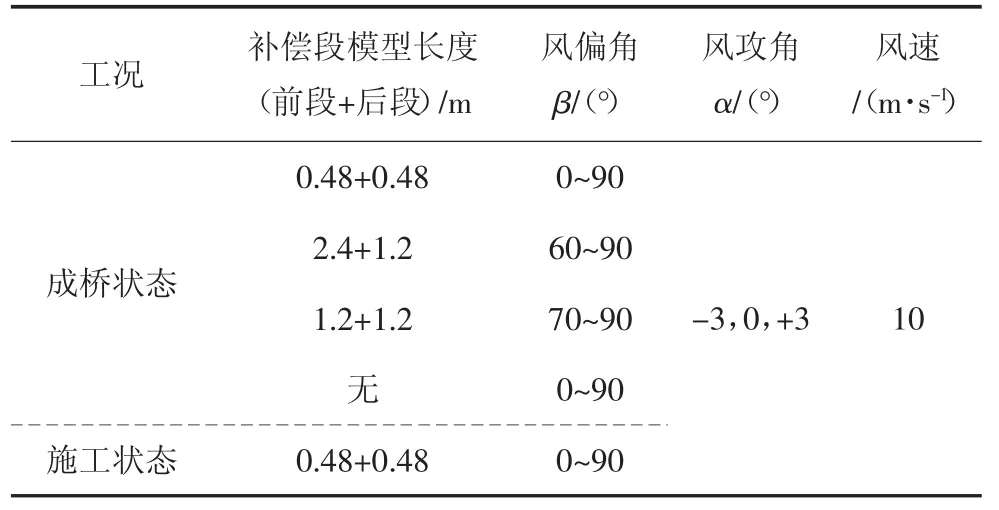
表1 岳阳洞庭湖二桥加劲梁气动力系数试验测试工况Tab.1 Test cases for static aerodynamic of the second bridge of Yueyang Dongting Lake

1.3 静气动力系数定义

图5为加劲梁静力四分力三维坐标系示意图，测力节段模型通过支架与测力天平连接.图5中α为风攻角，β为风偏角（风偏角对应风向垂直于桥轴线）.B、D和H分别为加劲梁节段模型宽度、高度和模型剪切中心到测力天平中心的距离.测力天平力系分别可由沿 x、y、z轴的力 Fx、Fy、Fz及绕 z轴的扭矩Mz表示.作用在加劲梁上的静气动力可以用体轴坐标系中的竖向升力FV、横桥向阻力FH、顺桥向阻力Ffr和绕主梁轴线方向的扭转力矩MT表示.

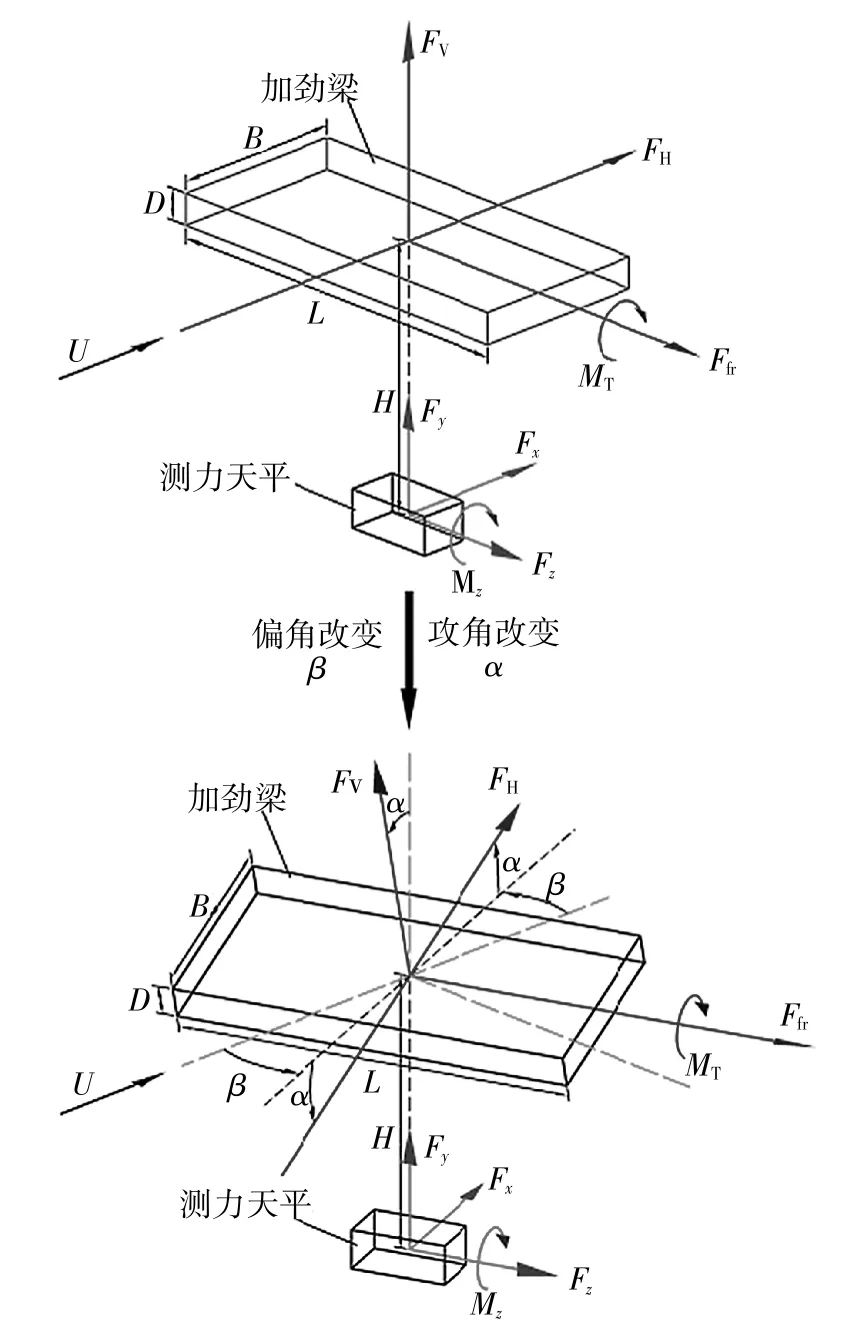
图5 加劲梁静气动力示意图Fig.5 Aerostatic forces of the stiffening girder

0°攻角工况下，测力天平x、y、z轴方向分别与测力模型横桥向、竖向和顺桥向一致.由于测力天平可与模型在水平面内同步转动改变偏角，而无法随模型攻角改变时在竖向平面内改变水平倾角，故在±3°攻角工况下，将测力天平力系对应的轴力在模型体轴系进行投影分解合成得到模型体轴力.

如图6所示，对应模型体轴坐标系气动力与测力天平坐标系力之间的关系如下式所示：

式中：α为风攻角；FH为加劲梁模型横桥向阻力；Ffr为加劲梁模型顺桥向阻力；FV为加劲梁模型竖向升力；MT为加劲梁模型绕桥轴线方向的力矩；Fx为测力天平x轴力；Fy为测力天平y轴力；Fz为测力天平z轴力；Mz为测力天平绕z轴的力矩；H为节段模型剪切中心到测力天平中心的高度.加劲梁体轴坐标系下四分力系数定义为：

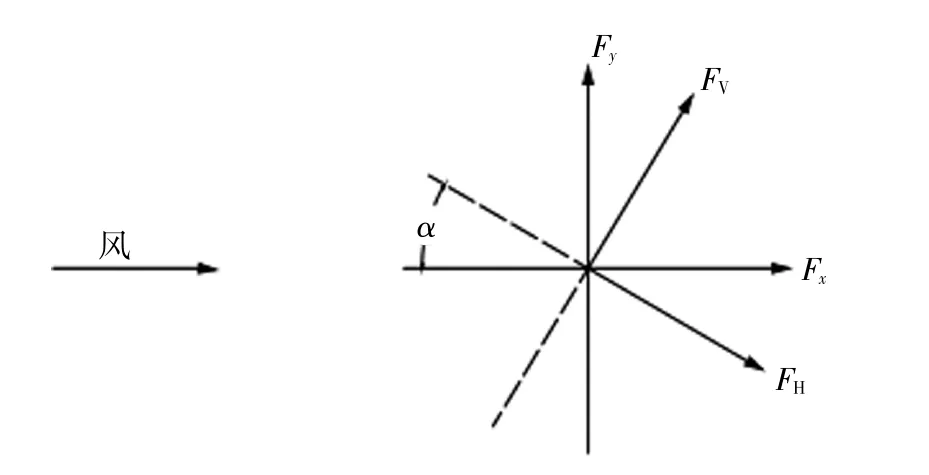
图6 加劲梁模型体轴力系与测力天平力系Fig.6 Coordinate systems for stiffening girder and force balance

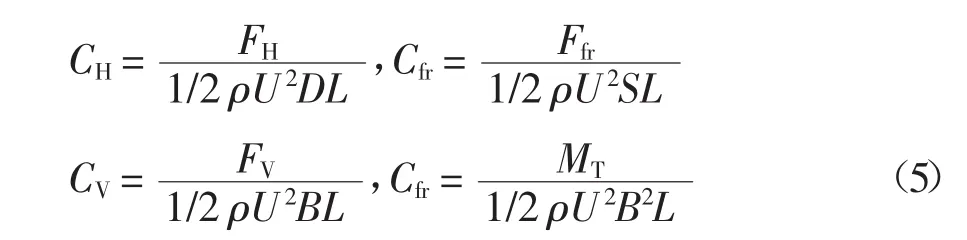
式中：CH为横桥向阻力系数；Cfr为顺桥向阻力系数；CV为竖向升力系数；CM为升力矩系数；U为试验风速；空气密度ρ=1.225 kg/m3；L、D、B和S分别为加劲梁测力节段模型的长度、高度、宽度和外轮廓周长.对于板桁结合加劲梁外轮廓周长S，计算方法为取加劲梁横断面最外围轮廓的长度，即如图7（桥面系未给出）所示加劲梁横断面外围粗实线的长度.

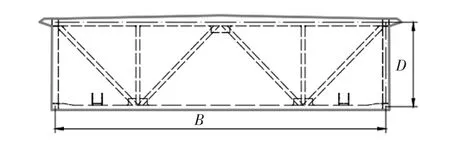
图7 加劲梁外轮廓周长示意图Fig.7 Outer contour perimeter of the stiffening girder

2 试验结果

2.1 补偿段模型长度影响

在进行斜风作用下加劲梁节段模型气动力系数测试时，考虑到桁架加劲梁测力模型的端部阻力效应和空间桁架干扰效应的影响，有必要进行不同长度补偿段模型对加劲梁节段模型气动力试验结果影响的研究.因此，针对成桥状态分别进行了0°、-3°和+3°风攻角时不同长度补偿段模型对应的测力试验.由于风洞试验场地宽度限制，补偿段模型长度分别为2.4 m+1.2 m、1.2 m+1.2 m时仅进行了风偏角为60°～90°时加劲梁气动力系数测试.图8～图11分别给出了不同风攻角下、不同长度补偿段模型对应的加劲梁气动力系数随风偏角变化曲线.

从图8～图11可见，增设补偿段工况与无补偿段工况的加劲梁模型测力试验结果差异较大，不同长度补偿段模型在同一风攻角工况下的测力试验结果差异总体较小.由图8可知，设置补偿段模型后板桁结合加劲梁横桥向阻力系数值总体小于不设置补偿段模型对应的加劲梁横桥向阻力系数值.相同长度补偿段对+3°风攻角时的CH值的影响比-3°风攻角时的较大，这是由于正风攻角工况下，补偿段模型桥面板下部的桁架结构对测力段模型前后气流扰动作用较大.如图9所示，风偏角β≥40°后，增设补偿段模型的顺桥向阻力系数Cfr明显小于无补偿段的试验结果，但是不同长度模型补偿段模型对板桁结合加劲梁Cfr的影响总体不大.由图10可见，桁架加劲梁竖向升力系数随风偏角的增加而先增加后减小；当风偏角为0°～20°时，补偿段模型对桁架加劲梁的竖向力系数影响随风攻角的变化而变化，当风偏角为20°～90°时补偿段模型对应的加劲梁竖向力系数较不设补偿段模型的结果小.从图11可知，不同风攻角下补偿段模型对桁架加劲梁升力矩系数的影响没有明显的规律，且其值较小.

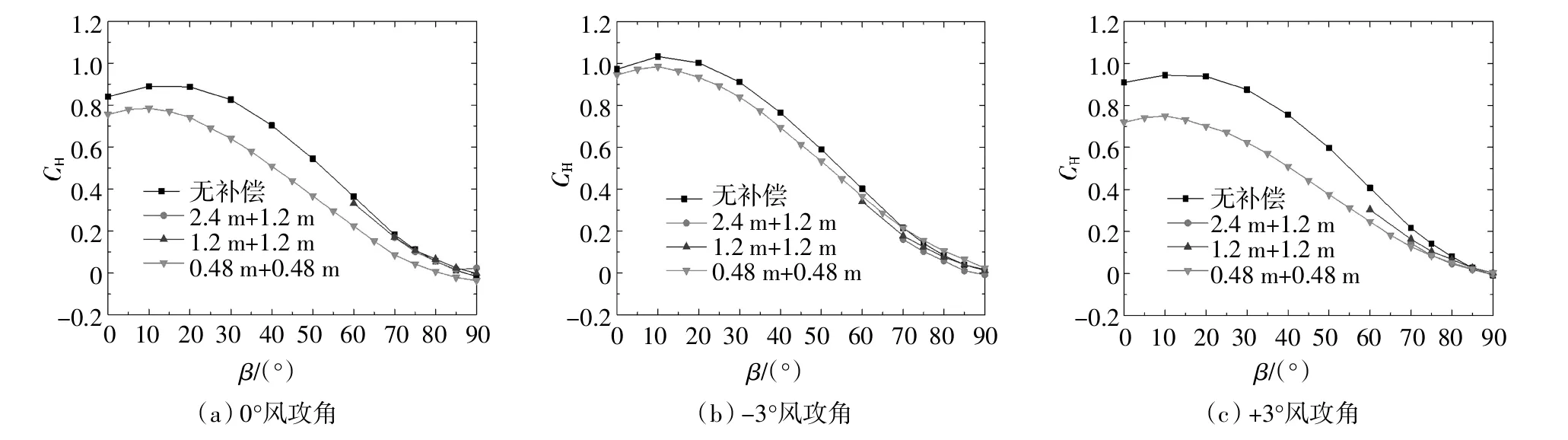
图8 不同长度补偿段模型加劲梁横桥向阻力系数Fig.8 Horizontal drag coefficients of the stiffening girder with different length compensation models

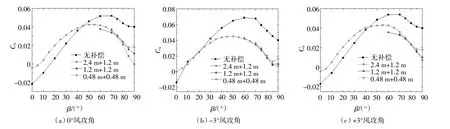
图9 不同长度补偿段模型加劲梁顺桥向阻力系数Fig.9 Longitudinal drag coefficients of the stiffening girder with different length compensation models

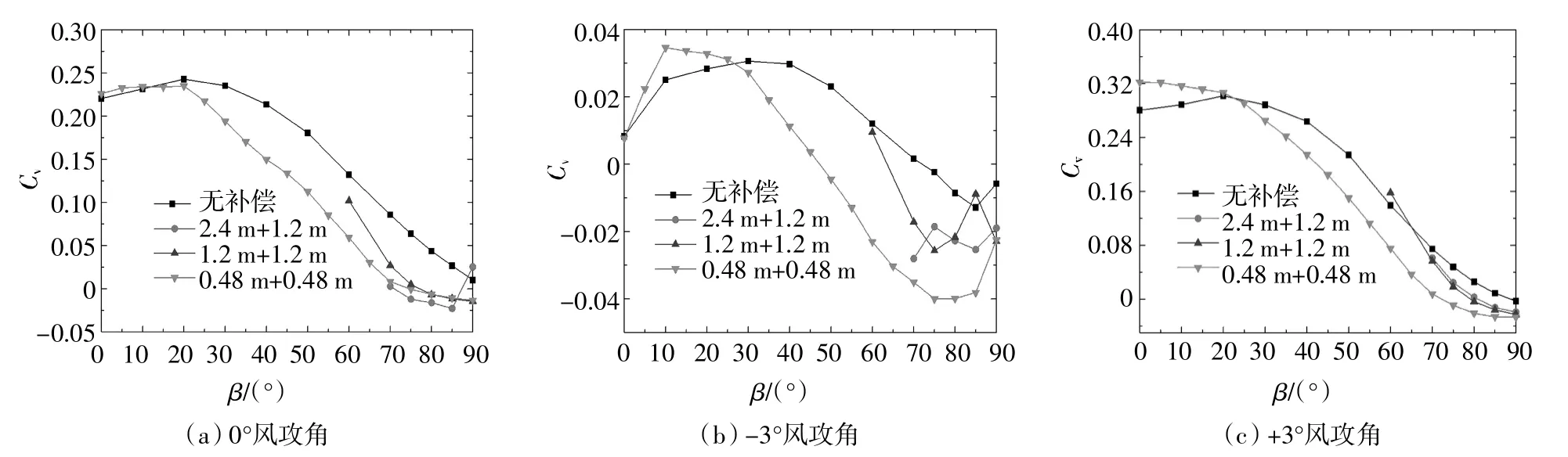
图10 不同长度补偿段模型加劲梁竖向升力系数Fig.10 Vertical lift coefficients of the stiffening girder with different length compensation models

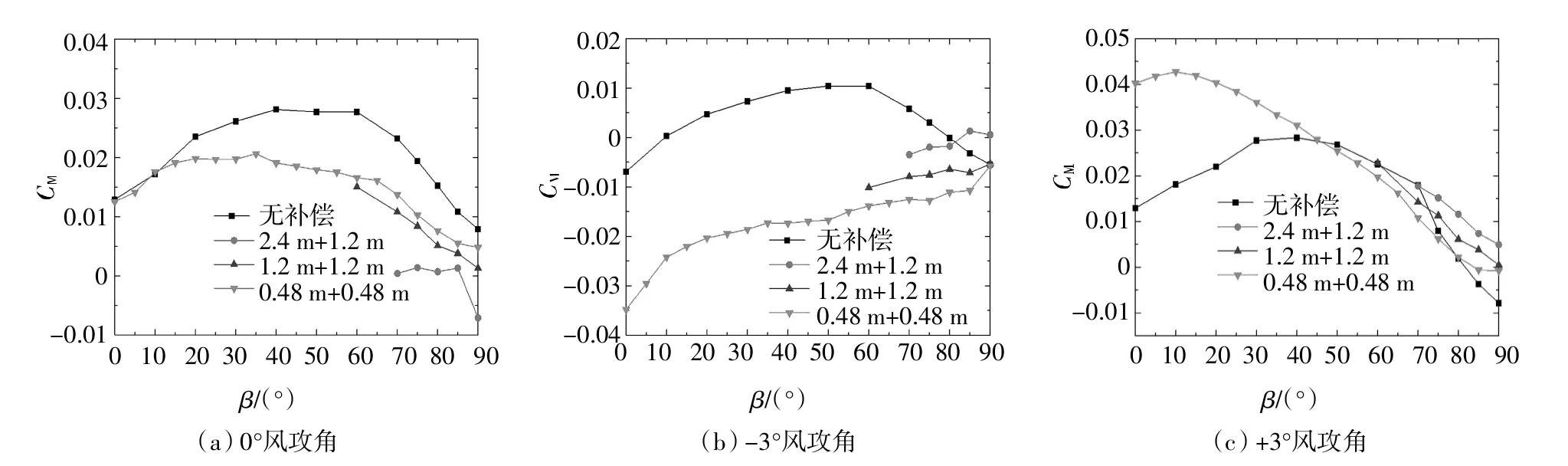
图11 不同长度补偿段模型加劲梁升力矩系数Fig.11 Pitch coefficients of the stiffening girder with different length compensation models

总体而言，进行板桁结合加劲梁气动力系数测试时设置一定长度的补偿段模型是必要的，一方面，考虑到风洞试验段宽度和风偏角测试范围，另一方面，对于结构设计偏安全考虑，本文综合确定选用长度为0.48 m的补偿段模型进行板桁结合加劲梁气动力系数试验研究.

2.2 静气动力系数试验结果

图12所示为不同风攻角下板桁结合加劲梁成桥状态和施工状态气动力系数随风偏角的变化曲线，各气动力系数最大值及其对应的风偏角如表2所示.

由图12（a）可知，板桁结合加劲梁横桥向阻力系数CH在风偏角为5°～10°时达到最大值，约为风偏角为0°时阻力系数值的1.05倍；同一风攻角工况下施工状态横桥向阻力系数小于成桥状态横桥向阻力系数值，两者之间的差值随风偏角的增加而减小；斜风作用下CH受攻角的影响较大，负风攻角的CH比正风攻角的数值大，加劲梁横桥向受力更加不利.由图12（b）可知，板桁结合加劲梁顺桥向阻力系数Cfr在风偏角为50°～55°时达到最大值；当风偏角为 90°（即顺桥向风）时，对应的顺桥向阻力系数Cfr约为其最大值的0.5倍；同一风攻角工况下，成桥状态顺桥向阻力系数值较施工状态顺桥向阻力系数值略大；在小风攻角（-3°～+3°）范围内，顺桥向阻力系数受风攻角的影响较小，各工况顺桥向阻力系数最大值相差不大.由图12（c）可知，板桁结合加劲梁竖向升力系数CV随风偏角的增加而逐渐减小，当风偏角为0°～20°时变化较小，当风偏角为20°～70°时减小较为明显，当风偏角为70°～90°时又逐渐趋于平缓.由图12（d）可知，板桁结合加劲梁升力矩系数绝对值随风偏角的增大而减小.

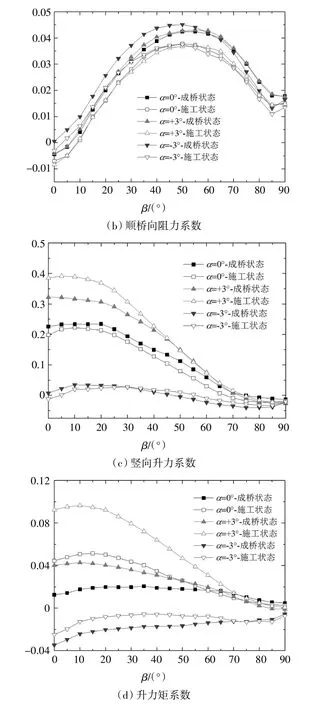
图12 成桥状态与施工状态静力四分力系数随风偏角变化曲线Fig.12 Static four-component coefficients under construction state and in-service state vs yaw angles

2.3 顺桥向阻力系数曲线拟合

为便于工程应用，分别对板桁结合加劲梁成桥状态和施工状态顺桥向阻力系数随风偏角变化的试验结果进行拟合，并确定板桁结合加劲梁顺桥向阻力系数的拟合公式为：

式中：Cfr（β）为风偏角为β时对应的桁架加劲梁顺桥向阻力系数；β为风偏角（°）；y0，A，k，b均为拟合系数.

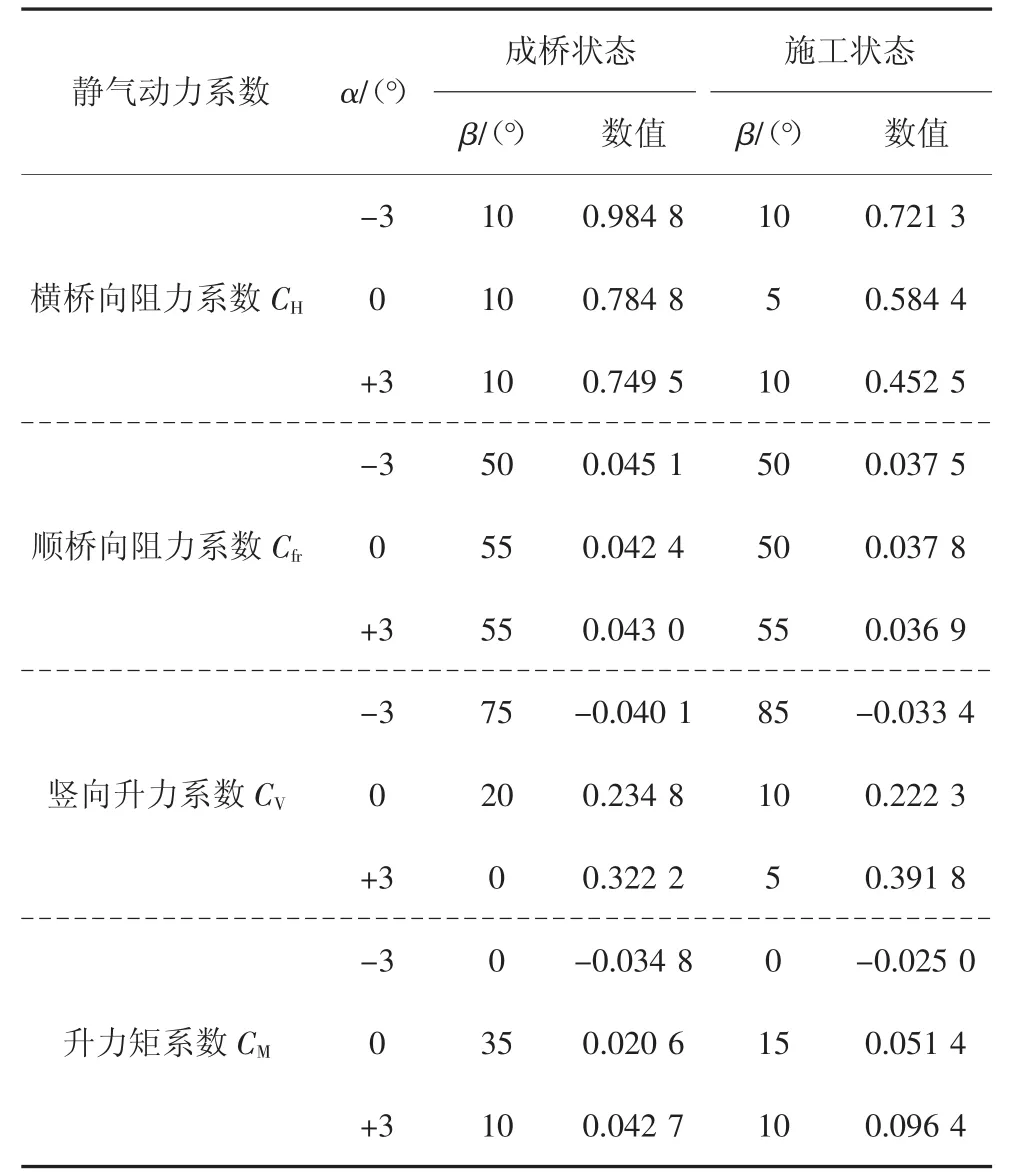
表2 板桁结合加劲梁气动力系数最大值及对应风偏角Tab.2 Maximum values of aerostatic coefficients of PTCSG and corresponding yaw angles

图13所示为-3°～+3°风攻角范围内板桁结合加劲梁成桥状态和施工状态顺桥向阻力系数随风偏角变化的试验结果及包络拟合曲线.式（7）（8）分别给出了桁架加劲梁成桥状态和施工状态顺桥向阻力系数随风偏角变化的拟合公式，即

成桥状态：

施工状态：

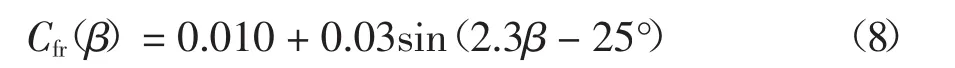
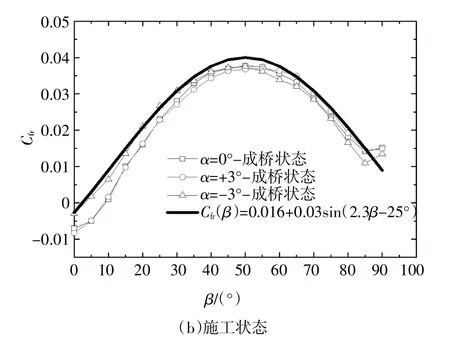
图13 板桁结合加劲梁顺桥向阻力系数拟合曲线Fig.13 Fitted curves of longitudinal drag coefficients of PTCSG vs yaw angles

2.4 试验结果与规范比较

我国《公路桥梁抗风设计规范》（JTG/T D60－01—2004）[16]中第4.3.6规定跨径小于200 m的桁架桥梁的顺桥向单位长度的风荷载取其横桥向风荷载的0.50倍，然而对跨径超过200 m的桁架桥梁的顺桥向风荷载并没有给出参考值，而不同风偏角下顺桥向的风荷载与横桥向单位长度风荷载之间并不是简单地呈一定的比例关系[14].欧洲EUROCODE 1规范[17]和英国BS5400规范[18]关于桁架桥梁顺桥向风荷载也仅规定取横桥向风荷载的0.50倍.文献 [19]介绍了日本桥梁抗风设计规范（Wind Resistant Design Standard for HSB（2001））对于桁架桥梁风荷载的计算公式为：

式中：PD表示作用在主梁上的风荷载；μ2为修正系数，当计算横桥向风荷载时μ2=1.55，计算顺桥向风荷载时μ2=1.25；U为风速；空气密度ρ=1.225 kg/m3；横桥向阻力系数CD由风洞试验得到，顺桥向阻力系数CD取横桥向阻力系数的0.6倍；An为主梁、扶手及护栏迎风面的投影面积，顺桥向时投影面积取法与横桥向一致.

日本桥梁抗风设计规范对于桁架桥梁顺桥向风荷载的计算，其实质为取其横桥向风荷载的0.48倍.为了便于比较，对洞庭湖二桥板桁结合加劲梁一个标准节段对应的风荷载进行计算，表3所示为采用不同规范所计算的桁架加劲梁顺桥向风荷载结果汇总.

表3 板桁结合加劲梁标准节段顺桥向风荷载规范计算值与试验值Tab.3 Calculated results by codes and experimental results of longitudinal wind loads of the standard segment of PTCSG

由表3可知，-3°～+3°风攻角下，各工况顺桥向风荷载最大试验值与其正交风作用下横桥向风荷载的比值为0.47～0.59；而各工况顺桥向风荷载最大试验值与正交风作用下最大横桥向风荷载（87.5U2）的比值为 0.44～0.47；0°和+3°风攻角工况下，采用规范[16-19]计算得到的顺桥向风荷载值均小于其试验最大值；最不利工况-3°风攻角下的顺桥向风荷载规范[16-19]取值与试验值吻合较好，结果偏安全.故对于顺桥向风荷载按照我国现行规范[16]取值，宜偏保守地取-3°～+3°风攻角范围内最不利横桥向风荷载的0.5倍.

-3°～ +3°风攻角范围内，采用中国规范[16]、欧洲规范[17]和日本桥梁抗风设计规范[19]计算得到的顺桥向风荷载最不利值与采用拟合公式（7）得到的计算值的相对误差分别为4.2%、4.2%和0.6%，试验数据拟合值与规范推荐值十分接近，且规范取值偏安全.

3 结论

以岳阳洞庭湖二桥为背景，对斜风作用下的板桁结合加劲梁静气动力系数进行了试验研究，得到了如下主要结论：

1）进行斜风作用下的板桁结合加劲梁静气动力系数风洞试验测试时，从试验条件和精度两个方面考虑，加劲梁测力模型前后端设置长度约为测力模型长度30%的补偿模型即可.

2）板桁结合加劲梁横桥向力系数随风偏角的增加先增大后减小，当风偏角为5°～10°时达到最大值，约为0°风偏角时横桥向力系数的1.05倍；板桁结合加劲梁顺桥向阻力系数随风偏角的增加先增大后减小，当风偏角为50°～55°时达到最大；小风攻角（-3°～+3°）范围内，攻角对顺桥向阻力系数最大值的影响较小.

3）在小范围风攻角（-3°～ +3°）内，拟合了板桁结合加劲梁成桥状态和施工状态顺桥向阻力系数随风偏角变化的表达式；采用该拟合公式所得到的板桁结合加劲梁顺桥向最不利风荷载约为正交风作用下最大横桥向风荷载的0.48，与中国、欧洲和日本桥梁抗风设计规范推荐值较为接近.