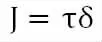基于D- M 模型的II 型加载裂纹问题的J 积分表达式

方豪

（重庆交通大学 土木工程学院，重庆400000）

1 概述

D-M模型是D.S.Dugdale 提出来的，他将如图1A 所示的曲线三角形看成裂纹的塑性区，并假设其区域内的材料具有理想塑性。[1]D-M模型是对贯穿裂纹的大型薄板拉伸试验的研究。本文想对D-M模型的裂纹加载方式进行改变，从I 型加载裂纹改为II 型加载经典裂纹，即让裂纹从受拉变为受剪。从而再来计算其J 积分的表达式。

2 COD 法及D-M 模型

COD 法又称裂纹张开位移法，这是由Wells 在1963 年提出的。[1]虽然这种方法是建立在实践之上的经验分析方法，但是工程界已经得到了广泛的应用。所谓COD，就是裂纹尖端的裂纹表面张开的位移量。这个位移量的大小很明显与对象的受载情况有关，两者是一一相关的，由此可得这个位移量的大小也同时对应裂纹端部一定的应力、应变场的强弱程度。对于金属材料尤其是延性较好的金属裂纹体，在荷载的作用下，由于裂纹尖端的应力集中的影响，该裂纹尖端材料会发生塑性滑移，这会导致裂纹尺寸的增大，裂纹尖端稍稍张开，从而引起裂纹尖端的钝化。[2]下文所用到的位移量δ，就是这里的COD 值，也是裂纹端部应力、应变场的间接度量。

但是COD 法仍然存在一些问题，比如COD 定义的究竟是裂纹上哪一点的位移量，目前也还没有统一的说法。

D-M模型实际如图1A 所示，其裂纹长度2c，计算所得强度因子为K1；而在图1B 中，同样是拉伸状态下的2a 长度的裂纹，所求得的强度因子为K1'；C 中在两个曲线三角形，也就是我们假设的理想塑性区单独加载所求得的强度因子为K1''。三者有如下关系：

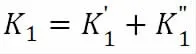
从上式可以得出A 可以拆分成B C 两个模型来分别计算，即A 模型是由B C 的叠加。

图1 D-M 模型示意图A（左）、B（中）和C（右）

3 公式推导

由于D-M模型是消除了奇点，如图2 所示的整个区域的应变都是小应变，所以J 积分的路线无关性是准确成立的。

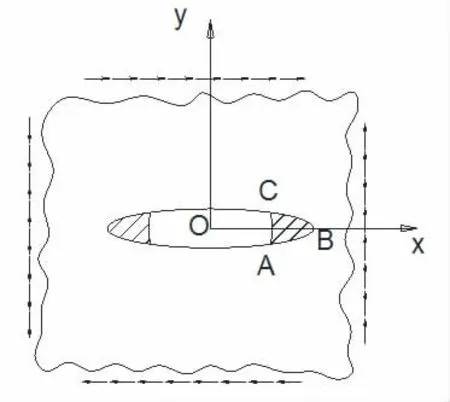
图2 积分示意图

这里选取弹塑性区域的边界线ABC 作为积分的回路来计算。J 积分有两种表达形式：一是回路积分定义的表达式；二是变形功率定义的表达式。其中回路积分定义为：[3]

其中：

dy=0

所以原式改成：

现有

带入(2)得：

设n1、n2为弧线元ds 的外法线方向n 的方向余弦，即：

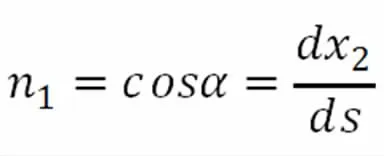
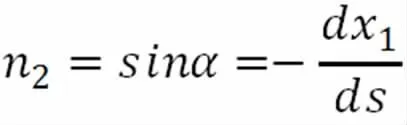
所以有：

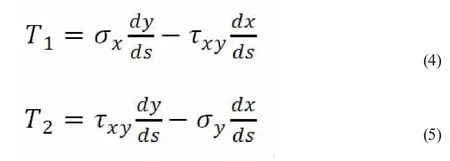
由于积分路线上有：

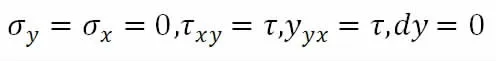
故：

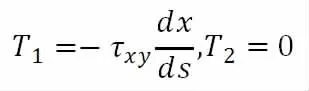
将其带入式(3)可得：

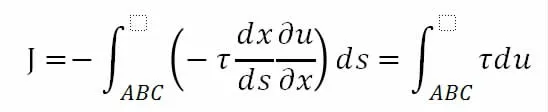
又因

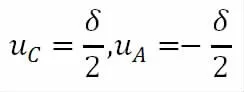
故得

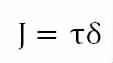
4 结论

推导得II 型裂纹下的J 积分表达式：