Mg2Ca相对镁合金形变和失效机理的影响
2020-06-03杜际广
杨 旗,杜际广,蒋 刚,3
(1.四川大学原子与分子物理研究所, 成都 610065;2.四川大学物理学院, 成都 610065;3.四川大学高能量密度物理与技术重点实验室, 成都 610065)
1 引 言
高性能结构材料中,镁及其合金在现有金属中有“最轻的工程材料”的美誉[1-2]. 但镁等密排六方(HCP)晶体的金属材料,结构上各向异性导致塑性成形性和延展性差、容易被腐蚀. 为了提高其成形性和耐腐蚀性,添加锂(Li)、铝(Al)、钙(Ca)、锌(Zn)、锆(Zr)和稀土(RE)等合金元素是目前最有效的方式之一[3]. 其中钙元素是自然界含量第三的金属元素,其价格相比稀土元素等低廉,故镁钙合金大量应用于汽车和航空航天等工业领域. 因此,多角度认识Mg-Ca合金的形变和失效机理是十分必要的. 这也可以帮助改进多组分的Mg-Ca-X(-X)合金. 在理想的条件下,钙在镁合金中的最大固溶度约为1.34 wt%[4],Mg2Ca沉淀物是唯一的稳定第二相[5-6]. 相较于全面研究了固溶Al原子和Mg17Al12沉淀物对合金性能影响的Mg-Al体系[7-8], Mg-Ca体系目前只讨论了固溶Ca原子的影响. 2015年,Reddy和Groh[9]模拟分析了固溶钙原子和温度对纯镁纳米晶体屈服面上的机械行为的影响. 2018年,Nahhas和Groh研究了纯镁和二元MgX合金(X=固溶原子Ca、Gd、Li、Sn、Y、Ag、Nd和Pb)中对称倾斜晶界结构、能量和强度[10]. 而涉及Mg2Ca沉淀的研究主要在实验或第一性原理计算方面,揭示的是其晶格结构、电子性质和热力学性质等[6,11-12], 尚不清楚Mg2Ca沉淀物的机械行为和其对Mg-Ca合金形变、破坏机理的影响. 综上所述,本文采用分子动力学方法,研究对比了Mg、Mg2Ca单晶体的机械性质和行为. 进一步分析多晶Mg/Mg2Ca复合材料模型的结构变化,揭示了Mg2Ca稳定相对镁合金形变和失效机理的影响.
2 模拟细节
本文分子动力学模拟使用LAMMPS软件[13],数据用OVITO软件进行可视化分析[14]. 最新2NN-MEAM势函数用来描述Mg、Ca原子间相互作用[15]. 如表1成功复现了Mg和Mg2Ca单晶的弹性常数. Mg、Mg2Ca的实验值(Exp)分别来自文献[16-17],其它计算值(Cal)来自文献[18-19].

表1 单晶Mg、Mg2Ca弹性常数当前计算值(2NN)、实验值(Exp)和其他计算值(Cal)
Tab.1 Elastic constants of Mg and Mg2Ca, the present (2NN) and experiment (Exp) and others (Cal)

弹性常数/GPaMg Mg2Ca2NNExpCal2NNExpCal C1162.8963.560.565.1861.259.5 C1226.2925.926.120.1417.617.8C1321.2621.722.319.2015.012.6C3369.9566.573.158.2265.566.0C4417.2218.413.421.7219.317.4C6618.3018.817.222.5221.820.9

图1 纯Mg单晶体和多晶Mg/Mg2Ca复合材料初始模型Fig.1 Initial model of Mg/Mg2Ca nanocomposite and Mg single-crystal

ES 引擎的索引机制基于倒排索引(Inverted Index)技术开发,文档的关键词来组成文档集合。在用户搜索时,首先将搜索词与关键词文档集进行匹配,再根据各文档在该关键词集的权重量来对搜索结果排序。但是,由于ES 搜索核心的分词表默认为英语,对中文文档的分词和归类能力比较薄弱;同时,在文档的权重计算上,也没有考虑到域内用户的检索偏好,在搜索结果的相关度上与用户实际要搜索的内容匹配度不高。针对以上两个ES 系统的缺陷,本文针对性地对分词技术和文档权重计算算法进行了优化,进一步提升校内用户的搜索体验。
3 结果与讨论
3.1 单晶Mg、Mg2Ca机械性能
图2为单轴拉伸载荷下Mg、Mg2Ca单晶体应力-应变曲线. 初始时应力随应变直线增加,表明模型处于弹性阶段. 斜率值表示杨氏模量,明显的Mg2Ca值大即其刚度也大. 峰值应力近似为屈服应力,对应的应变为屈服应变. Mg2Ca屈服应力大于Mg,但屈服应变小.

图2 单轴拉伸载荷下单晶体Mg、Mg2Ca应力-应变曲线Fig.2 The stress-strain curves of single-crystal Mg and Mg2Ca under uniaxial tensile loading

图3 单轴拉伸载荷下单晶体Mg、Mg2Ca原子构型(ε-应变)Fig.3 Atomic structure of single-crystal Mg and Mg2Ca under uniaxial tensile loading (ε-strain)


图4 单轴剪切载荷下单晶体Mg、Mg2Ca应力-应变曲线.Fig.4 The stress-strain curves of single-crystal Mg and Mg2Ca under uniaxial shear loading.

3.2 多晶Mg/Mg2Ca复合材料机械行为
图6为拉伸载荷下纯镁和应变0.075、0.125时多晶Mg/Mg2Ca(a)表面、(b)X-Y截面的原子构型. 从晶体表面来看,相比纯镁,复合材料易从Mg/Mg2Ca晶界处断裂. 晶体内部,从图6(b1)可以发现,裂缝产生于Mg基体和Mg2Ca颗粒的三重连结处,从而使区域应力降低. 在相邻的Mg/Mg晶界裂缝尖端处应力集中,使裂缝沿晶界扩展,导致材料断裂. 图6(b2)可观察到材料右下方Mg基体微形变,但对于材料失效机理影响可忽略.
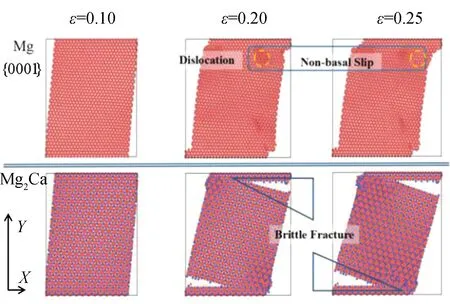
图5 单轴剪切载荷下单晶体Mg、Mg2Ca原子构型Fig.5 Atomic structure of single-crystal Mg and Mg2Ca under uniaxial shear loading

图6 单轴拉伸载荷下多晶纯镁与Mg/ Mg2Ca复合材料原子构型, (a)为完整结构,(b)为X-Y截面结构,其中方框区域显示原子应力分布Fig. 6 Atomic structure of pure Mg and Mg/Mg2Ca nanocomposite under uniaxial tensile loading, (a) presents whole model, (b) presents X-Y cross-sectional structure, the frame represents the atomic stress field
图7为单轴剪切荷载作用下纯镁和应变0.150、0.400时多晶Mg/Mg2Ca(a)表面、(b)X-Y截面原子构型. 剪切过程的应力分布明显不均. 如图7(b1)所示,在晶体内部的Mg/Mg晶界应力高度集中,促使晶界形成基面和非基面
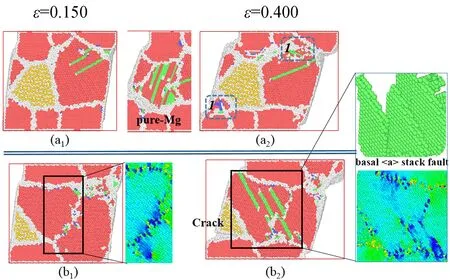
图7 单轴剪切载荷下多晶纯镁与Mg/ Mg2Ca复合材料原子构型(与图 6类似)Fig.7 Atomic structure of pure Mg and Mg/Mg2Ca nanocom-posite under uniaxial tensile loading (similar to Fig.6)
4 结 论
本文采用MD方法,利用最新2NN-MEAM势函数研究了Mg、Mg2Ca单晶的机械行为,对比揭示稳定相Mg2Ca对多晶Mg-Ca合金机械行为的影响. 在负载形变中,Mg2Ca颗粒的几何构型都保持不变,减少和阻断位错等缺陷,锚定了周围原子. 使合金具有抗蠕变优势. 但同时较弱Mg/Mg2Ca界面易产生的晶间裂缝增强了脆性,促使材料失效. 这与金属形变Orowan机理所揭示的第二相的作用相似. 另外,对比单晶与多晶体的结果,可以发现Mg塑性形变中基面位错相比锥面
