钢波纹板混凝土拱加固体系有限元分析*

宋福春， 王厚宇， 赵 洁， 张冠华

(1. 沈阳建筑大学 交通工程学院， 沈阳 110168； 2. 辽宁省交通规划设计院有限责任公司 公路养护技术研发中心， 沈阳 110111)

由于我国早期设计的桥梁，设计标准普遍偏低，伴随着国家交通的高速发展以及荷载等级的提高，部分旧桥已经出现了不同程度的病害，对于旧桥加固的研究势在必行[1-2].钢波纹板的出现与发展，为旧桥加固提供了新的可能[3].所谓钢波纹板，即平面钢板按照规定的规格尺寸利用机械模压等加工出波纹，在断面形成波状的钢板产品[4-5].根据现场的组装形式可分为波纹圆管(分节组装)和波纹钢板(分片拼装)两种[6-7].钢波纹板通过褶皱效应，使较薄的钢板拥有较大的截面惯性矩，能够很好地参与受力.但钢板较薄，易发生局部失稳现象，且与桥墩、桥台不宜连接.通过钢波纹板与混凝土的组合能够实现优势互补，形成易于施工，安全储备大的加固体系，适用于现代桥梁的加固[8-10].

本文利用有限元软件，建立空间有限元模型进行模拟钢波纹板与混凝土的实际受力情况，分析钢波纹板加固体系的特性，解决传统内力计算无法处理的问题.为桥梁加固工程的设计、施工和科研提供建议和参考.

1 依托工程

依托工程位于京哈高速段某空心板桥梁.该桥分为左右两幅，全长18 m，跨径布置为1×10 m，桥面净宽2×15 m.该桥上部结构为预应力混凝土空心板，左、右两幅各16块板，下部结构为钢筋混凝土薄壁台，采用桩基础，交角为117°，设计荷载为汽超-20、挂-120.因高速公路交通量不断增大，过往的重载车辆日益增多，该桥已出现严重的病害.

2 加固方案

根据桥梁的病害情况，采用新浇筑台身设置拱形钢波纹板抢修方案.具体加固方法为：在原桥顶面浇筑混凝土桥台，桥面下方，布置一道拱形钢波纹板，板片拱脚与新建桥台上预埋的角钢螺栓连接，然后在与桥面的空隙中填充C25自密实微膨胀小石子混凝土，使波纹板拱代替原有构件成为主要受力结构.

3 钢波纹板加固模型有限元分析

3.1 模型创建

图2 拱上混凝土Fig.2 Arch concrete

图3 空心板及编号Fig.3 Hollow plate and numbering

3.2 单元类型及参数选取

选取Shell63四节点壳单元建立钢波纹板拱.拱上混凝土选取Solid95二十节点实体结构单元建立.空心板梁同样选取Solid95单元.钢波纹板和拱上新浇筑的混凝土之间采用接触单元Con-tal74和Targel70模拟[12].

由于原桥空心板在7#、9#、10#、12#和13#存在较大裂缝，几乎丧失承载能力，安全起见，有限元模拟时取其弹性模量为1 GPa，接近于原混凝土的1/30.相关材料参数如表1所示.

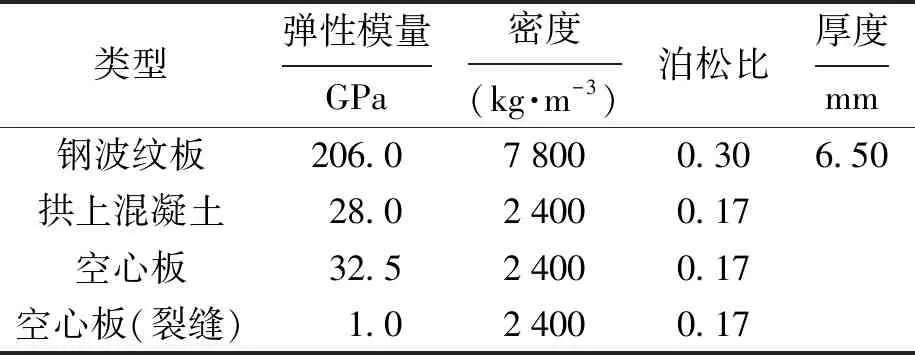
表1 钢波纹板体系材料参数Tab.1 Material parameters for steel corrugated plate system

3.3 网格划分与边界条件

3.3.1 网格划分

钢波纹板的单元形状取四边形，实体单元取六面体，依次对钢波纹板单元、拱上填筑混凝土单元、原桥空心板混凝土单元进行网格划分，将全桥划分为473 527个节点，300 720个单元.钢板和混凝土之间采用接触单元实现连接，如图4所示.

图4 有限元网络Fig.4 Finite element meshing

3.3.2 边界条件

拱底钢波纹板约束所有位移和扭转自由度，施加ALL DOF约束.拱上混凝土拱底截面上所有节点约束所有位移自由度UX、UY和UZ，空心板梁端节点约束竖向位移UY，横桥向水平无位移约束.

4 有限元分析结果

4.1 恒载作用下钢波纹板体系特性分析

4.1.1 恒载作用下变形分析

自重作用下，最大竖向位移发生在空心板边板跨中，最大值为1.93 mm.钢波纹板拱刚度较大，竖向变形最大值位于跨中拱的两端，为0.214 mm，竖向位移图如图5所示.

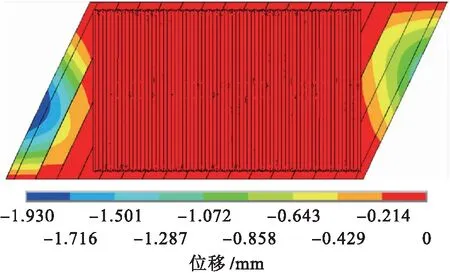
图5 自重作用下竖向位移图Fig.5 Vertical displacement diagram under self-gravity

由图5可知，自重荷载作用下原桥空心板边板位移最大.拱形钢波纹板整体向下挠曲，拱顶竖向变形最大，但较空心板边板小一个数量级，因此，柔性结构的拱形钢波纹板与拱上混凝土形成一个整体结构，总体变形比较小.

社会发展是教育变革和教育发展的源动力。不久前，我国提出提升中国国力进而繁荣全球的“一带一路”倡议，教育变革无疑要呼应国家这一宏伟战略决策。也就是说，当代教育不可仅满足于对学生的单一专业能力的有限培养，更需要关注学生通晓国际文化、具备国际意识与视野的培养，需要使他们在具备专业知识的同时，掌握敏锐洞察、有效沟通、解决国际问题的能力、持续保持国际先进水平并不断更新知识的能力。总之，当代“人工智能+教育”的人才培养目标定位，必须是突破专业技能和一般性交际能力界域，国际视野和全球化实战能力兼具的综合人才。

4.1.2 恒载作用下内力分析

恒载作用下，结构体系中钢波纹板第一主应力、第二主应力和第三主应力如图6～8所示.

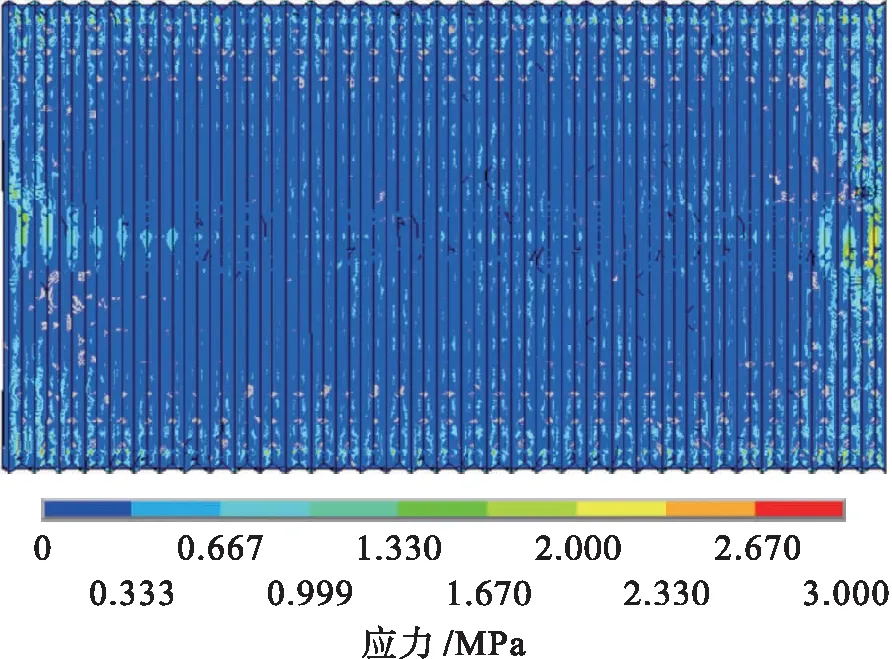
图6 恒载作用下钢波纹板第一主应力图Fig.6 First principal stress diagram of steel corrugated plate under constant load

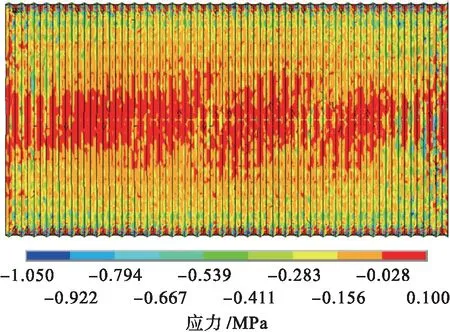
图7 恒载作用下钢波纹板第二主应力图Fig.7 Second principal stress diagram of steel corrugated plate under constant load

图8 恒载作用下钢波纹板第三主应力图Fig.8 Third principal stress diagram of steel corrugated plate under constant load

分析可知，在恒载作用下，拱顶主应力绝对值明显大于1/4跨和拱脚附近区域，钢波纹板拱顶以受拉为主，拱脚以受压为主.钢波纹板桥梁在竖直方向大致是应力依次增大，而在水平方向离钢波纹板拱越近则应力越大，越远则应力越小.在拱脚和拱顶的变形较大，产生的应力也较大.

4.2 恒、活载共同作用下钢波纹板体系特性分析

设置参数与上述恒载作用下保持一致，不考虑活载移动产生的冲击力.加载方式为先在跨度范围内施加均布荷载，然后再考虑集中力从跨边依次移动到跨中，分析活载作用下钢波纹板桥梁受力情况.

4.2.1 汽车荷载作用下内力分析

汽车荷载通过拱上填料传递到钢波纹板桥上，活载随着钢波纹板桥涵上填料厚度的改变而变化，即在填料厚度最小时活载占总荷载的比例最大，随着拱上填料厚度的增加，活载所占比例逐渐减少.汽超-20荷载作用下，结构体系中钢波纹板第一主应力、第二主应力和第三主应力如图9～11所示.

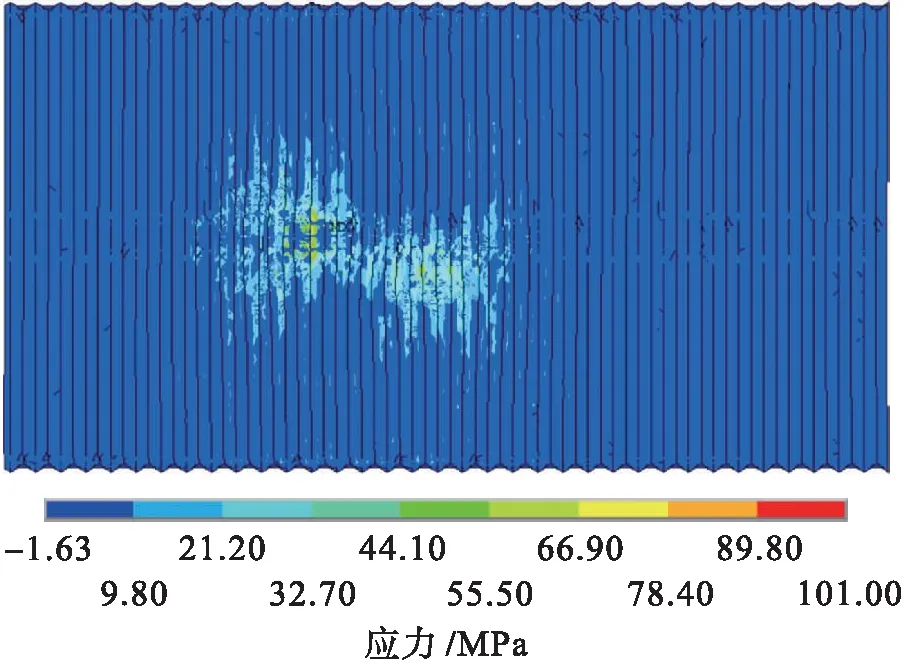
图9 汽超-20荷载作用下钢波纹板第一主应力图Fig.9 First principal stress diagram of steel corrugated plate under steam super-20 load

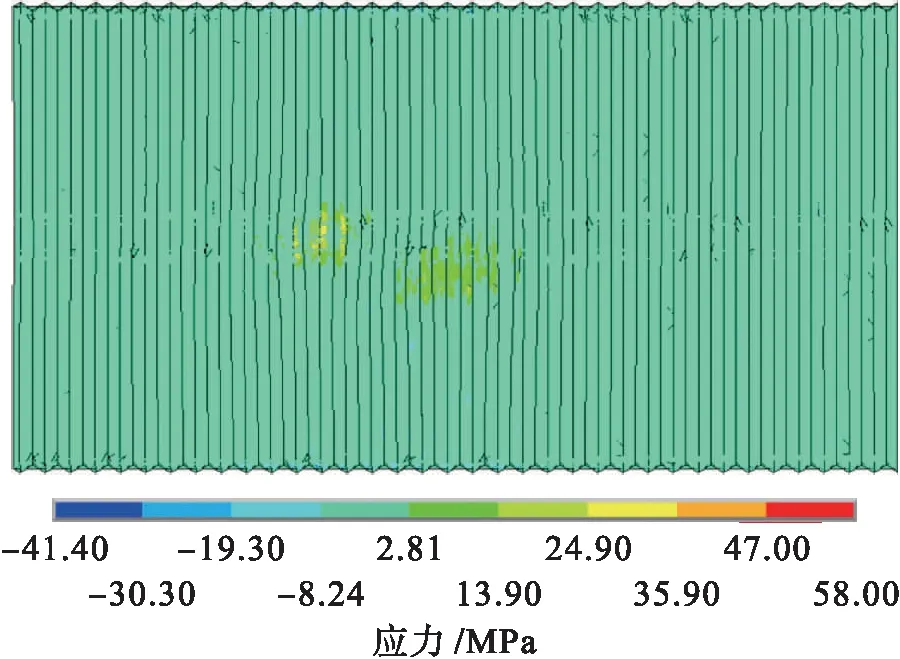
图10 汽超-20荷载作用下钢波纹板第二主应力图Fig.10 Second principal stress diagram of steel corrugated

在汽车荷载作用下，加固结构体系产生较大内力，钢波纹板第一主应力最大值达66.9 MPa，为拉应力，位于拱顶.第二主应力和第三主应力的空间分布与恒载作用下相似，但数值增加明显.钢波纹板受力较为均匀，第一主应力位于拱顶靠近跨中区域，取得最大值.拱顶第一主应力明显大于1/4跨和拱脚附近区域，但是拱顶大部分区域受压，在断板区域受力明显为拉应力.而拱顶区域的第三主应力小于1/4跨和拱脚附近区域，拱脚处第三主应力最大值为68.4 MPa.

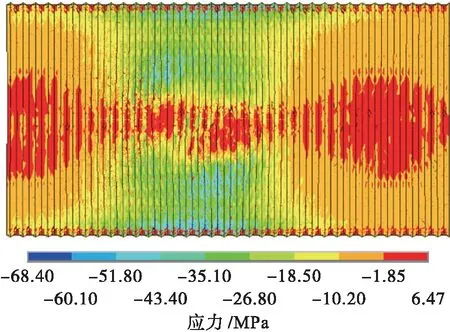
图11 汽超-20荷载作用下钢波纹板第三主应力图Fig.11 Third principal stress diagram of steel corrugated

由于挂车荷载采取中间车道加载，由图12可以看到，拱顶中间位置竖向变形最大且比较集中，最大竖向变形值为1.75 mm.其整体变形相对较小，反映出钢波纹板混凝土加固拱整体刚度较大，具有较充裕的安全储备.

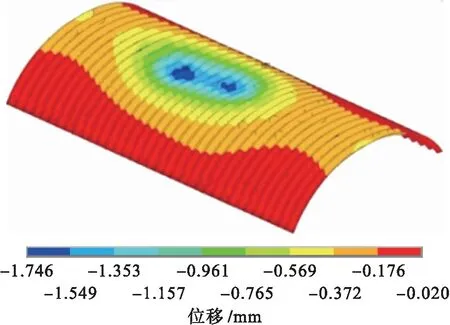
图12 挂车荷载作用下钢波纹板竖向位移图Fig.12 Vertical displacement diagram of steel corrugated plate under trailer load

4.2.3 挂车荷载作用下内力分析

挂-120荷载作用下，结构体系中钢波纹板第一主应力、第二主应力和第三主应力如图13～15所示.可以看出，在挂车荷载作用下，加固结构体系产生较大内力，主要集中在加载车道下方，第一主应力最大值达到67.9 MPa，为拉应力，与汽超-20荷载内力值较接近.第二主应力和第三主应力的空间分布与汽超-20荷载作用下相似.拱顶区域的第三主应力小于1/4跨和拱脚附近区域，拱脚处第三主应力最大值为76 MPa，稍大于汽超-20荷载的第三主应力值.1/4跨和拱脚附近区域第三主应力主要处于21.0～57.6 MPa之间，稍小于汽超-20荷载的拱脚区域的第三主应力，这表明汽车荷载作用时，钢波纹板拱受力更加均匀，而挂车荷载作用下，结构体系存在一定的应力集中.

图13 挂车荷载作用下钢波纹板第一主应力图Fig.13 First principal stress diagram of steel corrugated plate under trailer load

图14 挂车荷载作用下钢波纹板第二主应力图Fig.14 Second principal stress diagram of steel corrugated plate under trailer load

4.3 恒载参数变化下钢波纹板体系特性分析

为了与钢波纹板体系在恒载作用下的内力和变形情况进行对比，在原有275 mm填筑混凝土厚度的基础上，考虑拱顶混凝土厚度分别为175、275、375、475和575 mm，共五种填筑高度下的内力和变形趋势，选取挂-120荷载作用.

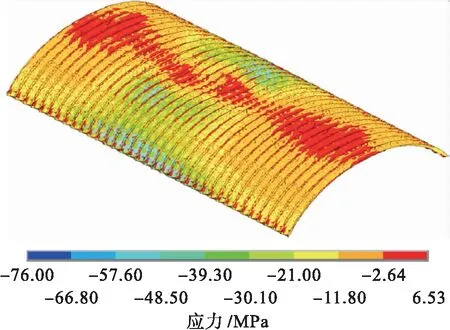
图15 挂车荷载作用下钢波纹板第三主应力图Fig.15 Third principal stress diagram of steel corrugated plate under trailer load

4.3.1 恒载参数变化对钢波纹板体系的变形影响

在其他条件不变的情况下，钢波纹板拱上混凝土填料逐级增加，填料厚度与钢波纹板拱顶竖向最大位移关系如图16所示.回填混凝土的竖向最大位移与钢波纹板拱竖向最大位移随着拱顶混凝土高度的增加而减小，且两者大致呈线性关系.

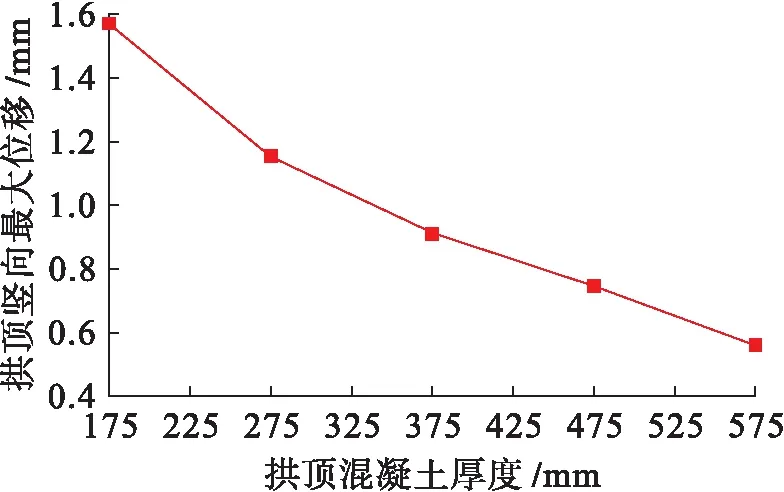
图16 填料厚度与钢波纹板拱顶竖向最大位移关系

Fig.16 Relationship of maximum vertical displacement between filler thickness and arch top of steel corrugated plate

4.3.2 恒载参数变化对钢波纹板体系的内力影响

在钢波纹板拱顶混凝土厚度增加后，钢波纹板的单元最大内力变化如图17所示.

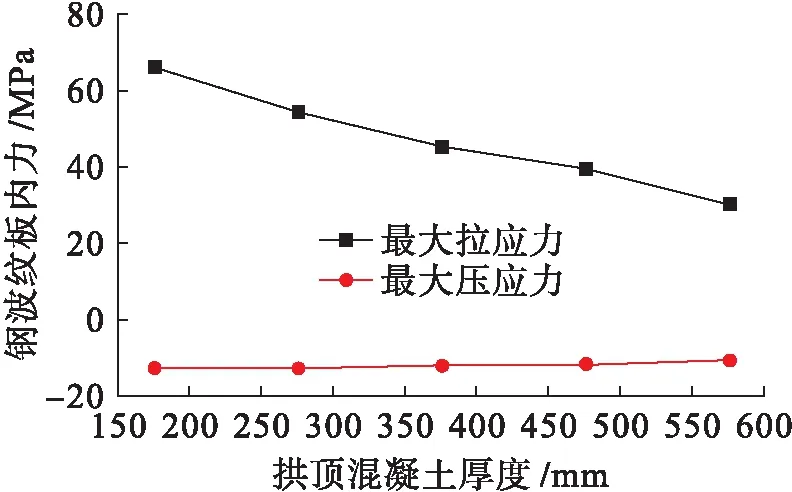
图17 填料厚度与钢波纹板拱内力关系Fig.17 Internal force relationship between filler thickness and steel corrugated plate arch

随着钢波纹板拱顶混凝土厚度的增加，最大应力(受压)和最小应力(受拉)均相应减小.因增加钢波纹板拱顶混凝土填料厚度时，所受压应力减小较快，故其最大压应力减小更快.

图18、19分别为175和575 mm厚钢波纹板拱上混凝土填料弹性应变图.通过对比可知，随着混凝土填料高度的增加，钢波纹板拱的弹性应变也相应减小.随着拱顶混凝土填料厚度增高，钢波纹板拱与混凝土填料相互作用而产生的弹性应变影响范围逐渐缩小.当混凝土填料高度减小到一定程度后，钢波纹板和混凝土回填料相互作用产生的应变一直扩大到拱顶混凝土的表面.

图18 175 mm厚混凝土填料弹性应变图Fig.18 Elastic strain diagram of concrete filler with thickness of 175 mm

图19 575 mm厚混凝土填料弹性应变图Fig.19 Elastic strain diagram of concrete filler with thickness of 575 mm

表2为混凝土填筑厚度与混凝土应力之间的关系.由表2可以看出，关键界面(拱顶截面)的最大拉应力在混凝土填料厚度为175 mm时，最大拉应力为1.54 MPa，钢波纹板拱上混凝土所受绝对值最大拉应力较为突出，大于C25混凝土轴心抗拉强度设计值ft=1.27 N/mm2.

表2 混凝土填筑厚度与混凝土应力之间的关系Tab.2 Relationship between concrete filler thickness and concrete stress

表2中，最大应力和最小应力均取绝对值.其中，混凝土受压为负值，受拉为正值；最大拉应力在拱顶位置和压应力的拱脚位置.最大拉应力点在钢波纹板拱的拱顶位置，所以当钢波纹板拱顶混凝土填筑厚度进一步减小时，对于拱顶等部位所受拉应力较大的地方混凝土受拉会产生裂缝，故应保证拱顶混凝土厚度在275 mm以上，确保结构的安全.

5 结 论

本文主要依据有限元结构软件来分析钢波纹板混凝土拱桥梁加固体系的结构受力和变形等特性，并得出以下结论：

1) 分析钢波纹混凝土拱加固体系在各类荷载作用下位移情况得出，体系在拱顶处位移最大，在最不利情况下，最大竖向位移也在拱顶处.

3) 通过对比汽车荷载和挂车荷载得知，钢波纹板拱加固体系在汽车荷载作用下受力更加均匀，而在挂车荷载作用下，结构体系存在一定的应力集中.

4) 通过钢波纹板加固结构体系拱顶混凝土厚度的参数分析可知，随着拱顶混凝土填筑厚度的增加，钢波纹板的应力应变逐渐减小，拱上结构的联合作用增大，上部荷载的传递更为均匀.同时，钢波纹板拱顶混凝土填筑厚度的保守范围应在275 mm以上，才能满足结构受力要求.

5) 钢波纹板结构具有较好的物理、力学性能，具有强度高、延性好的特点，适用于复杂地基，应用于空心板旧桥加固工程，有着广泛的使用前景.