基于神经网络预测ORC系统的最佳蒸发温度

陈 薇 袁中原

基于神经网络预测ORC系统的最佳蒸发温度

陈 薇 袁中原

（西南交通大学机械工程学院 成都 610031）

有机朗肯循环系统（ORC）的蒸发温度是决定系统净发电量的关键参数。采用热力学的方法建立数值模型，计算了不同热源温度、冷凝温度及蒸发器夹点温差下的最佳蒸发温度。以此为样本，对神经网络模型进行训练，研究神经网络对ORC系统最佳蒸发温度的预测效果。结果表明，训练速率为0.4、隐层神经元数目为5、训练函数为“trainlm”时，神经网络的预测精度最高。采用两种方式对神经网络的预测结果进行验证，具体为：（1）以9:1比例划分训练集和验证集，（2）系统输入参数取值范围内随机生成100组数据作为验证集。两种验证方式的结果均显示，神经网络对ORC蒸发温度的预测值与数值模拟值较为接近，误差均在2%范围内，表明神经网络模型可以较好的预测ORC最佳蒸发温度，可以为ORC系统的运行参数优化提供参考。

有机朗肯循环；余热发电；最佳蒸发温度；神经网络

0 引言

在煤化工和石化等行业中，通常需要将温度范围在60～200℃之内的低温工艺流体冷却到工艺要求的目标温度。目前工业上采用的常规冷却方式大多为水冷和空冷，冷却过程中需要消耗大量能量，且浪费了低温流体的热量[1-5]。研究者们进行了大量的研究表明有机朗肯循环（ORC）在低温余热发电方面有很大的潜力[6-10]。

有机朗肯循环系统的运行参数优化，可以较好的提高系统的发电效率。张军辉[11]等人采用全局寻优的方式，分析了10种不同工质在亚临界状态下的特性。结果表明，每种工质均存在一最佳蒸发温度使循环净输出功最大。于浩水[12]选择了R245fa作为有机工质，采用全局寻优数值仿真及实验验证的研究方法，研究了热源质量流量、温度、环境温度对系统的对外输出功、热效率、火用损失的影响，表明存在最佳热源温度和环境温度使得系统的火用效率和对外输出功达到最大。贺超[13]研究了在亚临界工况和超临界工况下的蒸发压力、膨胀机进口温度、冷凝温度对热效率、净输出功、火用效率的影响，建立包含热力学指标和热经济性指标的综合指标。严家禄[14]通过理论分析的方法，推导得出了两种不同热源下的最佳蒸发温度和最佳冷凝温度的理论计算公式。杨富斌[15]建立了热力学模型、传热模型、优化模型和热经济性模型，采用遗传算法的方式，对ORC系统的蒸发压力、冷凝温度、过热度进行优化。

以上文献中，大多采用理论分析和数值模拟全局寻优的方式，得到系统的最佳运行参数，在全局寻优的过程中，存在一定的时长，而在实际工程应用中，热源的温度以及环境的变化是一个动态波动的过程，寻优时间的延后对于系统的运行及控制产生很大的影响。

近年来，基于自适应性强、处理非线性问题能力强的优点，人工神经网络方式被广泛用于能量回收系统的设计、运行参数预测和控制。Boukelia[16]等人提出了一种基于BP神经网络优化太阳能回收系统性能方法。王羽鹏[17]等人基于人工神经网络模型研究了ORC系统循环过程的计算。但目前采用人工神经网络对ORC系统进行优化的相关研究较少。本文选择R245fa为有机工质，以净输出功最大为优化目标，采用人工神经网络的方式，研究ORC系统的最佳蒸发温度。通过数值模型获取大量的训练样本进行训练，在给定的热源及环境参数下对系统净输出功对应的最佳蒸发温度进行预测。

1 数值模型

图1和图2分别为有机朗肯循环（ORC）的系统图和-图。ORC系统一般由膨胀机、冷凝器、蒸发器、工质泵四个部件组成。ORC系统的工作过程为：（1）4-1为工质在蒸发器中定压吸热至饱和或过热蒸汽；（2）1-2为工质在膨胀机中膨胀对外做功；（3）2-3为工质在冷凝器中等压放热至饱和液体；（4）3-4为工质被泵加压至蒸发压力。ORC系统循环发电过程中，低温热流体的温度在蒸发器中被冷却至目标温度。

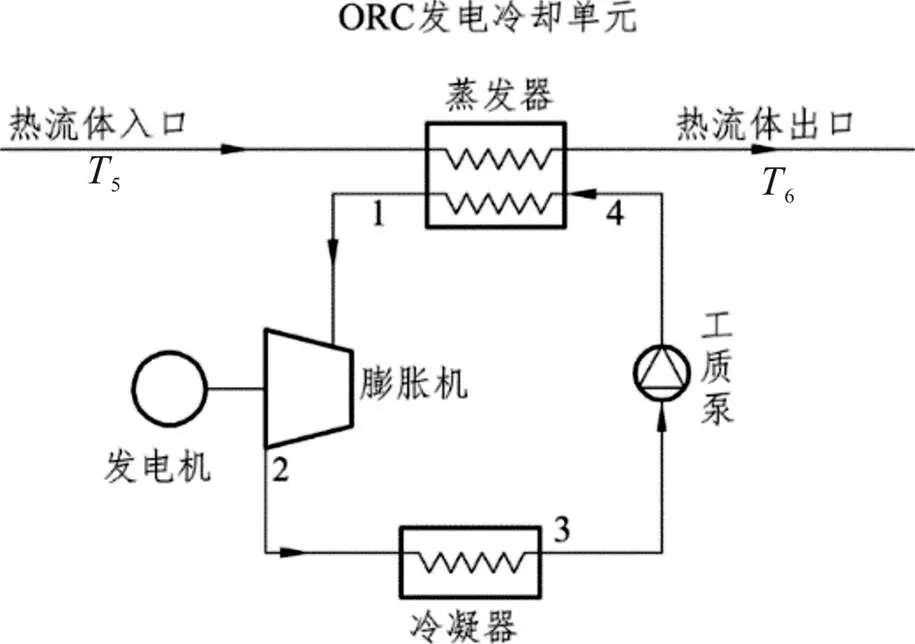
图1 ORC系统示意图

图2 ORC系统运行T-s图

根据文献表明，R245fa具有良好的热力学性能，适用于较广的热源温度范围，且具有良好的环保性能[18-20]，本文选用R245fa作为工质进行基于以下假设，建立ORC的数值模型：

（1）系统处于稳定运行状态；

（2）忽略蒸发器、冷凝器、管道及附件中的压力损失；

（3）蒸发器、冷凝器出口处工质为饱和状态；

（4）膨胀机和工质泵的等熵效率为定值；

（5）发电机发电效率为定值。

1.1 模型建立

（1）蒸发器

有机工质在蒸发器内吸收低温热流体的热量，换热过程计算式为：

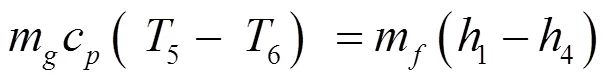
（2）膨胀机

高温高压的有机工质在膨胀机中膨胀做功，计算式如下：

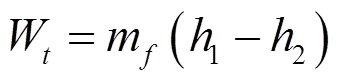
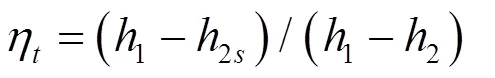
（3）冷凝器

有机工质在冷凝器中的放热量为：

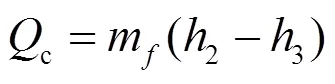
（4）工质泵

工质泵将冷凝器出口的饱和液体加压至蒸发压力，消耗功量如下：

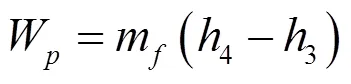
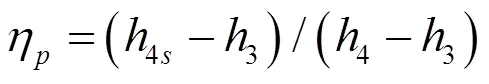
（5）系统净输出功

ORC系统的净输出功如下式所示：

根据文献[13]推导的净输出功公式：

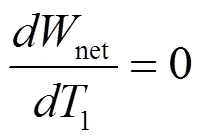
最佳蒸发温度的数学关系式如下式所示：

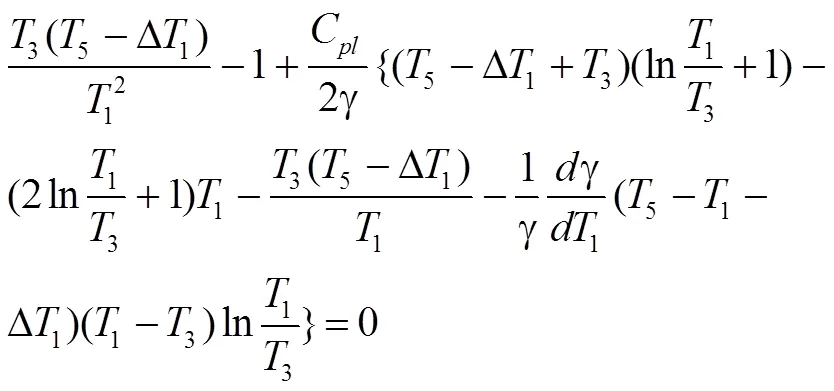
由公式（10）可得，ORC系统的最佳蒸发温度与热源的入口温度，蒸发器的夹点温差，冷凝温度三个参数有关。

1.2 数值模型验证

采用文献[13]的研究结果对本文的ORC系统数值模型进行验证，其中，工质流量为1kg/s，环境温度为293.15K，蒸发器夹点温差为5K，热源入口温度为423.15K。对4种不同工质的最佳蒸发温度进行验证，如表1所示。结果显示，本文数值模型的计算结果与文献结果的相对误差均在0.2%之内，表明本文的数值模型是可靠的。

表1 理论数值模型验证结果

2 神经网络模型

神经网络的全称是人工神经网络，模型结构图如图3所示，主要由模拟人脑的神经元组成，包括输入层、隐层和输出层，工作原理为：基于历史数据的训练，得到神经网络模型从而预测数据。神经网络模型具有良好的自适应性和良好的处理非线性问题的优点[21]。

神经网络模型可用下式表示[22]：

=+（11）

() （12）

式中，是输入参数的权值加和，是激活函数，是输出参数。

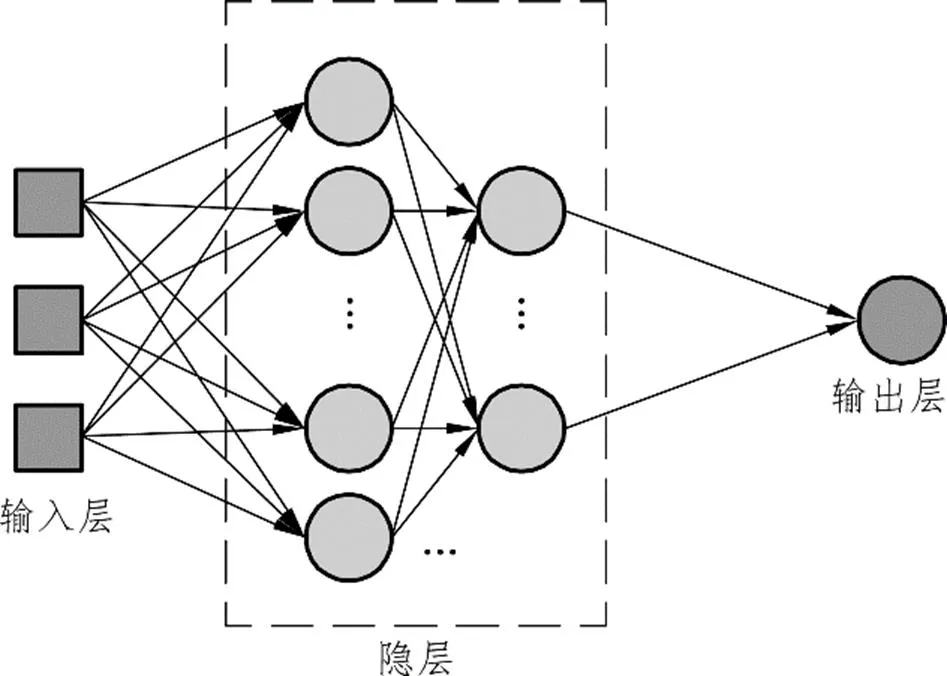
图3 神经网络结构

2.1 BP神经网络

BP神经网络是应用最广泛的神经网络之一[23,24]，是一种误差反向传播的前向神经网络，输入层包含了影响输出层数据的主要因素，通过隐层神经元和传递函数作用于输出层。

2.2 输入层、输出层确定

根据前述的热力学分析，ORC系统的最佳蒸发温度与低温热源的入口温度、蒸发器的夹点温差、以及冷凝温度有关，所以将这三个参数作为输入层的神经元。根据文献[25,26]，蒸发器夹点温差的范围取为3～15K，在获取样本时以2K为步长取值。热源温度的取值范围为(353.15～513.15)K，以3K为步长取值。冷凝温度取值范围为(290.15～320.15)K，以2K为步长取值。如表2所示。

表2 输入层参数取值范围及步长

2.3 神经网络评价标准

为了检验神经网络的预测精度，选择两种较为常用的评价标准。第一种是相对误差，用来检验数据的平均误差，相对误差越小预测精度越高。其计算式如下所示：

第二种是相关系数[24]，用于衡量神经网络预测值和数值计算值之间的相关性，相关系数越大预测精度越高。其计算公式如下所示：

2.4 神经网络模型训练步骤

采用以下步骤编写程序建立神经网络模型，利用数值模型所得的样本数据进行训练，其流程图如下图4所示。

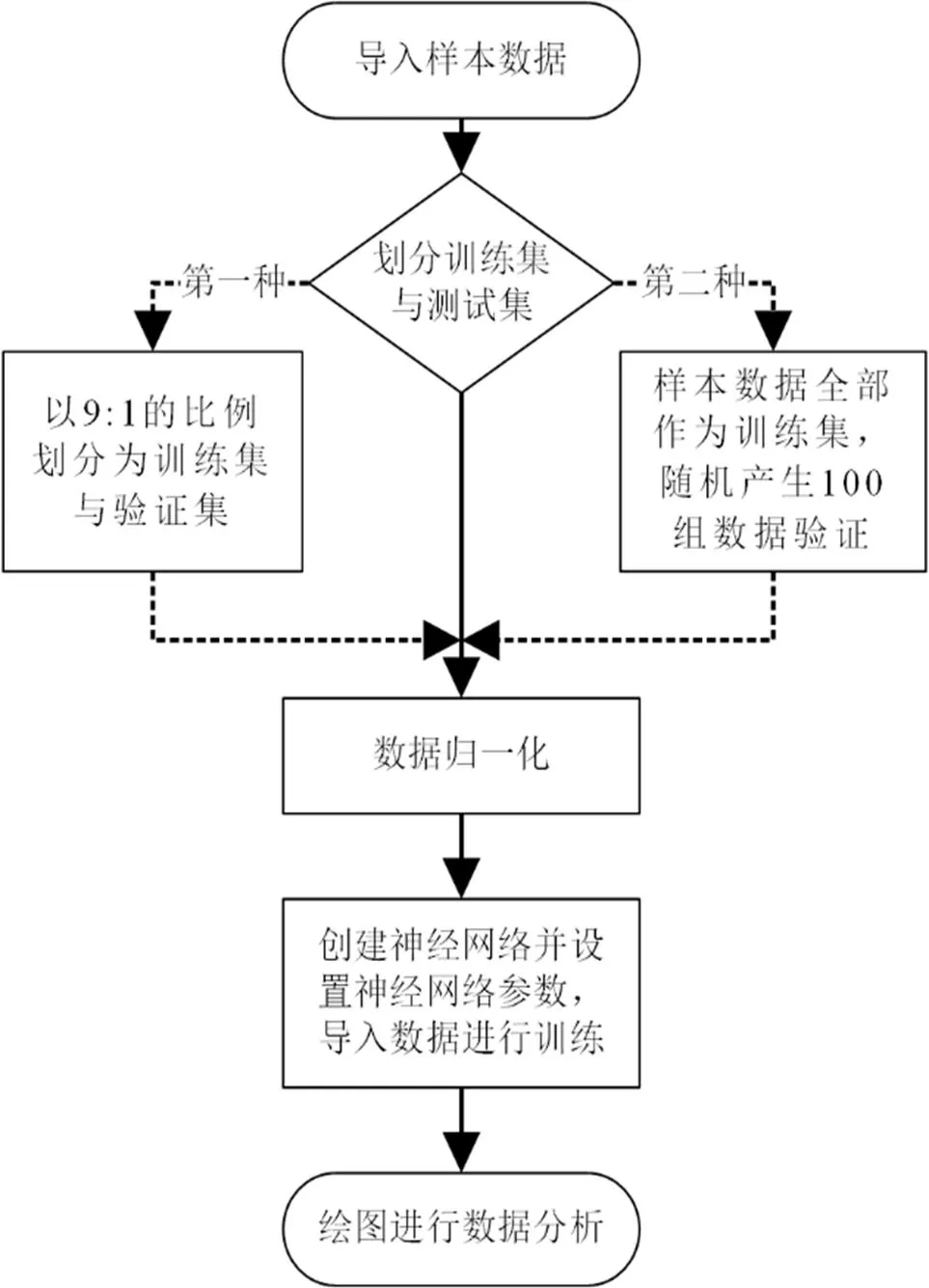
图4 神经网络模型训练程序流程图

2.5 神经网络模型参数确定

本文采用的BP神经网络模型参数如表3所示。

表3 神经网络模型参数

3 结果与讨论

本文基于表2中输入层参数取值范围及步长，采用建立的数值模型计算ORC系统的最佳蒸发温度，将获得的数据集对建立的神经网络模型进行训练，并采用两种方法[22,30]对神经网络模型的预测数据进行验证。

第一种验证方式为：基于表2中输入层参数取值范围及步长，按照9:1的比例随机划分训练集和验证集，将2745组数据作为训练集对神经网络进行训练，其余的305组数据作为验证集对神经网络预测精度进行验证。

第二种验证方式为：将表2中3050组数据全部作为神经网络的训练集进行训练，利用随机数程序在三个输入参数取值范围内随机生成100组数据作为神经网络的验证集。

两种验证方式下，神经网络预测值与数值模拟值的比较分别如图8和图9所示。图中显示，无论验证集是属于表2数据集中的一部分，还是为输入参数取值范围内的随机数，神经网络模型预测值与数值模拟值均较为接近，误差均在2%范围内，表明神经网络可以较好的预测ORC系统的最佳蒸发温度，这说明了神经网络模型在处理ORC系统复杂非线性问题的计算上具有良好的适应性，在ORC系统运行控制的应用上有较大的潜力。

图8 第一种验证方式预测值结果

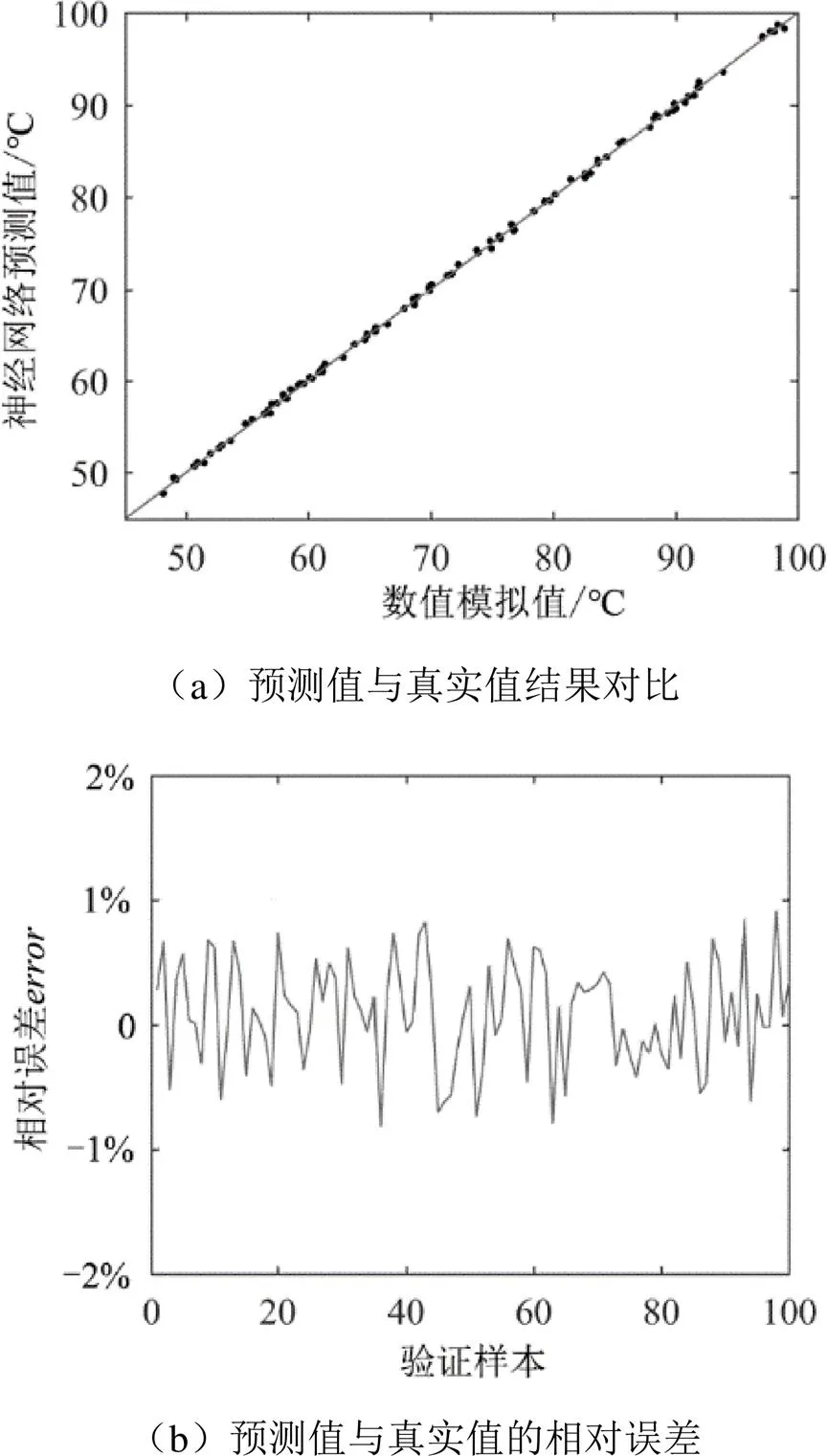
图9 第二种验证方式预测值结果

4 结论

本文以ORC系统净输出功最大为优化目标，通过数值模拟获取大量的训练样本，采用人工神经网络的方式对最佳蒸发温度进行预测，得到如下结论：

（1）神经网络模型中，学习速率、隐层、训练函数的神经元数目对神经网络模型的预测精度有较大影响，经过反复训练得出ORC系统的优化神经网络模型参数，具体为：学习速率为0.4、隐层神经元数目为5、训练函数为基于L-M算法的“trainlm”函数。

（2）采用两种不同的验证方式对训练所得的神经网络模型进行验证，结果显示，神经网络模型预测值与数值模拟值较为接近，误差均在2%范围内，表明神经网络模型可以较好的预测ORC系统的最佳蒸发温度。

[1] 李赛赛,李玉兰.工业冷却循环水节能优化改造[J].节能,2018,37(3):57-58.

[2] Li X, Duniam S, Gurgenci H, et al. Full scale experimental study of a small natural draft dry cooling tower for concentrating solar thermal power plant[J]. Building EnergyEfficiency, 2017,(5):121.

[3] Li W, Chai J, Zheng J. Investigation of Natural Draft Cooling Tower in China[J]. Heat Transfer Engineering, 2017,38(11-12):7.

[4] 中华人民共和国国家发展和改革委员会,科技部,水利部,等.中国节水技术政策大纲[EB/OL].2005.

[5] Cortinovis G F, Pavia J L, Song T W, et al. A systemic approach for optimal cooling tower operation[J]. Energy Conversion & Management, 2009,50(9):2200-2209.

[6] Hung TC, Shai TY, Wang SK. A review of organic rankine cycles (ORCs), for the recovery of low-grade waste heat[J]. Energy,1996,22:661-667.

[7] Wei D, Lu U, Lu Z, et al. Dynamic modeling and simulation of an organic rankine cycle (ORC) system for waste heat recovery[J]. Appl ThermEng, 2008,28:1216- 1224.

[8] Bianchi M, Pascale AD. Parametric investigation of available and innovative solutions for the exploitation of low and medium temperature heat sources[J]. Appl Energy, 2011,88:1500-1509.

[9] Ammare Y, Joyce S. Low grade thermal energy sources and uses from the process industry in the UK[J]. Appl Energy, 2012,89:3-20.

[10] 王梦颖,冯霄,王彧斐.不同余热情况下有机朗肯循环和卡琳娜循环能量性能对比[J].化工学报,2016,67(12): 5089-5097.

[11] 张军辉,刘娟芳,陈清华.有机朗肯循环系统最佳蒸发温度和(火用)分析[J].化工学报,2013,64(3):820-826.

[12] 于浩水.低温余热回收有机朗肯循环系统优化研究[D].北京:中国石油大学,2016.

[13] 贺超.低品位热源驱动的有机朗肯循环性能研究[D].重庆:重庆大学,2013.

[14] 严家禄.低温热能发电方案中选择工质和确定参数的热力学原则和计算式[J].工程热物理学报,1982,3(1):1-7.

[15] 杨富斌.基于热经济性分析人工网络建模的车用有机朗肯循环性能优化[D].北京:北京工业大学,2018.

[16] Boukelia TE, Arslan O, Mecibah MS. ANN-based optimization of a parabolic trough solar thermal power plant[J]. Appl ThermEng,2012,92:492-502.

[17] 王羽鹏,梁俊伟,罗向龙,等.基于神经网络的有机朗肯循环过程及循环性能计算方法[J].化工学报,2019,70(9): 3256-3266.

[18] 韩中合,杜燕,王智.有机朗肯循环低温余热回收系统的工质选择[J].化工学报,2014,33(9):2279-2285.

[19] 刘杰,陈江平,祁照岗.低温有机朗肯循环的热力学分析[J].化工学报,2010,61(S2):9-14.

[20] [20] Bao J, Zhao L. A review of working fluid and expander selections for organic Rankine cycle[J]. Renewable and Sustainable Energy Reviews, 2013,24:325-342.

[21] 代正梅,田建艳.神经网络预测控制综述[J].科技情报开发与经济,2007,17(15):155-157.

[22] Phil Kim. MATLAB Deep Learning: With Machine Learning, Neural Networks and Artificial Intelligence[M]. Korea: Phil Kim, 2017.

[23] Li G, Shi J. On comparing three artificial neural networks for wind speed forecasting[J]. Appl Energy, 2010,87: 2313-2320.

[24] Zhao JX, Xu M, Li M, et al. Design and optimization of an Atkinson cycle engine with the Artificial Neural Network Method[J]. Appl Energy,2012,107:1210-1218.

[25] 魏东红,陆震,鲁雪生,等.废热源驱动的有机朗肯循环系统变工况性能分析[J].上海交通大学学报,2006, 40(8): 1398-1402．

[26] 吴治坚,龚宇烈,马伟斌,等.双工质循环发电系统换热器温度参数选择的研究[J].太阳能学报,2012,33(1): 63-66．

[27] Robert Hechet-Nielsen. Theory of the back propagation neural network[J]. Neural Networks,1988,1(1):445.

[28] 王伟.人神经网络原理：入门与应用[M].北京:北京航空航天大学出版社,1995.

[29] 萨马拉辛荷.神经网络在应用科学和工程中的应用：从基本原理到复染的模式识别[M].北京:机械工业出版社,2010.

[30] Yang FB, Cho Heejin, Zhang HG, et al. Artificial neural network (ANN) based prediction and optimization of an organic Rankin cycle(ORC) for diesel engine waste heat recovery[J]. Energy Conversion & Management, 2018,164:15-26.

Prediction of Optimal Temperature for Organic Rankine Cycle based on Artificial Neural Network

Chen Wei Yuan Zhongyuan

( School of Mechanical Engineering, Southwest Jiaotong University, Chengdu, 610031 )

Optimal temperature of Organic Rankine Cycle (ORC) has been an inevitable parameter in generating maximum net power.Theoretical thermal mathematicalmodel is constructed to obtain optimal temperatures used as training samplesbyaltering heat source temperatures, condensing temperatures and pinch point temperatures. In this paper, artificial neural network (ANN)is installed to predict the optimal temperature to generate maximum power. The result shows that different parameters show great effects on prediction accuracy. Eventually, training rate, nodes number of hidden layer and training function are determined as 0.4, 5, “trainlm”, respectively. After being trained repeatedly, the flowing two different methods are adapted to test accuracy of ANN model: (1) Samples are divided by 9 (training samples):1(testing samples). (2)Generate 100 samples within the ranges of inputs randomly as testing samples.Compared the optimal temperatures obtained bytheoretical thermal mathematical model, the maximum relative errors tested with two different approaches are both less than 2%, which indicates that the proposed ANN model shows a strong ability to parametric optimization and it can be used in practical background.

ORC system; waste heat recovery; optimal evaporationtemperature; neural network

TM617

A

1671-6612（2020）02-262-06

四川省科技计划项目：基于分级冷却的工业余热高效能量回收系统（2019YFG0327）

陈 薇（1996-），女，硕士研究生，E-mail：1481965377@qq.com

袁中原（1983.8-），男，博士，E-mail：zhongyuan.yuan@home.swjtu.edu.cn

2020-03-15