一种小波特征与深度神经网络结合的信号制式识别算法*
2020-06-02唐作栋龚晓峰雒瑞森
唐作栋,龚晓峰,雒瑞森
(四川大学电气工程学院,四川 成都 610065)
1 引言
现代无线通信环境日益复杂,如何在低信噪比的情况下准确识别信号调制方式成为无线通讯领域的一个难题。近年来,在对通信信号调制制式识别的研究中,普遍采用的方法包括基于时频分析的方法、基于特征参数提取的方法、基于高阶累积量的方法、基于统计模式识别理论的方法和基于决策树理论的方法等,取得了一定的效果。其中每种方法单独使用时,受环境噪声的影响较大,分类效果不明显,因此多方法结合进行信号制式识别是研究的热点方向。
文献[1]提出了一种基于高阶累积量和单层神经网络结合信号制式识别算法,通过计算出每种信号的3个特征参数,用单层神经网络作为分类器,实现了对常见数字信号的分类。文献[2]提出了基于小波神经网络统计模式识别的方法,该方法识别系统较为复杂、计算层数多,在较高信噪比条件下才能达到理想识别效果。文献[3]结合了通信信号的时频特性和卷积神经网络,减少了训练时间,在一定程度上提高了信号的识别率。文献[4]提出一种基于K均值聚类和分级支持向量机相结合的识别算法,提取了5个特征参数,主要对{2PSK、4PSK、8PSK、16QAM、32QAM、64QAM}信号进行识别,在信噪比为5 dB时,识别率达到90%。文献[5]提出一种将信号的星座图作为输入的卷积神经网络的识别算法,通过白化增强的星座图在卷积神经网络中进行特征的自动提取,对{2PSK、4PSK、OQPSK、4ASK、8PSK、16QAM、32QAM、64QAM}信号进行识别,在信噪比为4 dB时,平均识别率达到92%。文献[6]提出一种基于分数低阶循环谱相关系数的数字调制识别新方法,研究提取出5个特征系数作为特征参数,用决策树分类器对非高斯环境下的数字调制信号进行识别。文献[7]采用一种归一化四阶累积量的统计特征的识别方法,对{MPSK、MQAM}信号进行了分类。文献[8]提出一种结合高阶累积量和分层多项式结合的分类方法,减少了需要的信号码元数,在20 dB情况下识别率达到100%。文献[9]提出了一种新的基于分形理论及多分类最小二乘双支持向量机的通信信号识别方法,在信号信噪比大于-5 dB时,平均识别率达到91%以上。文献[10]基于深度学习的多进制相移键控信号调制识别方法提出一种估计信道和噪声参数的方法,在一定程度上提高了信号的识别性能。文献[11]针对MPSK信号,提出了一种根据信号的二次幂和四次幂的傅里叶变换的图形特征,在实际信道中对信号进行识别的方法。
针对在低信噪比情况下识别不准确的问题,本文提出一种结合小波特征与改进的深度神经网络WL-DNN(WaveLet Deep Neural Network)的信号制式识别算法,采用基于小波变换的特征提取方法,对信号进行小波分解重构,提取出滤去噪声后的“干净”信号,计算出3种新的小波特征参数。通过训练具有多层隐含层的弹性BP神经网络作为信号制式识别的分类器,并在Matlab 2016仿真平台上进行验证,选取分类结果最优的隐层数。选择实验模拟仿真出的实际接收到的信噪比较小的信号作为辐射信号源,利用本文提出的算法,实现了2ASK、4ASK、2PSK、4PSK、2FSK、4FSK、OFDM、AM、FM、16QAM等10种信号的分类。该算法充分利用小波变换良好的抗噪声性能,减少了特征参数个数,提高了识别率,降低了算法的复杂度。理论分析和仿真结果表明,该算法能有效对这10种调制信号进行识别,且识别效果良好。
2 小波变换理论
2.1 信号模型
数字通信中常见的调制方式有幅移键控(ASK)、频移键控(FSK)、相移键控(PSK)和正交频分复用(OFDM)等。在数字通信系统中,对这些调制信号进行分析,设接收到的信号的复数形式可表示为:
(1)

(2)
(3)
ωi∈{(2m-1-M)Δω,m=1,2,…,M}
(4)
Ei=ai+bi,φi=arctan(bi/ai) mod 2π
(5)
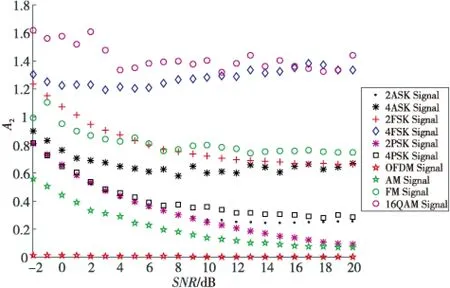
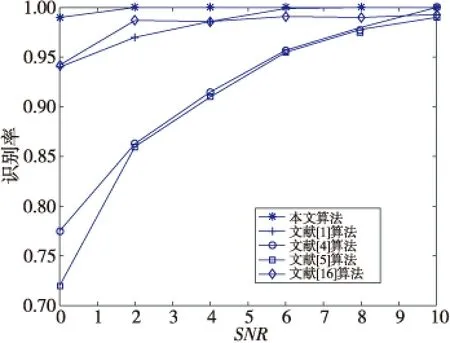
ts (6) 其中,E表示发送码元波形的能量;M表示信号调制阶数;Ts表示符号周期;p(t)表示基带信号波形;Δω表示频率偏移量;ai,bi表示QAM信号的同相、正交分量;C表示子信道个数;di表示分配给每个子信道的数据符号;ts表示OFDM信号从t=ts时刻开始。 小波变换具有可以解析信号的细微变化和在时频2域都能表征局部时变状态的优点。常见通信信号的有效信号多集中在低频部分,而干扰信号多集中在高频部分,因此小波分析更利于低信噪比信号的特征提取。通信信号的调制过程中,在码元交接处往往存在着信号瞬时突变的情况,包括幅度参量的突变、频率参量的突变和相位参量的突变。由于小波变换具有多分辨率的特点,通过尺度伸缩和平移可以很好地体现出信号的局部瞬态信息,将信号突变部分检测出来[12,13]。 信号的连续小波变换(CWT)定义为: (7) 其中Ψ*为小波基函数,a为尺度因子,τ为位移因子。本文选用Haar小波作为小波基函数,其特点是函数简单,对相位的变化具有较好的识别性[8],其表达式为: (8) 当数字信号无瞬态变化时,小波变换的输出是一个恒定的值,这与尺度因子有关;当信号发生突变时,小波变换的输出就会发生明显的变化[14,15]。所以,Haar小波作为小波变换的基函数是合适的。 利用小波变换的分解重构算法,分解出信号的低频信息、近似分量和高频信息、细节分量,计算出小波分解的默认阈值,再重构出去除噪声后的“干净”信号,流程图如图1所示。 Figure 1 Flow chart of wavelet denoising图1 小波去噪流程图 将信号进行小波分解、去噪、重构后,高斯白噪声得到很大程度的消除,波形形状趋于稳定、平滑。再选取能反映信号瞬时特征的参数,则特征更具有区分度和可靠性。 特征参数A1是归一化瞬时幅度方差,先将调制信号进行中值滤波,再计算其特征值。该特征反映信号的波动程度,对瞬时幅度变化较大的2ASK、4ASK等有较好的识别能力,其表达式为: (9) 特征参数A2为小波变换后的归一化瞬时幅度标准偏差,该特征采用经过小波变换和幅度中值滤波后的瞬时幅值进行计算,既平滑了噪声干扰也更能反映出信号局部波动的特征。该特征对一个符号区间内归一化中心瞬时幅度为零和不为零的调制方式(OFDM、MPSK、MFSK)具有较好的识别能力,其表达式为: (10) 其中,c(i)表示小波变换后的归一化瞬时幅值,N表示采样数。 特征参数A3为经过3层小波去噪后的归一化瞬时幅值绝对值标准偏差,表征信号的绝对幅度信息,用来表示数据的离散程度,对具备和不具备归一化的绝对幅度信息的调制方式(AM、FM)具有较好的识别能力,其表达式为: (11) 其中,X(i)是3层小波去噪后信号归一化瞬时幅值,N是采样数。 BP神经网络是一种多层前馈神经网络,分为输入层、隐含层和输出层,由于其结构简单、可塑性强,在实际工程中应用更为广泛。 本文选用了多隐含层的深度BP神经网络作为调制识别算法的分类器。在进行算法分类测试时,分为了训练过程和测试识别过程。训练过程为:首先,将提取好的特征参数作为训练样本输入神经网络,经过输入层、隐含层和输出层的计算后,得出输出结果,并与样本标签进行比对,计算均方误差。再将误差进行弹性反向传播,即在反向传播的过程中添加上次迭代参数的加权值,通过梯度下降策略,以减小均方误差为目的,修正输入层至隐含层、隐含层至输出层的连接权值和节点阈值,并不断循环这个过程,直到均方误差收敛到预期目标值,或者达到最大训练次数。测试识别过程为:首先计算待识别的调制信号的特征参数,并将其作为测试样本输入已经训练好的神经网络,然后得到神经网络的输出结果。 输入层含有3个神经元,对应调制信号提取出的3个特征参数。隐含层为3层时,每层分别有12,24,12个神经元;隐含层为4层时,每层分别有12,24,24,12个神经元;隐含层为5层时,每层分别有12,24,24,24,12个神经元。输出层的神经元个数为4个。4个输出最多可以产生16个标签,选取10个标签分别对应待识别的10种调制信号。隐含层的神经元个数选取得过大或过小都会导致神经网络训练时出现一定的问题,故根据经验值选取恰当的隐含层神经元个数。识别系统模型如图2所示。 Figure 2 Recognition system model图2 识别系统模型 为了验证改进后的分类算法对各类数字调制信号的分类性能,在Matlab 2016平台上进行仿真实验。首先模拟产生接收机接收到的含噪声干扰调制信号,仿真采用随机二进制信号源,信号的采样频率为200 kHz,信号的载波频率为20 kHz,码元数为100组,每个码元中含有1 000个数据点。然后研究不同信噪比下,计算出的特征参数的变化趋势。再通过将不同信噪比下的特征数据,导入训练好的神经网络分类器,对比分析算法的识别结果。 含有噪声的调制信号在小波分解重构后会取得较好消噪效果。信号中加入的噪声种类是高斯白噪声。调制信号在加入高斯白噪声后,波形的幅度起伏会发生较大改变,波形趋于不稳定和非周期、非平滑状态。噪声较大时,会掩盖原始信号中的特征信息。通过小波分解重构后的信号,波形白化,尖峰和毛刺减少且更平滑。信号经过小波分解重构,滤去噪声的对比效果如图3所示。 特征参数A1随信噪比SNR变化如图4所示。可以看出10种信号的特征参数A1从信噪比大于-2 dB开始,便呈现出稳定的变化趋势,并随着信噪比的变大,各信号间的区别更加明显。这表明了特征参数A1的正确性。 Figure 3 Comparison of wavelet denoising for modulated signals图3 调制信号的小波去噪比较 Figure 4 Characteristic parameter A1 variation with SNR图4 特征参数A1随信噪比变化 特征参数A2随信噪比的变化如图5所示。可以看出10种信号的特征参数A2从信噪比大于-2 dB开始,便呈现出稳定下降的变化趋势,且信噪比大于0 dB时,各信号间的特征出现了稳定的分层,易于分类器识别。这表明了特征参数A2的正确性。 Figure 5 Characteristic parameter A2variation with SNR图5 特征参数A2随信噪比变化 特征参数A3随信噪比的变化如图6所示。可以看出10种信号的特征参数A3从信噪比大于-2 dB开始,便呈现出分层的态势,且信噪比大于6 dB时,部分信号间的特征值出现了上升的趋势。这表明了特征参数A3的正确性。 Figure 6 Characteristic parameter A3variation with SNR 图6 特征参数A3随信噪比变化 进行信号综合测试时,选用10种信号,SNR取-2 dB~20 dB,每个SNR下各取100组信号特征作为原始数据,随机提取一半作为训练样本,一半作为测试样本。将训练样本输入BP神经网络进行分类器训练,当均方误差收敛到理想值后,输入测试样本进行测试。测试分类结果如图7所示。 Figure 7 Classification results in three-dimensional feature space图7 三维特征空间中的分类结果 根据本文算法的分类结果,10种不同的符号代表10种不同的信号,不同调制方式的信号在三维特征空间中被完全识别分类,总共出现了6个误分样本。结果表明本文算法进行信号综合识别时,10种信号在特征空间中能被同时识别,误识别率低。 在进行信号识别率统计实验时,先搭建好多隐含层的神经网络分类器,将10种信号在信噪比为-2 dB~20 dB下的特征各50组输入各个神经网络训练10次,得到训练好的10*3个神经网络。再将10种信号在每个信噪比下的100组数据作为样本,分别输入10*3个训练好的神经网络进行测试,即每种信号在各信噪比下测试1000*3次,计算测试结果。 比较分析深度神经网络的不同隐含层数,在不同信噪比条件下对平均识别率的影响。由实验统计结果可得,改进的BP神经网络的隐含层数为3层时,对10种信号的识别率进行了测试统计,最低的信号识别率为95.5%;用同样的统计测试方法,网络的隐含层数为4层时,最低的信号识别率为79.2%;网络的隐含层数为5层时,最低的信号识别率为91.3%。故分析可得本文算法最优的神经网络隐含层数为3。 不同隐含层数识别结果对比如图8所示。单隐含层的神经网络出现欠拟合,导致识别率降低。隐含层数大于5层,平均识别率会呈现下降趋势,说明隐含层深度越深,会导致神经网络过拟合,识别率降低。隐含层数为3~5层时,平均识别率最优。 Figure 8 Classification results comparison under different numbers of hidden layer图8 不同隐含层数识别结果对比 本文采用的信号噪声为加性高斯白噪声,在较低信噪比的条件下取得了良好的识别效果,与其他主流算法识别率的比较如图9所示。 Figure 9 Different algorithms’ classification results comparison图9 不同算法识别结果对比 通过对比可知,文献[1]采用的高阶累积量与小波变换结合的算法在信噪比高于2 dB时识别率达到95%以上;文献[4]采用的K均值聚类与支持向量机结合的算法,信噪比在6 dB以上时,识别率达到95%以上;文献[5]采用的星座图与卷积神经网络结合的算法,信噪比在6 dB以上时,识别率达到95%以上;文献[16]采用稀疏滤波神经网络的算法,将信号进行稀疏滤波处理,再用卷积神经网络进行识别,信噪比在2 dB以上时,识别率达到95%以上;本文算法的平均识别率在信噪比为0 dB时达到98.5%,实现了在低信噪比条件下的多个调制信号的准确识别。 对本文算法、文献[1]算法、文献[4]算法、文献[5]算法和文献[16]算法进行算法复杂度分析。 (1)本文算法(WL-DNN)包括信号分解重构、信号特征提取、弹性深度神经网络训练3个环节。设每种信号矩阵大小为1*n,n为1次循环的计算次数。3层小波分解重构的时间复杂度为O(3n),信号特征提取的时间复杂度为O(n),深度神经网络的层数为K,则训练的时间复杂度为O(K*n)。总时间复杂度为O(3n)+O(n)+O(K*n)。 (2)结合文献[1]算法:高阶累积量的特征计算时间复杂度为O(n),小波变换的特征计算的时间复杂度为O(n),单层神经网络的时间复杂度为O(n)。总时间复杂度为O(n)+O(n)+O(n)。 (3)文献[4]算法包括基于聚类算法的特征提取、SVM分类器训练。聚类中心为6阶,特征提取的时间复杂度为O(6*n2),SVM个数为5,分类器的时间复杂度为O(5*n)。总时间复杂度为O(6*n2)+O(5*n)。 (4)文献[5]算法:3通道星座图计算的时间复杂度为O(3*n2),AlexNet卷积神经网络的时间复杂度为O(2*n2+3n)。总时间复杂度为O(3*n2)+O(2*n2+3n)。 (5)文献[16]算法:二维降噪循环谱计算的时间复杂度为O(n2+n),稀疏滤波CNN计算的时间复杂度为O(3*n2)。总时间复杂度为O(n2+n)+O(3*n2)。 在保证训练样本和测试样本一致,计算机条件一致的情况下进行算法耗时计算,本文算法训练网络和测试样本总耗时约为63 s,文献[1]算法训练网络和测试样本总耗时约为45 s,文献[4]算法训练网络和测试样本总耗时约为253 s,文献[5]算法训练网络和测试样本总耗时约为301 s,文献[16]算法训练网络和测试样本总耗时约为186 s。通过比较可以得出,虽然本文算法不是耗时最短的,但是仍具有一定的优势。 本文研究了不同调制信号的特点,提出一种基于小波变换瞬时特征提取与改进的深度神经网络结合(WL-DNN)的识别算法。将信号进行3层小波去噪处理后,选用了3个小波特征参数,再分别用含有3~5层隐含层的深度神经网络作为分类器,进行信号调制制式识别。实验结果表明,本文算法在低信噪比的条件下识别准确率高,算法复杂度低,易于工程实现。在信噪比为0 dB时,单个信号最低识别率超过95%,平均识别率超过98%。2.2 小波分解重构理论
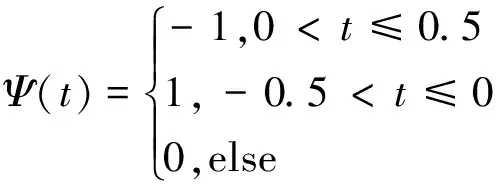

3 算法设计
3.1 基于小波变换的特征参数提取

3.2 深度神经网络设计

4 性能与仿真分析
4.1 信号的小波去噪
4.2 调制信号的特征提取分析



4.3 识别结果


4.4 其他算法对比分析
5 结束语
