薄壁钢板自冲铆接受剪性能及承载力 计算方法研究
2020-06-01谢志强张爱林闫维明张艳霞慕婷婷
谢志强,张爱林,闫维明,张艳霞,虞 诚,慕婷婷
(1. 北京建筑大学土木与交通工程学院,北京 100044;2. 北京工业大学工程抗震与结构诊治北京市重点试验室,北京 100124; 3. 北德克萨斯大学工程技术学院,美国,德克萨斯州 76207;4. 中冶建筑研究总院有限公司,北京 100088)
冷弯薄壁型钢结构因其具有轻质高强、绿色环保、保温隔热、部分构件可生产工业化等优势,近年来在国内外的低层、多层及装配式结构领域中得到了较广泛应用[1]。自攻螺钉是该体系中最常用的连接方式,其性能直接决定整体结构的力学性能[2]。国内外大量研究发现:1) 地震作用下,冷弯薄壁钢结构主要表现为螺钉连接的失效,导致其构件的抗震潜力得不到充分发挥;2) 螺钉连接在受力过程中易发生倾斜与滑移,导致其构件的滞回曲线呈现明显的捏拢效应且耗能能力较差;3) 螺钉连接需要进行钢板夹紧、钻孔、拧螺钉等步骤,其工序较为复杂,严重影响冷弯型钢构件的连接效率与自动化程度,导致该结构难以实现工业化生产并大量推广应用[3―4]。因此,引入新型连接方式是改善冷弯薄壁型钢结构抗震性能,提高其构件连接效率及促进工业化生产实施的有效途径。
自冲铆接是汽车及机械工程领域中的一种常见的连接方式,具有强度高、刚度大、连接效率高及抗疲劳性能好等优点[5]。其成型机理(见图1)为铆钉在上冲模的作用下穿透上层板材,刺入下层板材,在下凹模作用下形成变形铆钉与板材相互镶嵌的内锁机构[6]。
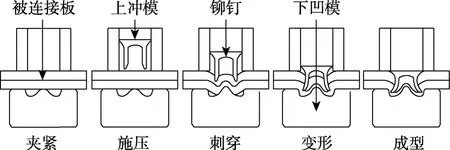
图1 自冲铆接的成型机理 Fig.1 Forming mechanism of SPR joint
国内外汽车与机械工程领域的学者采用数值和试验方法对自冲铆接的成型机理、质量评估准则的研究较为成熟。Amro 等[7]、Ma 等[8]研究了连接板的强度差和厚度、铆钉参数、模具参数对自冲铆接成型机理的影响。结果表明:当上述因素与连接板特性相互匹配时,自冲铆接才会呈现出成型质量较优的内锁机构。Xu[9]和He 等[6]针对家电领域及机械工程领域的需求分别提出定性与半定量的质量评估准则。实际工程中自冲铆接的受剪承载力计算方法大多采用欧洲规范中拉铆钉连接计算方法[10];在汽车领域,Han 等[11]研究表明自冲铆接的受剪承载力取决于铆钉头与上层板的承压能力,而受拉承载力取决于内锁机构的剪切能力;在机械领域,Haque 等[12―13]发现其承载力由内锁长度决定,提出了计算内锁长度的方法;在后续研究中[13],基于横截面参数提出了自冲铆接的受剪承载力计算公式。邢保英等[14]研究了铆钉分布形式对铝合金自冲铆接力学性能的影响;闫维明和谢志强等[15―17]基于传染病传播动力模型提出了自冲铆接的受剪本构模型及承载力计算方法。
综上研究现状可知,汽车与机械领域中对硬度低、延展性大的薄板自冲铆接研究较多,而强度和硬度高、延展性相对较低的薄壁钢板自冲铆接的力学性能及机理不明确;各领域对自冲铆接的性能要求相差甚大,且影响其力学性能的因素较多,钢结构领域尚无相关承载力计算方法。为将效率与自冲化程度高的自冲铆接应用于薄壁钢结构中的构件连接,本文对51 组薄壁钢板自冲铆接试件进行受剪性能试验;研究了钢板厚度、厚度比和铆钉长度对其受剪性能和破坏机理的影响规律,提出了钢板组合厚度与铆钉长度间的经验公式;分析了现有自冲铆接受剪强度计算方法和各国规范关于自攻螺钉连接受剪承载计算方法的适用性;基于试验和分析结果,针对不同破坏模式的自冲铆接,提出了适用于设计的受剪承载力计算方法。上述研究以期可为冷弯薄壁型钢结构中薄壁构件的连接提供一种工业化程度与效率高的新型连接方式。
1 国内外受剪承载力计算方法分析
1.1 欧洲规范拉铆钉连接受剪设计计算方法
目前,自冲铆接的受剪承载力设计方法大多采用欧洲规范拉铆钉连接的受剪承载力计算方法[10]:
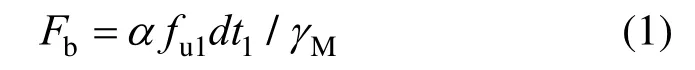
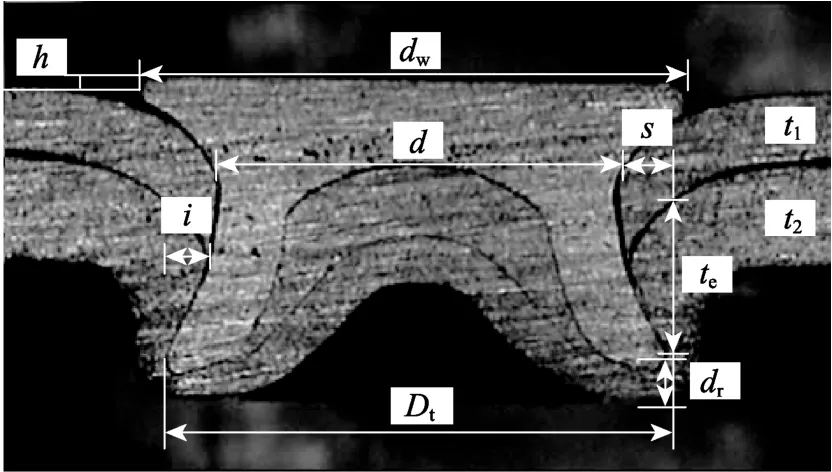
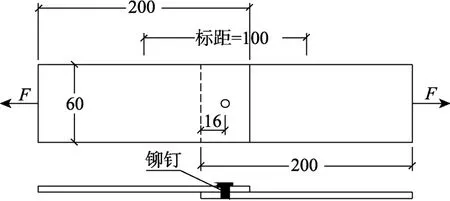
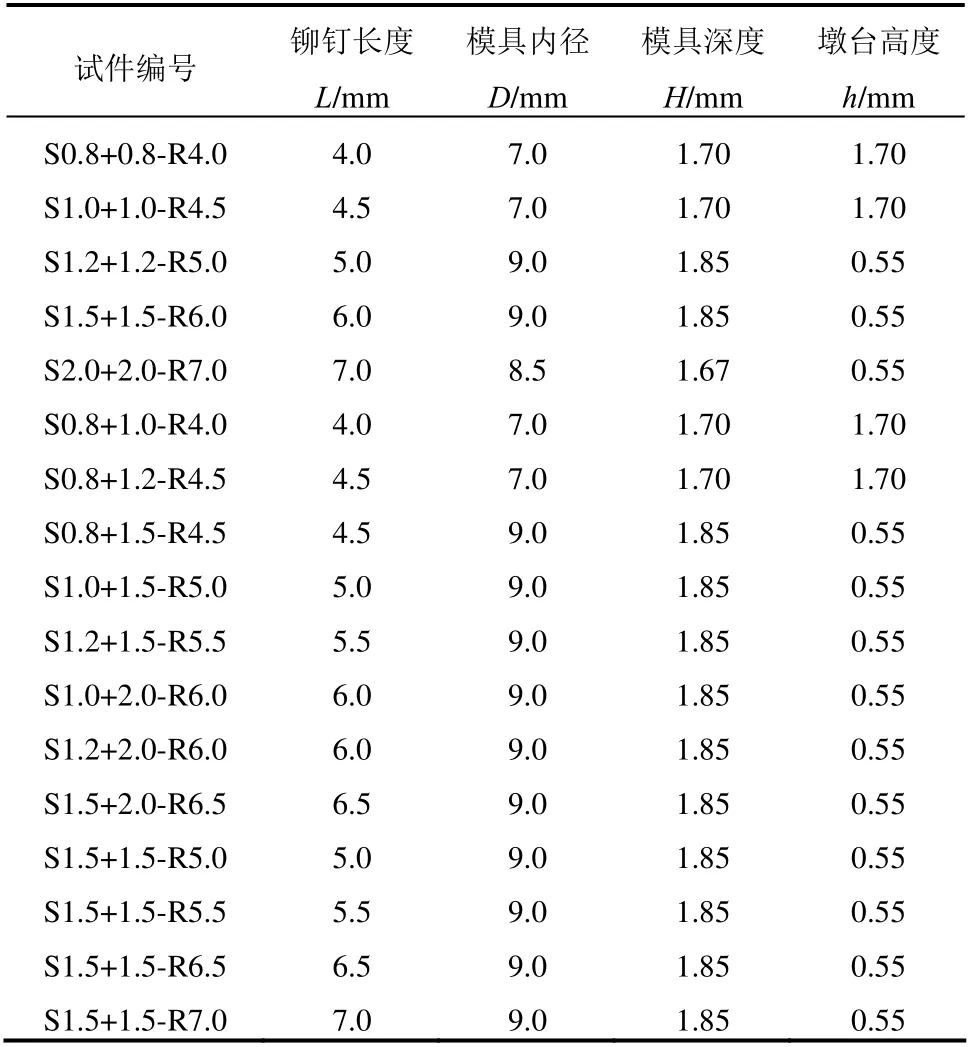
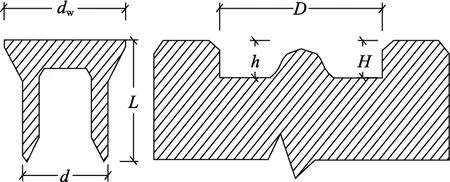
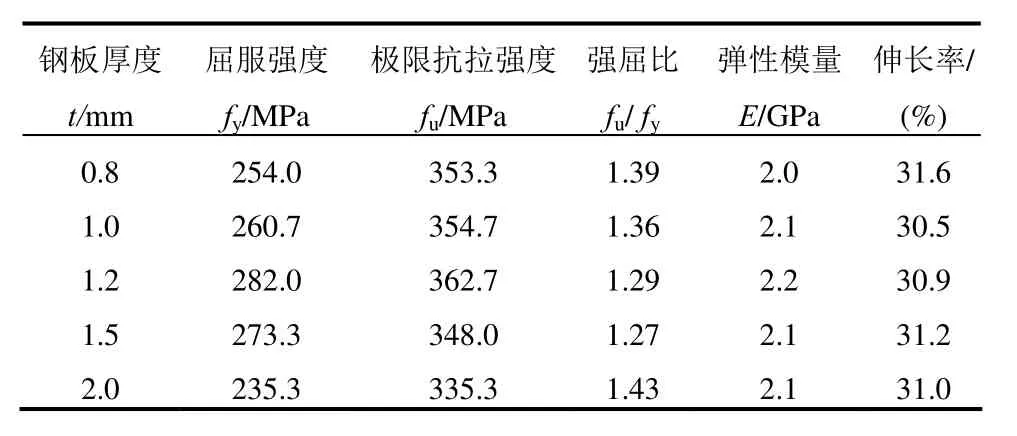
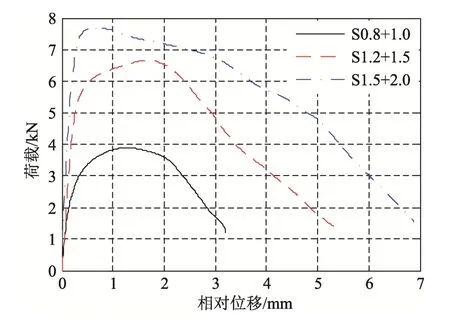
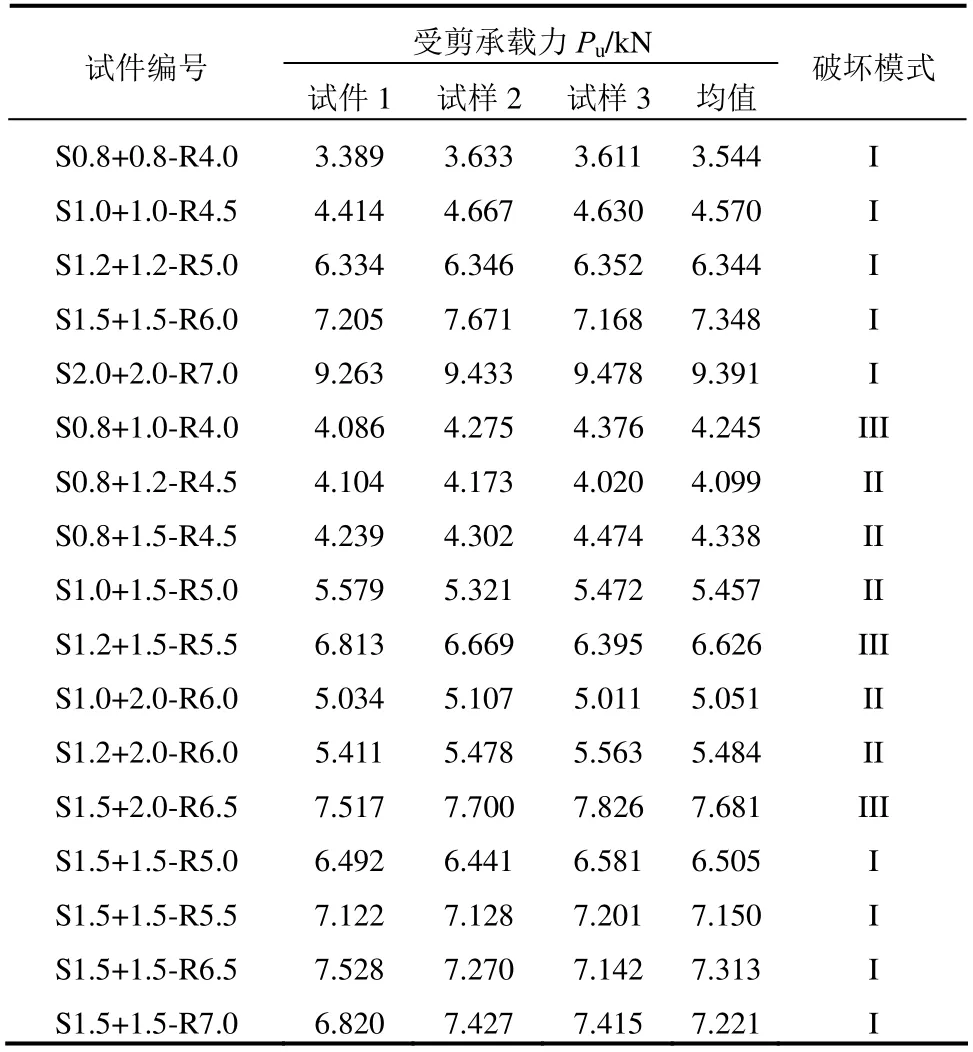
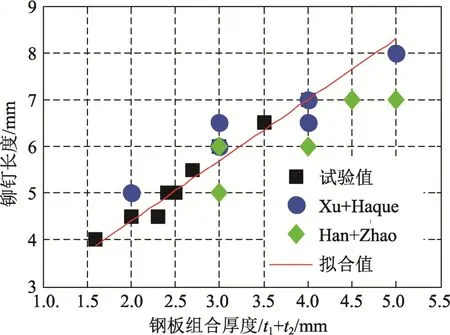
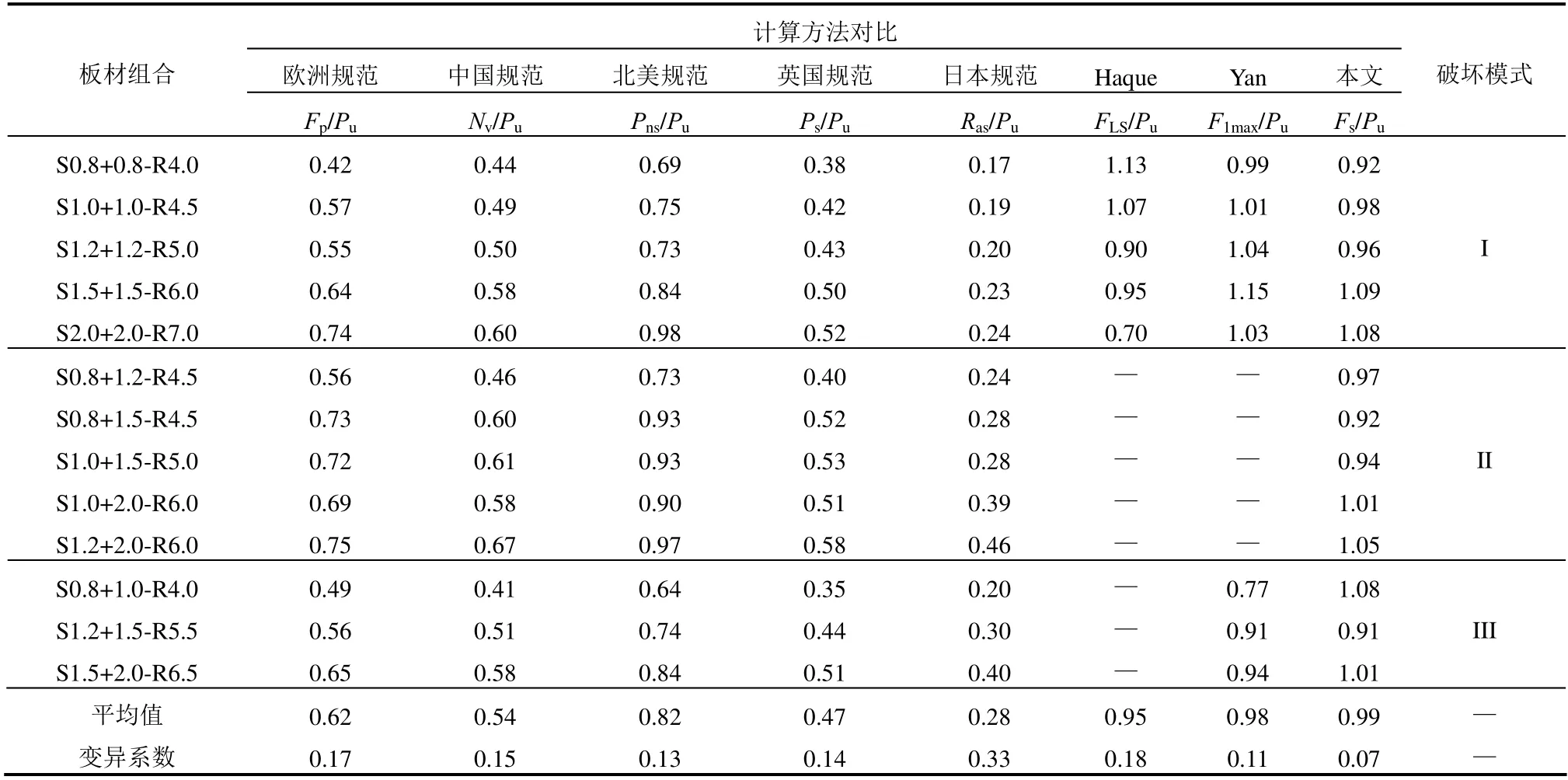
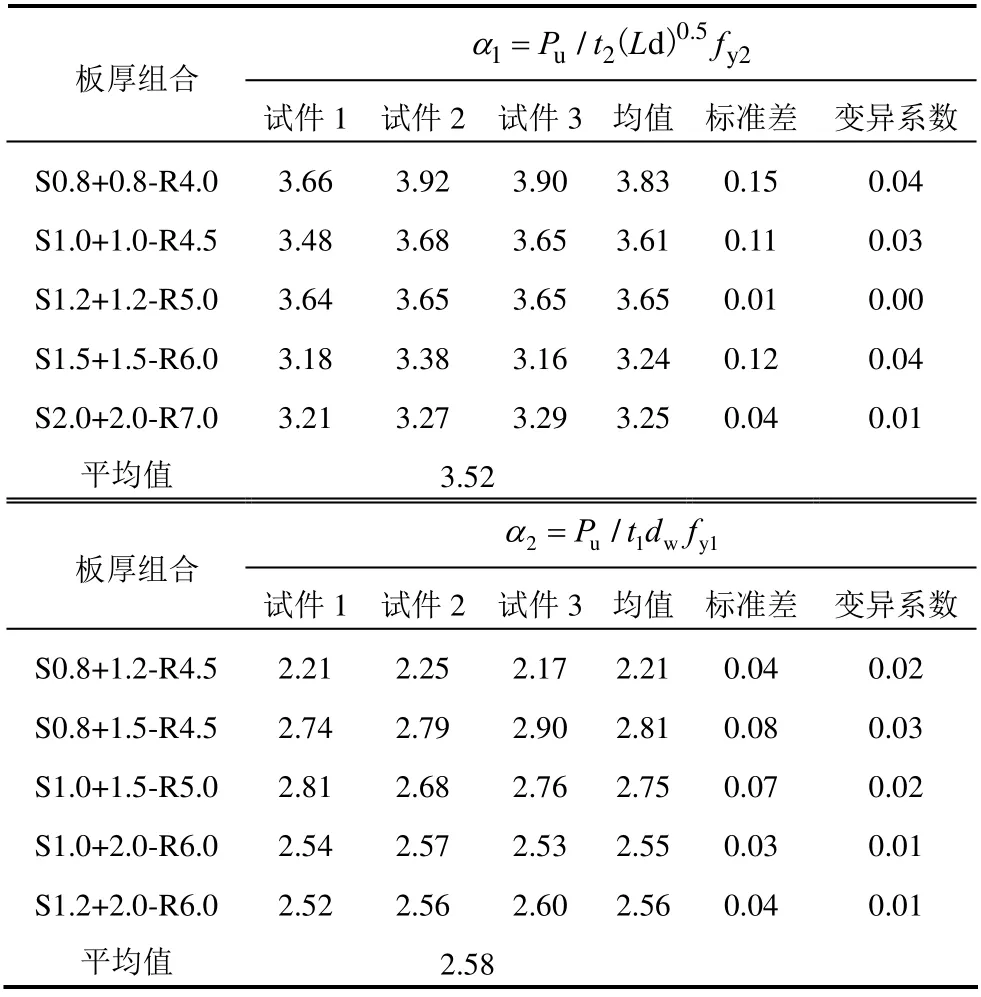
式中:Fb为拉铆钉连接的承压破坏承载力;fu1为母材的极限抗拉强度;d为铆钉直径;t1为较薄板的厚度;t2为较厚板的厚度;γM为影响因素系数,取1.25;α为计算系数,当t2/t1=1 时,α=3.2(t1/d)0.5且α≤2.1;当t2/t1≥2.5 时,α=2.1;当1 机械工程领域中的Haque 等[12]发现自冲铆接的受剪强度主要由内锁机构中的内锁长度决定,并推导出了计算内锁长度的经验公式;在其后续的研究中[13]通过对中心截面参数进行分析,进一步发现自冲铆接的受剪强度与变形铆钉直径(Dt)和底板有效厚度(te)有关,并提出经验公式如下: 式中:FLS为自冲铆接的受剪强度;αLS为计算系数,取1.8;σt为被连接板的屈服强度;H为底模深度;图2 给出了铆接剖面图,其中心截面参数定义如下:钉头高度h、钉头直径dw、钉管直径d、内锁长度i、底板有效厚度te、铆钉张开度S、变形铆钉直径Dt、残余底厚dr、t1和t2分别为顶板和底板厚度。 图2 自冲铆接接头剖面图 Fig.2 Profile drawn of SPR joint 然而,式(4)仅适用于相同板厚组合下铆钉腿拔出下层钢板的破坏模式,对于不等厚钢板组合的其它破坏模式则不适用;且其计算方法是基于中心截面测量的参数,计算精度取决于中心剖面几何参数的测量误差,不便于指导设计。 Yan 等[16]基于传染病传播动力模型提出了适用于冷弯型钢结构的自冲铆接受剪强度设计方法,其计算公式如下: 式中:F1max为自冲铆接的受剪强度;t1、t2分别为上、下层板材的厚度;ξ为考虑铆钉长度影响的修正系数,ξ=0.9;d为铆钉直径;α、β、γ为反映内锁机构力学性能的参数;f为连接板材的抗拉强度。 然而,式(5)仅适用于板厚比小于1.5 的情况,即铆钉腿拔出下层钢板的破坏模式,而对于板厚比大于1.5 时的其它破坏模式不适用。因此,可在此基础上进一步改进,提出一种能考虑不同破坏模式的自冲铆接受剪强度设计方法。 1) 中国规范GB 50018―2002 规定[2]: 自攻螺钉连接在螺钉倾斜、板材撕裂破坏模式下,其受剪承载力设计值可由如下方法确定: 当21/ 1t t= 时: 且 当t2/t1≥ 2.5时: 当 1 ≤t2/t1≤ 2.5时:由式(6)和式(8)插值求得。 2) 北美 AISI S100―2016 与澳洲 AS/NZS 4600―2005 的规定[18―19]类似: 式中:Pns为单颗螺钉的名义受剪强度;d为螺钉直径;t1、t2分别为与钉头接触侧和不与钉头接触侧构件的厚度;Fu1、Fu2分别为与钉头接触侧和不与钉头接触侧构件的抗拉强度。 当t2/t1≤ 1时:Pns取式(9)、式(10)、式(11)的较小值; 当t2/t1≥ 2.5时:Pns取式(10)、式(11)的较小值; 当 1 <t2/t1< 2.5时:Pns由上述两种情况通过插值求得。 3) 英国规范BS 5950-5―1998 规定[20]: 当t2/t1= 1时: 且 式中:Ps为单颗螺钉连接的受剪强度;d为螺钉直径;t1、t2分别为与钉头相邻侧和不与钉头相邻侧构件的厚度;Py为被连接钢板的抗拉强度设计值。 当t2/t1≥ 2.5时: 当 1 ≤t2/t1≤ 2.5时:Ps由式(12)和式(14)插值求得。 4) 日本轻型薄板钢结构设计手册[21]对自攻螺钉连接件的受剪承载力设计计算方法规定如下: 式中:Ras1为螺钉倾斜的受剪承载力;Ras2为与钉头接触侧板材的承压力;Ras3为不与钉头接触侧板材的承压力;Ras4为螺钉剪断力;Ras为螺钉连接的受剪承载力;η为调整系数;d为螺钉直径;te1、te2分别为与钉头接触侧和不与钉头接触侧钢板的计算厚度;F1、F2分别为与钉头接触侧和不与钉头接触侧钢板的抗拉强度设计值;fs为螺钉受剪强度设计值;Ad为螺钉截面面积。 综上各国规范可知:螺钉连接受剪承载力设计方法主要针对螺钉倾斜、板材撕裂两种破坏模式;此外,日本规范还考虑了螺钉剪断破坏下的承载力计算方法。由于自冲铆接和螺钉连接的成形机理与力学性能相差甚大,故自攻螺钉连接受剪计算方法直接应用于自冲铆接的可行性不明确,但其破坏模式分类与公式形式具有较大的借鉴意义。 本文用常见厚度的薄壁钢板设计制作了51 个自冲铆接抗剪连接试件,其考虑了钢板厚度、厚度比、铆钉长度因素。自冲铆接试件采用0.8 mm、1.0 mm、1.2 mm、1.5 mm、2.0 mm 厚的镀锌钢板组合,钢板型号均为DX51D+Z25。参考AISI TS-4―2002[22]对自攻螺钉连接的测试方法,自冲铆接抗剪试件的钢板长度取200 mm,宽度取60 mm,铆钉端距取三倍铆钉直径16 mm。试验试件示意图见 图3。 图3 自冲铆接抗剪试件示意图 Fig.3 Schematic diagram of the shear specimen of SPR 自冲铆接在锁铆设备上完成,采用的铆钉及模具尺寸定义如图4 所示。基于前期大量自冲铆接接头的质量评估测试,确定了不同钢板组合厚度下试件的铆钉参数及模具型号。试件编号及所采用的铆钉和模具参数如表1 所示。其中,试件编号的规定如下:例如S0.8+1.5-R4.5,“S0.8+1.5”表示上、下层钢板的厚度分别为0.8 mm、1.5 mm,“R4.5”表示铆钉长度为4.5 mm;铆钉采用高硬度的合金钢制作,其钉头直径dw=7.6 mm,钉管直径d=5.3 mm,硬度采用洛氏硬度计测量,硬度等级HRC 在40~46。 表1 铆钉和模具参数 Table 1 Parameters of rivet and mold 图4 铆钉和底模示意图 Fig.4 Schematic diagram of rivet and the bottom die 自冲铆接的抗剪性能试验在型号为Zwick 的拉伸实验机(最大拉伸力为100 kN)上进行,采用位移控制的单调加载,加载度为3 mm/min[16]。试验时采集荷载-相对位移曲线数据并观察破坏过程,接头相对位移由配套的自动引伸计测量,测量标距为100 mm。 参考《金属材料拉伸试验:室温试验方法》(GB/T 228.1―2010)[23]中的规定,五种不同厚度的镀锌钢板各取样三组,材料性能试验测试结果的平均值见表2。由表2 可知,各类钢板的强屈比均大于1.2,且伸长率不小于10%,说明所采用钢板的材料符合延性要求。 表2 镀锌钢板材料特性 Table 2 Material properties of galvanized steel sheets 考虑钢板厚度、厚度比、铆钉长度因素的自冲铆接试件在剪切作用下的主要破坏模式可归纳如下三种:I. 铆钉腿拔出下层钢板(见图5(a));II. 铆钉头剪脱上层钢板(见图5(b));III. 铆钉腿倾斜拔出下层钢板并伴随铆钉头局部剪脱上层钢板,即I 和II 的组合(见图5(c))。 图5 自冲铆接的破坏模式 Fig.5 Failure modes of self-piercing rivet connections 图6 给出了破坏模式I 下试件的荷载-相对位移曲线。由图6 及试验现象可知:破坏模式I 下试件的破坏过程可以简化成三阶段:1) 弹性阶段:接头的上、下层钢板及内锁机构处于弹性阶段,其剪力主要靠铆钉头部与上层板孔壁承压及铆钉腿部与下层板材形成的内锁机构传递,荷载-相对位移呈线性增长的关系;2) 塑性阶段:弹性阶段后,接头的上层钢板端部开始翘曲变形,内锁机构发生塑性变形,荷载-相对位移曲线趋于平缓或者是荷载缓慢降低阶段,其斜率逐渐减小;3) 破坏阶段:上层钢板孔壁受铆钉头挤压发生轻微的塑性变形,铆钉轻微倾斜,内锁机构中的铆钉腿部逐渐被完全拔出,接头失效,荷载-相对位移曲线趋于急剧下降阶段。 图6 破坏模式I 下的荷载-相对位移曲线 Fig.6 Load-relative displacement curves under failure mode I 综上分析,自冲铆接在破坏模式I 下的破坏机理为:剪切作用下,上层钢板的孔壁承压,钉头处的弯矩使上层钢板的板端发生翘曲变形,下层钢板中的内锁机构剪切破坏;当内锁机构的受剪能力小于上层钢板孔壁的承压能力时,内锁机构失效。 图7 给出了破坏模式II 下试件的荷载-相对位移曲线。由图7 及试验现象可知:破坏模式II 下试件的破坏过程可以简化成四阶段:1) 弹性阶段:与上述破坏模式I 类似;2) 弹塑性阶段:接头的上层钢板孔壁局部挤压变形,钢板强度进入强化阶段,内锁机构仍处于弹性,荷载-相对位移呈非线性增长的关系,其斜率逐渐减小;3) 塑性阶段:铆钉头继续挤压上层钢板,铆钉孔迅速扩张,铆钉与钢板间产生较大的相对滑移,钢板强度进入下降段,内锁机构进入弹塑性,荷载-相对位移曲线趋于平缓或者是荷载缓慢降低阶段;4) 破坏阶段:铆钉头部进一步挤压上层钢板孔壁,直至孔壁发生挤压撕裂,铆钉头部完全脱离上层板材,此时,内锁机构处于塑性阶段,荷载-相对位移曲线趋于急剧下降阶段。 综上分析,自冲铆接在破坏模式II 下的破坏机理为:剪切作用下,铆钉受剪,上层钢板的孔壁承压,下层钢板中的内锁机构处于塑性,当上层钢板孔壁的承压能力小于内锁机构的受剪能力时,上层钢板的铆孔发生挤压撕裂破坏,铆钉头完全剪脱上层钢板。 图7 破坏模式II 下的荷载-相对位移曲线 Fig.7 Load-relative displacement curve under failure mode II 图8 给出了破坏模式III 下试件的荷载-相对位移曲线。由图8 及试验现象可知:破坏模式III 下试件的破坏过程可以简化成四阶段:1) 弹性阶段:与上述破坏模式I 类似;2) 弹塑性阶段:弹性阶段后,接头的上层钢板开始翘曲变形,铆钉逐渐倾斜导致内锁机构受拉剪共同作用,上层板孔壁及内锁机构发生弹塑性变形,荷载-相对位移呈非线性增长的关系,其斜率逐渐减小;3) 塑性阶段:铆钉继续倾斜,上层钢板孔壁的塑性变形增大且板端翘曲加剧,钢板强度进入强化阶段,内锁机构受拉侧开始失效,铆钉腿部逐渐被拔出,荷载-相对位移曲线趋于平缓或者是荷载缓慢降低阶段;4) 破坏阶段:上层钢板孔壁的挤压变形加剧,铆钉倾斜程度增加,铆钉腿部完全拔出下层钢板,接头失效,荷载-相对位移曲线趋于急剧下降阶段。 图8 破坏模式III 下的荷载-相对位移曲线 Fig.8 Load-relative displacement curves under failure mode III 综上分析,自冲铆接在破坏模式III 下的破坏机理为:铆接接头在剪切作用下,上层钢板的孔壁发生严重的承压变形,钉头处的弯矩使上层钢板的板端发生翘曲变形,铆钉倾斜使下层钢板中的内锁机构受拉剪共同作用;当内锁机构的抗拉剪能力接近上层钢板孔壁的承压能力时,上层钢板承压破坏,内锁机构拉剪失效,铆钉腿完全拔出下层钢板。 每组试件重复试验3 个试样,试验结果取其平均值,所有试件的受剪承载力及破坏模式见表3。 由表3 中的试验结果可知:下层钢板厚度一定时,钢板厚度比是影响自冲铆接破坏模式的关键因素。当厚度比(下层板厚度t2与上层板厚度t1之比)=1时,试件发生铆钉腿拔出下层钢板破坏(破坏模式I);当厚度比≥1.5 时,试件发生铆钉头剪脱上层钢板破坏(破坏模式II);当厚度比>1 且<1.5 时,试件发生铆钉腿倾斜拔出下层钢板并伴随铆钉头局部剪脱上层钢板的组合破坏(破坏模式III)。等厚钢板连接时(板厚比=1),随着钢板厚度的增加,试件均为发生铆钉腿拔出下层钢板破坏(破坏模式I),钢板厚度对自冲铆接破坏模式的影响较小。相同厚度钢板连接时,随着铆钉长度的变化,试件的破坏模式均为铆钉腿拔出下层钢板,铆钉长度对自冲铆接破坏模式的影响较小。 表3 自冲铆接的试验结果 Table 3 Test results of SPR joints 图9 给出了不同破坏模式下自冲铆接的受剪性能指标与钢板厚度比的关系。由图9(a)可知,不同板厚比区间下,钢板厚度对自冲铆接受剪承载力影响趋势的差别较大;当t2/t1=1 时,自冲铆接的受剪承载力随钢板厚度的增加基本呈线性增加,说明在铆钉腿拔出下层钢板的破坏模式下,其受剪承载力由下层钢板中的内锁机构的受剪能力决定;当t2/t1≥1.5 时,其受剪承载力随上层钢板厚度的增加而增加,说明在铆钉头剪脱上层钢板的破坏模式下,其受剪承载力由上层较薄钢板孔壁与铆钉头间的承压能力决定;当1 由图9(b)可知,自冲铆接的受剪刚度均随钢板组合厚度的增加而增加,且三种破坏模式下的趋势基本一致。钢板组合厚度是影响自冲铆接受剪刚度的关键因素,而钢板厚度比对其抗剪刚度影响较小;当钢板厚度达到2 mm 时,由于铆钉的直径偏小引起铆钉被剪断,从而使得其受剪刚度急剧降低;相同钢板组合厚度下,自冲铆接发生铆钉腿拔出下层钢板破坏时的刚度较大,而发生铆钉头剪脱上层钢板破坏时的刚度较低。 由图9(c)可知,钢板厚度比在=1、>1 且<1.5、≥1.5 三种区间下,试件的极限位移均值分别为3.124 mm、2.191 mm、5.208 mm,说明自冲铆接发生铆钉头剪脱上层钢板的破坏时,其变形能力相对较高。当t2/t1=1 时,自冲铆接的变形能力随钢板厚度的增加基本呈线性增加,当钢板厚度达到2 mm时,增速减缓;当1 综上分析,钢板厚度比是影响自冲铆接受剪性能的关键因素,且不同的板厚比区间对应不同的破坏模式。当t2/t1=1 时,自冲铆接的破坏模式为铆钉腿拔出下层钢板,其变形能力较小且属于脆性破坏;其受剪承载力、刚度、变形能力及延性随钢板组合厚度的增加基本呈线性增加的趋势;当t2/t1≥1.5 时,自冲铆接的破坏模式为铆钉头剪脱上层钢板,其变形能力较大且属于延性破坏,其受剪承载力随上层钢板厚度的增加而增加,而与钢板组合厚度无关,其抗剪刚度随钢板组合厚度的增加而增加,而与钢板厚度比无关,其变形能力和延性随板厚比的增加而增加,而钢板组合厚度影响较小;当1 图9 自冲铆接的受剪性能指标与板厚比间的关系 Fig.9 Relationship between shear property index and thickness ratio for SPR connections 为考察铆钉长度对自冲铆接受剪性能的影响,图10给出了自冲铆接的受剪性能指标与铆钉长度的关系。由图10 可知:对于相同板厚组合(1.5 mm+1.5 mm)的自冲铆接试件,铆钉长度分别为5 mm、5.5 mm、6 mm、6.5 mm、7 mm时,其抗剪承载力均值分别为6.81 kN、7.28 kN、7.40 kN、7.23 kN、7.33 kN,最大值与最小值相差13%;其抗剪刚度均值分别为22.49 kN/mm、25.10 kN/mm、28.78 kN/mm、26.22 kN/mm、22.58 kN/mm,最大值与最小值相差28%;抗剪承载力、刚度随着铆钉长度增加而先增加后减小,极限位移和延性系数随铆钉长度的增加而增加,但钉长超过6 mm后延性系数的增速减缓。综上,对于相同板厚组合的自冲铆接,铆钉长度对其抗剪性能的影响显著,从抗剪承载力、刚度、延性的影响规律分析可知:铆钉存在较优长度。 从自冲铆接的成型机理与破坏机理来分析上述规律可知:铆钉长度为5 mm、5.5 mm时,铆钉长度相对过小,铆钉张开不充分,内锁长度较小且成型不完善,使其抗剪能力远小于上层板孔壁的承压能力,内锁机构过早失效导致该类试件的受剪性能较差;铆钉长度为6 mm时,铆钉长度相对适宜,铆钉张开较充分,内锁长度及残余底厚较大,内锁机构的抗剪能力与上层钢板的孔壁承压能力接近,从成型质量的检测标准判断该铆接的质量较优,且该破坏机理能充分发挥内锁机构及板材的性能,故该类试件的抗剪性能较优;铆钉长度为6.5 mm、7 mm时,铆钉长度过大导致残余底厚较小,从成型质量的检测标准来判断该类锁铆接头的成型质量较差,受较小力时接头底部就会出现裂纹和穿透现象,内锁机构过早损伤导致该类试件的抗剪性能较差。因此,铆钉长度是影响自冲铆接受剪性能的重要参 数。为确定冷弯薄壁型钢结构中常见钢板组合厚度下铆钉的较优长度,综合本次试验及参考文献[9,13,24―25]确定的铆钉长度,拟合出了钢板组合厚度与较优铆钉长度间的关系如图11所示。 基于图11 拟合成的钢板组合厚度与铆钉长度间的经验公式如下: 式中:L/mm为铆钉长度;t1/mm为上层钢板的厚度;t2/mm 为下层钢板的厚度。该式仅适用于0.8 mm~2.5 mm厚的薄壁钢板,且1.6≤t1+t2≤5。 图10 自冲铆接的受剪性能指标与铆钉长度的关系 Fig.10 Relationship between shear property index and rivet length for SPR connections 图11 钢板组合厚度与铆钉长度间的关系 Fig.11 Relationship between combined thickness of steel sheets and rivet length 当t2/t1= 1时: 当t2/t1≥ 1.5时: 当 1 <t2/t1< 1.5时:Fs取上述情况的较小值。 式中:Fs/N 为铆钉连接受剪承载力计算值;α1、α2为计算系数,由所有试件的试验结果取平均值标定,计算系数的确定方法与结果如表5 所示,当t2/t1=1 时,α1=3.52,当t2/t1≥1.5 时,α2=2.58;fy1/(N/mm2)、fy1/(N/mm2)分别为铆钉头侧、铆钉尾侧钢板的抗拉强度设计值;d/mm、dw/mm 分别为铆钉的钉管直径与钉头直径;t1/mm、t2/mm 分别为铆钉头侧、铆钉尾侧钢板的厚度;L为铆钉长度,由式(20)确定。 表4 计算方法对比 Table 4 Comparison of calculation methods 表5 计算系数确定方法与结果 Table 5 Definition method and results for calculation coefficients 然而,本文提出的承载力计算式(21)、式(22)存在一定的适用范围:1) 被连接板材为薄壁钢板,且其屈服强度范围为235 MPa~280 MPa;2) 薄钢板的厚度应控制在0.8 mm~2.0 mm,且其组合厚度不宜大于4 mm;3) 被连接钢板的组合方式宜为较薄板位于钉头侧且较厚板位于钉尾侧;4) 铆钉的钉头直径和钉管直径分别不宜小于7.6 mm 和5.3 mm,且其洛氏硬度等级应在40-46 HRC。 图12 和表4 给出了五国规范、Haque、Yan 及本文提出的八种计算方法的比值(计算值与试验值之比)对比情况。由表4 可知:本文提出的自冲铆接受剪承载力计算方法,其计算值与试验值之比的均值和变异系数分别为0.99、0.07。由图12 可知:与现有五国规范中自攻螺钉的计算方法相比,北美规范的计算值与试验值最为接近,日本规范的计算方法最为保守,而本文基于不同破坏模式提出的自冲铆接受剪承载力计算方法最为精确合理,其计算值的稳定性最高;与现有研究中的自冲铆接受剪强度预测方法相比,Haque 和Yan 的计算方法精度较高,但其覆盖的破坏模式不全,而本文提出计算方法能考虑更全面的破坏模式。 图12 八种自冲铆接承载力计算方法对比 Fig.12 Comparison of eight kinds of calculation methods for strengths of SPR joints (1) 薄壁钢板自冲铆接在剪切荷载下的破坏模式为:铆钉腿拔出下层钢板(破坏模式I)、铆钉头剪脱上层钢板(破坏模式II)、铆钉腿倾斜拔出下层钢板并伴随铆钉头局部剪脱上层钢板(破坏模式III)。 (2) 钢板厚度比(t2/t1)是影响自冲铆接破坏机理的关键因素。t2/t1=1 时,破坏模式I 的破坏机理为内锁机构失效,受剪承载力由下层钢板中内锁机构的抗剪能力决定;t2/t1≥1.5 时,破坏模式II 的破坏机理为上层钢板的承压破坏,受剪承载力由上层钢板孔壁与铆钉头间的承压能力决定;1 (3) 钢板厚度是影响自冲铆接受剪性能的主要因素。t2/t1<1.5 时,自冲铆接的受剪承载力、刚度、变形能力及延性随钢板组合厚度的增加基本呈线性增加;t2/t1≥1.5 时,受剪承载力随上层钢板厚度的增加而增加,抗剪刚度随钢板组合厚度的增加而增加,变形能力和延性随板厚比的增加而增加。 (4) 钢板组合厚度一定时,铆钉长度对自冲铆接的抗剪性能影响较大。受剪承载力、刚度随着铆钉长度增加的趋势为先增加后减小,极限位移和延性系数随铆钉长度的增加而增加,但铆钉长度过大后延性系数的增速减缓。 (5) 对于特定钢板组合厚度的自冲铆接,铆钉存在较优长度;提出的钢板组合厚度与铆钉较优长度间的经验公式能快速确定冷弯型钢结构中常见组合厚度钢板所需的铆钉长度。 (6) 基于试验结果及理论分析,提出了自冲铆接的受剪承载力计算方法。与现有规范及研究者的计算方法相比,该方法能考虑更全面的破坏模式,且其计算值精度更高、稳定性更好。1.2 文献Haque 与Yan 的受剪强度预测方法
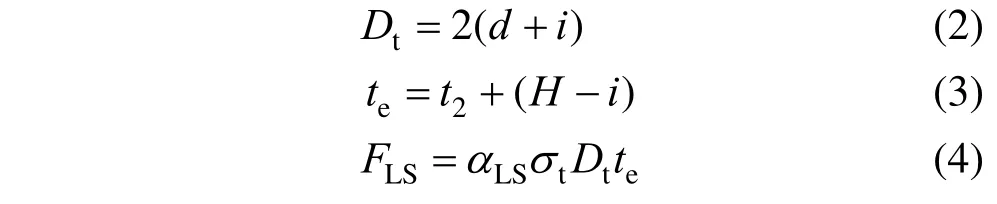
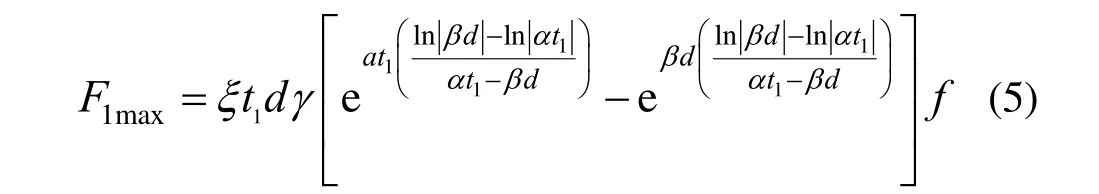
1.3 国内外自攻螺钉连接受剪设计计算方法


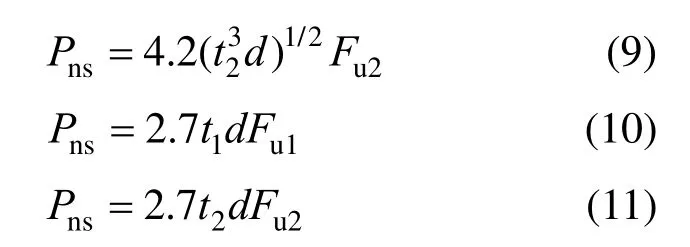



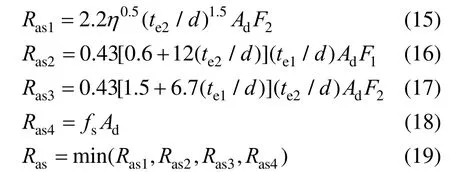
2 试验概况
2.1 试件设计
2.2 加载装置和加载制度
2.3 材料性能试验
3 试验结果与分析
3.1 试件破坏模式

3.2 荷载-位移曲线及破坏机理分析


4 影响因素分析
4.1 钢板厚度、厚度比、铆钉长度对自冲铆接破坏模式的影响
4.2 钢板厚度比对自冲铆接受剪性能的影响

4.3 铆钉长度对自冲铆接受剪性能的影响
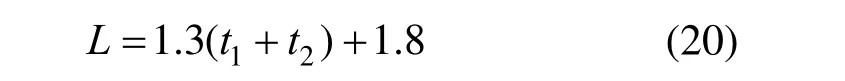

5 薄壁钢板自冲铆接受剪承载力 计算方法
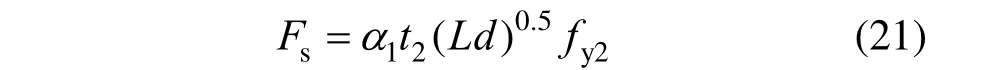


6 结论
