钢筋活性粉末混凝土简支梁受弯力学 性能试验与计算
2020-06-01李海艳张博扬李金书
李海艳,张博扬,李金书
(1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,河北,石家庄 050043; 2.石家庄铁道大学工程力学系,河北,石家庄 050043)
活性粉末混凝土(Reactive Powder Concrete,RPC)是一种拥有超高强度、低脆性、优异耐久性并且使用前景非常广阔的超高强度混凝土[1],它的主要组分为水泥、石英砂、硅灰、高效减水剂、矿渣以及钢纤维。RPC 组分与力学性能均与普通混凝土(OC)不同,因此,其构件承载力计算公式必然不同于普通混凝土。此外,随着各国在土木、市政等工程领域对RPC 材料的研究[2-3]及推广应用[4-6],对RPC 构件开展力学性能研究显得尤为重要。
目前,针对RPC 材料与构件力学性能方面取得了一定研究成果。RPC 材料性能方面,西安建筑科技大学邓明科等[7]通过RPC抗压强度试验论证了石英粉、粉煤灰、纤维掺量对RPC 强度的影响。Hassan等[8]试验研究了养护制度对试件轴心抗拉强度的影响,认为进行2 天90℃高温养护、7 天常温养护可接近RPC 极限强度。RPC 构件受力性能方面,杨克家等[9]对RPC 空截面受压构件进行轴压破坏试验,并对其进行了数值模拟。哈尔滨工业大学郑文忠等[10-11]得到了小尺寸钢筋RPC 简支梁正截面承载力及刚度计算公式。但有关RPC 简支梁抗弯性 能的试验数据还相对较少,所以对室温下钢筋RPC简支梁受弯性能开展足尺试验研究具有重要的 意义。
制作4 根钢筋RPC 简支试验梁,并对其进行受弯试验,得到试验梁极限承载力与跨中荷载-位移曲线,考察试验梁的受力性能与破坏模式;通过计算推导得到RPC 梁截面抵抗矩塑性影响系数,进而得到相应的开裂弯矩计算公式和考虑拉区影响的钢筋RPC 简支梁正截面抗弯承载力计算公式。
1 试验概况
1.1 原材料与配合比
试验选用P.O42.5 级普通硅酸盐水泥;SiO2质量分数90%、比表面积20000 m2/kg 的硅灰;比表面积55000 m2/kg 的S95 型矿渣粉;聚羧酸减水剂;40 目~70 目和70 目~140 目石英砂;平直钢纤维,长度为13 mm,长径比为59.1[12];聚丙烯纤维长度为14 mm~16 mm,直径18 μm~48 μm,比重0.91;钢筋统一采用HRB400 级钢筋。
本试验用RPC 基准配合比为:水泥∶硅灰∶矿渣∶石英砂∶减水剂∶水=1∶0.3∶0.15∶1.2∶0.058∶0.26。在此基准配比基础上分别单掺钢纤维体积率2%或混掺钢纤维体积率2%、聚丙烯纤维体积率0.2%得到本文用RPC 配合比。试验用RPC 材料力学指标如表1 所示,其中峰值拉应变对于混掺与单掺纤维两种RPC 基本一致,所以取值相同。

表1 RPC 材料力学指标 Table 1 RPC material mechanical properties
1.2 试件设计
试验设计了4 根RPC 简支试验梁,试验梁的设计截面尺寸均为250 mm×400 mm,计算跨度为 4.5 m,为防止两端的锚固破坏,两边各预留 0.2 m[14],试验梁总长度为4.9 m。纵筋、箍筋、截面压区架立筋均采用HRB400 级钢筋。试验梁的配筋示意图如图1 所示,RPC 试验梁参数如表2 所示。其中L1、L2、L3 混掺聚丙烯纤维和钢纤维,L4 只掺钢纤维。
1.3 试件养护
RPC 试验梁制作成梁后需要进行高温蒸汽养护,其中90℃养护3 天,120℃养护2 天[15]。钢筋绑扎图以及成梁图如下图2、图3 所示。
1.4 试验方案
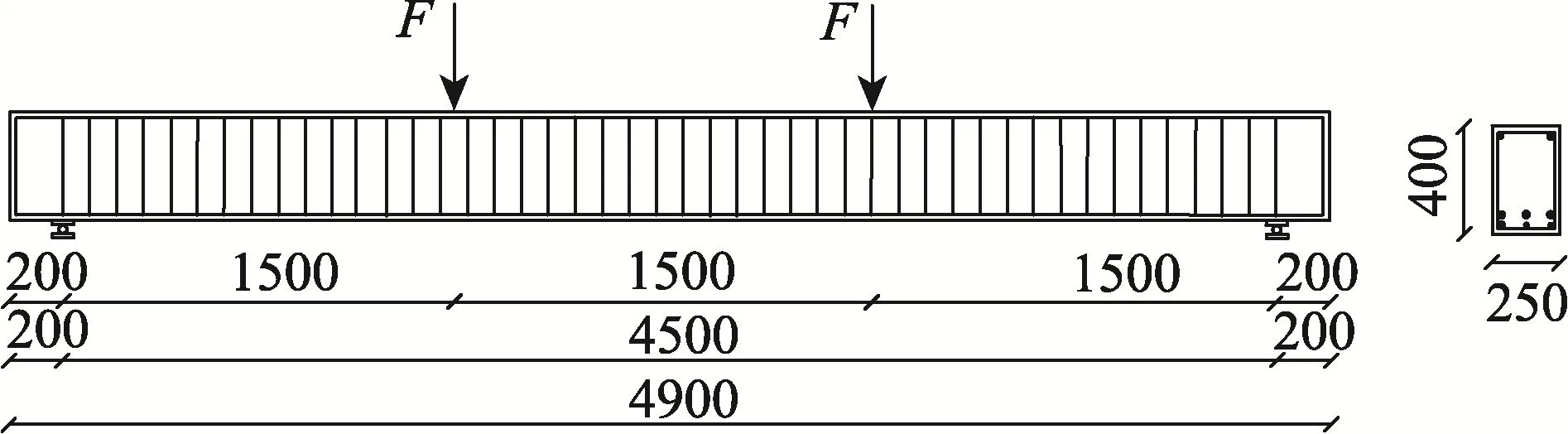
图1 RPC 梁配筋 Fig.1 RPC beam reinforcement

表2 RPC 试验梁参数表 Table 2 RPC beams information

图2 钢筋绑扎 Fig.2 Reinforcement banding

图3 制备成梁 Fig.3 Preparation of beam
试验采取三分点加载,在梁的左右两个加载点、支座以及跨中最大位移处设置位移计,测量跨 中挠度。在跨中侧面沿梁高方向均匀粘贴5 组应变片(见图4(a)),在梁上表面沿横向粘贴3 组应变片,测定应变。将钢筋应变片在成梁时贴至底部纵筋纯弯段,测定钢筋应变。试验前进行预加载,预加载范围不超过试验梁预估计算荷载的5%,检查试验设备是否完好,在检查无误后卸载,开始进行加载。
试验采用分级加载制度,在混凝土开裂前,每级加载值为预估开裂荷载的10%;达到开裂预估值的75%时,每级加载变更为5 kN;当试验梁开裂后,每级加载增加至10 kN;当试验梁达到极限预估值的90%时,再次变更每级加载数值为5 kN,直至试验梁破坏,宣布试验结束。图4 为四点抗弯试验图。

图4 抗弯试验加载 Fig.4 Bending test loading
2 试验结果与分析
2.1 试验现象
4 根试验梁的破坏形式均为适筋破坏,纯弯段受拉钢筋最先达到屈服,然后受压区混凝土被压碎,宣告试验结束;L1 于160 N 时首次出现裂 缝,720 kN 时裂纹扩展,840 kN 受压区破坏,宣告试验结束。L2 在荷载100 kN 时出现裂缝,加载至380 kN 时有足够长的屈服阶段后,从梁体纯弯段靠左处发生断裂。L3 在荷载为145 kN 时发生开裂,加载至565 kN 裂缝加宽,至640 kN 时受压区混凝土破坏,最终跨中位移为73 mm。L4 为不掺聚丙烯试验梁,开裂弯矩为155 kN,加载至660 kN时受压区破坏,各试验梁破坏形态见图5,裂缝展开图见图6。

图5 RPC 梁破坏形态 Fig.5 Failure modes of RPC beams
试验梁两侧摆放东西朝向,故试验梁分为南北两面,L1 共83 条裂缝,其中扩展到1 mm 以上的8条,在纯弯段外出现大量受剪破坏裂纹;L2 一共60 条裂缝,其中1 mm 以上共14 条;L3 共48 条裂缝,1 mm 以上共12 条,L4 一共68 条裂缝,其中1 mm 以上为20 条。

图6 各试验梁裂缝分布图 Fig.6 Crack distributions of test beams
2.2 荷载-挠度曲线
试验实测的跨中荷载-位移曲线如图7 所示,由图可知,对于L1、L2、L3、L4,跨中荷载-位移曲线大致可分为3 个阶段。第1 阶段为混凝土开裂前,此阶段跨中荷载-位移曲线呈直线,试件的截面刚度较大;第2 阶段为混凝土开裂至受拉钢筋屈服,由于钢纤维具有一定的结拉作用,此阶段曲线近乎为一次曲线;第3 阶段为钢筋屈服到受压区混凝土被压碎,在此阶段曲线的斜率不断下降,荷载增加幅度小,变形较大,直至受压区混凝土被压碎,达到极限承载力试验梁受弯破坏。

图7 试件跨中荷载-位移曲线 Fig.7 Specimen load - mid-span deflection curves
将4 根试验梁跨中荷载-位移曲线汇总于图8。由图可知,随着配筋率的提高,RPC 简支梁极限承载力逐渐增大,且含有聚丙烯与不含聚丙烯的L3与L4 极限承载力相差较小,跨中荷载-位移曲线无明显差别。钢筋屈服后,荷载增加幅度较小的情况下,位移迅速增大,由此可见相较于普通混凝土,RPC 具有较好的延性。
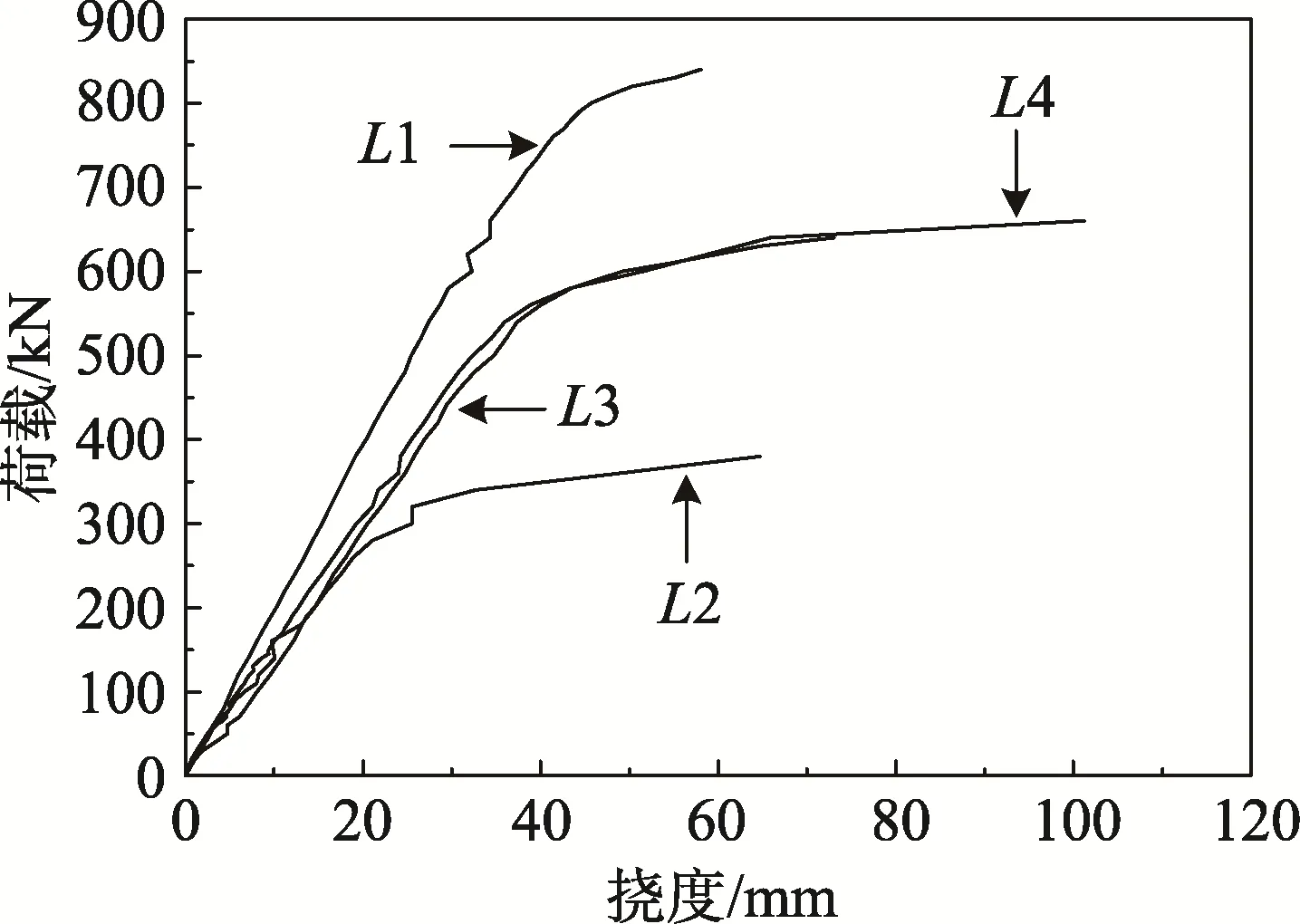
图8 试件荷载-跨中挠度曲线汇总图 Fig.8 Specimen load-mid-span deflection curves summary
4 根试验梁试验数据汇总于表3,由表3 可以看出,开裂弯矩与极限弯矩随着配筋率的增大而增大。配筋率相同、掺钢纤维率相同,不掺聚丙烯纤维的L4 与混掺聚丙烯纤维的L3 相比,开裂荷载与极限承载力均略微偏高,结合课题组前期研究成 果[16]可见,聚丙烯纤维的掺入对常温RPC 简支梁承载力略有削弱,但削弱有限。
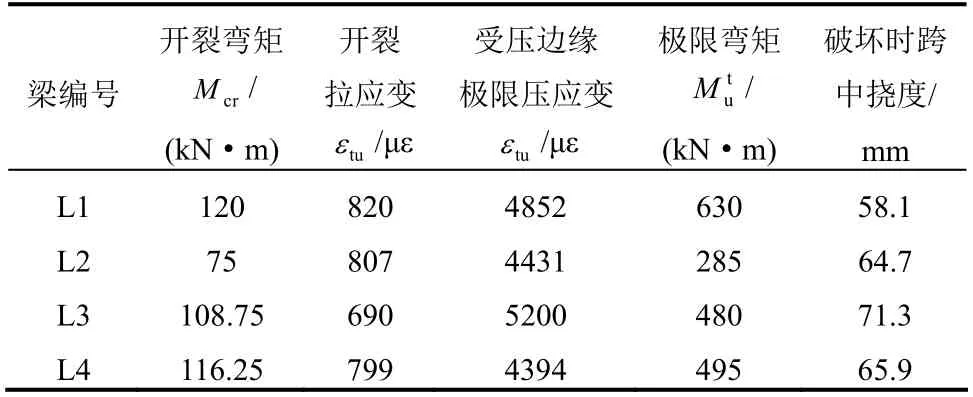
表3 试验数据汇总 Table 3 Experimental data sheet
由表3 可知,本试验测得RPC 受压边缘极限压应变为4394 με~5200 με,受拉区边缘RPC 开裂应变为690 με~820 με,《钢筋混凝土结构设计规范》(GB 50010―2010)中普通混凝土的极限压应变3300 με、开裂应变80 με~120 με,可见RPC 的取值远大于普通混凝土的取值,RPC 延性和韧性均优于普通混凝土。
3 材料力学性能
3.1 RPC 力学性能
钢筋RPC 梁正截面受弯承载力分析时选用文献[9]中的受压与受拉应力-应变关系方程,表达式分别如式(1)、式(2)所示:
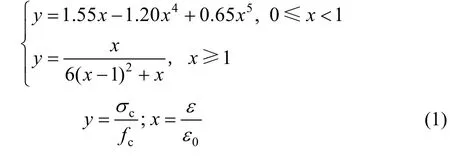
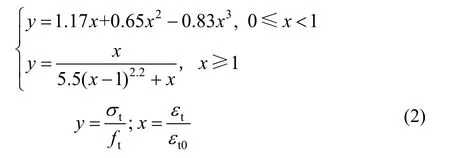
式中:ε为RPC 压应变;0ε为RPC 峰值压应变;tε为RPC 拉应变;t0ε为RPC 峰值拉应变;cσ为RPC压应力;tσ为RPC 拉应力;cf为RPC 抗压强度;
ft为RPC 抗拉强度。
3.2 钢筋力学性能
试验梁的纵筋、箍筋、截面压区架立筋均采用HRB400 级钢筋。
为了简化计算,在混凝土受弯构件计算时钢筋使用理想弹塑性应力的模型,在钢筋设计强度范围内,钢筋的应力等于应变与弹性模量的乘积。即:

式中:sσ为钢筋应力;sA为纵向受拉钢筋的截面面积;sE为钢筋弹性模量;fy为纵向受拉钢筋屈服强度。
3.3 受拉区RPC 影响
普通混凝土受弯构件计算时,一般不考虑混凝土拉区拉应力的贡献,但由于RPC 具有较高的抗拉强度(见表1),且在开裂后,由于钢纤维的结拉作用,仍然有拉应力的存在,所以RPC 受弯构件计算时拉区拉应力作用不可忽略。
为便于计算模型的建立,试验采用平截面假定。从严格意义上讲,破坏局部截面平截面假定已经不再适用,但是考虑到混凝土构件的破坏是在一定区间长度内,平截面假定在一定程度上适用于RPC 梁的受弯构件计算。
4 钢筋RPC 简支梁计算方法
4.1 开裂弯矩计算
4.1.1 截面抵抗矩塑性影响系数计算
混凝土梁在弹性工作阶段受拉区应变近乎呈线性分布,受拉区应力分布为曲线型。为计算简便将模型进行简化,受拉区的应变图形简化为三角形,受拉区应力图形简化为梯形,如图9 所示。根据受压区合力与钢筋合力进行力的平衡运算可得到受拉区边缘拉应力为应力最大值的10%[10]。由简化的应力图形,通过受拉区峰值拉应变与受拉区开裂边缘应变的比值得到应力最大值的位置为:




表7 试验梁承载力试验值与计算值比较 /(kN·m) Table 7 Comparison of calculated and test values of test beams
4.2.4 界限相对受压区高度及配筋率限值
通过平截面假定和定义可得界限相对受压区高度:

其中,εcu为RPC 受压极限应变,混凝土梁的破坏类型可以根据ξb进行判断,如果ξ>ξb则为超筋破坏,钢筋无明显屈服点,如果ξ<ξb则属于适筋破坏,钢筋有明显的屈服点,如果ξ=ξb则为界限破坏,ξb是配筋是否合理运用的一个标准。将本文试验梁的具体参数代入式(25),得到最大配筋率为13.6%。

根据《钢筋混凝土结构设计规范》(GB 50010―2010)的相关规定,纵向受力钢筋的最小配筋率minρ为0.2%与0.45ft/fy中的较大值,经计算得最小配筋率为1.01%。
4.3 刚度计算
由于钢纤维的拉结作用,相较于普通混凝土而言,RPC 的抗拉强度不可忽略,所以RPC 梁受弯时,弯矩由受拉区RPC 与钢筋同时承担,因此采用文献[10]推导的刚度计算公式,具体如下:

式中:M为截面所承担的弯矩;MT为截面拉区RPC的拉应力合力T对压区RPC 合力作用点的力矩;为截面拉区RPC 的拉应力合力T对钢筋拉力作用点的力矩;Ms为纵向向钢筋所承担的弯;Mc为压区RPC 所承担的弯矩;ω为压区RPC 应力图形丰满系数;ψ为裂缝间受拉钢筋应变不均匀系数;ξ受压区边缘平均应变综合系数。
四点弯曲试验的挠度计算公式为:

试验梁挠度计算值与试验值对比见表8 所示,通过表8 可知,计算值与实测值的比值均值为1.03,式(27)用于钢筋RPC 简支梁挠度计算具有较高的精度。L3 与L4 挠度比较接近,可见是否含有聚丙烯对梁的变形影响较小。

表8 挠度计算值与试验值对比表 Table 8 Test and calculated data of deflection
5 结论
本文通过试验,研究了4 根钢筋RPC 简支梁的受力性能与破坏模式,得出如下结论:
(1) 4 根简支梁的破坏形式均为适筋破坏,RPC的受压边缘极限压应变与开裂应变均远大于普通混凝土,具有比普通混凝土更优越的延性和韧性。
(2) 结合RPC 材料属性和试验结果,推导得到了RPC 截面抵抗矩塑性影响系数mγ在一定配筋率范围下的拟合公式,进而推得了开裂弯矩的计算公式,公式计算值与试验值吻合较好。
(3) 由于钢纤维的掺入,钢筋RPC 简支梁正截面受弯承载力计算时必须考虑拉区拉应力的影响,基于试验数据与理论推导,得到适筋梁受拉区拉应力贡献系数k可取为0.3,并据此提出了正截面受弯承载力计算公式,且公式计算值与试验值吻合较好,给出钢筋RPC 简支梁适筋配筋率建议取值范围为1.01%~13.6%。
(4) 结合本文试验数据,验证了文献[10]中刚度计算公式的正确性。此外,本试验还发现,聚丙烯纤维的掺入对常温RPC 简支梁承载力略有削弱,但削弱有限。
