弹性膜结构几何非线性分析的刚体准则法

陈朝晖，杨 帅，杨永斌,3

(1. 重庆大学土木工程学院，重庆 400045；2. 山地城镇建设与新技术教育部重点实验室(重庆大学)，重庆 400045； 3. 国立云林科技大学营建工程系，台湾 64002)

膜结构具有轻盈、便于覆盖大跨屋盖、造型多变以及可以预制等许多显著优点，近30 年得到快速发展，在工程实践中发挥了重要作用。由于膜结构面外刚度很小，即使在较小横向荷载下，也易发生较大挠曲变形，因而，膜结构通常通过较大变形来抵抗荷载，具有明显几何非线性特性。

Masahisa 等[1]提出了张拉结构的非线性分析方法，利用更新拉格朗日列式以考虑膜结构的大变形影响。Tabarrok 和Qin[2]采用非线性有限元方法对膜、索和框架组成的组合张拉结构进行找形与荷载分析，但所推导的膜单元为复杂的高阶单元，数值积分时需要较多插值点，效率与精度无法兼顾。Noguchi 等[3]利用无网格伽辽金法(element-free Galerkin method，EFG)对空间膜结构进行几何非线性分析，突破了传统有限元分析中单元网格的限制，取得了较为满意的结果，但在基函数和影响域方面，未明确最佳顺序和大小，影响了该方法的稳定性和通用性。Tsiatas 等[4]提出了空间任意形状薄膜大挠度分析方法，利用变分法推导了新的控制微分方程，并采用模拟方程法(the analogue equation method，AEM)对微分方程进行直接积分求解，即在相同的边界条件下，用三个非耦合的等效线性平面膜方程替换三个耦合的变系数非线性偏微分方程。该方法精度较高，计算效率高于其他数值方法，一般情况下对于预应力膜，解的收敛性较好，但随着预应力的减小，收敛性变差。王震[5]和赵阳等[6]基于向量式有限元法(the vector form intrinsic finite element method，VFIFEM)，推导了三角形常应变膜单元和四结点四边形等参膜单元，详细描述了变形坐标系下单元结点内力的求解方法，同时对四结点膜单元的位移模式和内力计算的数值积分等问题提出了合理可行的处理方法，有效模拟了空间膜结构大位移和大转动行为，但该方法计算效率与普通有限元法相比并无优势。

增量迭代法是结构非线性分析的通行方法，基本思想是将非线性过程在各荷载增量阶段线性化，该方法大致可分为三个阶段：增量预测阶段、单元结点力计算阶段和误差判断阶段。单元结点力与荷载之差通过迭代逐步减小。其中，单元结点力的计算决定了整个计算的精度。对于考虑大变形和大转动的单元，常见的各类几何刚度矩阵都存在不同程度的近似，在增量迭代过程中，如果这种近似造成了单元自身不平衡，所产生的误差是无法通过迭代消除的，甚至可能导致计算发散。解决方法之一是细分单元，但会极大降低计算效率。

为此，Yang 等[7－8]于1987 年提出了几何非线性分析的“刚体准则”，即发生刚体转动的单元，在初始状态下满足平衡条件的结点力，仅随单元转动而不会改变大小。Yang 等[9]运用虚功原理推导了满足上述刚体准则的杆系结构、板壳结构[10]等结构相应单元几何刚度矩阵，并基于更新的拉格朗日列式(Updated Languagian，简记作UL)，建立了与刚体准则相匹配的非线性增量迭代方法。这一思想方法，从根本上解决了大变形过程中单元的平衡问题，有效提高了收敛速度和精度。Yang 等[9]由此建立了一些列满足刚体准则的杆单元、平面及空间梁单元[8]和壳单元[10]，Yang 和Chen 等[11]结合塑性铰理论，将弹性几何非线性杆单元进一步推广到框架结构的弹塑性几何非线性分析中。所建立的单元几何刚度矩阵形式简洁，几何非线性分析简单明了。与现有非线性分析方法相比，计算效率优势显著[11－12]。

鉴于前述各膜单元的不足以及刚体准则在几何非线性分析中简明优美的出色表现，本文应用刚体准则，建立了一种新的适于工程应用的弹性非线性分析膜单元。该单元由满足刚体准则的空间杆单元和常规弹性膜单元构成，其中，膜单元的几何刚度矩阵由杆单元构成，弹性刚度矩阵则由平面应力单元构成。经验证，由此构成的空间膜单元和平面膜单元满足刚体准则，即弹性刚度矩阵和几何刚度矩阵在单元刚体位移上虚功为零。若干经典算例分析以及与已有分析方法的对比，验证了本文所建单元以及相应分析方法的精度及效率。

1 刚体准则的基本思想

如图1 所示刚体单元，在1C状态下保持平衡，当单元仅发生刚体位移运动到2C状态时，由于单元没有自然变形，不会产生新的结点力，仍应保持平衡。因此，单元结点力应为伴随力，即随单元一起运动至2C状态，大小不变，仅发生方向的改变。此即“刚体准则”[7]。

图1 发生刚体位移的初始平衡刚体单元 Fig.1 Rigid body motion of a rigid element with initial forces

对于发生大变形或大位移的单元，设在1C状态平衡，由1C状态至2C状态，单元将经历大变形或大位移，可将这一过程视为如下两个过程的叠加：单元先由1C至2C发生刚体位移，而后在2C状态下发生有限变形。在刚体位移阶段，1C状态平衡的单元结点力同单元一起转动而大小不变，在2C状态下仍然平衡；而后，再计算2C状态下的有限变形以及由变形引起的单元结点力增量。

对于大多数工程中的大变形和大转动问题，当增量步较小时，可以认为刚体位移占单元总的变形或位移的绝大部分，而有限变形仅占小部分。这样处理，物理概念明确清晰，将极大减小2C状态下的结点不平衡力，有效提高迭代计算的效率，即使产生变形描述的误差，也可以通过细分单元或减小步长来有效降低。

2 三角形空间膜单元

2.1 三角形空间膜单元的构造

如图 2 所示三结点三角形空间膜单元(Triangular space membrane element，简称TSME)，图中，OXYZ和Cxyz分别为结构整体坐标系，单元坐标系，其中x轴和y轴在单元平面内，z轴垂直于单元平面，坐标原点为单元形心C。设每个结点包含三个自由度，即两个面内平动自由度和一个面外平动自由度。结点i在单元坐标系下的坐标为(xi,yi,0)，ui、vi和wi分别为结点i沿x轴、y轴和z轴的位移，i=1,2,3。

结构的几何刚度矩阵本质上体现了由于结构几何形状的改变而产生的荷载势能，是荷载在结构变形上所做的虚功，因此，建立空间膜单元几何刚度矩阵的关键在于对膜单元整体变形的描述。根据前述刚体准则思想，可认为膜单元在变形过程中，其刚体位移对其整体变形的贡献较大，而单元的弹性变形贡献较小。进一步地，由三角形稳定性可知，若三角形三条边的位置和长度确定，三角形的形状及位置即可唯一确定。由此，可将三角形膜单元视为由三根空间杆件组成铰接三角形，并在中间张拉薄膜而成，杆件的材料与薄膜相同，如图3 所示。如此建立的空间膜单元的整体位形与位移即可由杆单元构成的空间铰接三角形确定，而膜单元的有限弹性变形可由内部张拉的薄膜变形确定。因此，本文所建空间膜单元的几何刚度矩阵可由杆件铰接三角形的几何刚度矩阵得到，弹性刚度矩阵则为内部张拉薄膜的弹性刚度矩阵，后者与通常的线性膜单元相同。以下即由空间杆单元几何刚度矩阵推导建立空间膜单元的几何刚度矩阵。

图2 三结点三角形空间膜单元 Fig.2 The TSME with three nodes

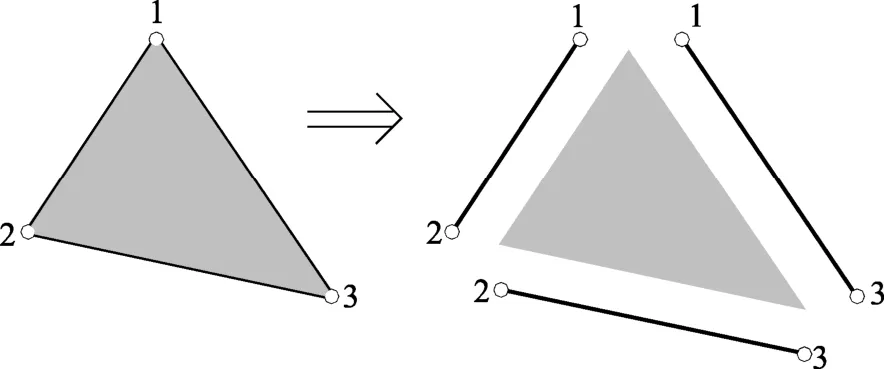
图3 三角形空间膜单元构成 Fig.3 Construction of TSME

2.2 三角形空间膜单元的几何刚度矩阵

单元坐标系下三角形空间膜单元的结点力如图4(a)所示，将其中的铰接三角形单元拆分为三个空间杆单元，相应杆端力如图4(b)所示。本文各物理量的左上标表示当前状态，左下标表示参考状态，则图中11xF表示在1C状态膜单元中结点1 沿x方向的结点力，表示在C1状态杆单元12 结点1 处沿x方向的杆端力，其余类似。

C1状态下三角形空间膜单元的结点力向量｛｝可记作：

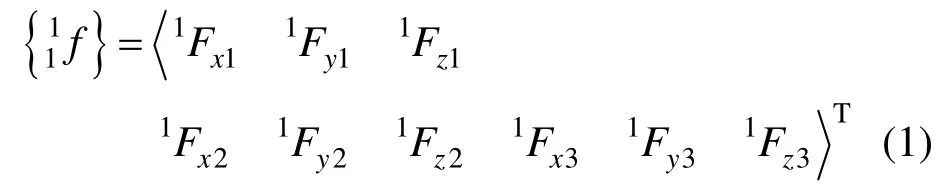
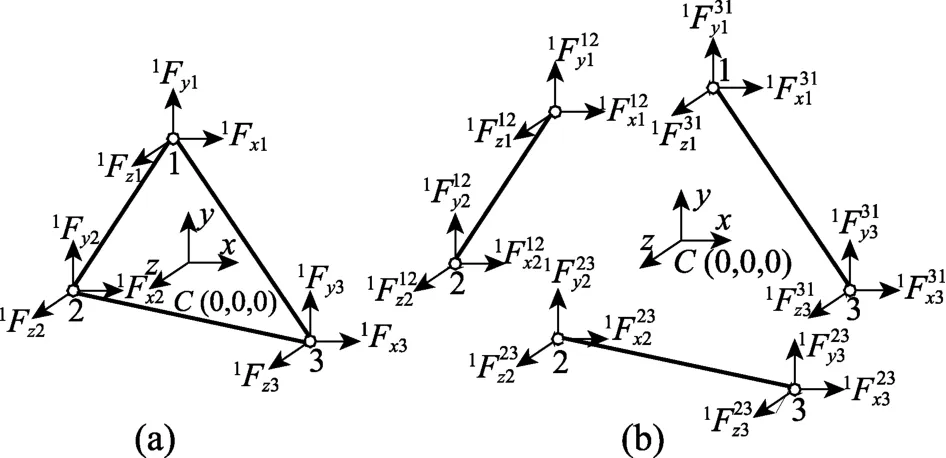
图4 三角形空间膜单元结点力和杆端力 Fig.4 The nodal and internal forces of TSME

膜单元与杆件需满足如下平衡条件：

三角形空间膜单元与杆单元在各结点上需满足平衡方程：

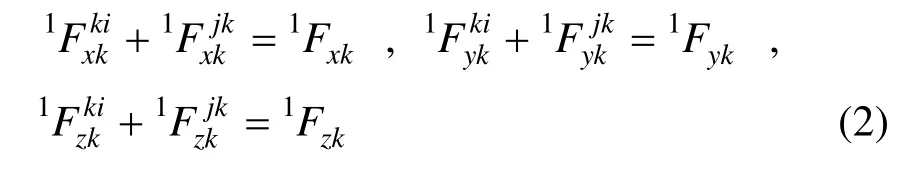
式中，右上标i,j,k分别用1,2,3 轮换，以下同此。

空间杆单元ij的杆端力需满足平衡方程：

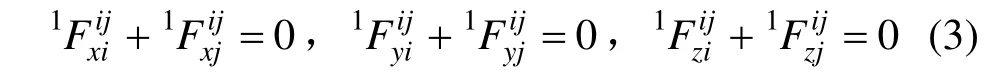
三角形空间膜单元的结点力需满足平衡方程：

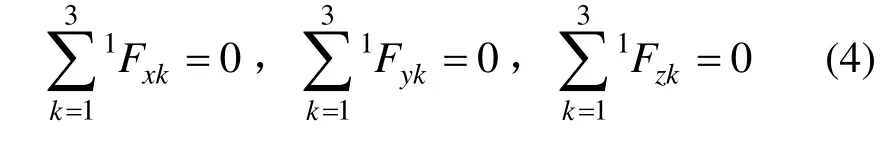
联立方程式(2)～式(4)，得到空间杆单元ij的杆端力为：

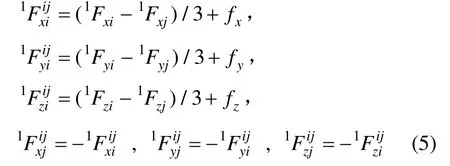
其中，xf、yf和zf是式(2)～式(4)求解过程中引入的待定常数，可令其为零。

由图4 可知，式(5)中空间杆单元的杆端力是相对于膜单元的单元坐标系。进一步地，需将其转换到各杆单元所在的局部坐标系下，如图5 所示，图中，、和是杆单元局部坐标轴。用｛｝和分别表示空间杆单元ij在膜单元的单元坐标系与杆单元局部坐标下的杆端力向量：

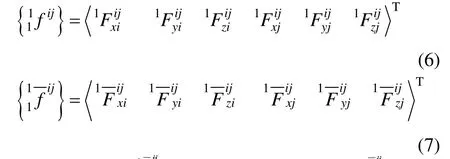
图5 局部坐标系下空间杆单元的杆端力 Fig.5 The internal force of 3D bar in local coordinate

两组向量之间有如下坐标变换关系：

其中，坐标转换矩阵 3D[ ]T具体如下：

式中，xij=xi-xj，yij=yi-yj，Lij为空间杆单元ij的长度。

将杆单元ij的几何刚度矩阵 [kg]3Dbar_ij从杆单元局部坐标系转换到三角形膜单元的单元坐标系，按照单元的结点自由度编码，“对号入座”叠加得到三角形空间膜单元的几何刚度矩阵 [kg]TSME：

其中：

2.3 三角形空间膜单元的弹性刚度矩阵

三角形空间膜单元的弹性刚度矩阵可由三角形平面应力单元的弹性刚度矩阵[13]修正得到。将三角形平面应力弹性刚度矩阵扩阶，即在平面弹性刚度矩阵的基础上增加第3、6、9 行和列，并将z坐标所对应元素置0，可得：

其中：

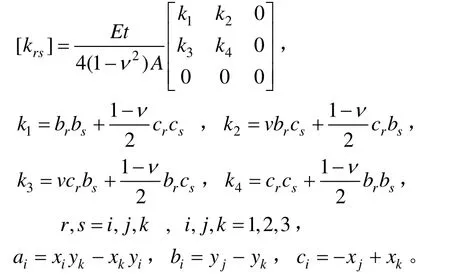
2.4 刚体准则检验

设1C状态下单元处于平衡状态，基于UL 格式，建立结构在2C状态的增量虚功方程，则单元的增量平衡方程为[8]：

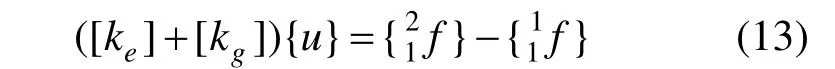
式中：｛u｝ 表示C1状态到C2状态单元结点位移增量； {}为以C1状态为参考的C2状态下的结点力向量；｛｝为以C1状态为参考的C1状态下的结点力向量，为：

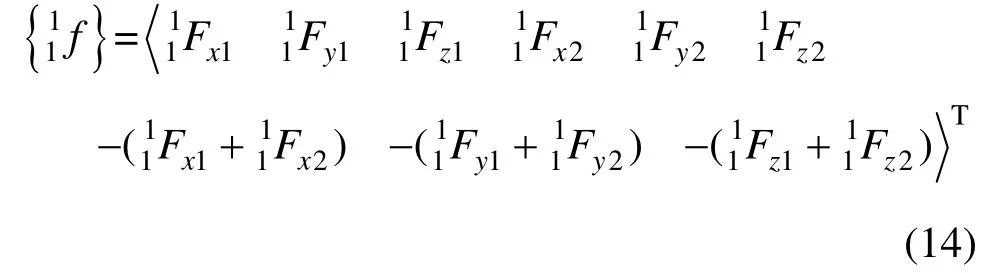
假设膜单元绕z轴逆时针刚性转动 180o到达C2状态，如图6 中实线所示，此过程中单元刚体位移向量{u}r为：

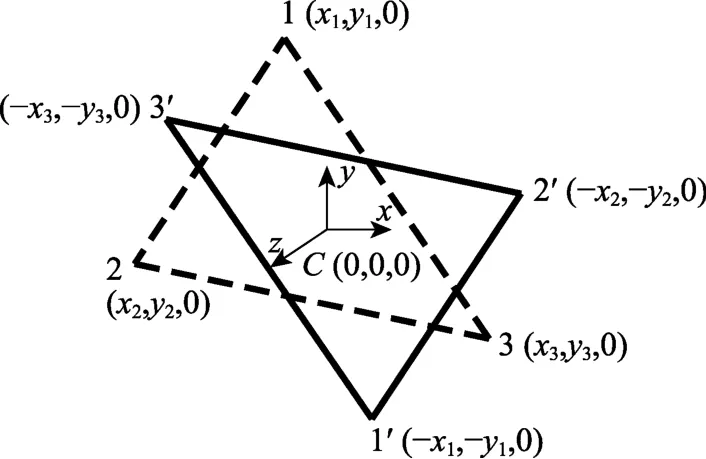
图6 三角形空间膜单元的刚体位移 Fig.6 Rigid body motion of TSME

易证明弹性刚度矩阵[ke]在刚体位移下不会产生单元结点力增量，即：

当单元只发生刚体位移{ }ru时，式(13)左侧变为：

其中：

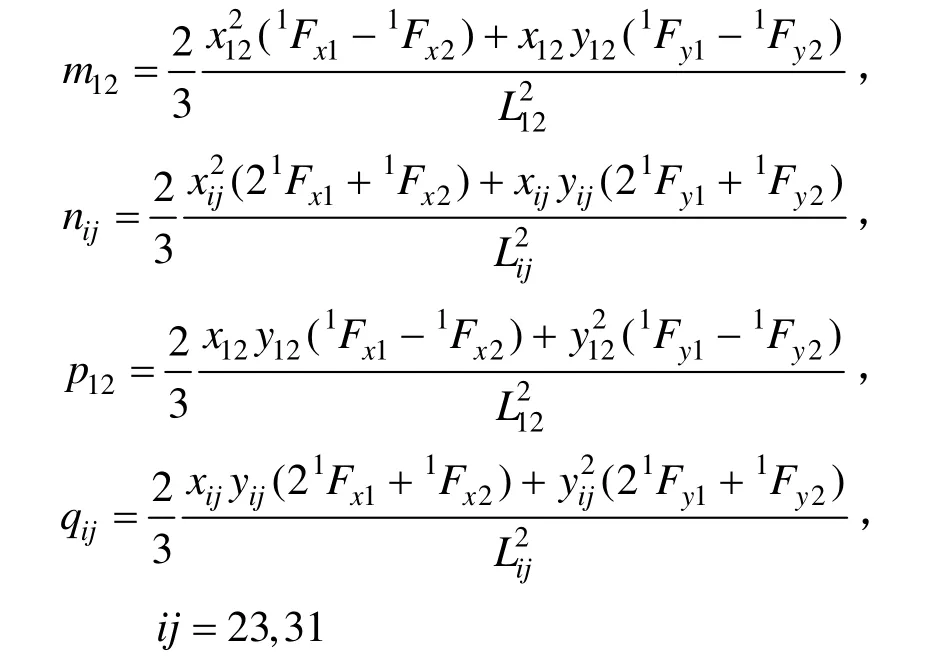
显然，单元在发生刚体位移后，仍然满足平衡条件，即弹性刚度矩阵和几何刚度矩阵在刚体位移上所作虚功为零，由此证明了本文所推导的空间膜单元几何刚度矩阵满足虚功原理。

3 三角形平面膜单元

三角形平面膜单元(Triangular plane membrane element, 简称TPME)可由三角形空间膜单元退化而成，如图7 所示，设三角形平面膜单元每个结点包含两个平面内平动自由度。

与三角形空间膜单元的构成类似，可将三角形平面膜单元看作是在平面杆单元构成的铰接三角形内部张拉薄膜而成，如图8 所示。其单元几何刚度矩阵即为平面杆单元构成的铰接三角形的几何刚度矩阵。单元坐标系下三角形平面膜单元的结点力如图8(a)所示，平面杆单元的杆端力如图8(b)所示。

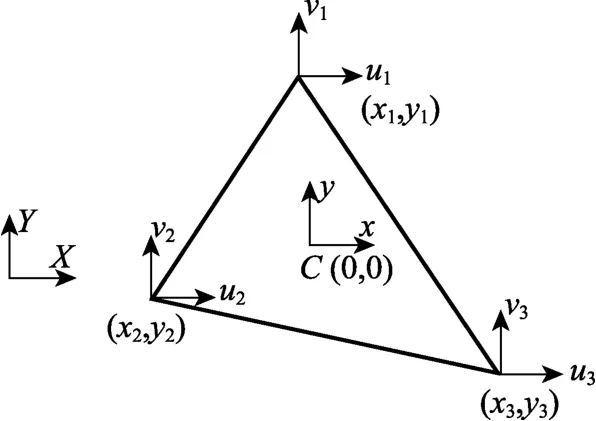
图7 三结点三角形平面膜单元 Fig.7 The TPME with three nodes

C1状态下三角形平面膜单元的结点力向量｛｝可记作：

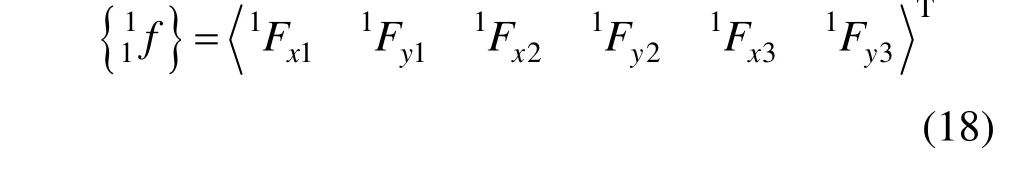
图8 三角形平面膜单元结点力和杆端结点力 Fig.8 The nodal and internal force of TPME

与空间膜单元几何刚度阵推导过程类似，先根据平衡条件，建立平面膜单元坐标系下膜单元结点力与各平面杆单元杆端力之间的关系；而后，将各杆单元的杆端力转换到各杆单元的局部坐标系下，如图9，并将其代入文献[9]中的平面杆单元几何刚度矩阵，得到平面杆单元ij在杆件局部坐标系下的几何刚度矩阵 [kg]2Dbar_ij：

图9 平面杆单元局部坐标系下的杆端力 Fig.9 The internal forces of 2D bar in local coordinate

将杆件局部坐标系下的几何刚度矩阵 [kg]2Dbar_ij转换到膜单元坐标系下，并按单元结点自由度编码对号入座，得到三角形平面膜单元的几何刚度矩阵[kg]TPME：

其中，转换矩阵 2D[ ]T为：

则三角形平面膜单元的几何刚度矩阵 [kg]TPME的具体表达式如下：

其中：

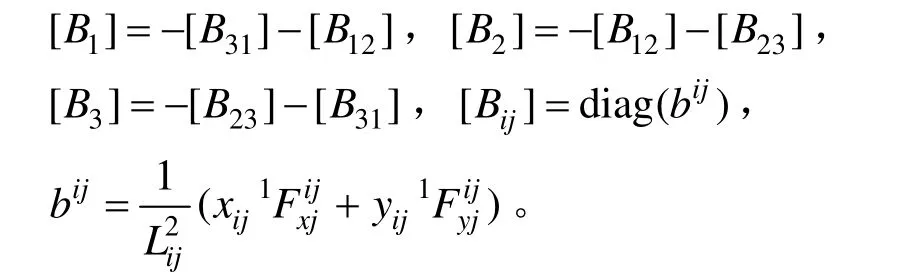
三角形平面膜单元的弹性刚度矩阵即为三角形平面常应力单元的弹性刚度矩阵[13]。

4 UL 列式增量迭代法

非线性分析中，UL 列式的增量迭代法包括三种状态，分别是结构的初始状态0C、上一步平衡状态1C和当前状态2C。非线性分析的增量过程，就是从1C状态到2C状态的结构变形过程。每一增量步中，结构的变形很小，但所有增量步累积可以产生很大的变形。根据前述刚体准则，可将每个增量步所产生的位移增量视为刚体位移和自然变形两部分，其中，刚体位移相对于自然变形大得多。如果在分析的每个阶段都充分考虑刚体位移的作用，则可以采用小变形线性化理论来处理自然变形的剩余影响[14]。

如图10 所示，增量迭代法分为三个阶段：预测阶段、结点力计算阶段和误差判断阶段。预测阶段即计算在给定荷载增量下结构的结点位移增量：

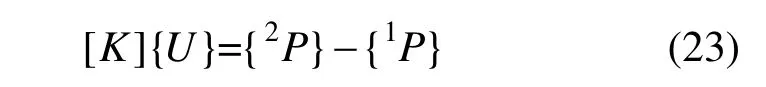
式中， {1P} 和 {2P} 分别表示在C1和C2状态下的外荷载。由结构位移增量{ }UΔ 可以得到各单元的位移增量{ }uΔ ，并叠加得到结构结点位移。显然，预测阶段主要影响迭代次数和收敛速度[14]，在此，结构整体刚度矩阵[ ]K只需近似即可，但需保障迭代方向的正确。对于非线性不显著的问题，可以只采用弹性刚度矩阵，对于非线性显著的结构，结构整体刚度矩阵还需包含结构几何刚度矩阵。

图10 增量-迭代法示意图 Fig.10 Key steps of incremental-iterative analysis method

单元结点力计算阶段是以C2状态为参考，计算在C2状态时的单元结点力。结点力计算决定了整个几何非线性分析的精度。根据刚体准则，由于C1状态平衡的单元结点力，经过刚体运动到C2状态时，仅发生方向的改变而大小不变，因此可以将C1状态的结点力 {}通过坐标变化转动到C2状态。而后基于小变形线性化理论，采用弹性刚度矩阵计算单元结点力增量：

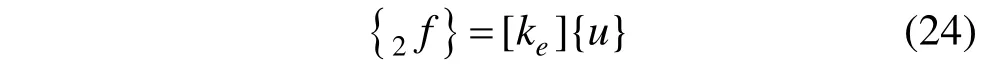
将两部分相加得到以2C为参考状态的2C状态下的单元结点力：

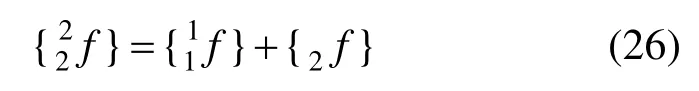
误差判断阶段需计算结点不平衡力。由方程(26)得到2C状态下结构各单元结点力，求和后与总载荷 {2P} 比较，得到C2状态下结构的结点不平衡力。若不平衡力大于收敛值，则进入下一增量步；否则，迭代以消除不平衡力。

以上过程的具体步骤为：

对于第i增量步、第j迭代步的结构增量平衡方程写作[15]：

将式(27)进一步分解为：

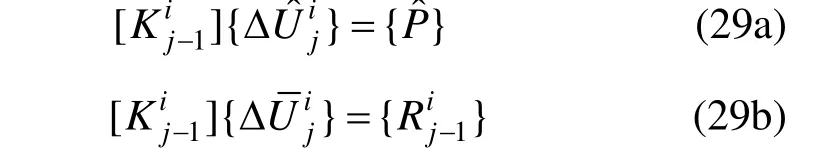
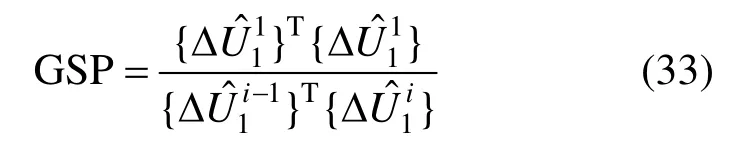
对于第j次( 2j≥ )迭代计算，荷载增量参数i

jλ为：

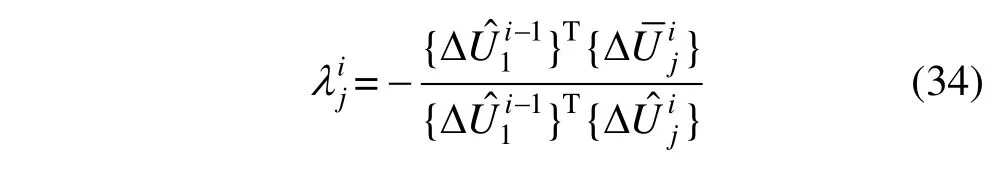
5 算例与分析

以下通过若干算例验证本文所建空间及平面膜单元在几何非线性分析中的适用性、精度及效率。首先，通过悬臂梁端部受集中荷载作用的算例验证本文所建平面膜单元的有效性，再通过内压作用下双抛物线膜结构、双抛物面膜结构等的大变形分析，并与Noguchi 等[3]的无网格伽辽金法(EFG)、Tsiatas 等[4]的有限元法(FEM)和模拟方程法(AEM)、王震等[5,25]的向量式有限元法(VFIFEM)以及商业软件ANSYS 等对比，说明本文所建模型的精度及效率。

算例1. 平面膜单元算例—悬臂梁端部受集中荷载

该算例取自文献[24]，为验证几何非线性分析单元及方法的经典算例。如图11，悬臂梁自由端受集中荷载，考虑平面内弯曲，弹性模量E=10 MPa，泊松比ν=0.3，悬臂梁长∶高∶厚=1000 mm∶100 mm∶10 mm。采用本文所建三角形平面膜单元分析，共划分20 个单元，如图12 所示。此外，还采用ANSYS 中的SHELL63 单元进行对比，单元划分形式同图12，SHELL63 单元每个结点6 个自由度。仅考虑膜的面内刚度，所得悬臂梁端部荷载与竖向位移关系曲线如图13 所示。从中可以看出，本文推导的三角形平面膜单元与 ANSYS 中的SHELL63 单元计算结果高度吻合，但本文所建单元 每个结点仅含两个自由度，且几何刚度矩阵为线性举证，构造简单。

图11 受剪悬臂梁 Fig.11 Cantilever beam subjected to transverse end load

图12 三角形平面膜单元划分方案 Fig.12 Triangular plane membrane element

图13 悬臂梁端部荷载位移曲线 Fig.13 Load-deflection curves for cantilever beam

算例2. 空间膜单元算例—内压下的双抛物线膜片

如图14 所示双抛物线薄膜结构，膜片的投影平面为矩形，其初始形状由以下双抛物线曲面函数所确定[4.26]：

设膜片边长a=b=1000 mm，厚度h=1 mm，中心矢高h=100 mm，弹性模量E=6000 MPa，泊松比ν=0.267，四边简支，膜片内表面受均布内压作用。采用本文所建三角形空间膜单元，共划分200 个单元，如图14 所示，采用前述增量迭代法计算，可以观察到，随着荷载增大，膜片向外膨胀。图15为内压为1.5 MPa 时的变形状态。双曲抛物线膜片形心处荷载-竖向位移曲线绘于图16 中，图中还给出了有限元法(FEM)、Noguchi 等[3]的无网格伽辽金法(EFG)、Tsiatas 等[4]的模拟方程法(AEM)以及王震[5]的向量式有限元法(VFIFEM)的结果予以比较。各方法在不同荷载下的计算结果及与AEM 方法的相对误差见表1。与精度较高的模拟方程法(AEM)[4]的比较可知，无网格伽辽金法(EFG)[3]由于采用忽略膜曲率的应变模型和平面弹性应力-应变关系而计算精度最低，向量式有限元法(VFIFEM)[5]通过划分了800 个三角形常应变薄膜单元而获得了较高的计算精度。本文方法与Tsiatas 等[4]采用200 个三角形壳单元的有限元法所得结果具有相近的精度，但本文所建单元自由度少，几何刚度矩阵构造简单，具有更高的计算效率。

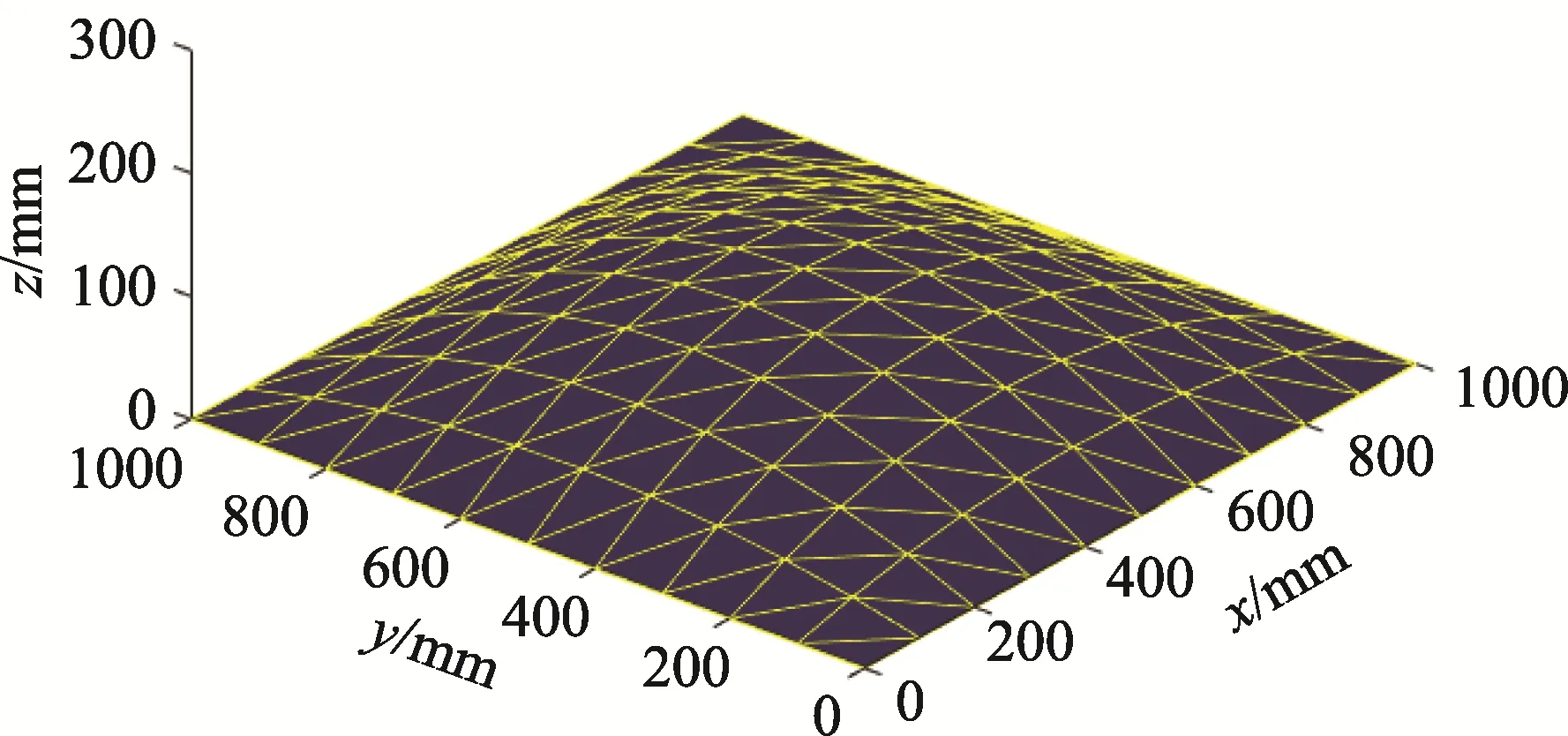
图14 膜片初始未变形状态 Fig.14 Initial undeformed state of the membrane

图15 内压为1.5 MPa 时膜片变形状态 Fig.15 Deformation state under 1.5 MPa of the membrane

图16 双曲抛物线膜片形心处荷载-竖向位移曲线 Fig.16 Central load-deflection curve of the double parabolic membrane

表1 不同计算方法在不同荷载下的 双曲抛物线膜形心竖向位移 Table 1 Central deflection of the double parabolic membrane by different method

算例3. 空间膜单元算例—内压下的双曲抛物面膜片

如图17 所示双曲抛物面薄膜结构，膜片的投影平面形状为矩形，其初始形状由以下双曲抛物面函数所确定[4,27]：

其 中，相 对 矢 高 Δf=C3-C2-C4，C3= 0，C2=C4= 300 mm 。矩形膜片边长a=b=1000 mm，厚度h=3 mm，弹性模量E=6000 MPa，泊松比ν=3，四边简支，膜片内表面受均布内压作用。采用三角形空间膜单元，共划分200 个单元。图18 为内压达到3 MPa 时膜片的变形状态。双曲抛物面膜片形心处荷载-位移曲线绘于图19 中，图中还给出了采用模拟方程法(AEM 法)[4]、有限元法(FEM)[4]以及 向量式有限元法(VFIFEM)[5]的计算结果。不同方法在不同荷载下的计算结果与相对误差见表2。与精度较高的AEM 的比较可知，VFIFEM 法[5]划分了800 个单元而获得了较高的计算精度，FEM 法[4]采用了高次插值的三角形膜单元，同样划分200 个单元，但计算精度略低于本文方法。表明本文所建空间膜单元对膜结构几何非线性分析具有较高的精度和效率。

图17 初始未变形状态 Fig.17 Initial undeformed state of the membrane

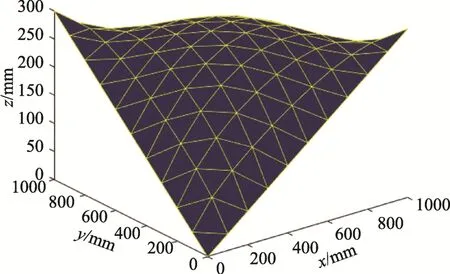
图18 内压为3.0 MPa 时变形状态 Fig.18 Deformation state under 3.0 MPa of the membrane

图19 双曲抛物面膜片中心荷载-位移曲线 Fig.19 Central load-deflection curve of the hyperbolic paraboloidal membrane

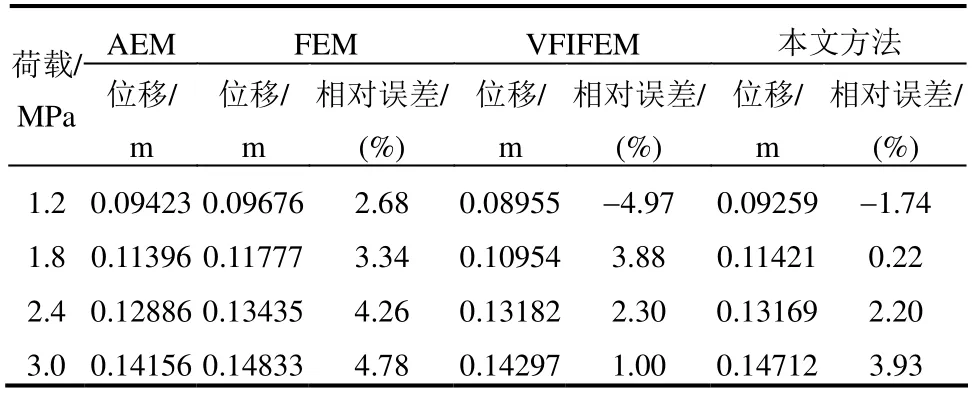
表2 不同计算方法在不同荷载下的双曲抛物 面膜形心竖向位移 Table 2 Central deflection of the hyperbolic paraboloidal membrane by different method

6 结论

本文应用刚体准则，基于UL 列式，建立了一种新的弹性非线性分析膜单元及其相应非线性分析增量迭代法。本文所构造的三角形膜单元，由三根空间杆件组成铰接三角形，并在中间张拉薄膜而成，杆件的材料与薄膜相同，这符合三角形的稳定性，即三角形的形状及位置由其三条边的位置和长度可唯一确定。该膜单元的整体位形由杆单元构成的空间铰接三角形确定，其几何刚度矩阵由杆件铰接三角形的几何刚度矩阵推导得到；而膜单元的弹性变形则由内部张拉的薄膜变形确定，其弹性刚度矩阵即为常规膜单元的弹性刚度矩阵。由此建立的空间膜单元和平面膜单元均通过了刚体准则检验。即初始平衡的单元，结点力在刚体位移上的虚功为零。

在此单元基础上，本文所建立的非线性分析方法，以UL 列式的增量迭代法为依托，在非线性分析的增量迭代法的每个阶段充分考虑了刚体转动的影响，然后利用小变形线性化理论处理剩余的自然变形的影响。在UL 型增量迭代法的预测阶段，所用的刚度矩阵[ ]K为弹性刚度矩阵和几何刚度矩阵的组合，该阶段几何刚度矩阵[kg]不必很准确，可以采用现有软件通行的刚度矩阵，只要保障增量方向正确即可；在单元结点力计算阶段，则需合理计算由单元大转动大位移引起的结点力增量，为此，首先利用刚体准则更新1C状态的单元结点力，而后基于小变形线性化理论，仅用弹性刚度矩阵计算结点力增量。

上述基于刚体准则的思想构造的三角形空间膜单元，其几何刚度矩阵推导过程物理意义明确清晰，且由空间膜单元容易地退化得到平面膜单元。所作经典算例分析以及与已有分析方法、商业软件的对比表明，所建三角形空间膜单元能有效的模拟空间膜结构的大变形和大转动行为，且显示了较高的计算精度和计算效率。