有限元法中间构形初始解预示的 Laplace-Beltrami 方程法
2020-06-01刘永财陈文亮胡庆婉鲍益东
刘永财,陈文亮,胡庆婉,鲍益东
(1. 南京航空航天大学机电学院,江苏省精密与微细制造技术重点实验室,南京 210016; 2. 曲靖师范学院数学与统计学院,曲靖 655011)
在板料成形有限元模拟领域,基于全量理论的一步成形有限元法[1]仅考虑初始构形和最终构形,计算效率高,能够快速计算板料的初始厚度以及应变等物理量分布,得到了广泛的应用。但是,一步成形有限元法也带来最终零件的应力精度估计不足的问题。为弥补这一不足,人们通过引入中间构形的方式来表征加载路径和变形历史,提出了多步成形有限元法[2-3],也称为伪逆法(pseudo inverse approach)[4-5],该方法被广泛应用于板料冲压成形领域[6]。在多步成形有限元法中,如何快速准确的求解出中间构形是其中的一个关键问题。基于虚位移原理[7],采用弹塑性有限元模型,中间构形可以看作是一个关于节点位移的非线性平衡问题,这类问题通常采用Newton-Raphson 迭代法求解。由于迭代法的收敛性强烈依赖于初值与真实值的逼近程度,因此,一个快速准确的中间构形初始解预示算法,对于有限元多步法的收敛效率,具有重要的作用。
中间构形初始解的预示算法得到了众多学者广泛的研究。Lee 等[8]首先提出了采用映射函数的反向映射法,该方法可以处理倾角较大的零件,然而对于复杂的成形零件却难以找到对应的映射函数。Kim 等[9]提出了网格映射法,这种方法需要将零件进行分区处理,算法实现复杂,而且分区对最终结果影响较大,稳定性较差。在截面线法的基础上,吴建军等[10]提出了双展开平面映射法,该方法使用截面线法对两个空间形状进行平面展开,简化了计算量,但是对于局部网格畸变程度大等情况,计算结果仍不理想。Guo 等[11]基于最小面积法的思想,使用序列二次规划(SQP)算法求解一系列约束条件下的最小弧长问题。Tang 等[12]将最小面积法扩展到方盒件等形状规则零件上的初始解预示应用上。然而,最小面积法程序实现繁琐,通用性较差,对于复杂的成形零件难以得到理想的结果。张向奎等[13-14]以三角形单元面积平方和最小为目标函数,提出了伪最小面积法,基于板料变形过程中单元节点不发生横向位移的假设,将问题转化为求解一系列的非线性最小二乘问题,但是该方法没有考虑横向位移外其他方向上的位移。Fu 等[15]通过网格单元位置信息,基于网格参数平面化的思想实现了柱坐标下的初始解预示,并将其用于管材的有限元成形模拟中。陈伟等[16]研究了多步正成形算法中的中间构形初始解预示算法,根据初始平板料和工具曲面展平板料之间的映射对应关系,在两个空间形状间进行插值计算,结合接触判断和修正算法,得到中间构形的初始形状,然而初始形状强烈依赖于工具曲面的展平板料形状。鲍益东等[17]使用张拉膜单元方法计算中间构形初始解,并将其成功集成到自主开发的板料快速模拟成形QuickForm 软件中。然而,该方法需要求解一系列复杂的非线性方程组,计算效率较低。
本文将利用解耦格式对中间构形进行分解计算,推导节点位移约束条件,首次利用构造线性Laplace-Beltrami(LB)方程模型来计算中间构形的初始解,该方法仅需少量的线性迭代就可以快速地生成非对称复杂零件的性态良好初始解。数值算例表明,采用LB 方程的方法能快速准确地生成中间构形的初始解,加快迭代法的收敛速度,减少多步有限元法的运行时间。
1 解耦格式
在多步有限元法中,将中间构形分解为弯曲变形和拉伸变形的解耦格式,采用该格式求解能够增加步长以及加快收敛速度。
根据虚位移原理,在任一时刻,有:
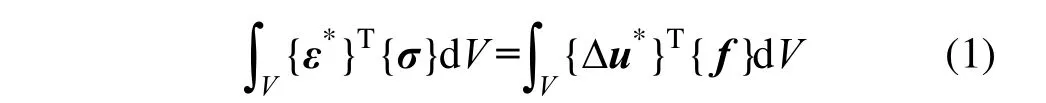
式中:ε*是虚应变;σ是应力; Δu*是虚位移增量;f是外力;V是体积。注意到虚位移的任意性以及应变与位移的几何关系和应力与应变的本构关系,则在t时刻下,可以得到的有限元系统的平衡条件为:

式中:tF表示t时刻外部作用节点力;tR表示t时刻单元应力的节点力。
在t+Δt时刻下,有平衡条件:t+ΔtF-t+ΔtR=0,假设tR已知,令R=t+ΔtR-tR,并将该向量近似为R=tK·ΔU,则有:
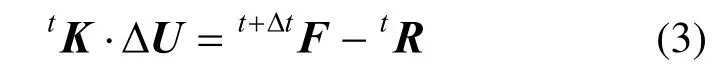
将刚度矩阵Kt看成由膜单元刚度矩阵和弯曲刚度矩阵两部分组成的,因此,如图1 所示,在节点所在的局部坐标系中,可以建立如下方程组来求解时刻tt+Δ 的中间构形[18]:

式中:1Δu和 2Δu为待求解节点的位移增量向量;0u为指定节点的位移向量;t t+ΔF为tt+Δ 时刻外力在切平面上引起的外部作用的摩擦力向量;tR1和tR2分别为t时刻指定节点的位移在法线方向上和切平面上所产生的力向量;tKmij和tKgij(i,j=1,2)分别为t时刻下的膜单元刚度矩阵和弯曲单元刚度矩阵。利用坐标系之间的转换关系,对式(4)进行坐标转换。首先,将方程组从节点所在的局部坐标系转换到单元局部坐标系中,再从单元局部坐标系转换到全局坐标系中,从而得到全局坐标系中的整体有限元方程组。在转换的过程中,节点局部坐标系下的单元刚度矩阵被转换为全局坐标系下的单元刚度矩阵,而膜单元矩阵中的元素值远远大于弯曲单元矩阵中的元素值,这将导致方程组高度病态,造成迭代无法快速收敛甚至迭代发散。
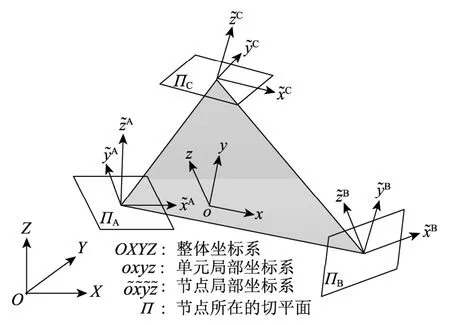
图1 单元坐标系统 Fig.1 Element coordinate systems
为了解决上述问题,本文将薄板的中间构形计算分解为弯曲变形和拉伸变形两个独立的解耦计算过程。它假设节点法向与其邻接的有限元网格法向之间的夹角均可以忽略不计,那么,在法线方向和切平面上,式(4)将被解耦分解为式(5)和式(6):
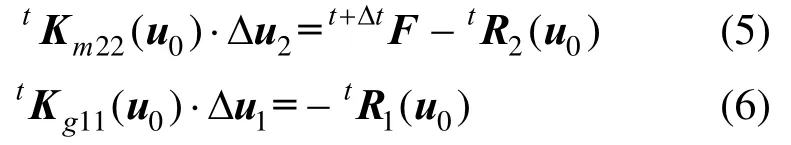
式(5)对应薄板的弯曲变形,式(6)对应薄板的拉伸 变形。
为了精确满足tt+Δ 时刻下有限元系统的平衡条件,需要使用Newton-Rapshon 法[19]对式(5)进行增量迭代求解,即:
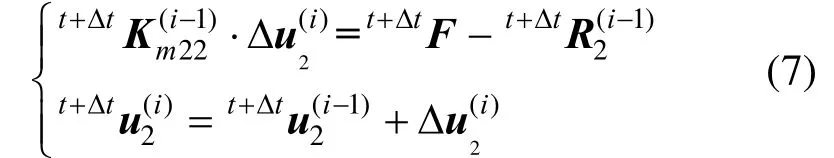
式中,i= 1,2,3,…,初始条件为:
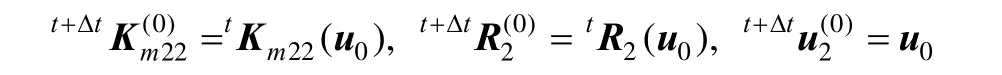
对式(6)的Newton-Rapshon 迭代法求解可以类似 得到。
可以看出,解耦格式在计算上能够带来两方面优势:它将一个大型方程组分解为两个小型方程组;两个小型方程组单元刚度矩阵中的元素值相差不大,条件数得到有效的改善,因此可以加快迭代算法的收敛速度。
综上所述,中间构形被分解为弯曲变形和拉伸变形两个计算过程。其中,以弯曲变形为初始解,通过弹塑性流动力学进行迭代求解来计算拉伸变形,该结果为一个中间构形。本文只研究计算弯曲变形,称其为中间构形初始解。可以看出,一个高效的中间构形初始解构造方法十分必要。由于Laplace-Beltrami 方程具有坚实的数学理论和明确的物理意义,它已经被成功应用到数字几何处理领域,受到了广泛的关注和研究。下面将研究使用LB方程来构造中间构形初始解。
2 Laplace-Beltrami 方程
考虑一个嵌入三维空间的二维曲面,它定义了一个黎曼流形空间。假设g=(gij)2×2该流形空间上的度量张量,则标量函数f的LB 算子[20]可以表示为:
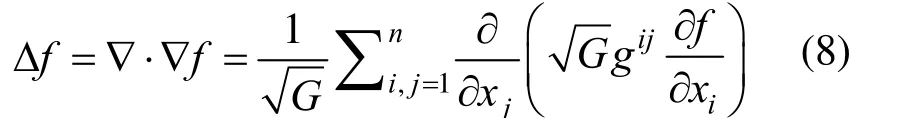
式中,G=det(g),(gij) =(gij)-1,而gij是两个协变张量基做内积的结果。然而,对于一般的复杂曲面,则很难得到连续情形下LB 算子的显式表达式。因此,在实际应用中,通常将待处理的复杂曲面表示为离散的多边形网格形式,并在网格上构造离散LB算子的显式表达式[21]。
这里以三角形网格为例来说明离散LB 算子表达式的构造。首先考虑在某一顶点vi处的一阶离散LB 算 子ci=-x(i+1)mod3+x(i+2)mod3,(i= 1,2,3)的 表达式,写成如下形式:

式中:M表示三角形网格集合;f表示定义在M的函数;MΔ 表示M上LB 算子Δ 的离散逼近;n为M中顶点的个数;ijw为组合系数。从式(9)可以看出,顶点iv处的离散LB 算子可以表示所有顶点函数值的线性组合。
本文选取基于平均曲率计算理论推导的LB 算子的余切表达式[22]为:



图2 Voronoi 区域和角度 Fig.2 Voronoi area and two angles opposite to an edge vivj
可以证明[23],当顶点存在6 个相邻顶点且函数f充分光滑的条件下,如果使用上述式(10)的离散LB 算子ΔM,则它能够以O(h2)的速度收敛于连续LB 算子Δ。其中,h表示三角形网格的尺寸,如图2 所示。

接着,联立所有顶点的一阶离散LB 算子表达式形成一个线性方程组: 式中,W=diag(A1-mixed,A2-mixed, …,An-mixed);b为右端项,LM为对称系数矩阵;当且仅当顶点vi和顶点vj相邻时,(LM)ij具有非零值,即:
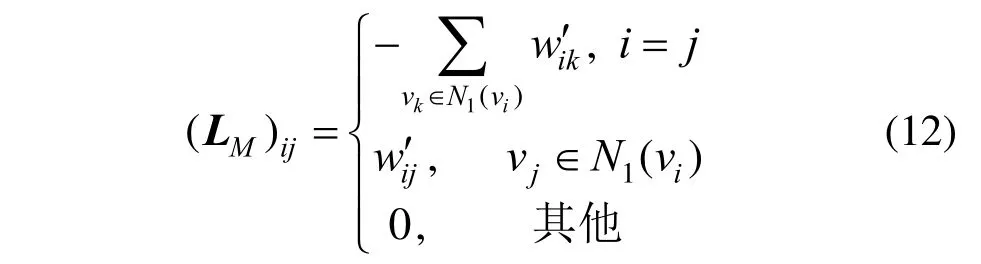
类似地,可以推导出二阶LB 方程为:
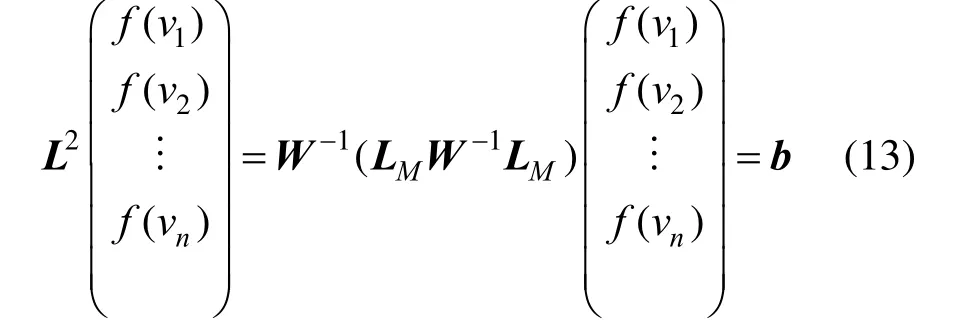
一阶LB 算子对应的是曲面第一基本形式的变化量,而二阶LB 算子对应的是曲面第二基本形式的变化量,为了综合考虑这两种形式的变化量。一般地,将一阶和二阶LB 算子相结合获得LB 方程来表达网格曲面变形,即:
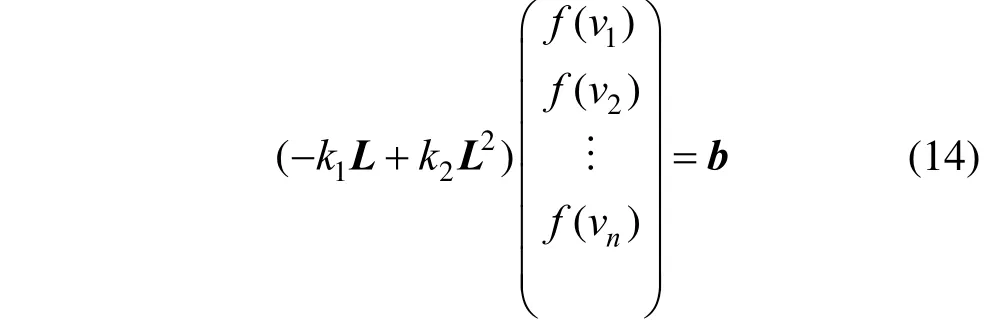
式中,参数1k和2k分别取为1 和10[24]。
LB 方程可以求解约束条件下的网格曲面变形问题。在求解过程中,取f(vi)依次取为节点vi处的空间位置坐标时,则方程组的解为节点更新后的空间位置坐标。此外,为确定出方程的边界条件,需要将网格区域分为固定区域、约束区域和自由区域三部分。其中,固定区域可以通过网格与压边圈或凹模的接触判断来确定,而约束区域和自由区域将通过大位移小应变理论来确定。
3 约束条件及方程求解
在薄板弯曲变形的过程中,尽管结构的位移很大,但是结构的应变却较小,因此它可以视为一个大位移小应变问题[25]。此时,应力和应变之间具有线性关系,满足式(15):

式中:D为弹性矩阵;0σ为初应力,而应变和位移之间具有非线性关系,即:
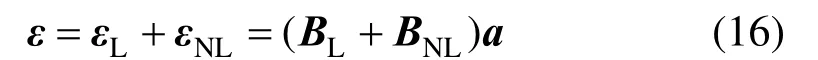
式中:Lε和NLε分别为应变的线性部分和非线性部分;a为节点的位移向量。
下面将给出LB和NLB的计算方法。在全局坐标系下,上一个临时构形Ω和当前临时构形Ω′上的变形前后两个三角形分别记为ABC和A B C′ ′ ′,将它们分别映射到局部坐标系下,并记为abc和a b c′ ′ ′,如图3 所示。在局部坐标系下,三角形单元变形可以视为一个平面问题,可得矩阵LB的表达式:
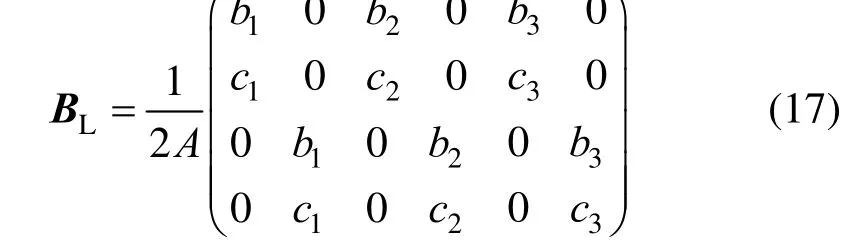
式 中,bi=y(i+1)mod3-y(i+2)mod3和ci=x(i+1)mod3-x(i+2)mod3,(i= 1,2,3)为局部坐标系下三角形abc的三个节点的平面位置坐标。根据变分原理,可推导出矩阵BNL的表达式[26]:

式中,矩阵A中的元素通过式(19)得:

式中,a是三角形三个节点的位移向量。

图3 不同坐标系下的三角形变形描述 Fig.3 Triangle mesh deformation in different coordinate systems
得到LB和NLB后,就可以通过式(16)来计算应变。接着,通过式(15)计算出每个单元的应力,进而得到每个单元所受的内力。根据静力等效原则,通过单元内力能够计算出每个节点处的等效节点力。基于等效节点力,可通过双动情形来建立LB方程的约束条件。
遍历所有与凸模曲面网格发生接触的单元节点,根据等效节点力的方向和法线方向之间夹角大小来判断节点是否为约束节点。
1) 如果两者之间的夹角小于90°,力将节点拉离接触面,当前构形的约束节点在下一个临时构形中成为自由节点,则需要解除该节点的固定约束条件,如图4 中的A点所示;
2) 如果两者之间的夹角大于90°,力将节点继续固定在接触面上,则该节点在下一个临时构形中仍为约束节点,如图4 中的B点所示。
可以看出,随着迭代次数的增加,自由节点的个数逐渐增加,约束节点的个数逐渐减少,直至临时构形满足相应的平衡条件。

图4 约束节点和自由节点示意图 Fig.4 Constraint and free nodes diagram
从式(13)可以看出,矩阵W-1(LMW-1LM)不是对称矩阵。为解决这个问题,在方程的两侧分别左乘W,可得式(20):
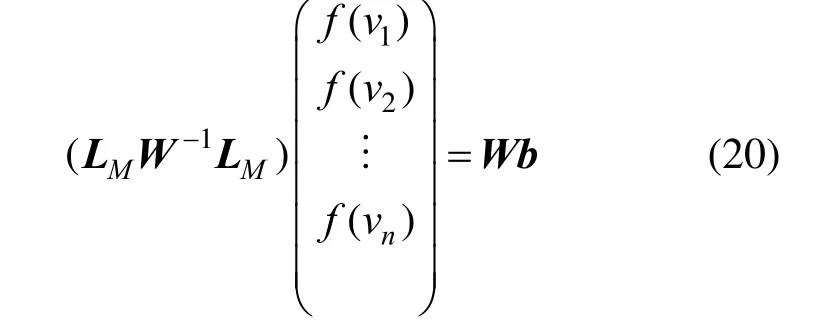
由于LM为对称矩阵,可知式(19)中的系数矩阵LMW-1LM为对称正定矩阵。另外,从LM的稀疏性可知,矩阵LMW-1LM为稀疏矩阵,因此系数矩阵是一个稀疏对称正定矩阵。可采用LU 分解法、多重网格法或共轭梯度法等方法[27]对线性方程组进行数值求解。而当前时间步的中间构形初始解是以上一个时间步中间构形为基础,通过一系列线性方程组迭代求解得到的。在整个迭代过程中,由于上一个时间步的中间构形没有发生改变,因而迭代涉及的系数矩阵保持不变。因此,当使用LU 分解法时,系数矩阵可被分解为上三角矩阵和下三角矩阵的乘积,所以,在迭代过程中仅需要使用追赶法就能准确求解。而对于共轭梯度法,当方程组右端项发生改变的时候,它没有利用系数矩阵不变的特性,需要重新迭代,增加了计算时间。多重网格法虽然计算时间较短,但是程序实现较为困难。因此,结合算法的实现难易和效率好坏综合考虑,本文采用LU 分解法来求解LB 方程。
4 算例
基于解耦算法的多步有限元算法,已经被成功集成到自主开发的板料成形模拟软件QuickForm中。其中,使用LB 方程来构造中间构形初始解。为验证算法的有效性,这里以板料成形商业有限元软件DynaForm 的模拟结果作为标准值,该软件因使用动力显式算法,因为其模拟精度高、可靠性好,已经被广泛应用到覆盖件的板料成形的仿真分析中。
以NUMISHEET’1994 中某汽车翼子板标准零件的冲压成形为例,来说明使用LB 方程中间初始解算法的有效性。该零件凹模的CAD 模型如图5所示。初始坯料的尺寸为1920 mm×1530 mm,厚度为1.0 mm,材料应力-应变关系为σ= 648(ε+ 0.004)0.220MPa,弹性模量为E= 2.07GPa,泊松比为ν= 0.28,冲头力的大小为Fpunch= 280 kN ,摩擦力系数为 0.12μ= 。坯料被划分为11,737 个节点,23,040 个三角形单元网格,拉延深度为130.40 mm。使用测试的计算机处理器为 Inter(R)Core(TM) i5-7300,内存为2.60 GHz。

图5 零件凹模的CAD 模型 Fig.5 CAD model of a die part
图6(a)为拉延深度为90 mm 时,采用LB 方程迭代6 次计算得到的初始中间构形的离散三角形网格。此时,板料被划分为43031 个节点、79923 个单元,相较于原始平板料的网格数有所增加,这是为了更好地表达曲率变化较大处零件特征而对三角形网格进行加密处理的缘故,它的总面积为2945308 mm2。可以看出,算法构造的临时构形网格质量良好,没有出现网格重叠等缺陷。图6(b)给出了迭代1 次,迭代2 次以及迭代3 次的临时中间形状沿截面线截取的部分曲线形状结果对比。从图 6 可以看出,随着迭代次数的增加,曲线上的约束节点个数越来越少,而自由变形的区域越来越大,曲线曲面的光滑性越来越好。
另外,图6 中还分别给出了使用张拉膜单元方法和LB 算子方法沿着截面线得到的中间构形初始解形状。可以看出,两种方法均可以获得良好的中间构形初始解形状,它们得到的结果非常接近。但是,采用相同的迭代终止条件时,两种方法在计算当前步的中间构形初始解所需时间却是不同的,使用张拉膜单元方法计算时间为24.32 s,而使用LB算子方法计算时间为16.68 s。显然,LB 算子方法的计算速度更快,计算效率更高,这是因为它求解的线性方程组维数更少的缘故。

图6 初始中间构形和沿截面线的曲线形状 Fig.6 Intermediate configurations
图7 分别给出了使用DynaForm、QuickForm 和AutoForm 三种软件得到的合模状态下的零件厚度分布图,其中板料成形商业有限元软件AutoForm占有率高,它使用静力隐式算法,具有模拟速度快,计算准确度高的特点。从图7(a)~图7(c)对比中可以看出,三者的厚度分布具有一致的趋势。其中,最大减薄部分均位于零件的相同区域,见图中标记部分,它们分别为0.70 mm、0.79 mm 和0.82 mm,验证了多步法算法的有效性。

图7 DynaForm、QuickForm 和AutoForm 三种软件模拟的板料厚度分布图 Fig.7 Thickness distributions by DynaForm, QuickForm and AutoForm
进一步来分析动力显式算法和静力隐式算法的模拟结果和运行时间。合模状态下零件在XOY平面上的边界轮廓线如图8 所示,三者得到的边界线形状基本一致。其中QuickForm 和DynaForm 两者之间的最大距离为58.5 mm,和零件的总尺寸相比,这里产生的相对误差小于3.12%。三者计算的单元总面积分别为2998960 mm2、3000394 mm2和2954358 mm2,可见静力隐式算法和动力显式算法结果之间的相对误差小于1.5%。然而,在相同的计算机配置下,使用基于动力显式算法的DynaForm软件运行的时间为6899 s,而使用基于静力隐式算法 AutoForm 软件和 QuickForm 软件分别需要1203 s 和1086 s,可见隐式多步成形有限元法的效率大幅提升,大约仅为显式有限元法的16%。进一步,分析基于静力隐式算法的 QuickForm 和AutoForm 的模拟结果和运行时间。如图8 所示,合模状态下的两者计算模拟的边界轮廓线较为接近,而QuickForm 软件较AutoForm 软件的运行时间减少了10.77%,说明本文提出的构造中间解预示算法是快速且有效的。
以汽车某复杂零件的冲压成形为例,来进一步说明本文方法有效性。该零件凸模的CAD 零件图如图 9 所示。初始坯料的尺寸为 1680 mm× 1270 mm,厚度为1.0 mm,材料具体参数为:应力应变关系为σ= 784(ε+ 0.009)0.21MPa,弹性模量为 2.07E= GPa,泊松比为 0.28ν= ,摩擦力系数为。坯料被划分为15 328 个节点,29 436 个三角形单元网格,拉延深度为85 mm。

图8 最终构形的外轮廓图 Fig.8 Contours of final part

图9 零件凸模的CAD 模型 Fig.9 CAD model of a punch part
合模状态下零件在XOY平面上的边界轮廓线如图10 所示,三者得到的边界线形状基本一致。而使用基于动力显式算法的DynaForm 软件运行的时间为4 126 s,而使用基于静力隐式算法AutoForm和QuickForm 软件分别需要782 s 和663 s,可见隐式多步成形有限元法的效率大幅提升,大约仅为显式有限元法的19%,而QuickForm 较AutoForm 的运行时间减少了 15.38%,这说明了集成到QuickForm 软件中的LB 算子方程方法来预示中间构形是快速且有效的。

图10 某复杂零件最终构形的外轮廓图 Fig.10 Contours of final part for a complicated part
5 结论
在多步成形有限元法中,本文将中间构形的构造分解为拉伸变形和弯曲变形的解耦格式;根据大位移应变的理论,推导了中间构形的节点位移约束,给出了利用LB 方程求解中间构形的初始解预示算法。通过数值实验结果表明:
(1) 在多步有限元法中采用解耦格式,增加了每步的行进步长,有效地改善了方程组的条件数,具有更好地数值求解稳定性和收敛性,提高了有限元法的计算效率。
(2) 基于大位移应变理论推导位移约束,能够有效地模拟出弯曲变形过程中的节点位置变化移动情况。
(3) 通过离散的LB 算子线性方程来进行中间构形的初始解预示,算法实现简单、通用性强、计算速度快。
