负载电阻下变论域模糊PI控制对Buck-Boost变换器的影响
2020-06-01杨铠睿祝熙彤姜锐函徐红梅
杨铠睿, 祝熙彤, 姜锐函, 徐红梅
( 延边大学 工学院, 吉林 延吉 133002 )
0 引言
Buck-Boost变换器因具有升压和降压功能,被广泛应用于照明设备、新能源汽车等领域[1].Buck-Boost变换器属于非最小相位系统,易受外部环境干扰,且内部参数变化也会影响其性能,因此在使用Buck-Boost变换器时需引入控制环节来提高系统的稳定性[2].目前,Buck-Boost变换器多采用线性PI控制方法[3]来提高系统的稳定性,该方法虽然可以提高系统鲁棒性,但因实际电路系统均为非线性系统,因此该PI控制方法难以达到最佳控制效果[4].为改善上述问题,2019年,黄梦涛等[5]将变论域应用在PID控制系统中,结果显示该方法可提高系统的稳态性能.目前为止,未有文献报道变论域是否适用于PI控制系统.为此,本文提出一种变论域模糊PI控制器,并利用Matlab/Simulink仿真对比分析负载电阻参数突变时,传统PI控制器、模糊PI控制器和变论域模糊PI控制器在Buck-Boost变换器系统中的控制精度和响应速度,以此验证变论域模糊PI控制器在Buck-Boost变换器系统中的控制性能.
1 Buck-Boost变换器工作原理

图1 Buck-Boost变换器的电路拓扑结构
Buck-Boost变换器的电路拓扑结构如图1所示.开关S接通时,二极管D截止,电感L储存能量,电容C中的能量为负载R供电,负载两端电压为上负下正;开关S断开时,二极管D导通,电容C储存能量,电感L为负载R供电,负载两端电压为上负下正,与输入电压极性相反.
在稳态导通状态下,Buck-Boost电路系统的线性动态方程[6]为
(1)
将式(1)进行拉氏变换可得
x(s)=(sE-A)-{Bu(s)+[(A1-A2)X+(B1-B2)U]d0(s)}.
(2)

(3)
由式(2)和式(3)可得输出电压VO与占空比D的传递函数为
(4)

图2 未进行PI控制前的Buck-Boost变换器的伯德图
由式(4)可知输出电压与占空比的传递函数存在正实根,即S平面右半平面存在一个零点,因此可判定Buck-Boost变换器系统为非最小相位系统.为验证Buck-Boost变换器系统的稳定性,利用Matlab绘制未进行PI控制前的Buck-Boost变换器的伯德图,如图2所示.由图2可知变换器系统的相位裕量为-39.1 dB,幅值裕量为-75.8 deg,由此表明系统是不稳定的,需引入控制环节.绘制伯德图时相关参数的设置如表1所示.

表1 绘制伯德图时Buck-Boost变换器的相关参数
2 Buck-Boost变换器的PI控制器模型
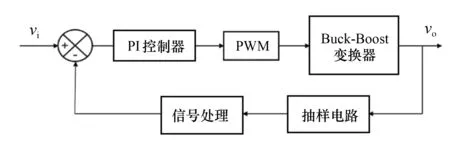
图3 传统PI控制器的流程图
为改善Buck-Boost变换器系统的稳定性,本文采用PI控制器对Buck-Boost变换器的稳定性能进行补偿.实现Buck-Boost变换器的PI控制,只需将输出电压反馈至输入端并对其进行串联校正即可[7].传统PI控制器的流程图如图3所示.
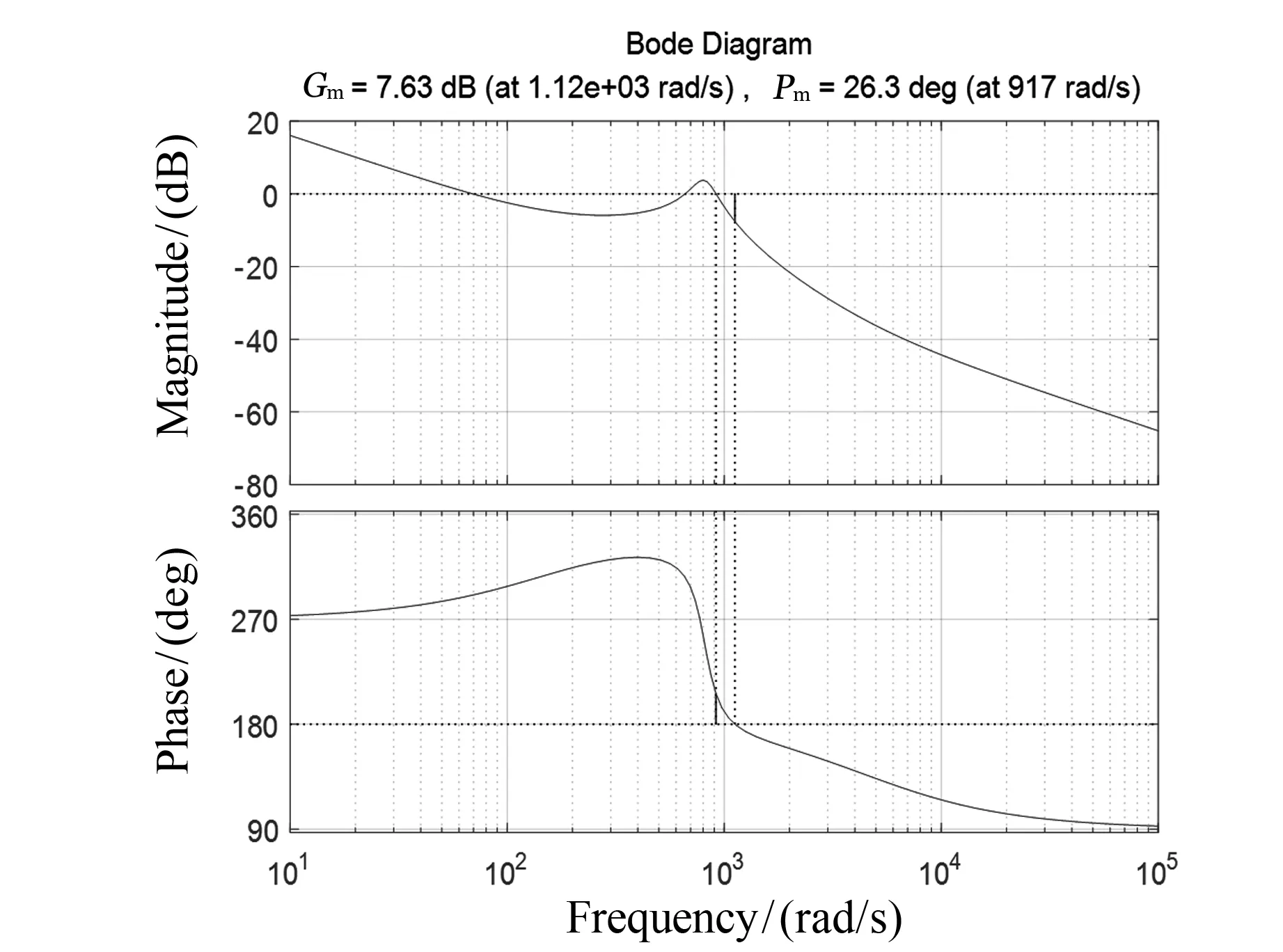
图4 补偿后Buck-Boost变换器的伯德图
采用PI控制器对Buck -Boost变换器的稳定性能进行补偿的具体方法为:建立PI控制器模型;在pidTuner中利用系统的开环传递函数计算PI控制系统的比例系数和积分系数;根据仿真结果调整比例系数和积分系数.经仿真实验本文最终选取的比例系数Kp为0.002 8,积分系数Ki为0.004 6.为检测补偿后的Buck-Boost变换器系统的稳定性,绘制补偿后变换器系统的伯德图,如图4所示.由图4可知,相位裕量为7.63 dB,幅值裕量为26.3 deg,这表明系统的稳定性较强.对传统PI控制器进行补偿后系统虽然趋于稳定,但因传统PI控制器属于线性控制方法,当受到外部干扰时系统仍会变得不稳定[8],因此需对控制器进行进一步改进.
3 Buck-Boost变换器的变论域模糊PI控制器模型
模糊控制是一种动态响应特性良好的非线性控制,能够通过实时调整系统参数来提高系统的动态性能[9],且可不依赖于系统的固定模型[10].因此本文将模糊控制与PI控制结合,以此根据误差来实时调整PI控制器的参数,减少外部干扰.模糊控制与PI控制结合的模糊PI控制器如图5所示,图5中e为输入量误差,ec为误差率.输入与输出变量采用如图6所示高斯隶属度函数进行计算,其中NB、NM、ZE、PM、PB分别表示负大、负小、零、正小、正大.模糊PI控制器根据上述参数的变化及模糊规则即可得出Kp与Ki的调整量ΔKp和ΔKi, 并以此使系统适应参数变化所带来的影响.
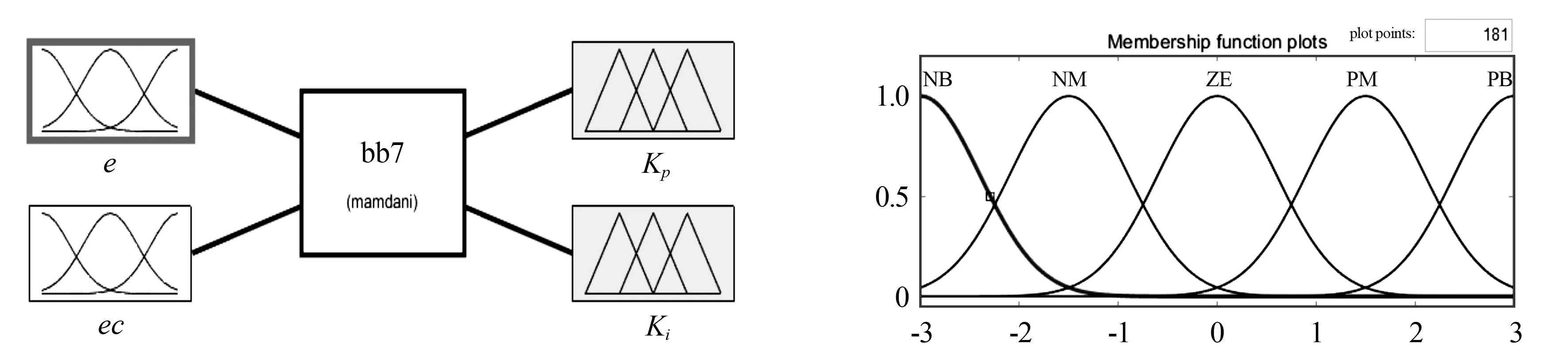
图5 模糊PI控制器示意图 图6 高斯隶属度函数示意图
4 各控制器在负载电阻变化情况下的仿真结果与分析
在Matlab/Simulink中建立Buck -Boost变换器的电路仿真模型,并分别利用传统PI控制器、模糊PI控制器和变论域模糊PI控制器对变换器的电路进行控制.各仿真电路模型如图7—图9所示,电路的相关参数按表1设置.

图7 传统PI控制器的仿真电路

图8 模糊PI控制器的仿真电路

图9 变论域模糊PI控制器的仿真电路
3种控制器在电阻参数突变前的输出电压波形图如图10所示.图10中横坐标为仿真时间,纵坐标为输出电压.由图10可以看出,变论域模糊PI控制器在系统精度、系统稳定状态和调节时间方面均优于传统PI控制器和模糊PI控制器.

图10 3种控制器在负载电阻突变前的输出仿真电压波形
为分析负载电阻参数突变时各控制器的控制效果,在仿真时间达到0.15 s时对负载电阻参数进行减小和增大.当负载电阻参数由10 Ω突然减小到5 Ω时,各控制器的输出电压波形图如图11所示.由图11可以看出,参数发生突变后: (a)传统PI控制器的输出电压波形在调节时间达到0.110 s后趋于稳定的等幅振荡状态,稳态误差为0.86 V; (b)模糊PI控制器的输出电压波形在调节时间达到0.070 s后呈现稳定的等幅振荡状态,稳态误差为0.62 V; (c)变论域模糊PI控制器的输出电压波形在调节时间达到0.046 s后达到稳定的等幅振荡状态,稳态误差为0.27 V.由此可知变论域模糊PI控制在负载电阻参数突然减小时其响应速度和控制精度均优于传统PI控制和模糊PI控制.
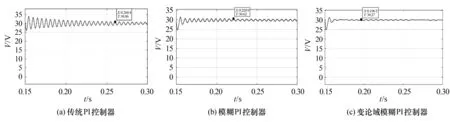
图11 3种控制器在负载电阻由10 Ω突变为5 Ω时的仿真输出电压波形
当负载电阻参数由10 Ω突然增大到15 Ω时,模糊PI控制器和变论域模糊PI控制器的输出电压波形如图12所示.由图12可以看出,模糊PI控制器的输出电压波形在调节时间达到0.053 s后趋于等幅振荡状态,稳态误差为0.33 V;变论域模糊PI控制器的输出电压波形在调节时间达到0.037 s后稳定在等幅振荡状态,稳态误差为0.24 V.由此表明变论域模糊PI控制在负载参数突然增大时其控制精度和响应速度均优于模糊PI控制.

图12 2种控制器在负载电阻由10 Ω突变为15 Ω时的仿真输出电压波形
5 各控制器在输入电压突降时的仿真结果与分析
为验证负载电阻参数不变,输入电压突降时变论域模糊PI控制器的控制性能,在负载电阻参数为10 Ω和仿真时间为0.15 s的条件下,将输入电压从20 V突降为15 V,其仿真结果如图13所示.由图13可知,当输入电压从20 V突降为15 V时,传统PI控制器的输出电压波形在调节时间达到0.083 s后达到等幅振荡状态,稳态误差为3.32 V;模糊PI控制器的输出电压波形在调节时间达到0.069 s后达到稳定状态,稳态误差为0.23 V;变论域模糊PI控制器的输出电压波形在调节时间达到0.056 s后达到稳定状态,稳态误差为0.12 V.由此可知,当负载不变、输入电压突然减小时,变论域模糊PI控制器的控制精度和响应速度均优于传统PI控制器和模糊PI控制器.

图13 3种控制器在输入电压突降时的仿真输出电压波形
6 结论
本文在Buck-Boost变换器负载电阻参数变化的情况下,利用Matlab/Simulink仿真实验分别对PI控制器、模糊PI控制器和变论域模糊PI控制器的性能进行了研究.研究结果表明,变论域模糊PI控制的控制精度和响应速度均显著优于其他2种控制器.另外,在负载电阻参数不变,突降负载电压时,变论域模糊PI控制器的控制精度和响应速度也优于传统PI控制器和模糊PI控制器.本文结果对改善Buck-Boost变换器系统的稳定性具有很好的参考价值.负载电阻参数不变,突增负载电压时变论域模糊PI控制器的控制效果将做后续报道.
