不确定整数阶和分数阶Rössler混沌系统的自适应滑模同步
2020-06-01程春蕊毛北行
程春蕊,毛北行
(郑州航空工业管理学院 数学学院, 河南 郑州 450015)
混沌是一种复杂的非线性现象,在物理和工程中有很多潜在应用,因此混沌系统的同步控制引起了广泛关注[1-2].分数阶微积分跟整数阶微积分几乎有同样长的历史,但应用背景的缺乏及理论的复杂性使其发展缓慢.近年来,越来越多的学者针对分数阶混沌控制和同步开展了研究[3-6].文献[7]研究了分数阶时滞金融系统的滑模同步.文献[8]研究了分数阶Van der pol振子网络的自适应滑模同步.文献[9]研究了分数阶不确定异结构混沌系统的自适应同步.在实践中,由于被控对象的结构变化、测量误差及建模误差等,混沌系统存在模型不确定性和外部扰动问题,导致系统性能下降.因此,模型不确定性和外部扰动的混沌同步问题是一个重要的研究课题.文献[10]研究了具有不确定性和外部扰动的金融混沌系统的同步问题.文献[11]研究了一类整数阶Rössler混沌系统的追踪控制与同步.在上述文献的启发下,笔者结合自适应控制及终端滑模控制,研究具有模型不确定性和外部扰动项的整数阶和分数阶Rössler混沌系统的同步问题.首先构造含有积分项的终端滑模面,证明误差系统在滑模面上具有稳定性;然后设计滑模控制器以及自适应律,使误差系统轨迹到达滑模面;最后,通过数值仿真证明所提方法的有效性.
1 整数阶Rössler混沌系统的滑模同步
Rössler混沌系统[11]为
其中:x1,y1,z1为系统状态量.
当a=0.2,b=0.2,c=5.0时,出现混沌吸引子.初值(x1(0),y1(0),z1(0))取(2,2,2)时,系统状态量x1的时域波形图和系统相图如图1,2所示.

图1 x1的时域波形图
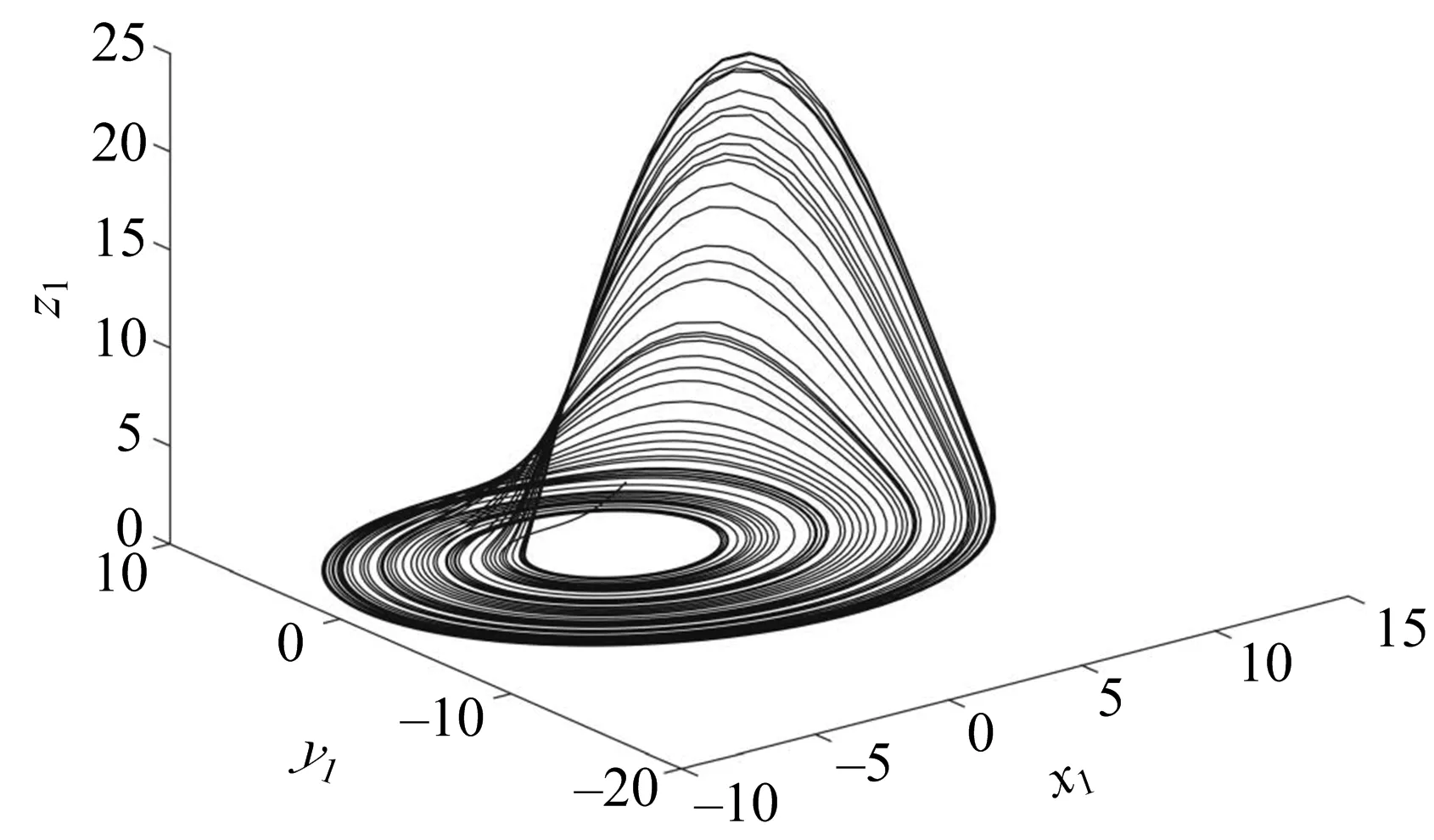
图2 系统相图
设计主系统为
(1)
设计从系统为
(2)
其中:y=[y1,y2,y3]T为系统的状态向量,Δfi(y)(i=1,2,3)为系统的不确定项,di(t)(i=1,2,3)为外部扰动,ui(t)(i=1,2,3)为控制器.
定义误差ei=yi-xi(i=1,2,3), 则有
(3)
假设1不确定项Δfi(y)(i=1,2,3)和外部扰动di(t)(i=1,2,3)均有界,则存在常数mi,ni>0(i=1,2,3),满足
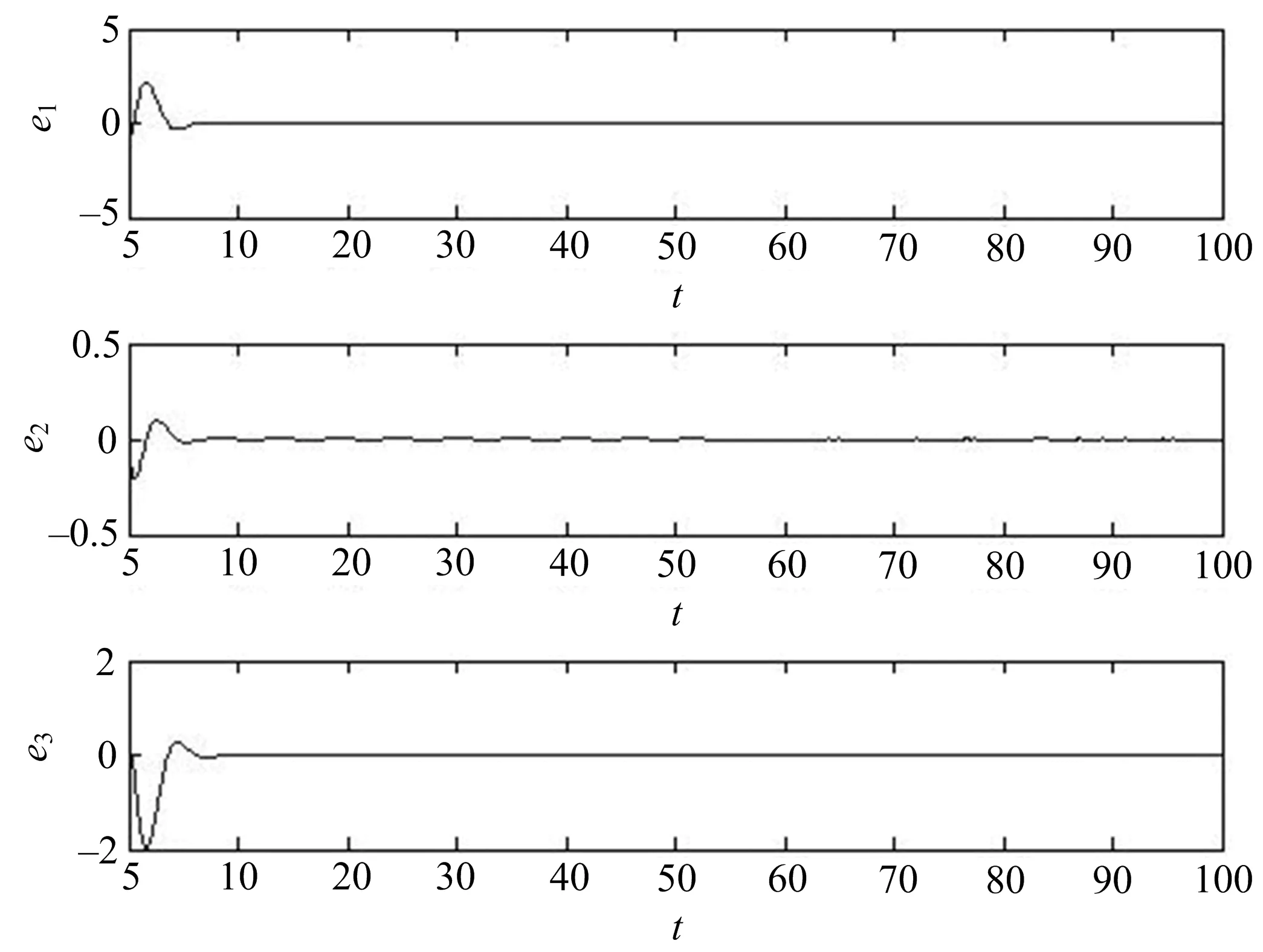
|Δfi(y)| 假设2mi,ni(i=1,2,3)未知. 定理1若系统(3)满足假设1,2, 则构造非奇异终端滑模面为 设计控制器为 并取自适应律为 系统不在滑模面上运动时,构造V(t)为 求导可得 [e1+ae2+λ2e2+Δf2(y)+d2(t)+u2(t)]+s3(t)[y3y1-x3x1-ce3+λ3e3+Δf3(y)+d3(t)+u3(t)]= 定义1[13]定义函数u(t)阶数为α的Caputo分数阶积分为 定义2[13]定义函数x(t)的α阶Caputo分数阶导数为 设计分数阶主系统为 (4) 其中:q∈(0,1). 设计从系统为 (5) 其中:y=[y1,y2,y3]T为系统的状态向量,Δfi(y)为系统的不确定项,di(t)为外部扰动,ui(t)为控制器. 定义误差ei=yi-xi,则有 (6) 引理2[15]若x(t)为连续可微的函数,则对任意的t≥0有 并取自适应律为 从而 故滑模面是稳定的. λ1e1+Δf1(y)+d1(t)+u1(t)]+s2(t)·[e1+ae2+λ2e2+Δf2(y)+d2(t)+u2(t)]+ s3(t)[y3y1-x3x1-ce3+λ3e3+Δf3(y)+d3(t)+u3(t)]. (7) 将控制器及自适应律代入(7)式,且由假设1,2可得 下面通过实例证明所提方法的有效性. 例1整数阶Rössler混沌系统的滑模同步. 在定理1中,设置系统参数为a=0.2,b=0.2,c=5.0, 不确定项为 Δf1(y)=cos(2πy2),Δf2(y)=0.5cos(2πy3),Δf3(y)=0.3cos(2πy2), 外部扰动为d1(t)=0.2cost,d2(t)=0.6sint,d3(t)=cos3t,此时定理1中主系统为 从系统为 对应的误差系统为 (8) 利用Matlab对上述系统进行数值仿真,得到系统(8)的误差曲线如图3所示. 图3 系统(8)的误差曲线 从图3可以看出,状态变量e1,e2,e3在设计的控制器作用下,很快收敛至零点并保持稳定,这表明具有不确定性及外界扰动的整数阶主从Rössler混沌系统能实现同步、所提方法取得了较好的控制效果. 例2分数阶Rössler混沌系统的滑模同步. 在定理2中,设置系统参数为a=0.2,b=0.2,c=5.0,q=0.9, 不确定项为 Δf1(y)=cos(2πy2),Δf2(y)=0.5cos(2πy3),Δf3(y)=0.3cos(2πy2), 外部扰动为d1(t)=0.2cost,d2(t)=0.6sint,d3(t)=cos3t,此时定理2中对应的误差系统为 (9) 利用Matlab对上述系统进行数值仿真,得到系统(9)的误差曲线如图4所示. 图4 系统(9)的误差曲线 从图4可以看出,状态变量e1,e2,e3在设计的控制器作用下,很快收敛至零点并保持稳定,这表明具有不确定性及外界扰动的分数阶主从Rössler混沌系统能实现同步、所提方法取得了较好的控制效果. 针对具有模型不确定性和外部扰动的整数阶和分数阶Rössler混沌系统, 分别提出了适合系统的自适应滑模同步方法.构造了适当的终端滑模面,使系统误差在滑模面上收敛于零.设计了控制律,将误差系统轨迹驱动至滑模面上,保证了滑模运动的发生,实现了整数阶和分数阶主从Rössler混沌系统的同步.数值仿真结果表明所提方法具有较好的同步效果和较强的抗干扰能力.
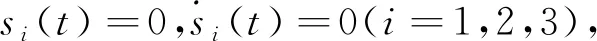
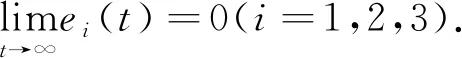
2 分数阶Rössler混沌系统的滑模同步
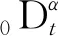

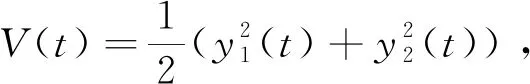
3 数值仿真
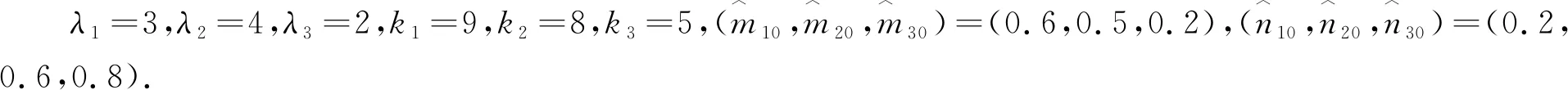
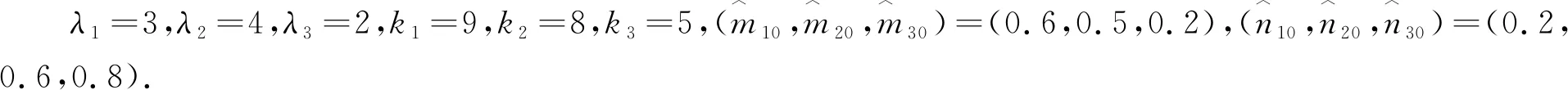

4 结束语
