Morita环上的强Gorenstein投射模

Dadi ASEFA

(上海交通大学 数学科学学院，上海 200240)

Auslander等[1]将有限生成模推广为双边Noether环上Gorenstein维数为零的模．Enochs等[2]将其推广到任意的环上，并称之为Gorenstein投射模．Bennis等[3]又引入了强Gorenstein投射模的概念，证明了一个模是Gorenstein投射模当且仅当它是强Gorenstein投射模的一个直和项，注意到一个Gorenstein投射模并不一定是强Gorenstein投射模．

投射模均是强Gorenstein投射模(反过来一般不正确)，整体维数有限的代数上的Gorenstein投射模均是投射模[4]．Gao等[5]确定了上三角矩阵Artin代数上所有的有限生成强Gorenstein投射模,然而对于具体的非投射的(强)Gorenstein投射模，目前已知的构造并不多见．

Bass[6]在他的著名讲义中引入了Morita环的概念，这类环包含了许多性质较好的代数．受文献[5]的启发，作者希望确定可作为Artin代数的Morita环上所有的有限生成强Gorenstein 投射模，推广了上三角矩阵Artin代数上的强Gorenstein投射模，并且作者的证明与文献[5]中的考虑有所不同．

1 预备知识

设A是有单位元的环．论文用A-Mod表示左A-模范畴，用A-mod表示有限生成左A-模范畴．由文献[4]，称A-模M是A-Mod(A-mod)中的Gorenstein投射模，如果存在A-Mod(A-mod)中投射模的正合列

并且对于任意A-Mod(A-mod)中的投射模Q，HomA(P·,Q)也是正合列， 使得M≅Kerd0．上述P·称为A-Mod(A-mod)中的完全投射分解．称Gorenstein投射A-模M是A-Mod(A-mod)中的强Gorenstein投射模(简称SG-投射模)，如果相应的复形P·形如

用SGProjA(SGProjA)表示A-Mod(A-mod)中由SG-投射模作成的满子范畴．

引理1[5]对任意环A,都成立SGProjA∩A-mod=SGProjA．

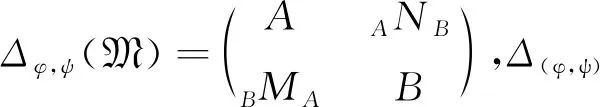
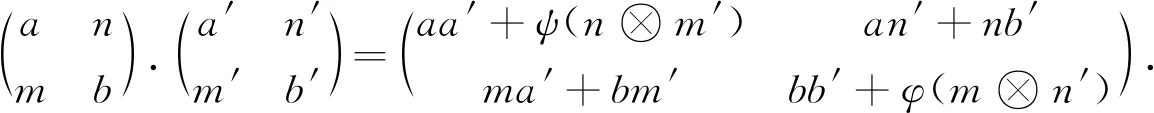
为确保Δ(φ,ψ)作成一个结合环，规定

φ(m⊗n)m′=mψ(n⊗m′),nφ(m⊗n′)=ψ(n⊗m)n′,∀m,m′∈M,∀n,n′∈N．

Morita环Δ(φ,ψ)上模的刻画是已知的结果[6-7]．为了叙述的完整起见，引入下面的范畴,范畴M(Δ)中的对象是4元组(X,Y,f,g)，其中X∈A-mod，Y∈B-mod，f∈HomB(M⊗AX,Y)，g∈HomA(N⊗BY,X)，并且有如下交换图

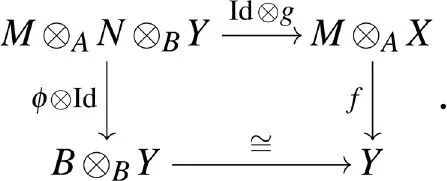
用ψX和φY表示如下态射的合成,有

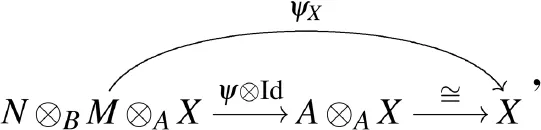
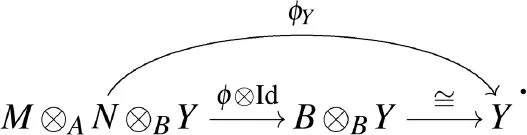
设(X,Y,f,g)和(X′,Y′,f′,g′)为M(Δ)中对象，则M(Δ)中态射(X,Y,f,g)→(X′,Y′,f′,g′)是一对同态(a,b)，其中a:X→X′是A-同态，b:Y→Y′是B-同态，有如下交换图

范畴Δ(φ,ψ)-mod和M(Δ)之间的关系可通过函子F:M(Δ)→Δ(φ,ψ)-mod给出： 对任意的(X,Y,f,g)∈M(Δ)，定义F(X,Y,f,g)=X⊕Y是Abel群，∀a∈A,b∈B,n∈N,m∈M,x∈X,y∈Y,其中的Δ(φ,ψ)-模结构规定为

设(a,b):(X,Y,f,g)→(X′,Y′,f′,g′)是M(Δ)中任意态射，定义

于是函子F是等价函子[7]．今后将Δ(φ,ψ)上的模视为范畴M(Δ)中的对象．

论文主要考虑双模同态为零的且可作为Artin代数的Morita环，记作Δ(0,0)．由文献[8]可知，Morita环Δ(φ,ψ)可作为Artin代数当且仅当存在一个交换Artin环R，使得A和B均为ArtinR-代数，M和N在R上有限生成且中心地作用在M和N上．

(1) 4元组态射序列0→(X1,Y1,f1,g1)→(X2,Y2,f2,g2)→(X3,Y3,f3,g3)→0是Δ(φ,ψ)-mod中的正合列当且仅当0→X1→X2→X3→0是A-mod中的正合列，且 0→Y1→Y2→Y3→0是B-mod中的正合列．

(2) 设(a,b):(X,Y,f,g)→(X′,Y′,f′,g′)是Δ(φ,ψ)-mod中的态射，考虑同态c:Kera→X，d:Kerb→Y，则(a,b)的核为(Kera,Kerb,h,j)，其中态射h和j由如下交换图诱导而得

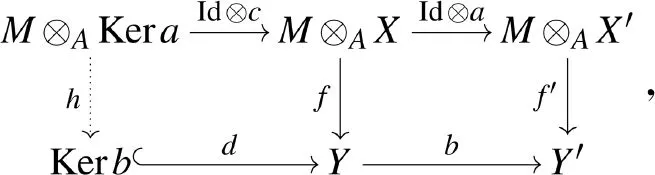
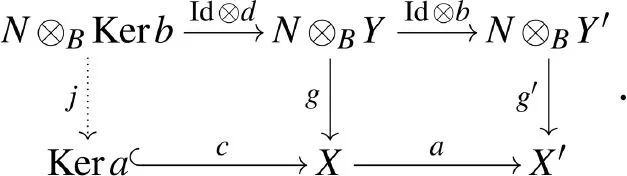
类似地，可以刻画态射(a,b)的余核．类似文献[8]中的处理，考虑下述函子：对任意的X∈A-mod和A-同态a:X→X′，函子TA:A-mod→Δ(φ,ψ)-mod定义为

TA(X):=(X,M⊗AX,IdM⊗AX,ψX),TA(a)=(a,IdM⊗a).

对任意的Y∈B-mod和B-同态b:Y→Y′，函子TB:B-mod→Δ(φ,ψ)-mod定义为

TB(Y):=(N⊗BY,Y,φY,IdN⊗BY),TB(b):=(IdN⊗b,b).

对任意的(X,Y,f,g)∈Δ(φ,ψ)-mod 和Δ(φ,ψ)-态射，有

(a,b):(X,Y,f,g)→(X′,Y′,f′,g′).

函子UA:Δ(φ,ψ)-mod→A-mod 定义为UA(X,Y,f,g):=X,UA(a,b)=:a.

对任意的 (X,Y,f,g)∈Δ(φ,ψ)-mod和Δ(φ,ψ)-态射，有

(a,b):(X,Y,f,g)→(X′,Y′,f′,g′).

函子UB:Δ(φ,ψ)-mod→B-mod定义为UB(X,Y,f,g):=Y,UB(a,b):=b.

对每个Y∈B-mod，记εY:M⊗AHomB(M,Y)→Y为由involution给出的B-同态，构造A-同态δN⊗Y:N⊗BY→HomB(M,M⊗AN⊗BY)，它将n⊗By送到HomB(M,M⊗AN⊗BY)中．对任意的Y∈B-mod和B-同态b:Y→Y′，函子HB:B-mod→Δ(φ,ψ)-mod定义为

HB(Y):=(HomB(M,Y),Y,εY,HomA(M,φY)δN⊗BY),HB(b):=(HomB(M,b),b).

下述结论给出了上述函子的深入刻画．

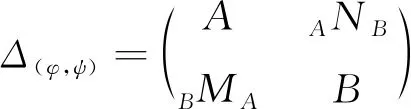
(1) 函子TA，TB，HA和HB都是满且忠实的;

(2) (TA,UA)，(TB,UB)，(UA,HA)和(UB,HB)均为函子的伴随对;

(3) 函子UA和UB均为正合函子．

下述命题给出了不可分解投射(左)Δ(φ,ψ)-模和不可分解内射(左)Δ(φ,ψ)-模的刻画．

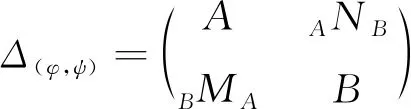
(1) 不可分解投射Δ(φ,ψ)-模恰是

TA(P)=(P,M⊗AP,IdM⊗AP,ψP)，

或

TB(Q)=(N⊗BQ,Q,φQ,IdN⊗BQ),

其中：P跑遍所有不可分解投射A-模，Q跑遍所有不可分解投射B-模．

(2) 不可分解内射Δ(φ,ψ)-模恰是

或

HB(J)=(HomB(M,J),J,εJ,HomB(M,φJ)δN⊗BJ)，

其中:I跑遍所有不可分解内射A-模，J跑遍所有不可分解内射B-模．

2 Morita环上的SG-投射模

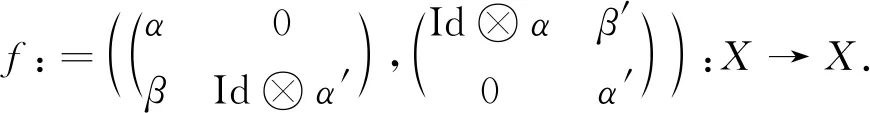
(1)

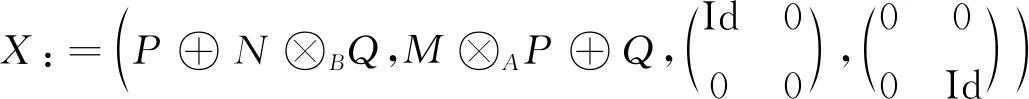
考虑如下条件：

(iii)βα+(Id⊗α′)β=0;

(iv)β′α′+(Id⊗α)β′=0;

(v) 若α(p)=0，β(p)+(Id⊗α′)(x)=0，则存在(p′,x′)∈P⊕N⊗BQ，使得p=α(p′)，x=β(p′)+(Id⊗α′)(x′);

(vi) 若α′(q)=0，β′(q)+(Id⊗α)(y)=0，则存在(y′,q′)∈M⊗AP⊕Q，使得q=α′(q′)，y=β′(q′)+(Id⊗α)(y′);

(vii) 若(s,t)∈HomA(P,N)⊕HomB(Q,B)，满足sα+(Id⊗t)β=0，tα′=0， 则存在(s′,t′)∈HomA(P,N)⊕HomB(Q,B)，使得s=s′α+(Id⊗t′)β，t=t′α′;

(viii) 若(u,v)∈HomA(P,A)⊕HomB(Q,M)，满足vα′+(Id⊗u)β′=0，uα=0，则存在(u′,v′)∈HomA(P,A)⊕HomB(Q,M)，使得v=v′α′+(Id⊗u′)β′，u=u′α．

定理1给定6元组(P,Q,α,β,α′,β′)，若其满足条件 (i)～(viii)，则

(2)

是强完全Δ(0,0)-投射分解．反过来，任何强完全Δ(0,0)-投射分解都具有(2)式的形式，其中X和f由(1)给出，并且满足条件(i)～(viii)．

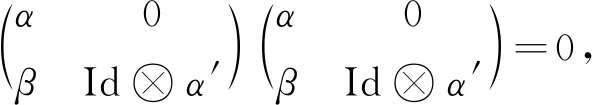
利用伴随对(TA,UA)，(TB,UB)[8]，可知

HomA(P,A)⊕HomB(Q,M⊗AA)≅

HomA(P,A)⊕HomB(Q,M).

令Y:=HomA(P,A)⊕HomB(Q,M)，由条件(i)，(ii)和(iv)可知序列

是一个复形, 其中

σ(u,v)=(uα,vα′+(Id⊗u)β′)，∀(u,v)∈HomA(P,A)⊕HomB(Q,M).

由条件(viii)可知它是正合列,这就说明了HomA(X·,(A,M⊗AA, Id,0))正合．再次利用伴随对(TA,UA)，(TB,UB)，可知

HomA(P,N⊗BB)⊕HomB(Q,B)≅HomA(P,N)⊕HomB(Q,B).

令Z:=HomA(P,N)⊕HomB(Q,B), 由条件(i)～(iii)可知，序列

是一个复形, 其中

ω(s,t)=(sα+(Id⊗t)β,tα′),∀(s,t)∈HomA(P,N)⊕HomB(Q,B),

进一步由(vii)可知它是正合列，即HomA(X·,(N⊗B,B,0,Id))正合．由于

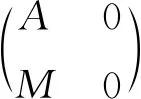
由此得到(γ,β′):(N⊗BQ,Q,0,Id)→(P,M⊗AP,Id,0)．根据Δ(0,0)-Mod中态射的定义即知下图交换

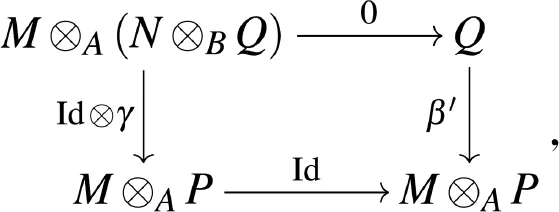
因此γ=0，否则上述图表不交换．类似地，由

(β,γ′):(P,M⊗AP,Id,0)→(N⊗BQ,Q,0,Id),

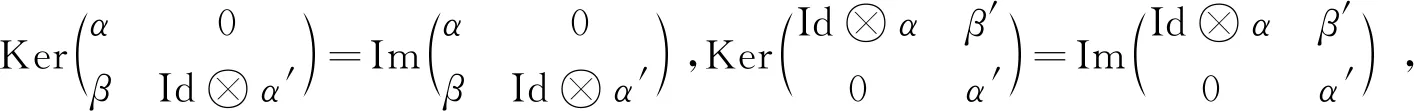
(SGProjA∩⊥N,M⊗ASGProjA∩⊥N):={(P,M⊗AP,Id,0)∈

{Δ(0,0)-mod|P∈(SGProjA∩⊥N)}.

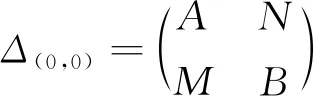
(1)S=(L,M⊗AL,Id,0)∈(SGProjA∩⊥N,M⊗A(SGProjA∩⊥N))，其中L具有强完全A-投射分解

并且Ker(Id⊗α)=M⊗AKerα.

(2)S=(N⊗K,K,0,Id)∈(N⊗B(SGProjB∩⊥M),SGProjB∩⊥M)，其中K具有强完全B-投射分解

并且Ker(Id⊗α′)=N⊗BKerα′．

(3)S=Kerf=({(p,x)∈P⊕N⊗BQ∣α(p)=0,β(p)+(Id⊗α′)(x)=0},

{(y,q)∈M⊗AP⊕Q∣α′(q)=0,β′(q)+(Id⊗α′)(y)=0})，

其中:f由(1)给出，P任意投射A-模，Q是任意投射B-模，并且α，β，α′，β′均满足条件(i)～(viii)．

证明令S=(L,M⊗AL,Id,0)∈(SGProjA∩⊥N,M⊗A(SGProjA∩⊥N))，其中L=Kerα∈SGProjA具有强完全A-投射分解

因为Ker(Id⊗α)=M⊗AKerα，所以序列

是正合列，因此序列

也是正合列，其中h=(α,Id⊗α)．注意到L∈⊥N意味着HomA(P·,N)是正合列，由P·的选取可知HomA(P·,A)正合．根据

HomΔ(0,0)(U·,(A,M⊗AA,Id,0))⊕(N⊗BB,B,0,Id)≅HomA(·,A)⊕HomA(·,N),

令S=(N⊗BK,K,0,Id)∈(N⊗B(SGProjB∩⊥M),SGProjB∩⊥M)，其中K=Kerα′∈SGProjA，其强完全B-投射分解为

由Ker(Id⊗α′)=N⊗BKerα′，可知序列

是正合列，从而序列

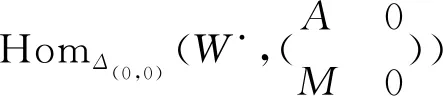
HomΔ(0,0)(W·,N⊗BB,B,0,Id)≅HomB(Q·,B),

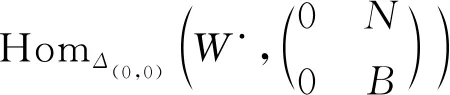
如果情形(3)成立，则由定理1知，序列

是强完全Δ(0,0)-投射分解，其中X由(1)给出．由此可知，S=Kerf是SG-投射Δ(0,0)-模．

接下来证明必要性．若S是SG-投射Δ(0,0)-模，则S=Kerf，其中f是在X·的强完全Δ(0,0)-投射分解中的Δ(0,0)-同态．由定理1，X·具有(2)式的形式，其中X和f由(1)给出，满足条件(i)～(viii)．

若在(1)式中取Q=0，则β=0，α′=0，β′=0．由条件(i),(v)和(viii)知

是强完全A-投射分解,由条件(vi)知Ker(Id⊗α)=M⊗Kerα,由条件(vii)知HomA(X·,N)正合，从而Kerα∈⊥N．于是

S=Kerf=(Kerα,Ker(Id⊗α))=(Kerα,M⊗Kerα)∈

(SGProjA∩⊥N,M⊗A(SGProjA∩⊥N)),

因此S具有(1)中的形式．

若在(1)式中取P=0，则α=0，β=0，β′=0．由条件(ii)，(vi)和(viii)知

是强完全B-投射分解，由条件(v)知Ker(Id⊗α′)=N⊗Kerα′，由条件(viii)知 HomB(X·,M)也正合，从而Kerα′∈⊥M．于是

S=Kerf=(Ker(Id⊗α′),Kerα′)=(N⊗Kerα′,Kerα′)∈

(N⊗B(SGProjB∩⊥M),SGProjB∩⊥M),

因此S具有(2)中的形式．

若在(1)式中取P≠0且Q≠0，则由定理1知S具有(3)中的形式．定理获证．