基于支持向量机的红外光谱发射率计算方法
2020-06-01刘丰瑞王俊华
傅 莉,刘丰瑞,王俊华,宫 禹
(1.沈阳航空航天大学 自动化学院,沈阳 110136;2.沈阳飞机设计研究所,沈阳 110135)
红外辐射及其衍生的红外技术在军事、工业、农业、医疗甚至日常生活中都获得了广泛应用。其中光谱发射率是描述红外辐射特性的重要参数,其体现了材料表面的光谱辐射能力,在光学测量诊断辐射传热效率分析中起到了关键作用,应用于辐射测温、红外加热、遥感遥测、能源动力、航空航天等领域中的新型高温、超高温材料。同时,光谱发射率也在国防、医学等领域具有重要的应用价值[1]。早在18世纪,人们就已着手开始研究物体表面的辐射特性。1753年富兰克林就提出不同的物质具有不同的接受和发散热量能力。几百年来人们依据这一经典理论,在理论、实验与工程实践中做了大量的研究性工作。随着红外技术、辐射传热学、太阳能研究、材料科学及黑体空腔理论等的进步与发展[2],近五十年以来,测量物体表面发射率的技术有了大幅提高。目前国内外发射率的测量方法主要有以下几种:量热法、反射率法、辐射能量法、混合法。虽然目前在国际上技术已经成熟,对于不同状态与温度下的物体,采用的测试方法与装置也不尽相同。然而,这并不能代表可以轻易对物体的表面发射率进行精确测量。同时,材料发射率还与表面粗糙度、所处环境和其表面温度息息相关。可以说物体的表面发射率是变化多端的,对其测量一直是个棘手而且难以解决的问题[3]。
红外辐射特性受到许多其它因素影响,因此,对被测物体进行红外辐射亮度建模时,各项变量之间的关系难以确定。通过红外辐射特性测试可以采集相应的观测数据样本,所以支持向量机对基于光谱辐射计的辐射亮度建模和计算研究极具价值[4]。结合目标红外辐射影响因素,从光谱辐射计测试的数据中分割出有效样本或波段,训练神经网络建立具有良好精度的亮度谱模型[5]。
1 光谱发射率测量原理
由于我们测量的物体类似于朗伯体,即发射率与方向无关,可表示为
(1)
式中,λ为波长,T为目标温度;M(λ,T),L(λ,T)为目标在温度T时的光谱辐出度和光谱辐射亮度;Mbb(λ,T),Lbb(λ,T)为相同条件下标准黑体的光谱辐出度和光谱辐射亮度。由式(1)可得,计算物体在此温度下的光谱发射率,只需求出同温度下物体的光谱辐射亮度和标准黑体的光谱辐射亮度。下面利用普朗克辐射定律建立一个标准黑体模型[6]。黑体的光谱辐射亮度Lbb(λ,T)的表达式由普朗克辐射定律表达为
(2)
式中,Lbb(λ,T)是黑体的光谱辐射亮度(w/(m2·μM));λ是波长(μm);T是绝对温度(K);e是光速(m/s);k是玻尔兹曼常数(W·s/k);c1是第一辐射常数,c2是第二辐射常数[7-8];
c1=2πhc2=(3.7415±0.0003)×108(W·μm4/m2)
(3)
c2=hc/k=(1.43879±0.00019)×104(μm·K)
(4)
2 支持向量机网络建模
2.1 支持向量机神经网络概述
支持向量机(Support Vector Machine,SVM)的其早期研究来自前苏联学者Vapnik在1963年发表的成果,类似于多层感知器网络和径向基函数网络,其主要思想是最大化存在于一个决策曲面当中的正例和反例之间的间隔边缘。这一决策曲面是由一个分类超平面建立的。直白地讲,统计学习理论就是支持向量机的理论基础;更精确地说,结构风险最小化的近似实现是支持向量机的精髓。支持向量机不需要利用问题的内部领域,同样能够在模式分类问题上提供良好的泛化性能。支持向量机(SVM)不仅适用于回归问题,在人像识别、文本分类等模式识别问题中也得到应用,引起了国内外许多专家与学者的关注与研究。与此同时,随着方法的改进与提出更优策略,支持向量机的性能也在不断提升。其应用范围也愈发广泛,重要性同样愈发凸显。
支持向量机具有以下的优点:
(1)应用于各种函数集;
(2)具有鲁棒性;
(3)总是能够有效地解决问题,属于最好的方法之一;
(4)利用简单的优化技术即可实现;
(5)基于VC推广性理论的框架,较为完善。
支持向量机的结构如图1所示。

图1 支持向量机的结构
其中K为核函数,其种类主要有:
①线性和函数:K(x,xi)=xTxi;
②多项和函数:K(x,xi)=(γxTxi+r)p,γ>0;
③径向基和函数:K(x,xi)=exp(-γ‖x-xi‖2),γ>0;
④两层感知器核函数:K(x,xi)=tanh(γxTxi+r)。
2.2 二分类与多分类支持向量机
2.2.1 二分类支持向量机
二分类支持向量机模型当中,C-SVC模型比较常见,其具体形式如下:
(1)设已知训练集
T={(x1,y1),…,(xl,yl)}∈(X×Y)l
其中,xi∈X=Rn,yI∈Y={1,-1}(i=1,2,…,l);xi为特征向量。
(2)选取适当的核函数K(x,x′)和适当的参数C,构造并求解最优化问题

(4)构造决策函数
2.2.2 多分类支持向量机
二值分类问题是SVM算法设计的初衷,而多类分类器则用来解决遇到的多类分类问题。目前,有两种主流方法:一类是直接法,顾名思义,就是直接作用于目标函数对其进行修改,只通过求解该最优化问题实现多类分类。这种方法看似不难,但由于计算的复杂性,只可适用于小型问题的解决。另一类是间接法,该方法是现阶段比较常用的,常见的方法有一对多和一对一两种。
(1)一对多(one-versus-rest)法:训练时依次把训练样本按类别归类,这样k个类别的样本就构出了k个SVM分类。如果样本类型未知,分类时将其归类为最大分类函数值。
(2)一对一(one-versus-one)法:其做法是在任意两类样本之间设计一个SVM,因此k个类别样本就需要设计k(k-1)/2个SVM。如果样本类别未知,最后得票最多的类别即为该未知样本的类别。
3 光谱发射率的计算与验证
本文选取某型号黑体辐射源(有效发射率:0.98,温度控制精度:0.1 ℃)作为被测目标,实验采用加拿大ABB BOMEN的MR170型光谱辐射计,液氮制冷,光谱分辨率为1~32 cm-1,InSb探测器光谱范围为2.0~5.5 μm,MCT探测器为4.0~15 μm。为了减少环境因素带来的误差,选择在尽可能黑暗的室内环境中对目标物体进行短距离测量[9-11]。
具体操作步骤如下:
(1)首先对辐射计进行标定。设定一个高温值和一个低温值,从而对仪器的响应度进行校准:将黑体(HFY-300A)的温度分别升至170 ℃和190 ℃,放在离辐射计4.92 m处,用辐射计测量这两个温度下的黑体光谱辐射亮度。
(2)用标定过的辐射计测量温度为180℃的隐身涂料钢板光谱辐射亮度,钢板如图2所示。
(3)因为黑体严格遵守朗伯体定律,所以根据上述公式与测量数据,进行支持向量机建模,计算得到目标的发射率。
3.1 光谱发射率计算
从测量的目标红外辐射亮度数据中任意选取300组数据作为训练样本,部分样本数据如表1所示。利用所建立的SVM神经网络模型对测量实验样本进行建模并计算辐射亮度,得到3~5 μm和8~12 μm波段的辐射亮度曲线,如图3所示。图中虚线为目标辐射亮度曲线,实线为SVM神经网络输出辐射亮度曲线。其中,在波长为4.3 μm左右存在数据波动,原因是物体辐射能量在传输过程中会受到大气影响,导致曲线有所波动。在其他波段,网络输出与实际值曲线比较吻合。

图2 隐身涂料钢板

表1 部分样本数据

图3 红外辐射亮度网络输出与实际输出
将SVM神经网络输出的目标物体辐射亮度数据与同等黑体的辐射亮度数据带入公式(1)可得到目标物体的光谱发射率如图4所示。本文所采用的黑体发射率为0.98,所以从图4中可以看出,目标物体的光谱发射率在波长为9.5 μm时误差最大,此波长所对应的发射率为0.997,最大相对误差为1.017%。
3.2 隐身涂料钢板发射率测量
利用上述方法,对飞机隐身涂料钢板的光谱发射率进行测量,计算其发射率,如图5所示。

图4 目标物体的光谱发射率
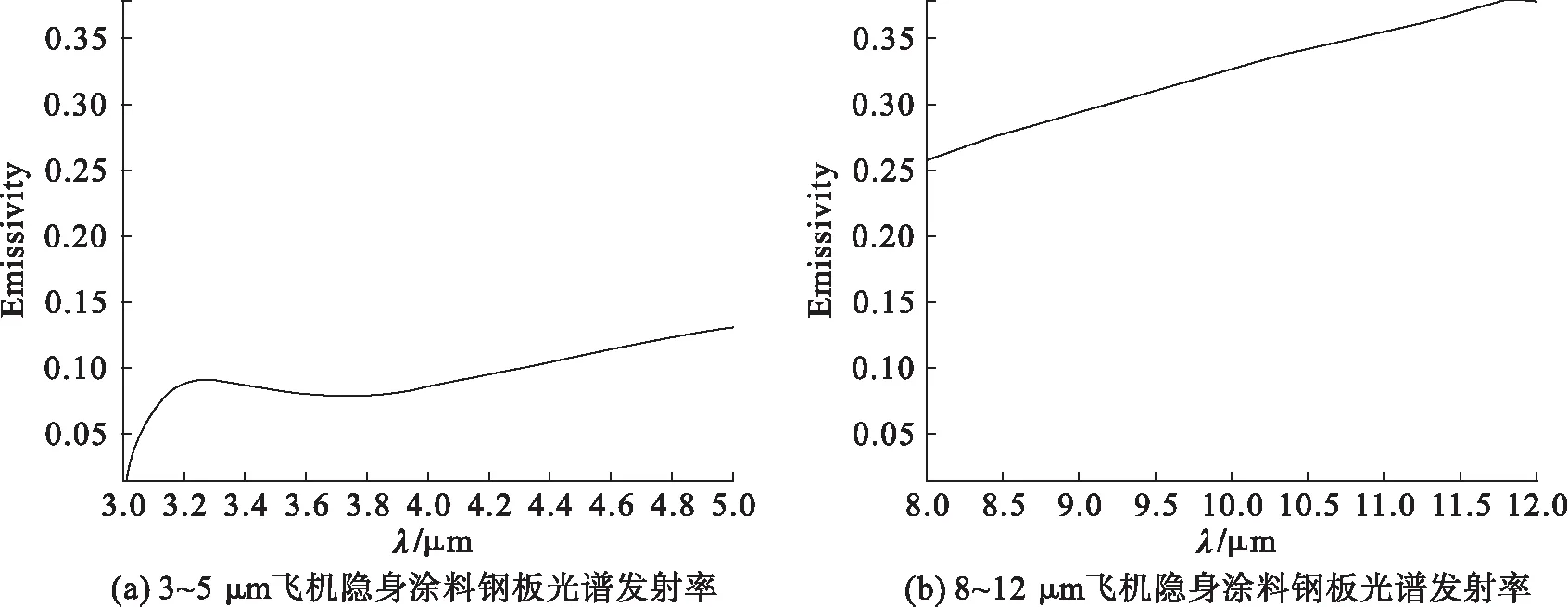
图5 飞机隐身涂料钢板光谱发射率
为了验证模型的准确性,利用维恩位移定律与普朗克公式
(5)
常数b1=1.1862×10-11(w/m2·μm·k5),c1,c2分别为第一、第二辐射常数,c1=3.743×10-16(w·m2),c2=1.439×10-12(m·k)。Mλmbb为理想黑体光谱辐射出射度的峰值,又有
(6)
式中,ελm为峰值处的光谱发射率;Lλ为目标辐射亮度峰值,则可得到目标温度177 ℃[12-15]。采用热敏电阻测量隐身涂料钢板表面温度为180 ℃,误差为3 ℃,证明本文所采用方法有效。
4 结论
本文采用SVM神经网络建立了红外辐射亮度模型,可以对大气等外在环境因素带来的干扰进行有效的消除,并对干扰波段进行辐射亮度估算。经过进一步计算,可以准确得到所测量目标的光谱发射率。通过对黑体的比对测试,验证了本文方法的有效性,并且将该方法用于飞机隐身涂料钢板的光谱发射率计算,最后通过热敏电阻(pt100)测量隐身涂料钢板的表面温度,从而验证了该方法的有效性。
(1)与标准黑体的发射率进行比对验证
通过对光谱发射率为0.98的标准黑体的红外辐射亮度估计,并计算出光谱发射率在9.5 μm时误差最大,此时计算所得到的光谱发射率为0.997,与标准黑体实际光谱发射率的最大相对误差为1.017%,该误差在误差允许范围之内,所以该方法是有效的。
(2)采用直接温度测量方法进一步验证模型准确性
由于隐身涂料钢板的光谱发射率未知,所以采用温度进行校核。利用本文所采用的方法计算出钢板的光谱发射率,最后得到钢板的表面温度为177 ℃,误差为1.016%,在误差允许范围内,所以该方法是有效的。
