基于多尺度量子熵的中介轴承声发射信号故障特征提取技术研究

刘丽丽，田 晶，刘广鑫，张 帅，田博文，艾延廷

(1.沈阳航空航天大学 航空发动机学院，沈阳 110136；2.空军装备部驻沈阳地区第一军事代表室，沈阳 110850；3.中国人民解放军93318部队，辽宁 铁岭 112300)

现代多转子航空发动机普遍采用中介轴承支撑方案，中介轴承通常位于高压转子的后支点支撑在低压轴上，或低压轴支承在高压转子的内腔中，轴承的外环和内环分别随高压转子和低压转子旋转。中介轴承的工作环境极其恶劣，容易出现故障，一旦出现微小故障将会引起转子的振动幅度加大，甚至造成转子瞬间停转,进而导致发动机停车，因此对中介轴承进行状态检测和故障诊断十分重要[1-2]。

中介轴承故障信号微弱，容易淹没在噪声中，不易提取到有效的故障特征。由于振动信号的干扰源较多，对早期故障不敏感等缺点，所以本文提出基于声发射信号的故障诊断研究。声发射信号具有高频特性，有很高的灵敏度，容易提取到有效的中介轴承的早期故障信号特征[3-4]。

基于熵值理论的分析方法可以不经过信号的变换或分解，直接度量信号的复杂度，完成轴承不同故障位置的识别。目前，常用的熵值是样本熵和排列熵。然而，样本熵对于大数据的计算效率较低，而排列熵虽然能提高计算效率，但是对噪声过于敏感，不能够有效地提取到轴承故障信息[5]。近似熵、样本熵和模糊熵只能从单一尺度上度量时间序列复杂性，与复杂度之间没有直接对应关系。Costa等[6]提出了多尺度熵概念，首先对时间序列进行空间尺度分割，然后计算每个尺度下样本的熵值，进而得到时间序列在不同尺度下的复杂度。郑近德[7]将粗粒分割与模糊熵相结合提出多尺度模糊熵，并将其应用于轴承不同故障类型的诊断中。

近些年来，量子理论广泛应用于各种领域，是一种有效的信息处理工具，其特有的信号描述方法可表达出信号的瞬时状态，使信号的局部特征得到量化[8]。本文将文献[9]的相关内容与信息熵理论相结合并且加以改进，提出一种基于多尺度量子熵的特征提取方法。

1 声发射信号的多量子位系统

在计算机中比特是最基本的储存单位，在量子理论中，量子比特是其最基本的单位。最简单的量子比特可以理解成一个双稳态系统，他是由两种量子态的线性叠加所组成。其数学形式可以表达为[10]

|φ〉=a|0〉+b|1〉

(1)

其中，a，b是满足|a|2+|b|2=1的实数或复数，称为概率幅。|a|2、|b|2分别表示量子比特|0〉、|1〉两个基态出现的概率。|0〉和|1〉为量子比特的量子基态。

设声发射信号为X={x(i),i=1,2,…,N}，共有N个采样点元素组成，使用下式对信号的每个采样点元素x(i)进行归一化处理，得到y(i)∈[0,1]。

(2)

根据文献[9]提出的振动信号非线性量子表达的公式，本文提出将声发射信号从时域空间映射到量子空间，用于分析声发射信号的状态。归一化后的声发射信号线性量子表达式为

(3)

将声发射信号的每个采样点都用量子比特来描述，第i个量子位的状态为|φi〉=ai|0〉+bi|1〉，则可用k个单量子比特的直积态表示该声发射信号的瞬时状态[10]

(4)

式(4)中，|ib〉表示含k个量子比特的量子系统|Yk〉的第i基态，为二进制表达形式。根据量子理论的归一化条件，概率应满足

(5)

量子理论用|0〉、|1〉分别代表声发射信号中的最小值和最大值两种状态，由于故障轴承在旋转时，会产生声发射信号，因此|010〉可用来表示峰值，则|ωi|2表示存在波峰的可能性大小。同理，如果基态|ib〉中包含|101〉，则说明可能存在波谷信息，|ωi|2则表示存在波谷可能性的大小。

取声发射信号X中相邻3个采样点X={x(i-1),x(i),x(i+1)}，对序列进行归一化得到Y={y(i-1),y(i),y(i+1)}，用量子比特描述可表示为

|y(i-1)y(i)y(i+1)〉=

(6)

2 多尺度量子熵

2.1 量子信息熵基本原理

信息熵是对系统不确定性程度的描述，因此可以用信息熵对轴承运行状态的变化情况进行度量。系统信息熵的定义为

(7)

式(7)中，u(Ai)为集合Ai的测度，i=1,2,…,n。

信息熵与量子理论中使用各量子基态或矢态及其出现的概率表达信息状态的方法非常相似，因此可将量子理论与信息熵相结合来描述中介轴承的运行状态。根据可行性分析并结合样本熵、排列熵等信息熵的原理，量子信息熵的基本原理如下：

(1)信号归一化

设声发射信号时间序列X={x(i),i=1,2,…,N}，根据公式对声发射信号时间序列进行归一化，归一化后的时间序列为Y={y(i),i=1,2,…,N}。

(2)相空间重构

根据文献[10]对归一化后的时间序列进行相空间重构，得到矩阵Y0

(8)

式(8)中，j=1,2,…,K，m为嵌入维数，λ为延迟时间，K=N-(m-1)λ，其中Y0(j)称为重构分量。

(3)重构分量的量子化

(9)

式(9)中，|ib〉为重构分量|Y0(j)〉量子系统的第i个态矢,ωj,K为态矢|ib〉概率幅值，|ωj,K|2态矢|ib〉的概率,其满足归一化条件。

(4)计算各态矢概率

(10)

式(10)中，K=1,2,…,n。

(5)计算量子信息熵

将各态矢出现的概率作为事件出现的概率，计算信息熵

(11)

(6)量子信息熵归一化

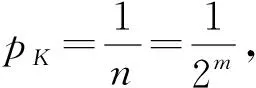
(12)

标准化后满足0≤Hq(X)≤1。

根据Shannon信息熵概念，量子信息熵Hq(X)表示时间序列X量子化后各矢态的概率分布。Hq(X)越大，代表各矢态的概率分布越均匀，即各矢态出现的概率越接近；反之，Hq(X)越小，代表各矢态出现的概率相差越大。

2.2 多尺度熵

在2002年，Costa等人[6]首次提出一种基于样本熵、用来分析有关时间序列复杂程度的重要度量方法——多尺度熵(Multiscale Entropy，MSE)。该方法很好地解决了样本熵算法尺度单一的缺陷，多尺度熵是在样本熵的计算方法基础上的改进，研究推得其计算过程如下。

设N点离散时间序列为X={x(i),1≤i≤N}，在给定的嵌入维数m和相似容限r之下，构建新的粗粒化向量。可得其数学公式如下

(13)

式(13)中，τ为尺度因子τ=1,2,…,n，n为正整数。

(2)求取每一个粗粒向量的样本熵，并将得到的n个粗粒向量样本熵的值表示成尺度因子的函数，如公式(14)所示

(14)

式(14)中，相似容限r=(0.1～0.25)*Std，其中Std为原始序列x(i)的标准差。

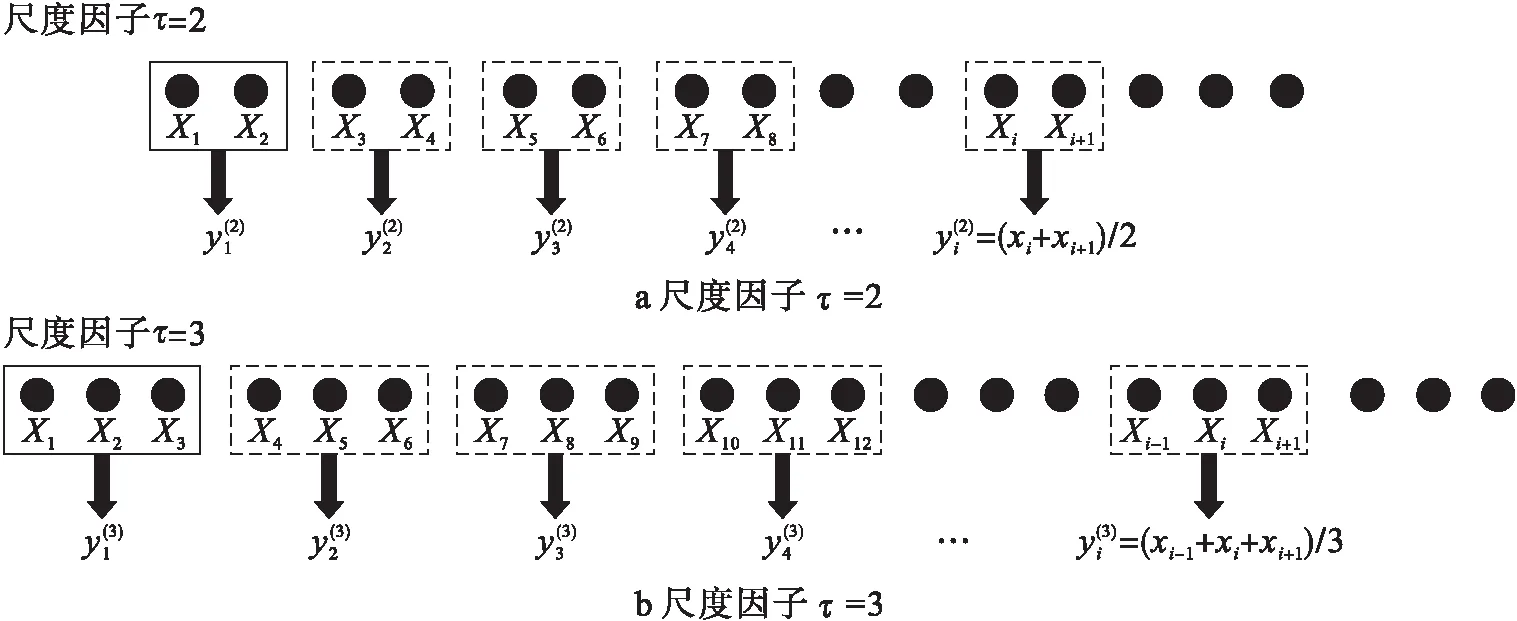
图1 粗粒化过程示意图

2.3 多尺度量子熵基本原理

通过公式(14)计算每个尺度因子下的粗粒向量的量子熵值，并构建带有尺度因子τ的函数，称为多尺度量子熵(Multiscale Quantum Entropy，MQE)。

(15)

2.4 多尺度量子熵的参数讨论

MQE总共有3个参数：嵌入维数m、时间延迟λ和尺度因子τ。由于参数取值的不同会影响最终的熵值[11]，因此需要讨论MQE参数的取值问题。

(1)嵌入维数m

嵌入维数m会影响序列重构后信息量的大小。m取值越大计算数据量越大，计算时间也越长，对原始数据长度N要求越大，通常原始数据长度N需要满足N=10m～30m。

(2)尺度因子τ

尺度因子τ决定了对原始序列进行多少个尺度的分割，本文设定尺度因子为τ=10。

(3)时间延迟λ

时间延迟λ对熵值计算的影响较小[12]，一般取λ=1。

3 在中介轴承特征提取中的应用

为了检验多尺度量子熵在中介轴承特征提取中的应用效果，本文通过中介轴承故障模拟试验台采集声发射信号验证其实用性。

3.1 中介轴承故障模拟试验

为验证多尺度量子熵在轴承特征提取中的有效性，针对型号为NU202的圆柱滚子中介轴承进行故障模拟实验。在不同转速的情况下，模拟了中介轴承外圈故障、滚动体故障、内圈故障，并与正常状态进行了对比分析。

中介轴承安装在双转子试验台上，试验系统如图2所示。采用Express-8声发射系统进行声发射信号采集与分析，在轴承座的径向布置声发射传感器，传感器的位置如图3所示。轴承内外圈旋转方向为反向，每种类型进行了20次实验，即每一种故障类型有20个样本，4种类型轴承共计80个样本，每个样本采集10 s。轴承故障的声发射信号为高频信号，一般在50 kHz以上[13]，根据香农采样定理，本试验采样频率设置为1 MHz。

图2 中介轴承故障模拟试验台

3.2 试验数据分析

在内圈转速为1 000 r/min、外圈转速为600 r/min时，4种状态采集到的声发射信号时频图如图4所示。由此4种状态的时域和频域波形可知，其各状态下的频率成分十分复杂，且相差甚微，故障信息被淹没，仅根据此时频域分析很难判断中介轴承的运行状态。

图3 声发射传感器位置图

图4 中介轴承4种状态下的时域和频域波形

使用本文提出的多尺度量子熵对4种状态下的声发射信号提取特征。根据文献[14]中的参数优化方法，针对此4种状态，在相空间重构时，使用互信息法确定延迟时间为λ=1，使用伪邻近法确定嵌入维度m=6，计算4种状态下的多尺度量子熵。

不同尺度因子τ下的MQE特征量对中介轴承故障区分程度不同，为利于故障区分需选取最优尺度因子τ下的MQE特征量。

利用MATLAB编程计算中介轴承在不同尺度因子下的MQE值。同一尺度因子τ在不同故障状态的两两MQE特征量之差的平方和，记为Ss。Ss值越大，说明该尺度因子τ下的MQE特征量对不同故障的区分度越高[15],如表1所示。

表1 中介轴承MQE特征量及其Ss值

由表1可知，τ为6时的Ss值较大，所以选择τ为6下的MQE值作为故障区分时的特征分量。分别计算τ为3、4、6时80个样本的MQE值，计算结果图5、6、7所示。

图5 τ=3时中介轴承4种状态下声发射信号的多尺度量子熵

图6 τ=4时中介轴承4种状态下声发射信号的多尺度量子熵

图7 τ=6时中介轴承4种状态下声发射信号的多尺度量子熵

从图5、6、7可以看出，在不同尺度下，故障信号的量子熵的分离程度有着很大的差异。图5中内圈故障和外圈故障的量子熵曲线分离程度一般，滚动体故障与其他3种状态的量子熵曲线不能实现分离。从图6中可以看出4种状态下的量子熵曲线分离情况较图5有很大提升，但是效果仍不理想，不能将故障准确的识别出来。如图7所示，当选取最优特征时量子熵可以很好的分辨4种状态的信号，各状态下熵值不同且保持稳定，说明多尺度量子熵具有很好的效果。

3.3 与MPE和MWPE结果对比

为进一步说明多尺度量子熵在中介轴承特征提取中的优越性，本文使用多尺度排列熵(Multiscale Permutation Entropy,MPE)和多尺度置换熵(Multiscale Weight Permutation Entropy,MWPE)[16]提取4种状态下的中介轴承声发射信号特征，计算结果如图8、9所示。由图8、9可知，MPE和MWPE对中介轴承4种状态提取的特征波动较大，稳定性差且特征曲线未分离，所以并不能作为准确判断中介轴承运行状态的有效特征。相对于MPE和MWPE，本文提出的多尺度量子熵在判断中介轴承声发射信号特征提取中更有优势。

图8 中介轴承4种状态下声发射信号的多尺度排列熵

图9 中介轴承4种状态下声发射信号的多尺度置换熵

3.4 中介轴承转速特征提取

针对中介轴承外圈故障、内圈故障和滚动体故障，本文开展了故障模拟实验，中介轴承外圈转速设定为300 rpm，内圈转速分别设定为0 rpm、300 rpm、600 rpm、900 rpm。采用本文提出的多尺度量子熵提取故障信号，结果如图10～12所示。

图10 不同转速下外圈故障多尺度量子熵

图11 不同转速下内圈故障多尺度量子熵

通过对比分析可知，在不同转速下外圈故障、内圈故障及滚动体故障的熵值变化不大，因此多尺度量子熵对转速变化不敏感，不用考虑转速对多尺度量子熵值的影响。

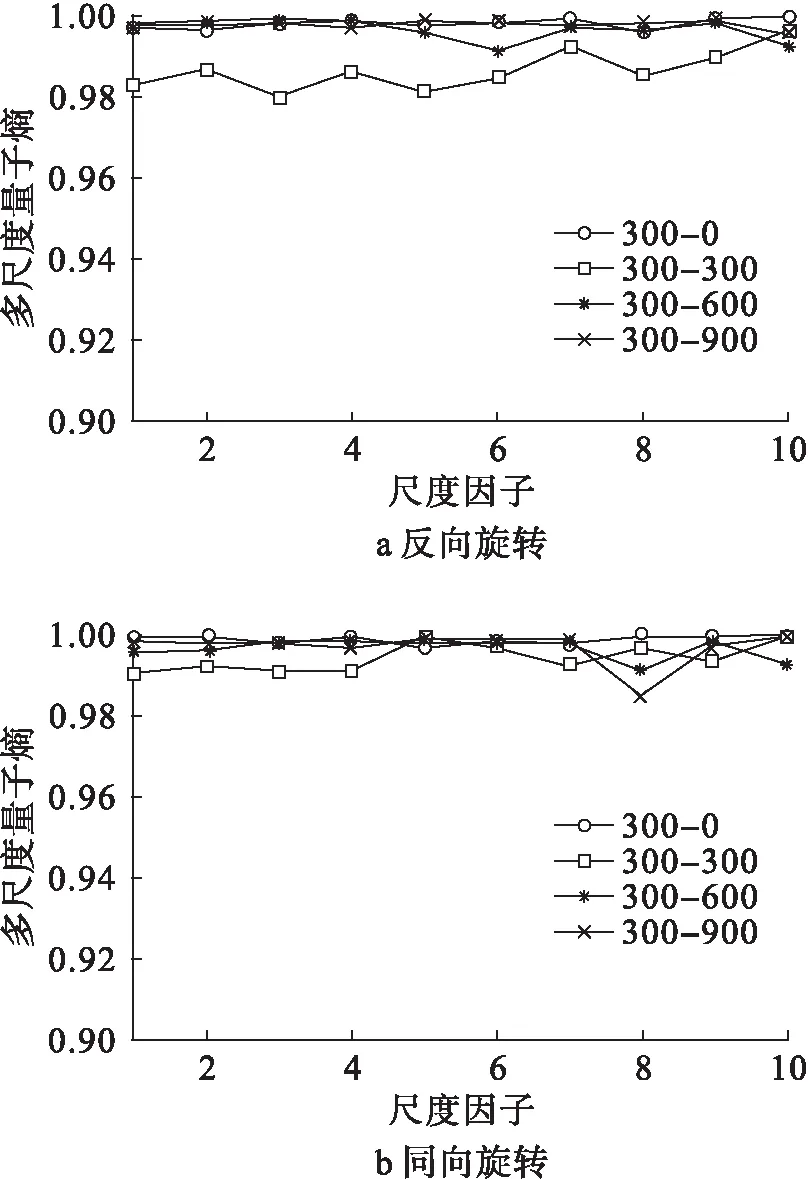
图12 不同转速下滚动体故障多尺度量子熵

3.5 结果分析

通过试验结果分析，针对中介轴承不同运行状态的声发射信号，多尺度量子熵具有很好的分析能力，根据图7所示，轴承正常时声发射信号具有最大的MQE值，说明其声发射信号对应的各态矢分布相对更均匀，而在故障后由于裂纹故障产生的频率变化及冲击对其声发射信号具有较大的影响，造成矢态分布变化，导致其MQE值减小。中介轴承在运动过程中声发射信号的多尺度量子熵值保持一定的统计规律，各状态下的态矢概率趋于稳定，且不同状态下的多尺度量子熵值不同。因此，多尺度量子熵可以作为判断中介轴承运行状态的特征。本章最后采用多尺度量子熵对不同转速的实验信号进行特征提取。结果表明，该算法对转速不敏感。

4 结论

(1)本文在量子熵的基础上提出了一种优化特征计算方法—多尺度量子熵。试验结果表明该方法可以用于中介轴承声发射信号的特征提取，进而判断中介轴承的运行状态。

(2)该方法原理简单，计算快捷，对于不同状态下的中介轴承具有很高的区分度，能够用于中介轴承的故障诊断。通过与MPE和MWPE对比可知，针对中介轴承声发射信号的特征提取，多尺度量子熵更为有效。

(3)多尺度量子熵作为一种全新的特征提取方法，对于算法中的延迟时间和嵌入维度等参数对其计算结果的影响和该方法在耦合故障中的效果还有待进一步研究。