下沉角速度对弹道的影响及算法研究

杨 芳

(1.西安航空学院 飞行器学院，西安 710077；2. 陆军工程大学 石家庄校区，石家庄 050003)

0 引言

轻型反坦克导弹作为精确制导武器，它是近距离攻击装甲车和坦克的主要武器之一。现代反坦克导弹通常采用发射筒倾斜发射，如“标枪”“长钉”“红箭-8”等[1-3]。对于从发射筒发射的导弹，当其前定向钮离开发射筒后，导弹会绕定向器约束的后定向钮转动，产生一个转动角度和转动角速度，即下沉角和下沉角速度[4]，而下沉角和下沉角速度对于弹道高度有着直接影响。轻型反坦克导弹受发射环境的制约，其出筒速度较低，若不对下沉角度加以控制势必对导弹的射击精度及可靠性等造成很大影响，所以必须要对其进行深入研究。

文献[5]给出了地面发射时火箭下沉量的计算方法，文献[6]建立了以不同滑离方式发射火箭的仿真模型，对某气象火箭在考虑下沉角及下沉角速度时的飞行轨迹进行了数值仿真。计算结果表明:下沉角及下沉角速度对气象火箭射高有一定影响。文献[7]对便携式红外寻防空导弹的初制导进行了定性研究，分别讨论了导弹发射出筒后提供前置角补偿和侧向力控制等方案来减小下沉角对弹道的影响。

本文分析了轻型反坦克导弹下沉角速度对弹道高度的影响，并对下沉角速度和指令攻角之间的关系进行了研究。研究结果表明：当下沉角速度不同时，为保证弹道射高一致性，其下沉角速度与指令攻角间会呈现线性关系。据此提出了通过初始下沉角速度插值指令攻角的自适应计算方法，利用这一方法解决了不同下沉角速度对弹道高度影响的问题，使导弹的末制导弹道具有较好的一致性，不但降低了控制系统复杂度，同时也提高了导弹命中精度。

1 导弹出筒段运动方程

1.1 约束期

导弹出筒段弹道包括两段，即约束期和半约束期的运动。对于没有定心部的导弹而言，约束期是指导弹质心在发射筒内的时间，半约束期是指导弹质心出筒到导弹完全出筒为止。约束期如图1所示。

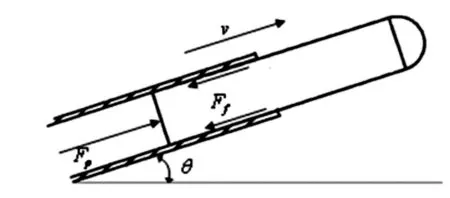
图1 约束期示意图

导弹受到发射筒的严格限制，只能沿着发射筒的方向运动，其运动方程如下：

其中，Fp为发动机推力；Ff为导弹与发射筒之间的摩擦力；θ为发射角；I为发动机比冲量；v为导弹速度。

图2 半约束期示意图

1.2 半约束期

半约束期如图2所示。

在半约束期内，由于导弹重心已经位于发射筒外，故导弹可绕质心转动。此时的导弹速度不高，故可忽略空气动力的影响。当只考虑重力作用时，半约束期内导弹运动方程如下：

φ=θ-φα(9)

2 弹道方案及制导方程

以某轻型反坦克导弹为例，其动力系统为双脉冲固体火箭发动机。内弹道从导弹的Ⅰ级脉冲发动机点火开始到导弹尾部离开发射筒为止，外弹道从导弹完全出筒至命中目标，其弹道具有下述典型飞行阶段。

(1)初始段：包括I级发动机点火后导弹在发射筒内运动阶段和出筒后无控飞行直至II级发动机点火所历经的弹道段。初始段运动的数学模型(纵向)：

(2)比例导引段：从比例导引段开始到进入导引头盲区。比例导引段运动的数学模型(纵向)：

其中比例导引段的弹道可通过改进的比例导引方法实现，如图3所示。

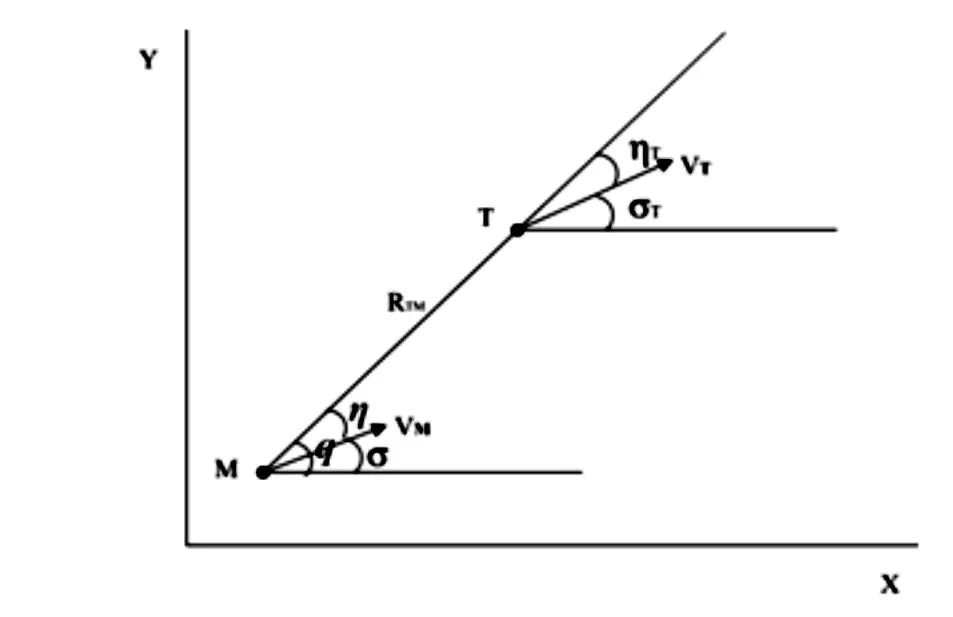
图3 弹目平面相对运动关系图

图3中，M点代表导弹，T点代表目标坦克，RTM为导弹与目标的距离；q为目标线方位角；σ、σT分别为导弹、目标速度矢量与基准线之间的夹角；η、ηT分别为导弹、目标速度矢量与目标线之间的夹角。

根据图3所示几何关系，以及弹目速度关系，得到弹目平面相对运动方程组为：

为了始终保持导弹速度矢量的旋转角速度与目标视线的旋转角速度成给定的比例关系，建立改进的比例导引关系方程为：

其中，θf为末端攻击角度；K比例导引纵向、横向导引系数；φcx为俯仰程序角。

3 下沉角速度对弹道影响

根据导弹出筒状态方程以及制导方程，利用Matlab仿真工具进行仿真计算。以2000m射程为例，得到导弹飞行高度曲线、俯仰姿态角曲线及攻角曲线，如图4～图6所示。

图4 高度随射程的变化曲线

从仿真曲线可以看出，当导弹的初始下沉量不同时，其导弹的飞行高度变化差异较大，越接近目标导弹的姿态变化越大，所受过载越大，这对导弹的控制系统控制效果极为不利，不但容易产生较大攻角，更会降低命中精度和毁伤效率，如表1结果所示。

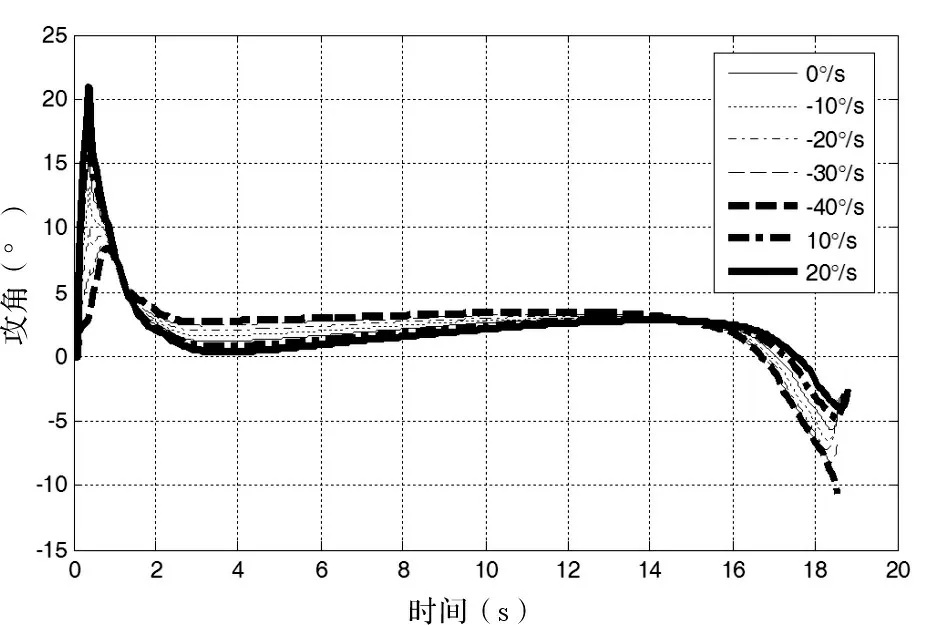
图6攻角随时间的变化曲线

表1 未用自适应插值法的弹道数据

当出筒下沉角速度为0°/s时，导弹能准确命中目标。但随着出筒下沉量的增加，命中精度受到影响。当出筒下沉量角速度为-40°/s时，落点偏差增为5.1m，此时落地攻角为-10.75°。由此看出，出筒下沉量对导弹命中精度具有一定影响。

为了使导弹在弹道末段具有较好的一致性，降低导弹的控制难度，因此在导弹的弹道初始段与比例导引段间增加了指令飞行段，目的是让导弹初始段结束后，通过指令攻角的控制，调整导弹飞行轨迹，尽快提升导弹的飞行高度。

(1)初始段：I级发动机点火后导弹在发射筒内运动阶段和出筒后无控飞行直至II级发动机点火所历经的弹道段；

(2)指令飞行段：初始段结束时刻至比例导引开始时刻，控制方程如下所示：

φcx(k)=φcx(k-1)+app·ΔT

φcx(0)=φcx(14)

其中φcx(k)为时刻的俯仰程序角，φcx(k-1)为上一采样点时刻的俯仰角，app指令攻角，ΔT为采样时间。

(3)比例导引段：从比例导引段开始到进入导引头盲区。

增加指令飞行段后，在保证导弹飞行最大高度的同时，建立了导弹出筒下沉角速度与指令攻角之间线性变化关系。利用导弹出筒后某一稳定状态时刻(0.4s)测得的下沉角速度作为指令攻角插值点，通过二维线性差值，完成弹道自适应解算，如表2所示。表2中ω04为导弹出筒稳定状态下沉角速度。

表2 下沉角速度与指令攻角差值表

将增加指令程序段的制导算法代入仿真程序中，仍以2000m射程为例，仿真结果如图7～图9所示。

从不同下沉角速度的弹道高度曲线对比来看(见图7)，增加了自适应计算方法后，飞行弹道对下沉角速度的变化变得不敏感了，其飞行最大弹道高度及末段的飞行轨迹基本相似，使得落点角度的一致性较好(见图8)，落点攻角小，且基本归零(见图9)。具体数据如表3所示。

图9攻角随时间的变化曲线

表3 增加自适应插值法的弹道数据

从表3可见，当出筒下沉角速度由20°/s变化至-40°/s时，导弹都能命中到目标，并且落地攻角都很小。通过这种自适应方法不但可以提高落点精度，同时也可以有效提高落点毁伤效力。

4 结论

倾斜发射的轻型反坦克导弹，下沉角和下沉角速度对于弹道高度有直接影响。本文分析了下沉角速度对弹道高度的影响，并对下沉角速度和指令攻角之间的关系进行了研究，找寻出下沉角速度与指令攻角间呈现线性关系的规律。利用导弹出筒后某一稳定状态时刻(0.4s)测得的下沉角速度作为指令攻角插值点，通过二维线性差值，完成弹道自适应解算。通过这一算法解决了不同下沉角速度(-40°/s～20°/s)对弹道高度影响的问题，使导弹的末制导弹道具有较好的一致性。这不但可以在导弹飞行末段降低控制系统复杂度，减小落地攻角，同时也将命中精度提高到1m以内。