连续钢桁梁桥墩顶起落梁法支座强迫位移影响研究

2020-05-31赵智航吴道洪周世军

水利与建筑工程学报 2020年2期

赵智航，吴道洪，周世军,3

(1.重庆大学土木工程学院，重庆 400045；2.中铁十二局集团第七工程有限公司，湖南长沙 410004；3.重庆大学山地城镇建设与新技术教育部重点实验室，重庆 400045)

在公铁两用桥[1-2]中，连续钢桁梁桥[3-4]是一种很有竞争力的桥型。目前，连续钢桁梁桥的施工大多数采用悬臂施工法[5-7]。但采用悬臂施工法的施工过程中存在两大难点：中跨合龙前的合龙口调整和合龙后的全桥线形调整。为克服这两个困难，目前大多数连续钢桁梁桥的合龙施工采用了以墩顶起落梁法[8-10]为主的合龙方案，即在支座处安装千斤顶，通过千斤顶的起顶和落顶对结构施加强迫位移，以调整钢桁梁的线形。

对于连续钢桁梁桥的墩顶起落梁调整方法，现有文献[11-14]侧重于报道施工技术，大多采用实桥有限元建模的方式取得调梁参数和评估施工效果，而对于连续钢桁梁桥起落梁法的关键参数——支座强迫位移量的计算方法研究较少，也较少分析结构体系转换后落梁施工对于连续钢桁梁线形和内力的影响，忽视了利用落梁步骤主动调整桥梁线形的潜力。

针对以上问题，本文结合某公铁两用连续钢桁梁桥的合龙施工实践，从刚体位移和矩阵位移法原理[15]出发，分别以合龙前合龙口闭合和落梁后的理想线形为目标，提出了体系转换前、后的目标支座强迫位移量的计算方法，并建立了基于施工过程的有限元模型，同时结合实测数据，对起落梁法的施工过程中的线形、内力和应力进行了分析，以说明本文提出的施工效果。

1 工程背景

某公铁两用桥主桥全长381 m，主桥结构为双线铁路双向6车道平行弦连续钢桁梁结构(孔跨布置为102 m+175 m+102 m)，公路桥面系使用辅助桁架加宽，钢桁梁截面呈倒梯形，典型横断面如图1所示。

图1 钢桁梁典型横断面布置图(单位：mm)

该桥采用两片竖直主桁作为主要承力结构，边跨主桁节间长度12.75 m，中跨12.50 m，全桥由30个节间组成，钢桁梁立面如图2所示。

图2 某公铁两用连续钢桁桥立面图(单位：m)

2 连续钢桁梁桥合龙施工的特点

该公铁两用连续钢桁梁桥的钢梁架设采用了边跨支架拼装，主跨全悬臂拼装，主跨中心合龙的施工方案，合龙示意图如图3所示。

图3 中跨合龙示意图

原施工方案在中跨设置了两个临时墩以减小中跨悬臂长度，方便跨中合龙。但由于该桥水道航运繁忙，为保证航道安全，取消了原设计中的临时支墩(如图3所示)。这一临时调整使得中跨悬臂长度大大增加，根据有限元计算结果，合龙口悬臂端竖向挠度约为-12 cm，比原设计施工方案下挠值增加35 cm，使得悬臂拼装线形控制和中跨合龙的难度大大增加。

如图4所示，由于合龙口变形过大，必须对合龙口进行调整，但该桥不具备设置合龙临时墩或临时扣索的施工条件，故采用了在支座安装强制纠偏装置，按照调梁→合龙→落梁的顺序进行合龙施工。该施工方法需要精确控制控制墩顶的强迫位移量，以保证落梁后的桥梁线形和内力符合设计要求。

图4 合龙口平面偏差示意图

3 目标支座位移量计算

3.1 合龙前调梁的目标支座位移量

在中跨合龙前，结构的体系为简支悬臂体系，此时支座处的强迫位移引起的是刚体位移，通过刚体位移公式可以计算支座竖向位移引起的合龙口的竖向位移和转角。这里以平面内的竖向偏差和转角偏差为例介绍简支悬臂梁的目标位移量的计算方法。

对于设计轴向为水平线的连续梁结构来说，可忽略竖向变形量的影响，将结构视为水平的梁进行计算。符号规定：竖向位移向上为正，转角位移顺时针为正。

如图5所示，当支座A、B分别发生竖向位移Δ1和Δ2的时候，悬臂端的平面内的竖向位移fy和转角位移α可以分别表示为:

(1)

(2)

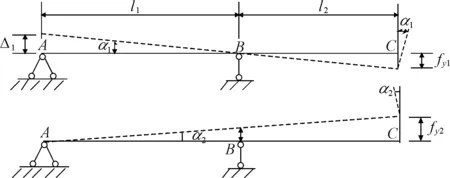
图5 刚体位移计算简图

当A、B支座同时发生位移时，悬臂端C的竖向位移和转角位移为:

(3)

从式(3)中可以解得目标支座位移量为:

(4)

平面外的刚体位移量计算方式类似，这里就不作赘述了。通过控制支座位移的量可以控制悬臂端合龙口的位移，使其达到合龙的要求。

3.2 合龙后落梁的目标支座位移量

当桥梁结构顺利在跨中合龙后，整体结构就由分立的静定简支悬臂状态转换为超静定的连续梁结构，此时落梁发生的支座位移将影响到结构的内力和线形。

根据矩阵位移法，结构的平衡方程可以表示为

K·s=f+r

(5)

(6)

该方程组中仅有s1和r2为未知量，其余量均为已知量，可解得s1和r2为

(7)

(8)

(9)

移项后可得:

(10)

K12·s2=b

(11)

比较该方程组的方程与未知量的个数，系数矩阵K12是一个n×m的矩阵，未知量列阵s2是一个m×1的向量。很明显，n>m，所以该方程组是一个超定方程组。一般来说，超定方程组无解(此时为矛盾方程组)，可以采用最小二乘法求其近似解。

在实际计算中，由于n>>m，采用最小二乘法需要求解的超定方程组为:

(12)

求解该方程是一件十分困难的工作，并且因为方程数量过多的缘故，最小二乘解的误差值往往会很大，因此必须降低方程的个数才能求得有意义的结果。实际上并不需要所有节点的位移值都接近理想水平，若某些处于关键位置节点的竖向位移达到理想水平，便可以基本判定全桥线形符合要求了。

假设三跨连续梁(如图6所示)的4个支座A、B、C、D处分别发生了单位位移，沿着梁长度方向取n个控制截面的竖向位移量作为研究对象，分别考察其在不同位置支座的单位位移下的位移量。

图6 连续梁支座位移计算简图

令由A、B、C、D支座处发生单位竖向位移引起的n个控制截面竖向位移量组成向量a,b,c,d分别为：

a={a1a2…an}

(13)

b={b1b2…bn}

(14)

c={c1c2…cn}

(15)

d={d1d2…dn}

(16)

由于此时的支座位移仍然属于小变形，结构仍然处于线弹性范围内，连续梁结构的位移满足线性叠加原理，则当4个支座分别发生δ1、δ2、δ3、δ4的位移时，则各个控制截面总的位移量{w}可以表示为:

w=δ1·a+δ2·b+δ3·c+δ4·d

(17)

若存在一个理想的控制截面位移量wL，则有方程组：

(18)

⟹(K·δ)=wL

(19)

此时m=4，n为主动选择的关键截面数量(如图6箭头所示)，通过选择不同数量的关键截面竖向位移的个数，可以大大降低方程的个数，极大地降低了求解的难度和误差量，为主动控制落梁位移值改善连续梁线形创造了基础。

4 桥梁安装线形和内力分析

根据该连续钢桁梁桥的施工步骤，采用桥梁施工分析软件CSFB建立了基于施工过程的有限元模型。

4.1 线形分析

桥梁合龙调梁前、调梁后、合龙后、落梁后、二期恒载后五个工况钢桁梁下弦节点相对拱度的理论计算值见图7，二次恒载后桥梁下弦节点的实测与理论相对拱度值见图8，用以说明施工线形控制的效果。

图7 下弦节点拱度有限元模拟结果

从图7中可以看到，合龙前的中跨合龙口处有0.1205 m的下挠以及约0.414°的相对转角。通过边墩落顶0.3 m，同时微调主墩顶升量的调梁操作，顺利消除了桥梁合龙口竖向偏差，在上挠0.3 m的高度顺利完成合龙，并且可以看到调梁前后桥梁线形形状基本不变，梁体仅发生了刚体转动。当体系转换后，支座落顶至指定位置，边跨线形基本回落至水平，中跨最大拱度降低至上挠0.1 m的位置。二期恒载加载后，全桥线形接近水平，施工控制达到了预期目标。

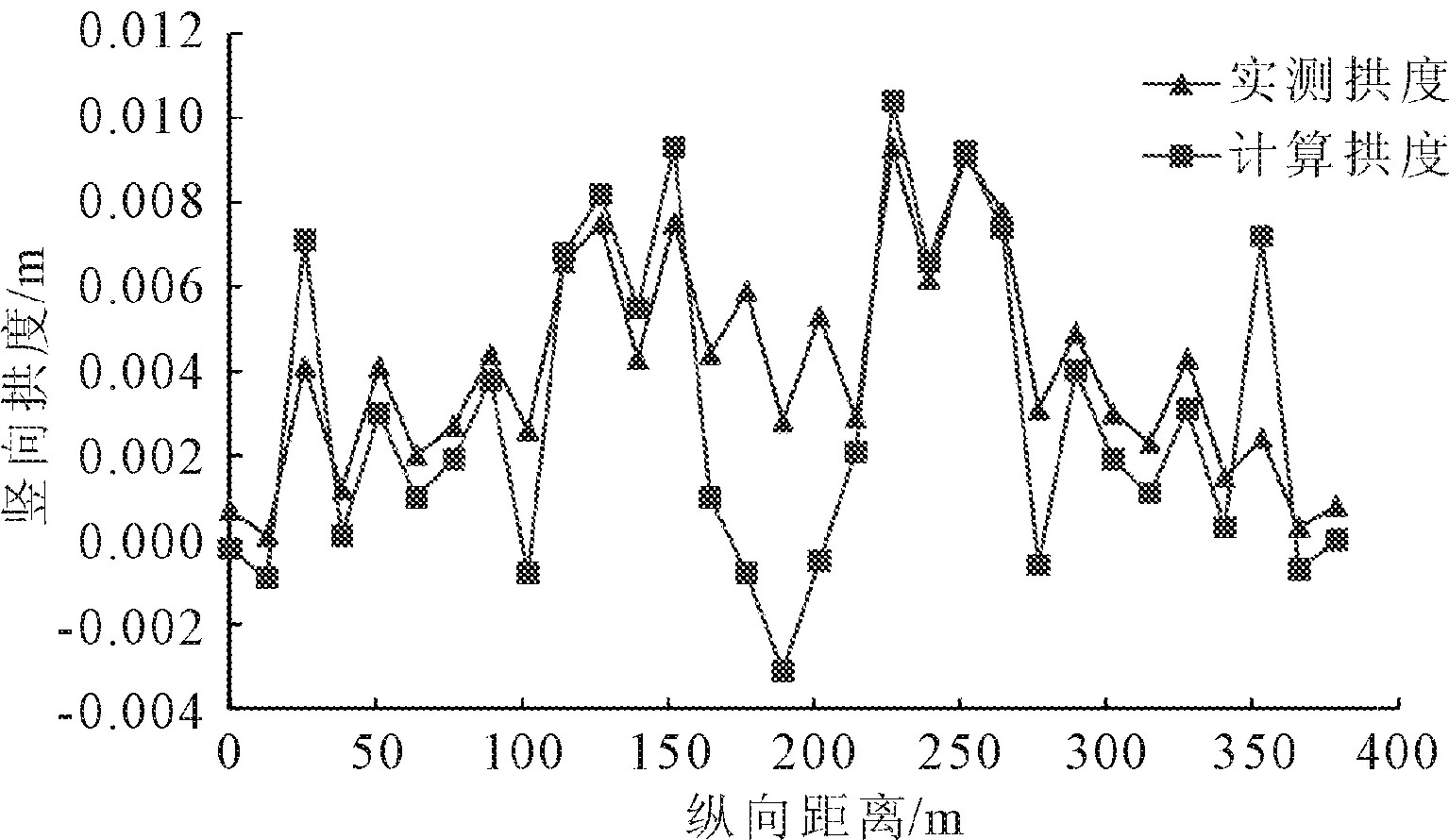
图8 二次恒载后全桥拱度曲线

从图8中可以看出，经过前述的调梁→合龙→落梁→二恒的施工过程，桥梁线形已经非常接近水平，最大拱度未超过1 cm，同时理论计算值与实测值也符合良好，仅在合龙口部分有约6 mm的偏差，其原因可能在于合龙口部件尺寸的微调以及安装时的偏差。

4.2 内力与应力分析

图9给出了该连续钢桁梁桥合龙后、落梁后和二期恒载后三个典型阶段的上弦杆、下弦杆、直腹杆和斜腹杆的轴力沿全长的变化曲线。合龙前、调梁后以及合龙后桥梁仅做刚体运动，对桥梁内力影响极小，这里以合龙后工况的轴力值为代表值。

首先比较合龙后与落梁后两个施工阶段杆件轴力分布。从图9(b)中可以看到，相比于合龙后工况，落梁后的上弦杆和下弦杆的轴力峰值显著降低，中墩附近的部分轴力转移至中跨，结构体系转换后的落梁强迫位移使得连续梁内部发生了明显的内力重分布。从图9(c)和图9(d)中可以看到，落梁的强迫位移对于直腹杆和斜腹杆轴力的影响并不显著，其分布规律未发生明显变化。其次，比较落梁后与二期恒载工况的轴力分布，可以发现二期恒载加载后的四个部位的杆件轴力都有明显增加，但分布规律基本一致。

合龙前、调梁后、合龙后、落梁前和成桥运营五个阶段的杆件最大应力值如表1所示。

表1 施工阶段杆件最大应力

从表1中可以看到合龙前、调梁后和合龙后三个阶段的杆件最大应力非常接近，结合桥梁的内力分布，证明合龙前调梁未影响结构内力状态。伴随着结构线形和内力分布的改善，落梁后工况杆件的最大拉、压应力分别也下降了42.35 MPa和33.95 MPa，结构的应力状态也得到了改善。虽然二期恒载加载后，结构的最大拉压应力上升到140 MPa左右，但是也在设计限值以内，可以保证结构的安全。