坡面降雨和坡脚浸泡对土坡影响的模型试验研究

王一冰，朱宝强，周 成，谭昌明，韩利彪

(1.四川大学 水利水电学院 水力学与山区河流开发保护国家重点实验室，四川 成都 610065；2.四川省公路规划勘察设计研究院有限公司， 四川 成都 610041)

我国地质地理条件复杂，气候条件时空差异大，是突发性地质灾害(滑坡、崩塌、泥石流等)多发的国家。据突发性地质灾害的分类统计，我国90%的滑坡由大气降雨直接诱发或与气象因素相关。而第四系松散堆积层因其强度低等特点，易发生降雨型滑坡，如我国福建地区每年台风暴雨季期间都会有大量的滑坡发生[1]。因此，研究降雨条件下土质边坡的变形破坏机理对防灾减灾具有重要的现实意义。

国内外学者利用有限元方法广泛开展了针对降雨边坡的水土特性和变形破坏的研究[2-6]，得出了不同降雨模式下土坡的破坏特征。还有一些学者开展了一系列的土坡降雨模型试验研究，利用较大尺寸的边坡模型，陈宇龙等[7]试验研究了堆积体土坡在降雨条件下渗流、变形和破坏的规律, 并引入声发射作为预警的判据；Ram等[8]针对砂土边坡的研究结果表明，降雨强度与滑动起始时间、初始滑移面位置之间存在一定的关系。利用小型土坡模型试验，许旭堂等[9]以降雨时间、坡度和坡土密实度为变量，分析了雨水入渗对坡土变形和吸力的影响，揭示了降雨诱发土坡失稳的破坏模式；Wu等[10]试验证实了松散土坡中孔隙水压力、含水率和边坡裂隙对边坡滑动失稳产生很大影响。利用离心模型试验，詹良通等[11]研究了降雨诱发粉土边坡的失稳模式，并获得了降雨强度与边坡失稳时降雨历时的关系数据；梁树等[12]试验揭示了降雨入渗对膨胀土边坡的影响。

长时间降雨导致坡脚水位上升，坡脚在水的浸泡作用下崩解破坏，也将威胁边坡稳定。利用土坡模型试验，江强强等[13]发现水位升降过程对边坡滑动影响程度不同，滑坡的失稳模式为牵引式滑坡；李子晗[14]分析了高水位长期浸泡作用下砂土堤防渗流场和水土压力的变化特征。利用离心模型试验，Zhang等[15]监测并总结了边坡的孔隙水压力、土压力、变形和演化特征；林葎等[16]发现水位变动条件下粉质黏土边坡的中下部首先形成局部破裂面，并逐步向上发展至坡顶形成完整滑裂面；苗发盛等[17]揭示了三峡岸坡水位变动条件下坡体位移和孔压等的变化规律。

我国南方地区存在大量由无黏性土回填形成的土坡，土坡稳定性与坡土抗剪强度关系紧密[18]，无黏性土的抗剪强度与降雨过程中土体含水率的变化有关，调查显示，降雨是无黏性土边坡最主要的触发因素之一。因此，对无黏性土边坡的水土特性和变形破坏规律的研究具有重要的理论意义和工程应用价值。另一方面，考虑到降雨后砂性土风干较快便于进行下一轮试验和便于坡土位移PIV观测(砂性土不粘槽壁)，因此本文试验选用砂性土模拟无黏性土坡，进行降雨滑坡机理的模拟研究。

本文开展砂性土边坡在降雨和坡脚浸泡条件下滑动破坏的框架式模型试验，利用体积含水率传感器测定了降雨条件下坡土不同深度和位置的含水率的变化特征，利用PIV技术揭示了边坡渐进变形和破坏的发展过程，分析了变形场特征，并进一步研究了长时间降雨坡脚浸泡导致的破坏规律。

1 坡面降雨和坡脚浸泡模型试验

采用模型试验模拟原型降雨滑坡，需要解决试验的相似率问题。其中几何相似一般土工模型试验容易满足，但很难做到满足应力相似，所以一般最好采用离心模型试验。本文选用框架式模型试验模拟降雨滑坡，和前人的土工模型试验一样，由于坡土较薄难以满足应力相似，因此只能采取近似满足应力水平(s=τ/τf)相似的做法，即采用人工降雨降低坡土的抗剪强度，从而使坡土的剪应力比上抗剪强度的值提高，研究土坡模型和原型相似的降雨破坏机理。

框架式模型试验是指在框架模型槽内用相似材料制作模型，在模型满足主要边界条件和几何相似以及应力水平近似的情况下测量坡土的变形和降雨饱和特性等数据，并利用这些数据揭示和阐明滑坡的发展机理。

1.1 坡面降雨模型试验

坡面降雨模型试验装置由框架式模型槽、降雨系统和数据采集系统三部分组成，如图1所示。试验模型槽长、宽、高分别为200 cm、50 cm、50 cm。槽侧面安装1 cm厚的有机玻璃板以便实时监测边坡变形情况，玻璃板内侧为打印有控制点的透明贴膜以便PIV系统确定控制点的精确坐标，槽底面铺设6 cm厚的硬质垫层以模拟基岩。由于滑坡概率随着坡度的增加而升高，考虑到降雨条件下边坡滑动的难易性，经过多次尝试，最终确定模型槽的坡度为20°，槽内坡积土相对模型槽底板的夹角为30°。

降雨模拟系统采用喷头式模拟系统，由喷头、供水管线和流量计三部分组成。模型边坡有效降雨面积约1 m2，流量计采用lzs-15型浮子流量计，可为试验边坡提供0～100 mm/ h的降雨强度。数据采集系统由位移测量系统和体积含水率传感器两部分组成。位移数据由PIV系统测得，试验过程中采用相机和计算机获取实时位移图像，利用GeoPIV程序处理滑坡图像，分析边坡土体位移场[19]。体积含水率传感器采用美国Decagon公司的EC5小型土壤水分传感器，该传感器由探针和壳体两部分组成，具有精度高、操作简便、适用范围广泛、防水能力强和对周围土体扰动小等优点。传感器埋设位置分别在坡脚下部10 cm(A点)、坡中上部10 cm(B点)、坡中下部20 cm(C点)和坡顶下部10 cm(D点)，如图1所示。

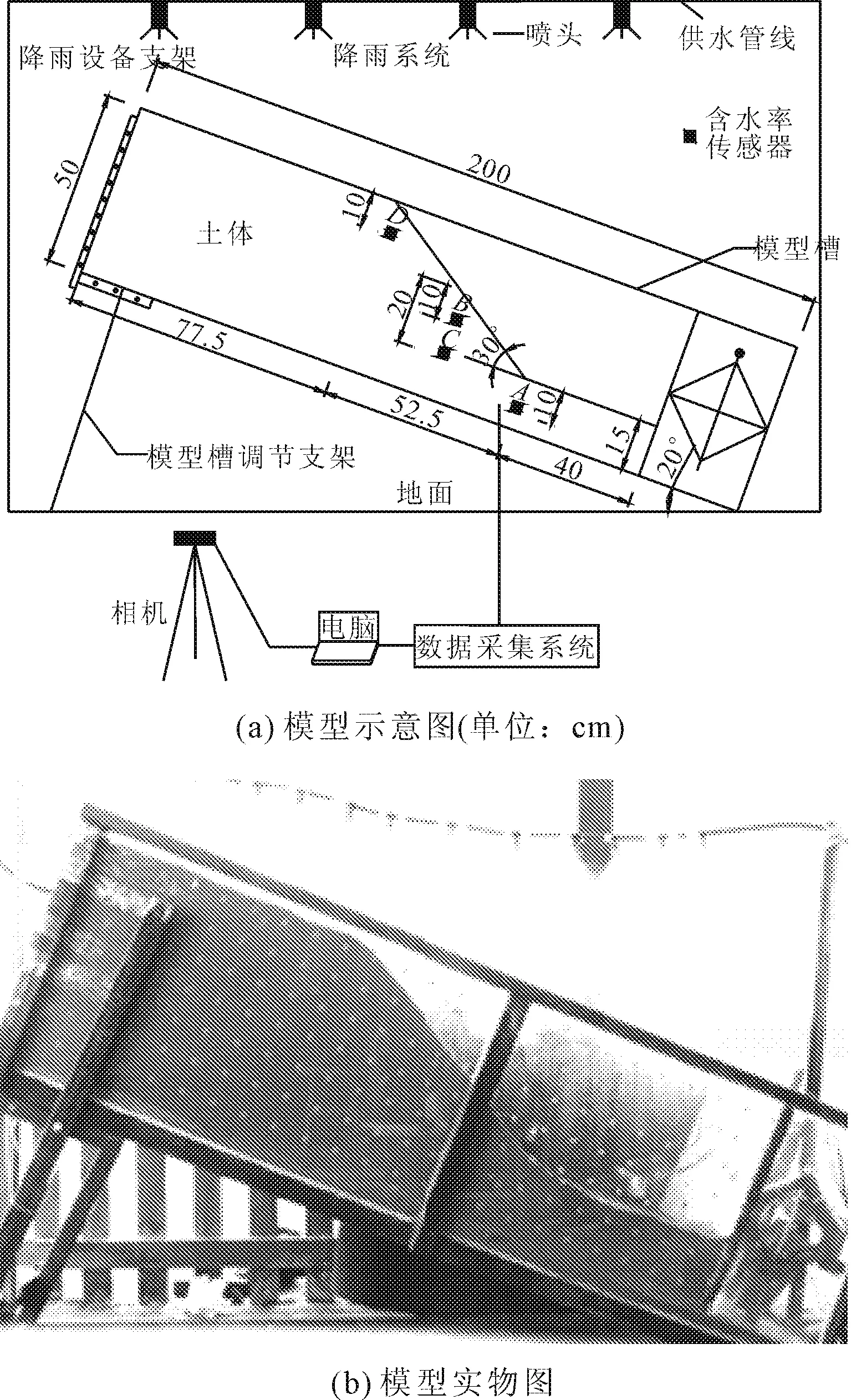
图1 坡面降雨模型试验装置图

由于试验中很难模拟真实气象条件下的波动型降雨历时过程，因此模型试验中的降雨过程设计采用恒值的人工降雨强度，通过控制降雨历时来设定降雨量。根据四川地区的经验，时降雨强度大于70 mm或日降雨强度超过200 mm时，滑坡灾害发生的概率将会明显增加。本文试验选定降雨强度为100 mm/h，降雨类型为持续平稳型降雨，试验降雨共持续6 h。

1.2 坡脚浸泡试验

为研究长时间降雨导致的坡脚浸泡问题，在坡面降雨模型试验的基础上，在模型槽右侧底部增加一个水槽蓄水，以模拟坡脚浸泡工况。设计水槽底长、顶长、宽、高分别为90 cm、65 cm、50 cm、45 cm。为方便观测和记录坡土的变形，在坡土与玻璃接触的表面位置注入条状有色土进行位移标记，坡脚浸泡模型如图3所示。考虑到坡脚浸泡工况下坡体底部无支撑，为保证边坡模型的顺利制作，槽内坡积土相对模型槽底板的夹角为15°。随后将模型槽坡度缓慢升至35°。

试验过程中用直径3 cm的塑料水管，以0.01 m3/ min的速度往水槽内蓄水，蓄水过程一共15 min，在此过程中用照相机记录坡土正面和侧面的变化过程。

图2 坡脚浸泡模型试验装置图

1.3 试验材料

为研究降雨条件下无黏性土边坡的变形破坏特征，选取砂性土作为试验用土，考虑到降雨条件下边坡滑动的难易性，经过多次尝试，确定模型边坡的填筑干密度控制为1.5 g/cm3，初始含水率控制为7%，其基本物理力学参数见表1。

表1 试验用砂性土的基本参数指标

2 试验结果与分析

2.1 坡面降雨试验结果与分析

(1) 坡土体积含水率随降雨历时的变化过程。将各测点的体积含水率随降雨历时的变化过程见图3，从图3可以看出，在降雨入渗的过程中，边坡内部各位置土体含水率都会出现不同程度的增长，最终达到一个稳定状态，据此可以将含水率变化过程大致分为三个阶段：初始平稳期、上升期和最终稳定期。

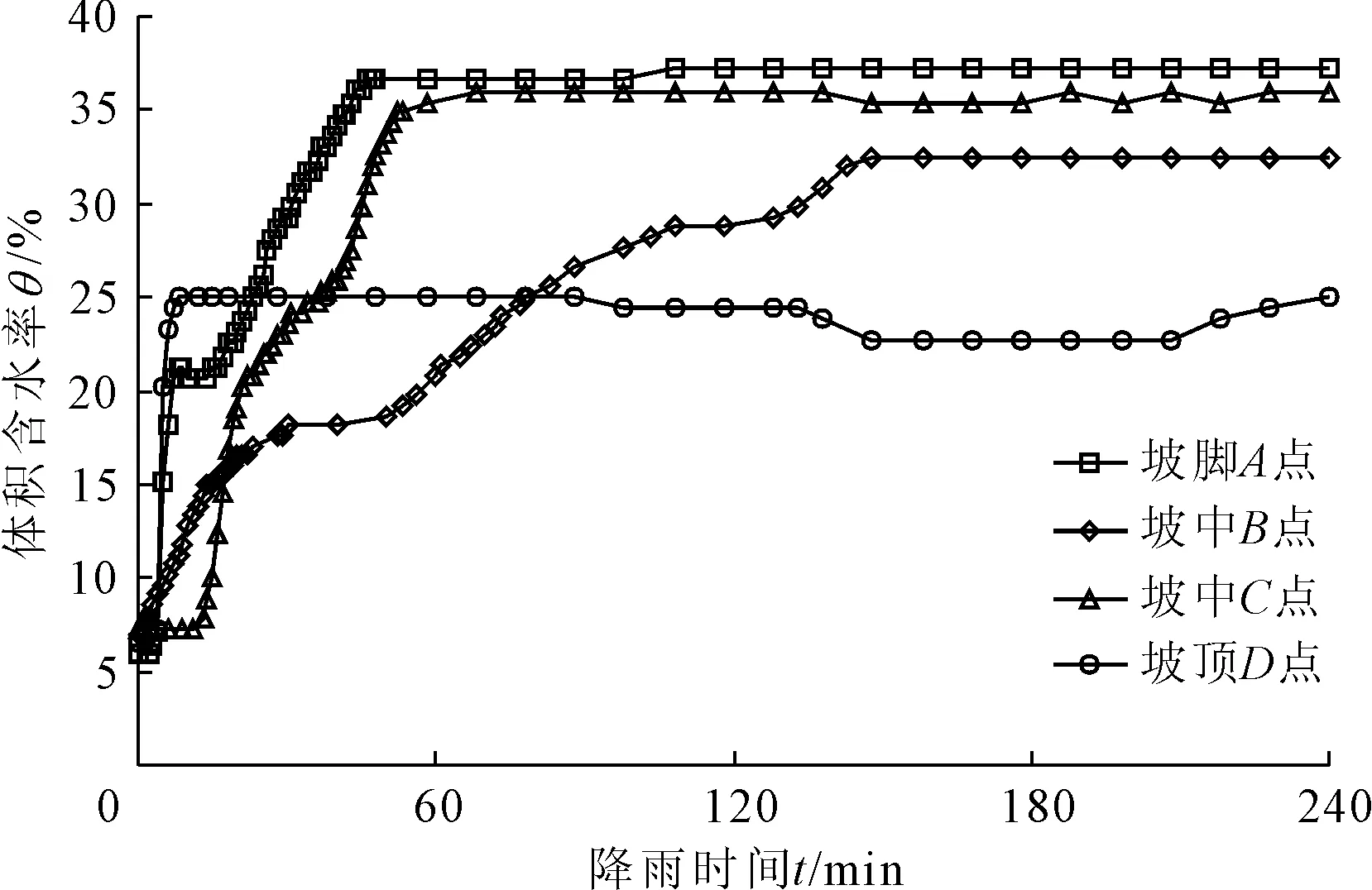
图3 体积含水率随降雨历时的变化曲线

初始平稳期内，由于雨水还未入渗到各测点，所以各测点的含水率基本保持不变，A、B、C、D四个测点的初始体积含水率大小依次为5.9%、6.9%、6.8%和6.6%。由于试验砂土渗透系数较大，降雨初期雨水入渗速率非常快，所以初始平稳期持续时间很短。

在上升期内，埋深均为10 cm的坡脚A点、坡中上部B点和坡顶D点三个测点，由于埋深较浅，因此传感器随降雨响应的时间都相对较短。降雨4 min后，各测点附近土体含水率开始增加；降雨7 min后，坡顶D点附近土体体积含水率率先达到峰值，大小为25.1%，但土体并未饱和；降雨46 min后，坡脚A点附近土体最早达到饱和状态，体积含水率大小为36.7%；降雨148 min后，坡中上部B点附近土体达到饱和状态，体积含水率大小为32.5%。埋深为20 cm的坡中下部C点，由于埋深较深，因此传感器随降雨响应的时间相对较长。降雨13 min后，雨水才入渗到此处，随后，该处附近土体含水率开始迅速增大；降雨58 min后，体积含水率达到峰值，大小为35.42%，土体达到饱和状态。

在最终稳定期内，顺坡向同一埋深为10 cm的三个测点，越靠近坡脚，含水率越大，例如坡脚A点、坡中上部B点、坡顶D点三个测点附近土体体积含水率大小依次为36.7%、32.5%和25.1%；在垂直坡面方向，边坡下部土体含水率大于上部土体，例如坡中下部C点(埋深20 cm)和上部B点(埋深10 cm)两个测点附近土体体积含水率大小依次为35.42%和32.5%。

(2) 边坡渐进变形破坏过程。边坡随降雨历时的破坏过程见图4。降雨7 min后，坡顶D点附近土体含水率率先达到峰值为25.1%，随后在降雨12 min后，坡顶后缘位置开始产生第一条裂缝；降雨31 min后，坡顶后缘位置开始产生第二条裂缝；降雨66 min后，坡顶已产生三条裂缝，该过程中坡土含水率一直保持稳定值为25.1%。此后，受降雨持续入渗的影响，裂缝逐渐向下发展。从图4(a)和图4(b)可以看出，降雨2 h后，距坡肩约10 cm位置处的第三条裂缝的长度已达到10 cm，坡土开始沿着第三条裂缝缓慢向下滑动。降雨4 h后，坡土沿滑动面缓慢向下滑动，发生渐进滑移变形破坏，如图4(c)和图4(d)所示。

进一步利用PIV系统分析降雨过程中边坡土体的位移场变化情况。由于PIV技术基于土体小变形假定，当降雨时间较长时，模型边坡土体位移较大，将会导致两张分析图片之间相关性较差，此时分析出的位移矢量图中乱点较多，误差很大，不能反映边坡土体的实际位移信息,因此利用PIV技术只分析了边坡在降雨120 min以内的坡土位移变形情况。

根据PIV系统处理得到的不同时刻边坡土体位移矢量数据发现，在降雨10 min时，坡土整体的变形较小，最大位移出现在坡脚处，为13.96 mm；随着降雨持续入渗，边坡上部土体的位移矢量开始增大，表明该处土体的变形增加，同时土体位移矢量的方向为顺坡面向下，表明坡土开始产生缓慢下滑；在降雨30 min时，边坡上部土体产生的位移变形较大，最大位移量为32.67 mm；在降雨60 min时，最大位移量增至53.19 mm，位移方式以顺坡向滑移为主；此后，随着降雨继续入渗，坡土不断下滑，在降雨120 min时，坡土最大位移达到86.22 mm。进一步将坡土中位移较大的点连成一条曲线，发现该曲线与图4(c)中试验边坡最终的滑动面形态基本相符。

在模型边坡中上部距离坡肩10 cm位置处取一个特征断面，利用PIV整理出该断面上各网格的土体位移信息，将该断面坡土顺坡向位移和滑移速度沿边坡土体深度的分布示于图5。

图4 边坡渐进变形破坏过程

土坡的滑移破坏一般可以从土体的剪应力增加或抗剪强度降低两个方面去分析其成因， 而降雨是影响二者的主要因素，降雨的入渗使得边坡的滑移呈现出渐进变形的特点。针对土坡的渐进式变形破坏，往往是先形成一个剪切区，然后从此区发展渐进地形成潜在的滑移面，在坡体渐进变形达到阈值时，坡体沿滑移面破坏，发生整体性滑动。据此将剪切区定义为剪切层，剪切层以上的整体滑动区定义为随动层，剪切层以下的稳定坡体定义为稳定层。从图5可以看出，降雨入渗初期，由于土体含水率变化较大，剪切层内坡土滑移速率较高；随着降雨持续入渗，由于坡土含水率不再发生明显变化，降雨入渗达到稳定状态(见图3)，剪切层内坡土滑移速率也逐渐趋于恒定。另外在图5(b)中，60 min曲线和其它曲线趋势不一致，这是因为在降雨60 min后，随着坡土含水率达到峰值，土体浸泡软化，抗剪强度迅速降低，导致降雨60 min对应的特征断面处坡土的顺坡向滑移速度显著提高，而后就逐渐趋于稳定值了。

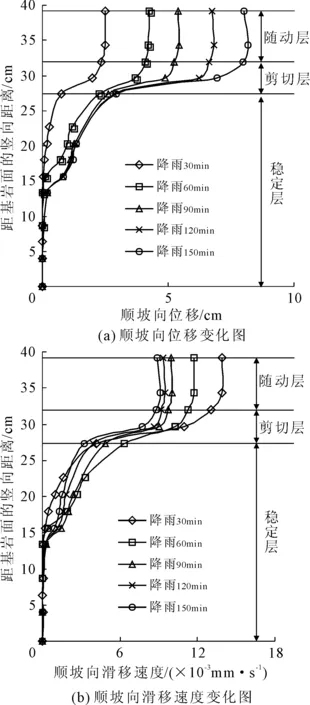
图5 模型边坡某特征断面顺坡向位移与滑移速度沿坡土深度分布曲线

根据位移和速度沿坡土深度方向的分布特征(见图5)，将位移和速度值逐渐增大且渐趋收敛于一常数值的土层区域，约32 cm～39 cm厚，近似认为是随动层[20]；将速度和位移值变化率最大的土层区域，约27 cm～32 cm厚，近似认为是剪切层；剪切层以下区域近似认为是稳定层(0～27 cm)。

2.2 坡脚浸泡试验结果与分析

坡脚不同时刻坡体形状变化如图6所示。从图6可以看出，由于试验模型尺寸较小，以及模型槽玻璃边壁对土的吸附作用，随着蓄水深度的增加，整个坡土没有出现整体性的滑动，而是坡脚出现了土体被不断软化和间歇性崩塌的现象。

图6 蓄水不同时刻坡脚破坏图

为了对比坡脚在水的浸泡作用下的变化情况，将不同时刻坡脚的崩岸顺序绘制到同一张图形中，如图7所示，图中虚线部分代表不同蓄水时刻的坡脚轮廓线。

从图7可以看出，在0～1 min、4 min～7 min和9 min～13 min时间段内，随着水位的增加，先对坡脚有较大的软化和崩解，之后分别在2 min、8 min和15 min时刻依次发生崩塌。由此可知，在长时间降雨浸泡作用下，岸坡坡脚由于软化和崩解效应，会出现坡脚土体被水流冲走的现象，进而引发整个坡体的滑动。

图7 坡脚形态随浸泡时间变化过程(单位：min)

3 结 论

通过对砂性土边坡进行坡面降雨和坡脚浸泡模型试验，可以得出以下结论：

(1) 降雨入渗过程中，坡土含水率的变化过程大致可以分为三个阶段：初始平稳期、上升期和最终稳定期。随着含水率的增大，边坡最终发生渐进滑移变形破坏。

(2) 根据模型试验土坡的渐进式变形破坏和沿坡土厚度的位移分布特征，可以将坡土由下至上大致分为三层：稳定层、剪切层和随动层。往往是先形成一个剪切区，在坡体渐进变形达到阈值时，坡体沿滑移面破坏，发生整体性滑动。剪切层以上的整体滑动区定义为随动层，剪切层以下的稳定坡体定义为稳定层。

(3) 随着坡脚水位的增加，岸坡坡脚由于软化和崩解效应，会最终引发坡脚崩岸，出现坡脚土体被水流冲走的现象，进而破坏边坡的整体稳定性。