神经网络-遗传复合算法在压水堆堆芯换料设计中的应用

韦子豪，王 端，王东东，潘翠杰

(1.中国原子能科学研究院，北京 102413；2.核工业研究生部，北京 102413)

压水堆核电厂投入运行后，在每个堆芯寿期末均要停堆换料。堆芯换料过程中，将产生大量的换料方案，而换料方案的选择直接关系到核电厂运行的安全性和经济性。一个优选的堆芯装载方案，可较好地展平堆芯功率分布、增加卸料燃耗深度、延长堆芯换料周期、提高燃料利用率，从而提高核电经济性和安全性。

堆芯优化装载方案的搜索是一项十分费时的工作，因为严格说来，压水堆堆芯换料方案设计是一个多变量、非线性的动态整数规划问题，现代数学理论已证明这类问题是NP-难问题[1-2]。典型3区装料的压水堆堆芯含193个燃料组件，即使在堆芯1/4对称布置且无可燃毒物的条件下，也有1043量级的堆芯换料方案，而且当堆芯燃料通道增加时，换料方案将会以指数甚至更多的形式增加[3]，这使得在众多的换料方案中快速找到1个全局最优的方案变得十分困难。

目前，国际上已围绕该问题利用各种优化方法开展了大量的研究，总的来说，主要分为确定性优化算法和随机优化算法，如线性规划、非线性规划、动态规划、直接搜索、专家系统等属于确定性优化算法[4-6]，而随机优化算法则主要包括模拟退火算法、遗传算法、粒子群算法、神经网络等[7-14]。但迄今为止，尚未有快速搜索出全局最优解的通用方法，其中有两个需要解决的主要问题。一是堆芯换料方案的优化建模问题，如何根据实际问题的需要建立合适的优化模型。优化模型主要包括目标函数、约束条件和决策变量三要素。在换料优化模型中，决策变量就是换料方案，另外两个要素的选择需仔细研究。二是优化算法的选择和计算效率问题。在换料优化模型中，目标函数与部分约束条件不能用堆芯排布方式的明确数学函数表示，它们的值仅能是已知堆芯排布方式的前提下，通过求解复杂的多群中子扩散方程和燃耗方程获得，这不仅导致依靠数学表达式的确定性优化算法使用受限，同时也是整个优化计算中最耗时的部分，使得快速、准确搜索出全局最优解成为一个非常困难的问题。

本文主要研究优化算法的选择和效率问题，自主设计一整套堆芯换料的智能优化程序，首先利用神经网络算法建立预测模型，再设计遗传算法快速搜索最优的堆芯燃料组件排布方式。通过神经网络与遗传算法结合的复合搜索算法改变传统依赖物理过程计算堆芯参数的做法所带来低效和复杂化的不利局面，快速高效地提供数量和质量兼备的优化换料方案，为智能化筛选换料方案提供新的可行方案。

1 数据处理

1.1 堆芯组件排布与样本取样

为维持反应堆可控链式核反应，堆芯装载多组燃料组件，这些组件按照一定的规律以阵列形式排布。如图1所示，压水堆堆芯上百个燃料组件的排列形状通常近似八边形阵列。

图1 堆芯燃料组件阵列Fig.1 Core fuel assembly matrix

燃料组件排布存在着一定的规律，以秦山二期压水堆为例，其排布方式呈1/8对称分布，因此仅需考虑其中1/8部分，如图2所示。共涉及4大类燃料组件E、F、G、H，除了新燃料组件H，同一燃耗次数的组件燃耗深度也存在差别，因此增加数字编号区分。由于组件仅能在固定区域进行调换，故将这1/8部分分为3个区域，以Ⅰ、Ⅱ、Ⅲ表示(标记为D12的组件是对称中心，固定不变，不将其纳入考虑范围之内)。

图2 1/8堆芯组件排布示意图Fig.2 Schematic diagram of 1/8 core fuel assembly arrangement

图2中共有16种不同燃耗深度的组件，为简便起见，若假设5个H组件的燃耗深度也不相同，则根据排列组合关系，可计算排布方式总数为6!×10!×4!=6.27×1010，其中，6!、10!、4!分别是Ⅰ、Ⅱ、Ⅲ区组件的排布方式总数。对于627亿种组合的排布方式，如果全部计算选择最优解，则会失去时效性与经济性。按如下3个步骤进行改进：1) 在所有排布方式中均匀抽样，选择10 000种组合作为样本；2) 建立高精度BP神经网络模型，根据样本数据进行训练，模拟堆芯排布-关键参数对应关系；3) 使用遗传算法快速搜索最优换料方案。

样本抽样过程为：从3个区所有排布方式中各随机抽取1种方式并进行组合，获得1个样本，重复抽样10 000次，即可获得10 000个一定程度上反映整个组合空间的样本。从这个过程可看到，作为样本数据仅提供输入输出的对应关系，不会涉及其中包含的复杂物理过程。

1.2 样本数据与输入输出向量处理

利用CASMO5程序计算每种排布方式下的堆芯关键参数，包括有效增殖因数(keff)、组件功率峰因子(Rad)和棒功率峰因子(FΔH)，这3种参数与堆芯排布方式一起，生成学习样本。

1) 样本总体特征

从样本数据读取其中独立的1/8排布信息作为输入，keff、Rad和FΔH作为标签，考察样本标签的分布规律。图3示出原始数据分布直方图。

2) 样本平衡处理

对于keff数据进行细致考察发现，其最大值为1.202 02，最小值为1.123 65，精度为0.000 01，意味着样本最多7 838个不同的数据，而实际是仅有4 304个，并且根据图3可知，值集中，一些值仅有1、2个。对样本进行如下平衡处理：(1) 该值在样本中仅有1个，进入训练集；(2) 该值在样本中存在N个，进入训练集的概率为(1/N)-1/2。如果未进入训练集，则进入测试集。

最终获得的keff数据训练集和测试集样本分布如图4所示。可看出，训练样本分布更均匀，方差更大。

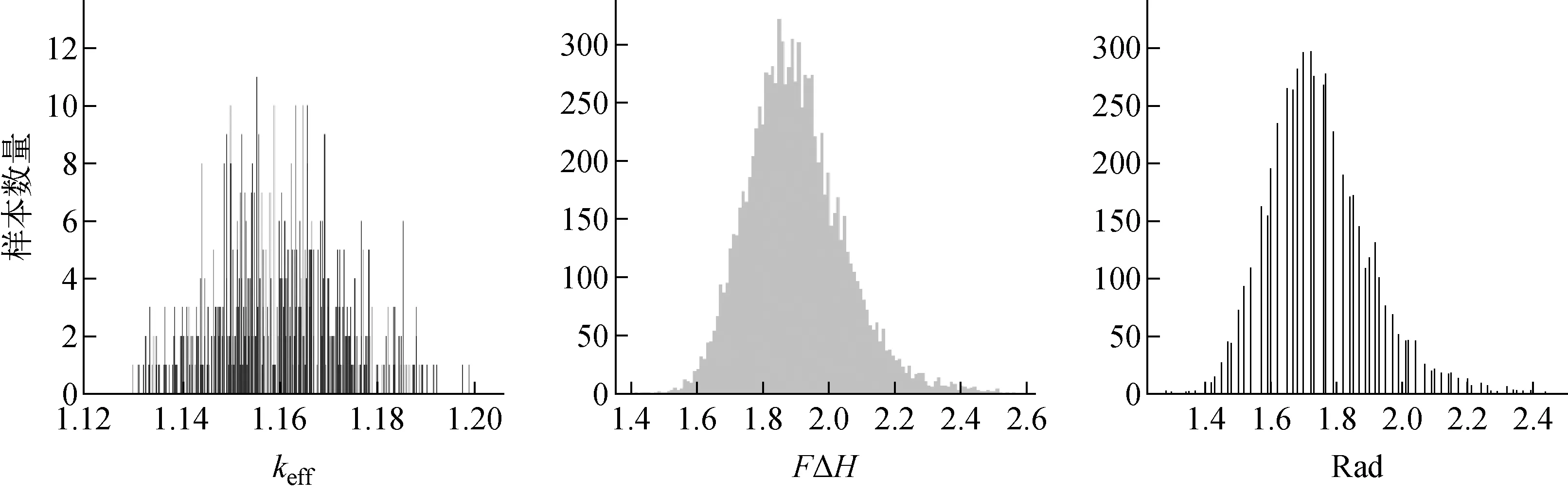
图3 原始数据分布直方图Fig.3 Raw data distribution histogram

图4 处理后的样本分布直方图Fig.4 Processed data distribution histogram

同样对Rad、FΔH数据进行平衡处理，但由于它们更加集中，为不破坏原始数据的分布，采用简化的平衡样本的方式：从标签在均值±1左右的样本中选取1 000组作为测试集，其余作为训练集。

3) 输入向量选择

在文献[15]中，将E、F、G、H 4种组件表示-1到1的等差数列，即-1、-1/3、1/3、1。这种方法过于简化，对预测精度有较大影响，因此本文使用4位二进制数表示16种不同燃耗深度的组件，对应情况列于表1。这样，每个包含20个组件的排布方式x=(1，1，1，1，0，0，0，0，…，1，0，1，1，1，0，0，1)T均是1个80维的输入向量。

表1 组件与编码对应关系Table 1 Correspondence between component and coding

4) 输出向量的处理

每个样本标签为3个关键参数，为提高精度，采用3套不同网络训练，分别设置输出层为1个节点，输出向量长度为1。

2 建立预测模型

理论研究证明，多层前馈网络即能以任意精度逼近任意复杂度的连续函数(万能逼近定理)[16]。但要使神经网络能较精准地拟合1个复杂函数，设置其网络结构如隐藏层数、节点数量等，并进行有效训练是比较困难的，目前尚未有通用办法，仅能根据经验反复尝试。为更快速获得较好的模型，对训练的模型提出评价指标。本文主要使用的误差是绝对误差：

(1)

式中，ypredict、ylabel分别为预测值、真实值。

2.1 模型评价指标

1) 敏感性与适应性分析

利用神经网络算法解决问题时，要求输入输出数据之间强的相关性，一般需进行特征分析和选择，本问题中输入数据为燃料组件的类型与排布规律，对输出数据有决定性的影响，因此是强相关的特征，比较可靠。输出数据的3个堆芯关键参数在精度上不同，对噪音干扰的敏感性也不同。keff精度要求高，因此模型预测产生的误差也同样要求严苛，而对于其余两个参数数据则可降低标准。本文认为，模型对keff预测的平均误差不高于0.05，对FΔH预测的平均误差不高于0.5，而对Rad预测的平均误差不高于0.5即是可靠的。

另外，对于与训练样本相似或相邻的数据，拟合结果是相对精确的，但对于整个解空间的极值(这些值在训练样本中没有或很少)，拟合的结果会差一些，而且受模型优劣的影响较大。

2) 评价指标

用以下6个指标评价模型的优劣。(1) 训练误差(MAEtrain)与测试误差(MAEtest)，即10 000组样本在训练模型中最终对应的训练误差和测试误差，它们能反映训练情况，之间的差距还能反映拟合情况，即过拟合或欠拟合。(2) 模型最大误差(MAEmax)，即模型在所有样本中的最大绝对误差。(3) 模型平均误差(MAEavg)，即模型在所有样本中产生的平均误差。(4) 验证数据(td)，即一些未参与训练的关键数据，如CASMO5计算出的当前堆芯最优数据为：keff=1.127 21，Rad=1.20，FΔH=1.388。另外一些表征样本边界的数据，即样本中标签极值，如keff样本最大值为1.202 02，Rad样本最小值为1.28，即为样本边界数据(bd)。(5) 超阈值误差数量(ot)，即超过一定绝对误差阈值(如0.1)的样本数量。(6) 模型预测极限(lp)，即模型能预测到的整个解空间中最值。由于实际全局最优解难以确认，以遗传算法搜索到的最值作为替代。

泛化误差为模型在一些未知数据上预测的误差，是模型优劣最核心的评价标准。但需预测的数据仅有输入已知，标签未知，无法计算误差。因此，1个模型优劣的评判也是神经网络算法所面临的现实问题之一。除了通常使用的训练误差和测试误差之外，实验发现以上几个指标也可从不同方位给出一个模型的训练情况和泛化能力。

因此，在使用遗传算法搜索最优结构时，使用的适应度应综合考虑这些指标，为此，可拟定适应度函数如下：

(2)

式中：MAEtrain为训练误差；MAEtest为测试误差；MAEmax为样本总体的最大误差；MAEavg为样本总体的平均误差；|xp1-bd|为对边界值的误差；|xp2-td|为对验证数据的误差；ot为误差超过0.05的样本数量；lp为模型预测的极限值；δi(i=1,2,…,8)为各项系数，代表各项的影响权重。

2.2 网络模型

对于keff数据，由于精度较高，基于奥卡姆剃刀原则，单隐层BP神经网络即可训练出一个比较满意的模型。但Rad和FΔH的样本精度低、方差小，为更好学习到数据特征，使用深度神经网络(DNN)模型，其拓扑结构如图5所示。

图5 包含3个隐藏层的BP神经网络结构示意图Fig.5 Schematic diagram of BP neural network structure with three hidden layers

经实验确定的keff、Rad和FΔH预测模型的结构列于表2。

图6为keff、Rad和FΔH训练过程误差和学习率的变化，使用dropout减少过拟合，使用持续减小的学习率使模型尽可能向全局最优收敛，可见训练的收敛情况表现比较理想，得到的最佳模型是较为可靠的，其中模型的评价指标列于表3。模型对样本的平均误差均小于0.05，与敏感性分析中预期的值相符合，对边界值和特殊的验证数据的预测误差也很小，说明模型拥有一定的泛化能力。

表2 3个预测模型网络结构信息Table 2 Structure information of three predictive models

注：隐藏层后括号内为dropout节点重置率，即不进行参数调整的神经元比例

图6 keff(a)、Rad(b)与FΔH(c)模型训练中收敛情况数据图Fig.6 Figures of convergence in model training in keff (a), Rad (b) and FΔH (c) data

表3 模型的评价指标
Table 3 Evaluation index of models

关键参数MAEtrainMAEtestMAEmaxMAEavgbdtdotlpkeff0.001 10.001 10.003 20.001 11.201 02(1.202 02)1.128 13(1.127 21)01.206 89Rad0.0440.0430.110.0441.3(1.28)1.23(1.20)301.143FΔH0.0490.0460.120.0481.403(1.411)1.422(1.388)141.321 7

注：括号内为对应样本的标签值

3 遗传-神经网络复合搜索算法设计

3.1 适应度与目标函数

1) 优化目标[17-18]

本文数据针对的是秦山二期平衡循环(换料周期12月)，堆内无可燃毒物，因此以参数keff、Rad和FΔH作为优化目标。具体目标是，在可行域范围内，搜索使堆芯参数最优的组件排布方式，使keff最大化，Rad和FΔH最小化。以f(x)表示目标函数，则表达式为：

f(x)=∂kefffkeff(x)+∂RadfRad(x)+

∂FΔHfFΔH(x)+δ

(3)

式中：δ为1个常量，用以保证f(x)为正值；∂keff、∂Rad、∂FΔH为3个堆芯参数的适应度所占的权重。以f(x)的最大化为目标，其约束条件为∂keff≥0，∂Rad≤0，∂FΔH≤0。

权重的正负决定对应参数的优化方向，权重绝对值的大小决定参数的重要程度。

2) 适应度选择与尺度变换

单纯以目标函数为适应度会发生早熟和停滞现象，因此引入简单的适应度尺度变换。最终确定适应度计算公式为：

fitness=f4(x)=(2fkeff(x)-

3fRad(x)-5fFΔH(x)+24)4

(4)

3.2 遗传算子设计

遗传算法认为生物进化的本质是染色体的选择、交配与突变。借助该思想，遗传算法主要包含的算子为选择、交叉和变异算子。而在第1.1节已指出，将不同燃耗次数组件以E、F、G和H表示，不同燃耗深度的组件则使用字母与数字结合标记，因此1个20个组件的排布方式可使用按照一定顺序连接形成1个基因序列，即对应遗传算法的编码，如“H02F34F26F35-G02E34H01H08G10G04F32H05E07G19F07-H04F01E36F29G27”。

1) 选择算子

使用轮盘赌选择与最优保存策略结合的选择算子。轮盘赌选择使用随机采样方法，即蒙特卡罗方法，从N个个体中有放回的随机抽取N次，作为下一算子的输入，每个个体被抽取的概率由其适应度决定，其公式为：

(5)

式中：fi为第i个个体经过尺度变换后的适应度；Pi为其被选中的概率。

进行轮盘赌选择前，将当前适应度最高的个体保存，作为新一代种群的1个个体，保证适应度最高的个体总参与遗传、变异，这就是最优保留策略。

2) 交叉算子

使用保留基因片段的方法进行交叉，即在子代中保留父代被选择保留的基因段。在父代(1)中选择保留的基因段，在子代(1’)中将保留并保持位置不变，并将父代(2)中与这些保留基因相同的基因去掉，然后将剩下的基因按照一定的顺序(如原来的顺序)填充到子代(1’)余下的位置形成新的子代(1’)，同理可获得子代(2’)。与一般的交叉算子不同，为使生成的子代依然满足约束条件，即包含在解空间中，要在保留1个父代的基因后，对另一个父代基因进行筛选。

每次保存的基因均应保持一定的长度以保持父代基因的特征，不同的长度意味着信息的不同的保留率，可在实验中检验不同信息保留率对搜索结果的影响。本文对3个区的基因设置不同的交叉概率参数，以向量Pc=(pc1,pc2,pc3)T表示，其中元素分别表示Ⅰ、Ⅱ、Ⅲ区的交叉概率。在迭代进行过程中，根据一定规则改变交叉概率，有利于算法平衡全局搜索能力与搜索时间的关系，本文在前期以较高的概率进行交叉，而后期则逐步降低交叉的发生概率。当发生交叉时，使用保留上一代1/2的基因信息。

3) 变异算子

设置变异概率向量Pm=(pm1,pm2,pm3)T，分别对染色体的3个区间进行变异操作，即随机选择两个不同位置，交换该位置上的1对基因顺序从而生成新的1代。变异前后个别组件发生调换而产生变异，与交叉类似，变异随着时间的进行，其概率有所变动以改变其局部搜索的能力，在迭代后期可适当增加这一能力以尽可能在局部上达到最优。

3.3 流程图

遗传算法的流程如图7所示。

对于图7，有如下两点说明。1) 通过抽样数据获取学习数据集，通过数据处理生成训练集和测试集，使用训练集对预测模型进行训练，当在测试集的绝对平均误差小于1个预设的预定值时获得最终的预测模型。2) 遗传算法通过随机数初始化一定规模的种群，获得输入Xm，将Xm作为预测模型的输入获得预测值，从而根据适应度计算公式计算出适应度。种群根据适应度进行3个算子的变换，并记录过程中最优的解。当迭代次数或最优解满足停止条件时，停止迭代，输出结果。

4 优选压水堆堆芯换料方案

设置原始杂交概率Pc=(0.6,0.9,0.5)T，变异概率Pm=(0.05,0.1,0.05)T，种群数量N=100～400，迭代次数为200～1 000，进行多次搜索，搜索时间为5～10 min。其中1个结果的情况如图8所示。表4列出优选的换料方案对比。图9为其中1个最优解(预测值1)对应的排布方式，图9a为基因序列按照从右到左、从上到下的顺序填充的1/8堆芯，图9b为基因序列对应的完整堆芯。

图8a指出遗传算法在迭代300次左右、耗时数min内可搜索到最优解，图8b指出适应度限制了对keff的最大化搜索，因此如果需要可改变适应度函数以获得更高的keff。表4列出本文提供的集中优选堆芯方案和对应的参数的预测值，在误差范围内与目标值相当或更好。

图7 神经网络-遗传复合算法的总流程图Fig.7 General flowchart of neural network-genetic composite algorithm

图8 复合算法的适应度变化曲线Fig.8 Fitness curve of composite algorithm

表4 优选的换料方案对比
Table 4 Comparison of preferred refueling scheme

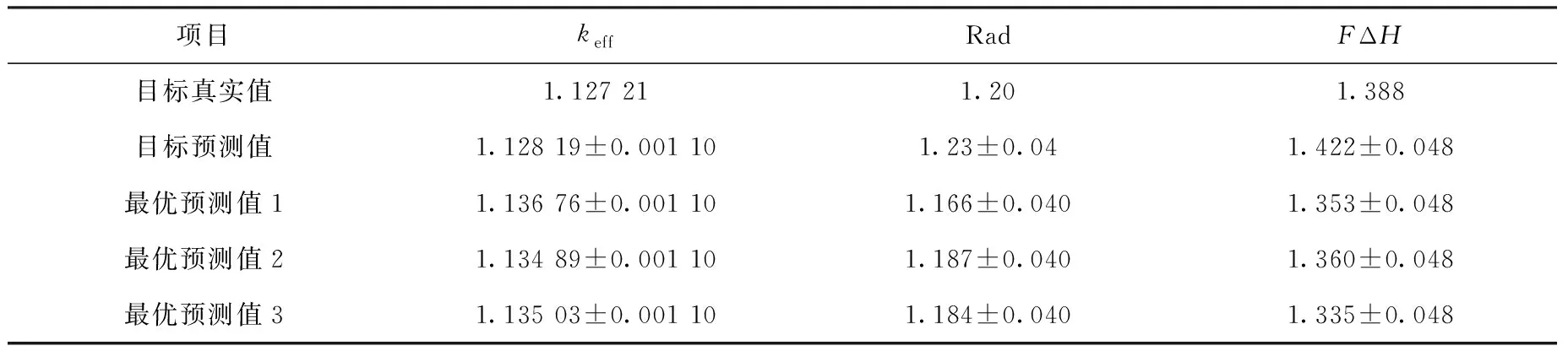
项目keffRadFΔH目标真实值1.127 211.201.388目标预测值1.128 19±0.001 101.23±0.041.422±0.048最优预测值11.136 76±0.001 101.166±0.0401.353±0.048最优预测值21.134 89±0.001 101.187±0.0401.360±0.048最优预测值31.135 03±0.001 101.184±0.0401.335±0.048

图9 其中1个最优解(预测值1)对应的排布方式Fig.9 One of optimal solutions (prediction 1) corresponding arrangement

实验表明，采用神经网络-遗传复合算法可预测不同堆芯排布方式下的关键参数，并利用生物的遗传进化机制，在大量排布方式下快速搜索更优的堆芯排布方式。1个训练很好的神经网络模型对超出样本数据所在区间外的预测精度会下降，导致搜索的范围不能太大。解决这一问题的方法是，根据已获得的最优结果再次训练网络、再次搜索，不断迭代，向更优的结果靠近，直到搜索到全局最优解，这是下一步的工作。

5 结论

建立自适应神经网络提供堆芯参数，再结合改进的遗传算法进行堆芯换料方案的筛选，快速、准确选择较优的堆芯换料方案。其结果可推广至任意堆芯堆型、任意关键参数预测，并且可很容易地优化修改目标函数，筛选符合实际需要的换料方案。该方法不需特定领域的专业知识，仅要有足够多的数据，即可实现精度较高的快速预测，但需对模型作进一步的敏感性分析和适应性研究。