基于出口流水数据的高速公路节假日日OD交通量分布预测
2020-05-29
(1.广东省交通集团有限公司, 广东广州 510623;2.华南理工大学土木与交通学院, 广东广州 510641)
0 引言
高速公路在交通系统中承担着十分重要的功能,是交通网络系统中不可或缺的组成部分,同时也与国家、地区的经济发展水平有着密切的联系,伴随着高速公路基础设施建设逐步完善、高速公路联网收费系统逐步健全,人们日益希望用科学的手段提高高速公路的运营管理水平,尤其是提高高速公路交通诱导的智能化水平。高速公路OD(起讫点)交通量数据是获取各区域间以高速公路为运输方式的出行需求的重要基础数据,因此在掌握高速公路历史流量数据的基础上对未来OD交通量进行准确的预测,是我国高速公路交通步入智能化的重要基础条件。
1 研究现状
传统的OD交通量预测方法为“四阶段法”,此法在实际中被广泛认可并大量使用于工程中,四阶段的各个阶段均有成熟的理论和模型,如Fratar法[1]、Furness法[2]、最大熵法[3-4]等。张秋美等[5]提出了综合使用多种方法进行四阶段预测的高速公路交通量预测方案,所使用的方法包括增长率法、福莱特法、重力模型法。丁志坤等[6]提出基于改进“四阶段法”的高速公路交通量预测方案,并应用于杭州绕城高速公路交通量预测中。
然而“四阶段法”调查资料获取、整理以及预测工作过程都较为繁杂,具有明显的弊端。对此有学者提出根据路段检测流量反推OD矩阵的思路,现已提出的反推算法有最大熵法[7]、极大似然估计法[8]、贝叶斯法[9-11]、卡尔曼滤波[12]等。
与交通量预测相关的研究已有不少,由于交通与社会、经济、土地的密切关系,大量的研究通过分析相关统计数据与交通领域数据的关系实现对未来交通数据的预测,XU等[13]提出基于线性回归模型的地级市高速公路客运量预测方法、AHN等[14]提出使用支持向量机和贝叶斯分类器预测高速公路交通流的方法。针对先验数据难以完整获取的情况,宁建根等[15]立足于收费站的历年统计数据,提出一种模糊优化灰色预测法,用于高速公路OD矩阵估算,该法仅基于所需预测数据自身的变化规律,因此预测工作量少、可操作性强。
受益于高速公路联网收费系统,现阶段我们能够获取可靠完备车辆进出收费站数据,进而通过统计得到高速公路历史OD交通量数据,而此数据在传统方法中往往难以直接获得。借助精准的历史数据,本文提出基于高速公路出口流水数据的节假日高速公路日OD交通量分布预测方法,首先使用综合考虑多因素的多元线性回归预测模型对节假日范围内总OD需求进行预测,而后基于历史各日占总量的比例将所预测的总量分配至各日。下文将以广东省西片区高速公路网2018年节前春运日OD交通量分布预测工作为例,阐述所提出预测方法。
2 方法介绍
2.1 节假日的选取
本算例选取节前春运作为预测节假日。随着车辆保有量逐步提高,越来越多人选择在节假日自驾车出游或是探亲访友,这使得每到重大节假日,都会有大量的出行需求涌入高速公路。而春节作为中国文化中最重要的节日,在外工作者的返乡需求极大。加之春运期间实行高速公路免收小型客车通行费政策,价格杠杆下进一步增加了选择高速公路返乡者的数量。此外,根据江文平[16]关于上海市春运客流出行特征的研究,春运期间由于铁路运能紧张,以长途汽车为交通方式的比重上升。综上可得春运期间产生的出行需求为各大节假日中最多、对高速公路造成压力最大,因此对春运期间的高速公路日OD交通量分布进行预测,具有更为重要的意义。
2.2 数据源介绍
数据基础为珠三角部分地市及粤西所有地市的共447个收费站的收费出口流水数据,该数据记录了经MTC、ETC通道进出路网的所有车辆的入口收费站信息、出口收费站信息、驶出日期及时间等信息,数据时间范围为2015~2017年除夕前-20 d至除夕后8 d(以除夕日为0的相对天数:除夕前为负值,除夕后为正值)。高速公路收费出口流水数据作为高速公路收费的唯一依据,准确性是极高的,因此借助高速公路收费流水数据,我们可以直接且精确地获取历史OD交通量矩阵。并使用历史OD交通量、结合宏观经济数据对未来OD交通量进行预测。
2.3 交通小区划分
根据各收费站处于高速公路路网中的位置,划分出23个交通小区,划分情况如图1所示,各小区的行政区域范围见表1,从图1可见,所有交通小区区内均覆盖有在用收费站,这保证了小区之间有高速连通。所划分的交通小区分为三大类,第一类为珠三角环线高速内的收费站,编号为0号交通小区,此区域是春运节前返乡出行最大的出行产生区域,以及春运节后回程出行最大的出行吸引区域。第二类为粤西各地市,我们结合其所属行政区域以及其所处于路网中区位来进行划分。第三类为可从粤西高速公路路网进入广西的地市,由于所有的跨省车辆均需在省界主线收费站交取广东省路网通行费后方可出省,因此我们将对应的省界站划入广西地市分区,节前春运大量人群返乡至广西、会产生大量的出省需求,我们认为从这些省界站驶出的车辆会以对应的广西地市为目的地。
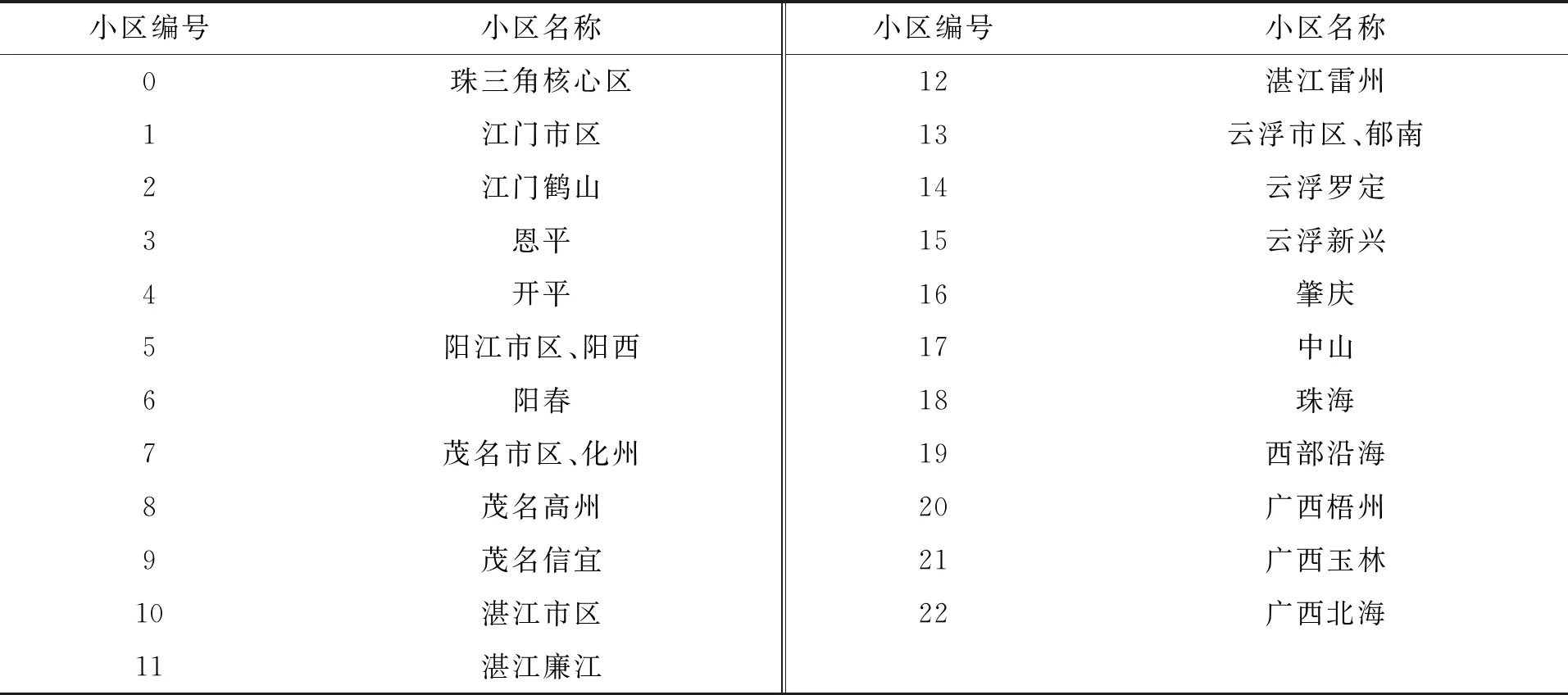
表1 交通小区划分情况Tab.1 Information of each zone
随着车辆保有量逐步提高,越来越多人选择在节假日自驾车出游或是探亲访友,这使得每到重大节假日,都会有大量的出行需求涌入高速公路,春节作为中国文化中最重要的节日,在外工作者的返乡需求极大,加之春运期间实行高速公路免费政策,价格杠杆下进一步增加了选择高速公路返乡者的数量,综上可得节前春运期间产生的出行需求为最多、最集中。高速公路的年出行高峰出现在春运期间,因此预测得到春运时段内的高峰小时即可作为年高峰小时预测值。
2.4 春运节前返乡OD交通量特征分析
首先通过数据库查询统计获取2015~2017年从珠三角核心区(0号交通小区)去往粤西各地市及广西各地市的历史日OD交通量数据,具体方法是统计出口流水中从各起点交通小区进入、并在各终点交通小区驶出的流水数量,即统计从起点交通小区所包含收费站出发、并在终点交通小区所包含收费站驶出的日车辆数。
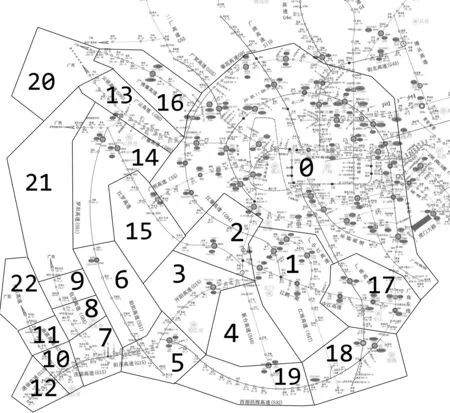
图1 粤西高速公路收费站分区图
通过分析历年春运期间日OD交通量分布,可以粗略了解其交通量随时间的变化规律,以从珠三角核心区(0区)去往粤西阳江市区(5区)、茂名市区(7区)、湛江市区(10区)、云浮市区(13区)四市市区四个OD的过去3 a日OD交通量分布数据为例(见图2,以除夕日为0的相对天数:负值为除夕前,正值为除夕后。),可见每年的除夕前两周,收费站出口流量均一致出现明显的上升,此后持续增长、并在除夕前5 d至2 d达到峰值,在除夕当天降至极低水平,此后保持低位,至大年初六左右开始明显回升。结合我们对春运节前返乡行为已有的认知,上述交通量分布特征是合理的,除夕前两周左右开始有人启程返乡,此后随着除夕越发临近,返乡需求越发迫切、返乡的流量逐日递增,当然绝大多数的人不会选择除夕前一天匆忙赶到家乡、而是预留数天在家乡置办年货、大扫除、准备年夜饭等,因此返乡需求的峰值出现在除夕前-2~-5 d,至除夕开始节前春运结束,此后基本处于全民停工状态,一直到大年初六开始逐步恢复生产。
根据对历史数据的分析结果,我们将节前春运时段定为除夕前-14 d至除夕当日。由于原始出口流水数据获取渠道的限制,用于预测的历史数据覆盖年份为2015年至2017年。
相比于受突发因素(如天气、路况)影响较大的日交通量和小时交通量,重大节假日时段的OD交通总量具有更强的规律性和趋势性,因此我们首先对重大节日时段内的总OD交通量进行预测。节前春运时段,高速公路出行者的出行目的绝大多数为返乡、探亲,由于文化的因素,春运是一项在外工作人口参与比例极高的行为,因此可推断春运节前返乡交通总量与终点小区的人口关系密切。除了人口的因素,终点小区的汽车保有量较明显地影响着选择自驾小汽车返乡的潜在人数,终点小区的经济发展水平则可能间接影响着自驾回乡的人数。此外,从起点小区到终点小区的高速公路最短距离影响着人们选择自驾车返乡的意愿。影响自驾返乡意愿的因素还有该小区的高速公路网可达性,而可达性可以通过地区的高速公路网里程密度、地区的收费站密度衡量。
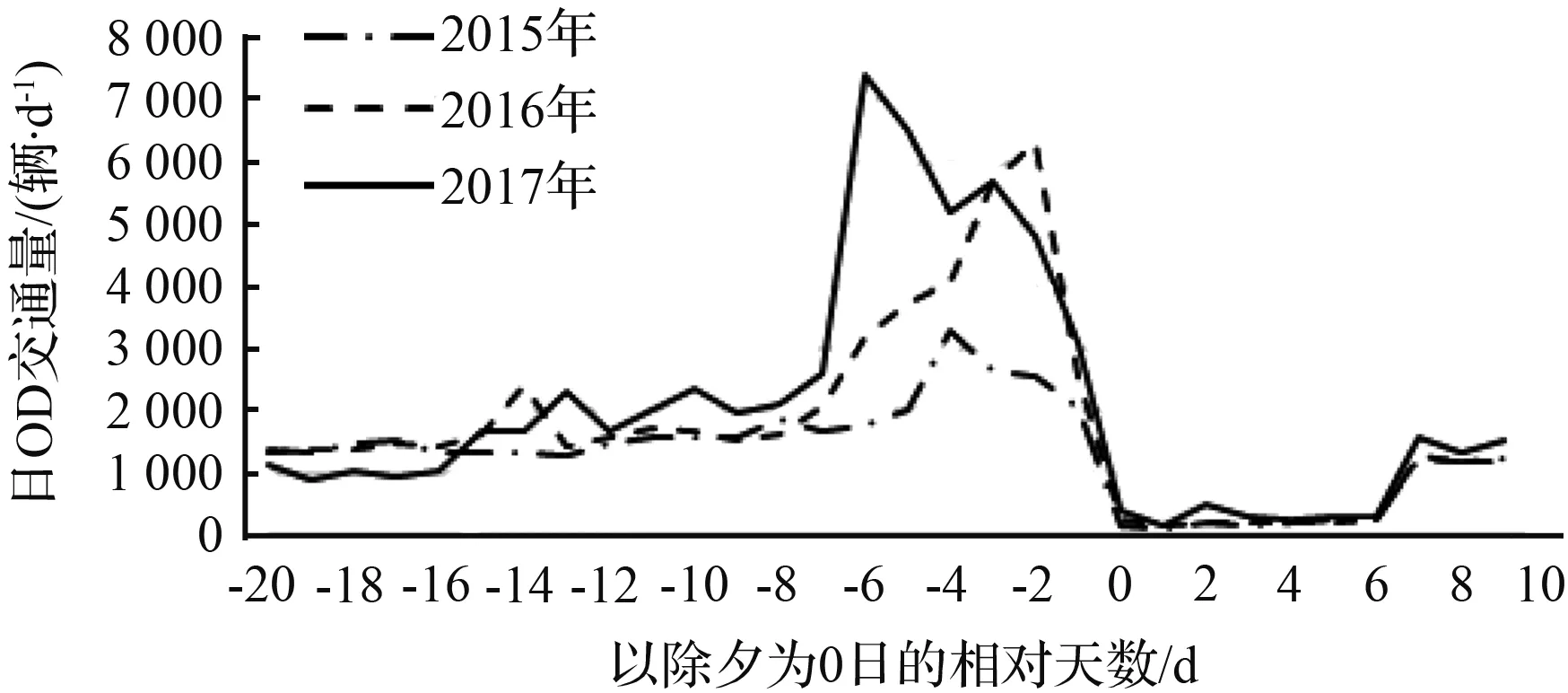
(a) 0区至5区历年节前春运日OD交通量分布
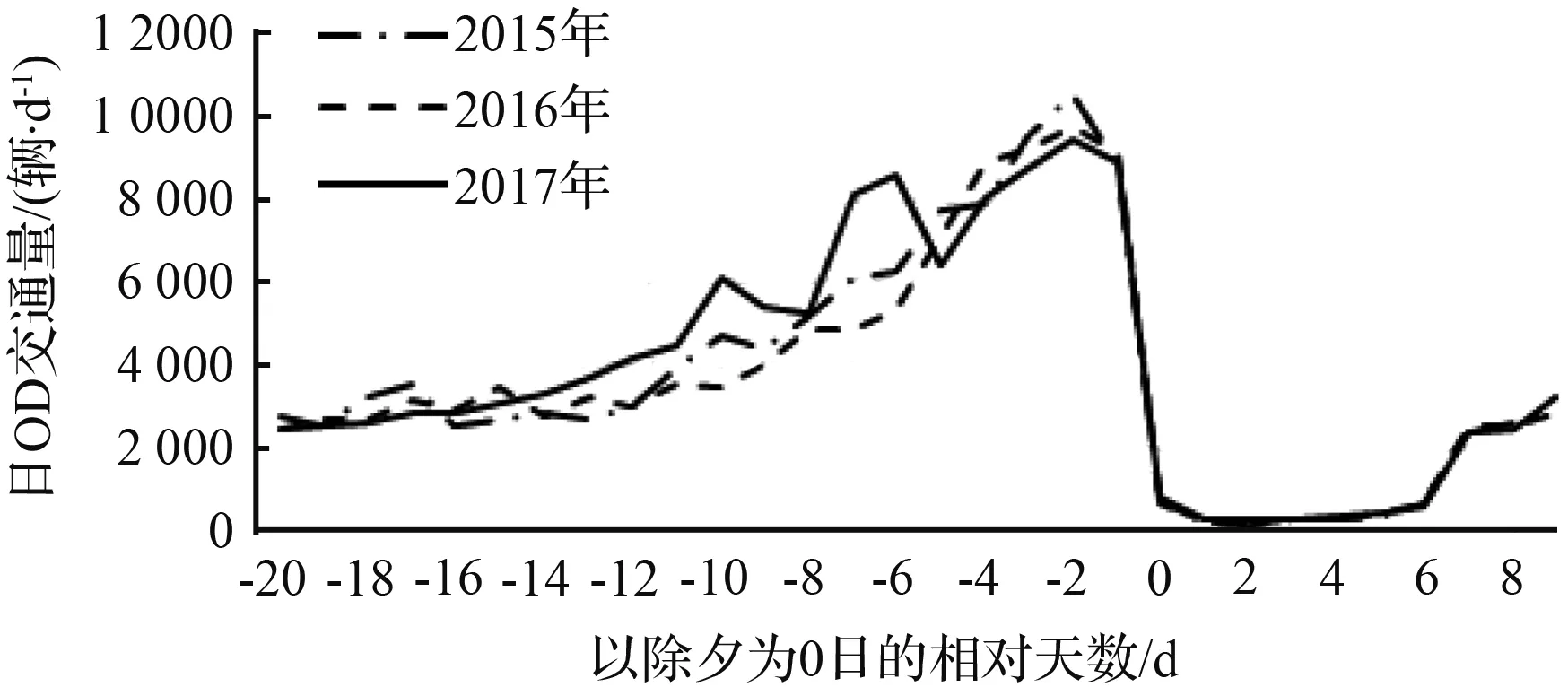
(b) 0区至7区历年节前春运日OD交通量分布
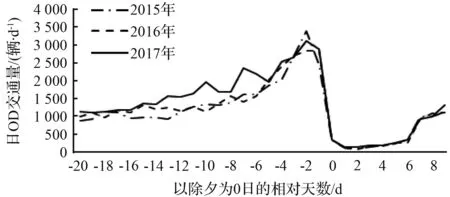
(c) 0区至10区历年节前春运日OD交通量分布
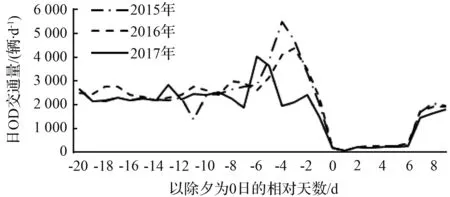
(d) 0区至13区历年节前春运日OD交通量分布
图2 珠三角核心区至粤西各交通小区历年节前春运日OD交通量分布
Fig.2 Daily traffic volume distribution of ODs from Pearl River Delta corearea to urban area of perfecture-level cities of west Guangdong
基于上述的已有知识,考虑到春节前从珠三角核心区返乡的需求与多个因素有着紧密联系,我们采用多元线性回归的方法来对从珠三角核心区去往粤西及广西各交通小区的节前春运总OD交通量进行预测。
2.5 基于多元线性回归的节假日期间总OD交通量预测
多元线性回归是一种常用的数理统计方法,当一个变量与明显受到多个变量影响、自变量和因变量之间的线性相关关系真实存在、且自变量具有完整的统计数据时,使用该模型可以达到优良的解释能力和预测效果。
我们取终点小区的汽车保有量、终点小区的地区生产总值、终点小区区内高速公路里程密度、终点小区区内高速公路收费站密度、终点小区户籍人口、从珠三角核心区去往终点小区的最短路距离这6个变量作为自变量,并分别定义为x1,x2,x3,x4,x5。
需要说明的是,高速公路里程密度指区域境内高速公路总里程与区域总面积的比值,高速公路收费站密度指区域境内高速公路收费站数量与区域总面积的比值
历史数据覆盖年份为2015、2016、2017年,因此多元线性回归表达式为:
(1)
写成矩阵形式为:Y=Xβ,
其中:
Y为历年除夕前-14 d至除夕当天从珠三角核心区去往粤西及广西各交通小区的总OD交通流量,β是多元线性回归方程的待定系数矩阵。
2.6 将总预测量分配至各日中
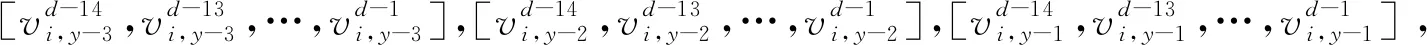
(2)
即根据历年各日占总量比例的平均值,将所预测的总量值分配到各日中去,从而得到最终的日交通量预测值。
我们以从珠三角核心区去往湛江—雷州市分区(小区编号为12)OD为算例,首先算得历年节前两周从珠三角核心区去往湛江雷州分区的OD交通量总量,使用前文所述多元线性回归方法预测得到的2018年节前两周OD交通量为38 191 辆,此后计算历年节前两周各日OD交通量占该年节前两周OD交通量的比例,此后计算过去3 a同日占比平均值,作为预测年2018年该日占比预测值,最后将各日占比乘上2018年节前两周总量预测值,即得到各日OD交通量预测值,计算过程见表2。
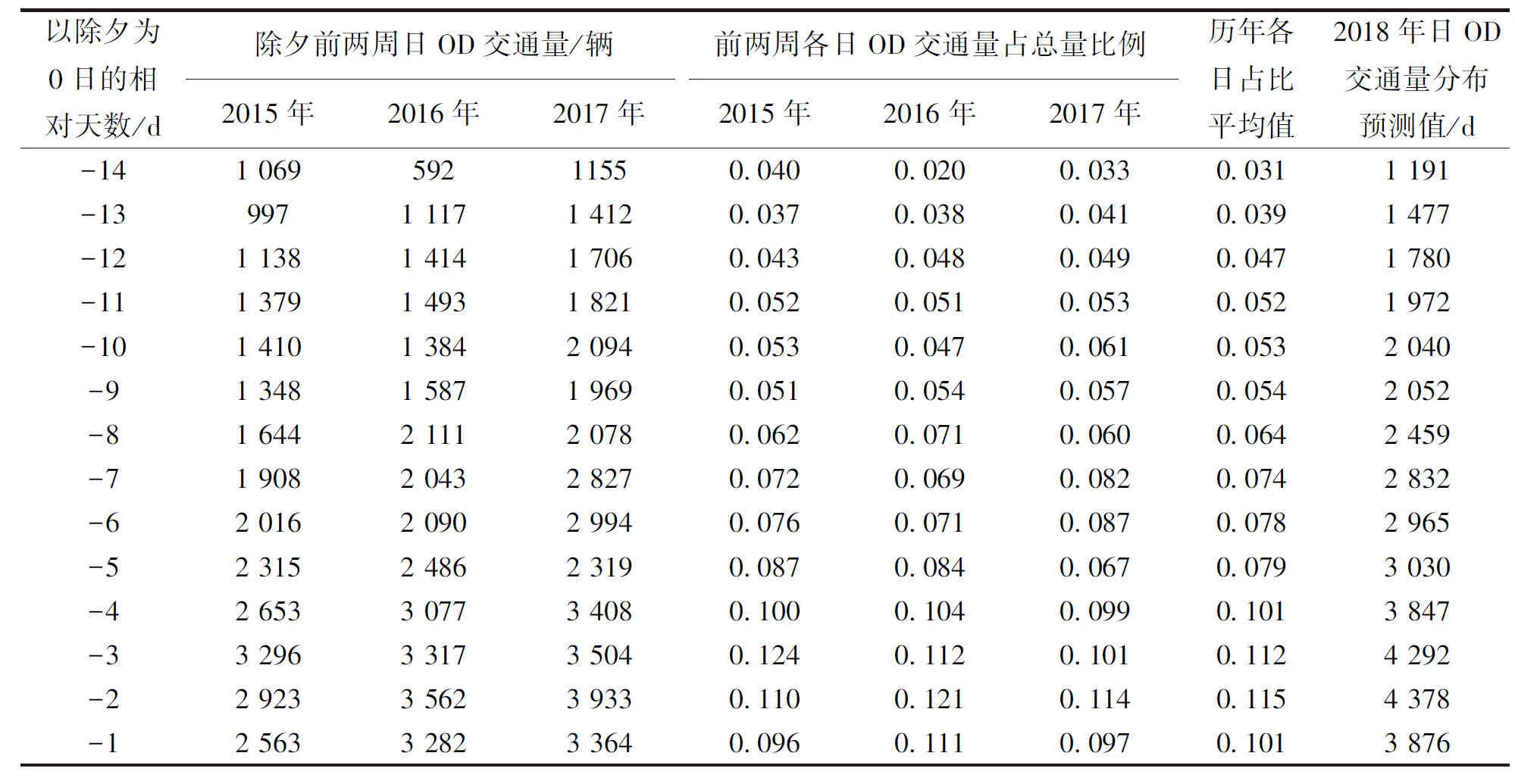
表2 将总OD预测量分配至各日算例Tab.2 Examples of assigning total OD predition volume to each day
2.7 预测准确性检验
我们使用均方根误差(εRMSE)和平均绝对百分比误差(εMAPE)作为衡量预测准确性的误差函数,计算公式如下:
(3)
(4)
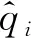
对大需求OD的预测是更有意义的,根据已有知识的判断以及对历史数据的分析,从珠三角核心区出发去往粤西各市市区、以及从珠三角核心区出发过境去往广西方向的需求是最大的,因此选取从珠三角核心区(0交通小区)出发,去往粤西各地市市区以及广西各方向的OD,对这些地市市区以及广西各方向的OD,对这些OD的节前春运日交通量分布预测准确性进行评价。这些目的交通小区包括阳江市区(5交通小区)、茂名市区(7交通小区)、湛江市区(10交通小区)、广西梧州方向(20交通小区)、广西玉林方向(21交通小区)、广西北海方向(22交通小区)。
图3为这些重要起讫小区的预测结果与真实结果的比较图,从该图可见,使用所提出方法预测得出的各起讫小区日OD交通量分布曲线与实际曲线走势是大致吻合的。表3所示为各个OD的预测结果平均绝对百分比误差,以MAPE的标准,除了0区到22区外的其余起讫小区之平均绝对百分比误差均在15 %左右的水平。这样的MAPE意味着日OD交通量规模约为1 000 辆/日的情况下,节前春运-14 d的日平均误差为150 辆/d;规模约为 5 000 辆/d的情况下,日平均误差约为750 辆/d;规模约为10 000 辆/d的情况下,日平均误差约为1 500 辆/d。这样的误差规模对于日OD交通量预测而言,是较为理想的。
(a) 0区至5区
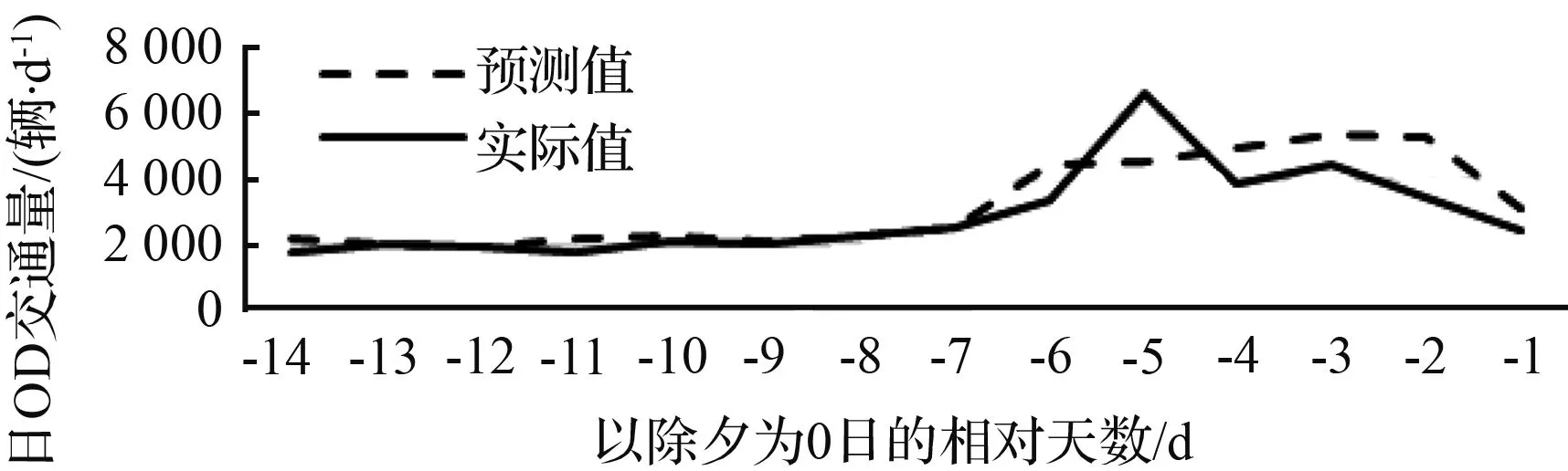
(b) 0区至7区
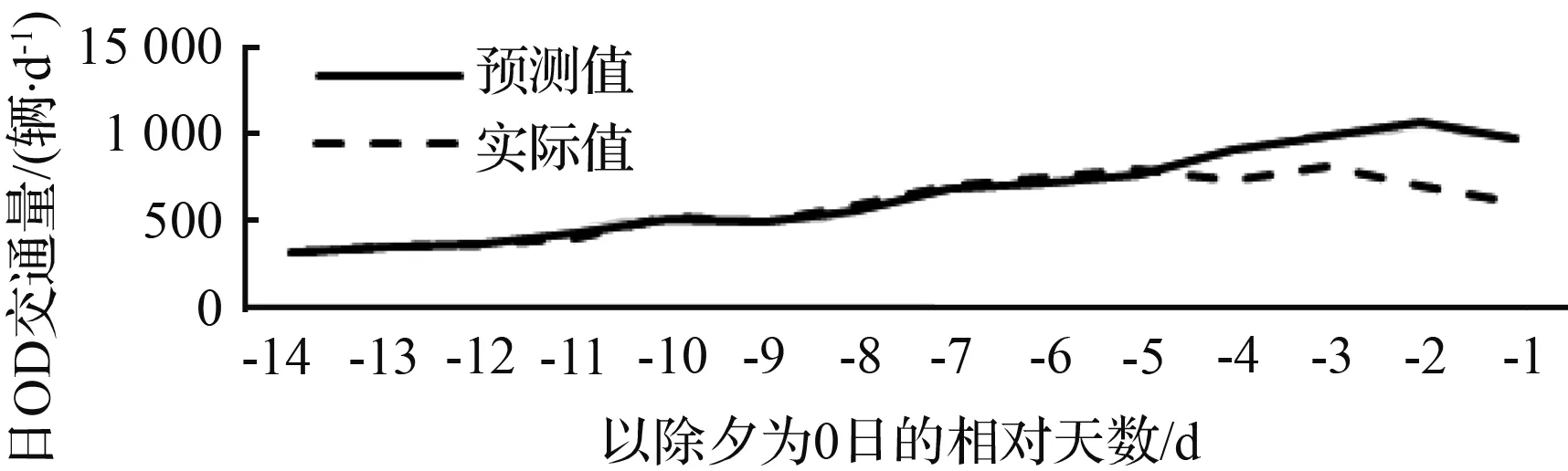
(c) 0区至10区
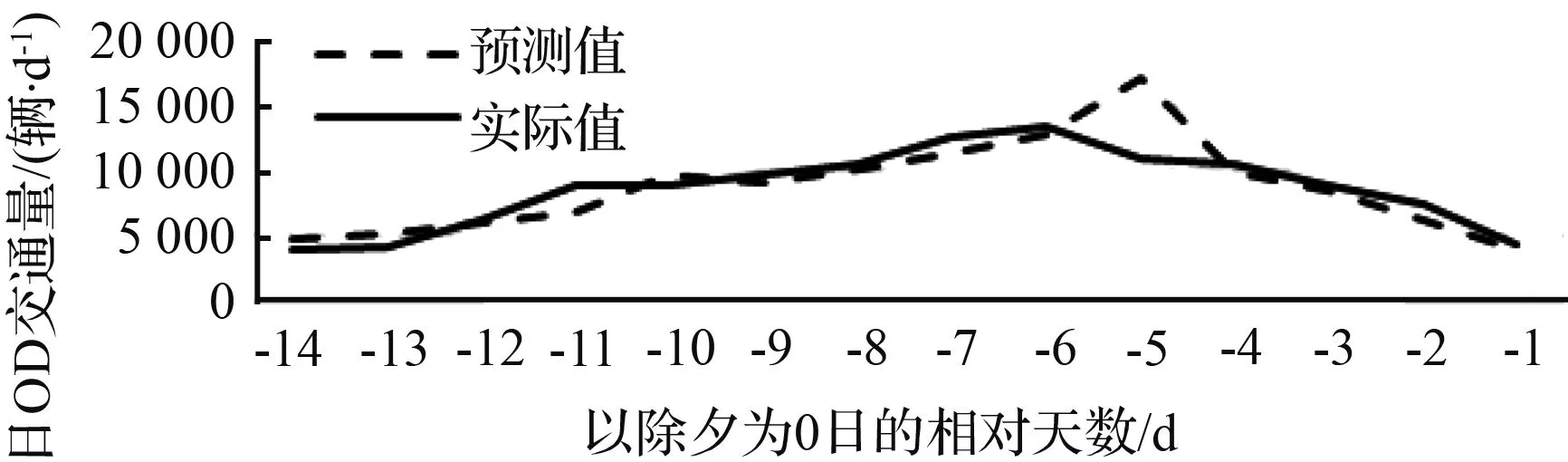
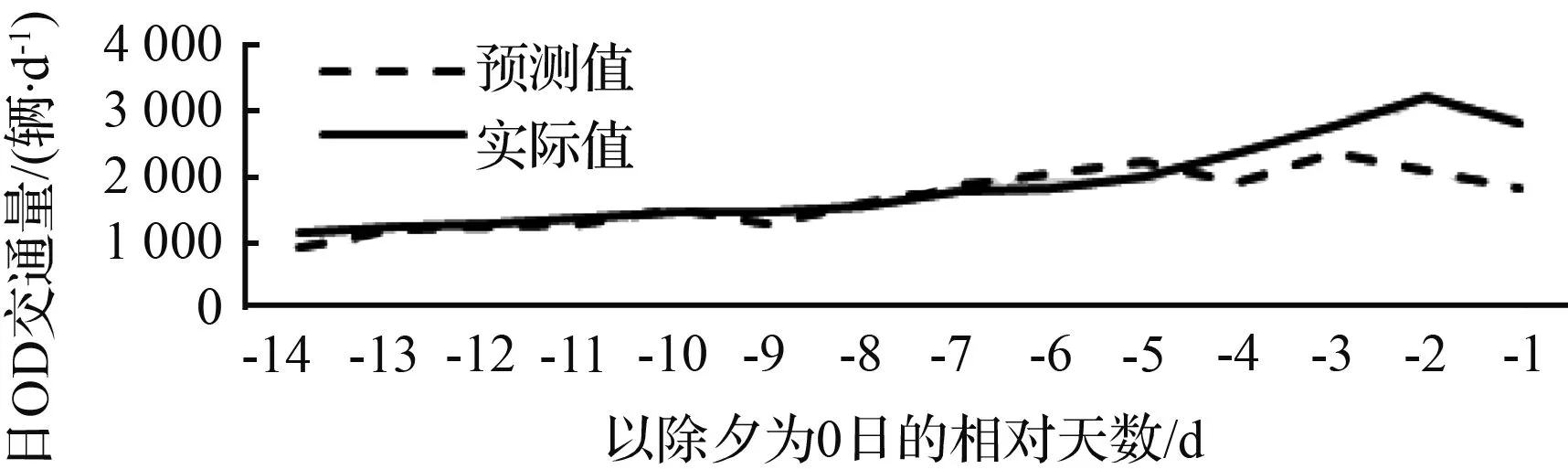
(d) 0区至20区
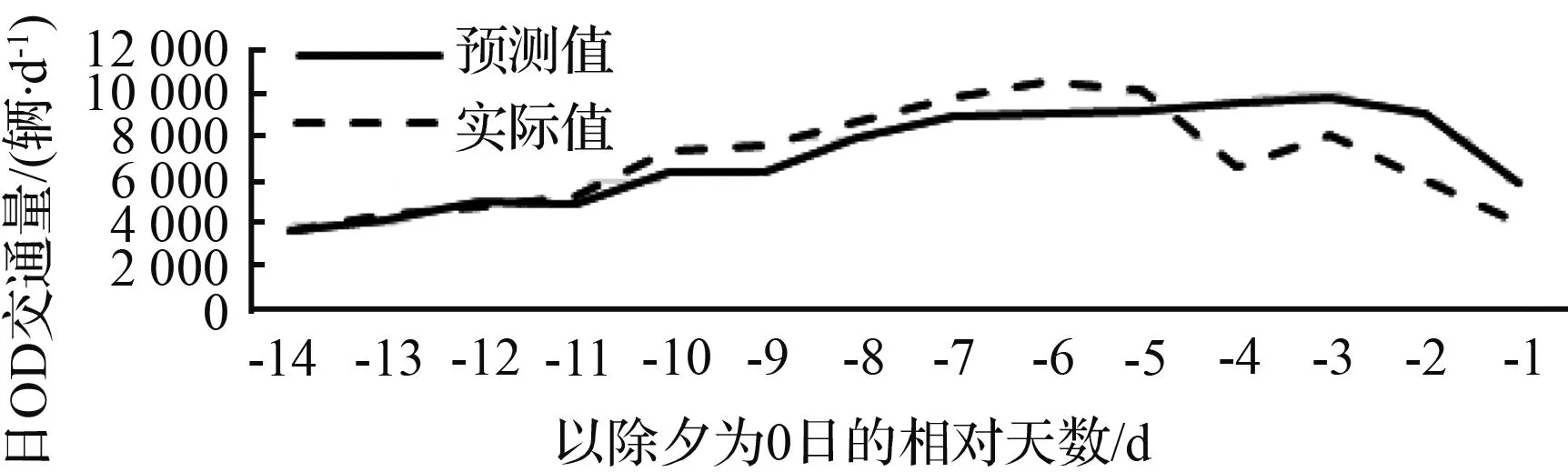
(e) 0区至21区
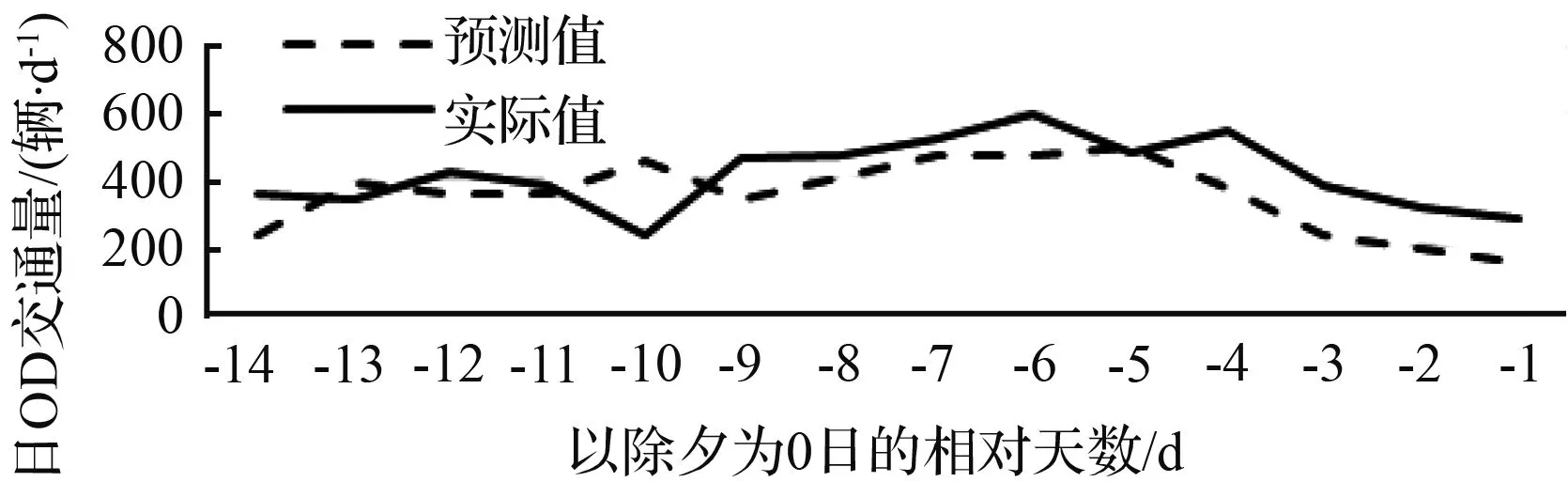
(f) 0区至22区
图3 重要起讫小区日OD交通量分布预测效果对比
Fig.3 Comparison between estimated daily OD volume distribution result and true value of important ODs
从0区至22区的预测MAPE达到35 %,但是需要注意的是该OD的节前春运日交通量维持在只有400左右的水平,由于MAPE计算公式分母为实测值,故当实测值量级较小时,即使预测值与实测值数值上偏差不大,MAPE值也会较大。从图3中可见0区到22区的各日偏差基本在100 辆/d以下,即使预测与实际值没有高度吻合,这样的数值偏差也是可以接受的。

表3 预测结果误差Tab.3 MAPE result of the proposed predition method
3 总结
本文在对高速公路历史日OD交通量分布特性进行分析的基础上,对大数据背景下的高速公路重大节假日日OD交通量分布预测的实现进行了研究,并利用广东省高速公路收费出口流水数据对算法模型进行了实验。本文的主要研究成果如下:
① 对广东省粤西高速公路路网节前春运历史日OD交通量分布特性进行了分析,并确定了节前春运的时间范围为节前两周至除夕前一天;
② 提出了先对重大节假日的总OD出行需求进行预测,再将总预测量分配到各日中的日OD交通量预测思想;
③ 在对节假日期间总OD出行需求预测方面,提出了综合考虑人口、经济发展情况、路网可达性等因素,构建多维线性回归模型的预测方法;
④ 在将总OD出行需求分配至各日方面,提出了根据历年各日占总量比例之均值作为预测分配比例的方法;
⑤ 将所提出预测方案应用于粤西高速公路2018年节前春运时段日OD交通量分布预测当中,利用实际数据对预测结果的准确性进行了验证。
动态交通分配是当下一个热门的研究方向,而欲实现动态交通分配,需要预测时变的OD出行需求,因此基于日OD交通量预测值进一步预测小时OD交通量分布是下一步研究内容。
此外,本文所提出总OD交通量预测模型尚未考虑OD交通量与OD小区间产业互补关系、用工政策等因素的关联性,因此若起讫区域间的上述因素出现较大变化,所提出模型的预测精度将可能降低,因此将更多区域间交通产生吸引影响因素纳入预测模型亦将是未来研究方向。
