一类延时时变的网络系统全局稳定性
2020-05-29陈常晖
陈常晖
(福建船政交通职业学院实训中心, 福建 福州 350007)
基于优化理论的分布式网络拥塞控制系统本质上是非线性、延时时变的[1-3]。如Steven Low、Kelly等人提出的高速网络传输拥塞控制的原始、对偶算法[4],其全局稳定性问题备受学者的关注[5-8]。文献[5]用最大的往返延时近似网络系统延时时变项, 应用Lyapunov-Krasovskii稳定性定理分析了其全局稳定性。文献[6]应用Lyapunov-Razumikhin稳定性定理分析网络系统的全局稳定性,但不考虑其延时的时变情况, 用常数的延时项代替延时的时变项。文献[7]没有忽略其延时时变的情况,采用更为严谨的数学推导,得到了低保守的全局稳定性条件。文献[8]采用解轨迹界的迭代算法获得了更好的稳定性条件。
文献[9]采用分离时滞变量、Lyapunov-Razumikhin 定理、解轨迹界方法分析了文献[4]提出的对偶算法的网络拥塞控制时滞系统的全局稳定性, 但在分析过程中没有考虑其时滞的时变特性, 用平均的往返延时近似其延时时变。
本文首先采用解轨迹方法研究了一类非线性延时时变系统全局稳定性,并将获得的结论用于分析对偶算法[4]的网络拥塞控制系统,获得了3个低保守性的全局稳定性结果。本文的主要贡献如下:1)根据文献[5-10]给出的非线性时滞网络拥塞控制系统,分析了其非线性函数和时滞变化的共同特征,凝练出能够代表上述网络拥塞控制系统的一类非线性、延时时变的微分方程。2)利用该类非线性函数是单调递减的特性,计算其在时滞区间内的最大增长率,采用倒推法计算其每一时刻的对应的更低保守的下界,从而获得了比文献[9]更低保守性的全局稳定性条件。
1 问题描述与预备工作
1.1 问题描述
先研究一类非线性、延时时变的微分方程的全局稳定性结论,再利用这个结论给出对偶算法系统的全局稳定性条件。
考虑如下非线性、延时时变系统:
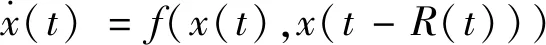
(1)
R(t)=R0+x(t-R(t))/c
(2)
R(t)≤M
(3)
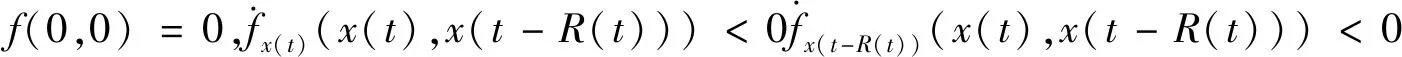
(4)
x(t)≥-α,t∈(-max(R(t)),+)
(5)
其中,f(x(t),x(t-R(t)))为连续函数[13],d>0,R0>d,c>0,α>0,M为一个充分大的正数;时滞R(t)虽然是时变的,但其变化关系满足式(2)和式(3)。假设式(1)有唯一的平衡点x0=0。
1.2 预备知识
本节给出非线性函数f(x(t),x(t-R(t)))的性质、时滞R(t)的变化规律及式(1)~(5)的解轨迹特征。
由式(4)可得f(x(t),x(t-R(t)))的如下性质:
性质1若x(t)≥0且x(t-R(t))>0 或x(t)>0且x(t-R(t))≥0, 则f(x(t),x(t-R(t)))<0。若x(t)≤x0且x(t-R(t))<0 或x(t)<0且x(t-R(t))≤x0, 则f(x(t),x(t-R(t)))>0。
下面利用时滞R(t)的变化满足式(2),式(3)给出t-R(t)与t的关系。
引理1
(a)若存在时间变量τ1,τ2,τ3, 且τ1<τ2和τ1<τ3, 若有τ2-R(τ2)=τ3-R(τ3)=τ1, 则τ2=τ3。
(b)若存在时间变量τ1,τ2,且τ1<τ2, 则有:τ1-R(τ1)<τ2-R(τ2)。
证明
(a)由式(2)知:R(τ2)=R0+x(τ2-R(τ2))/c,R(τ3)=R0+x(τ3-R(τ3))/c,
因此有:R(τ2)=R(τ3)=R0+x(τ1)/c, 所以有τ2=τ3。
(b)反证法, 假设τ2-R(τ2)≤τ1-R(τ1), 由(a)知,τ1-R(τ1)=τ2-R(τ2)不成立, 因此有τ2-R(τ2)<τ1-R(τ1)。 由式(3)知,R(t)有界。 故一定存在一个τ3, 使得τ1-R(τ1)<τ2<τ3-R(τ3)<τ3。
由式(2)知,t-R(t)是连续函数, 因此当t从τ2→τ3时,t-R(t)则从(τ2-R(τ2))→(τ3-R(τ3))。 由于τ2-R(τ2)<τ1-R(τ1)<τ3-R(τ3), 因此一定存在一个τ4∈(τ2,τ3), 使得(τ1-R(τ1))=(τ4-R(τ4))。 由(a)得:τ1=τ4, 这与τ1<τ2<τ4矛盾, 因此(b)成立。 证毕。
根据非线性函数的性质、引理1的结论, 可估计出系统(3)的解轨迹的变化特征。
定理1
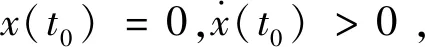
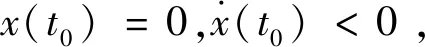
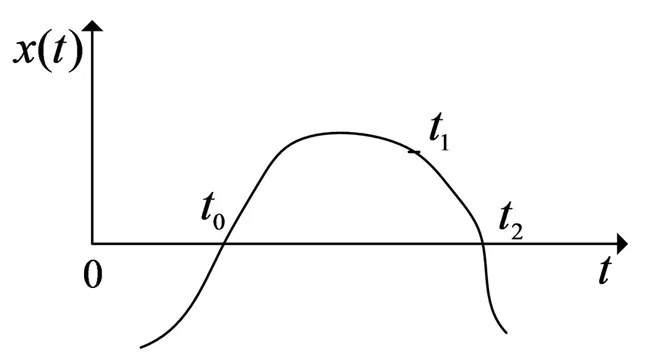
图1 系统(1)~(5)的部分解轨迹Fig.1 Part trajectories of system (1)~(5)
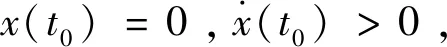
由式(1)~(5)知,x(t)、R(t)和时间变量t是连续函数变化的, 故存在t1=t0+R(t1),
s.t.R(t1)=R0+x(t1-R(t1))/c=R0+x(t0+R(t1)-R(t1))/c=R0+x(t0)/c=R0。
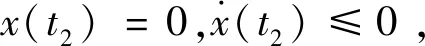
下面考虑若t∈(t0,t1], 不存在x(t)<0情况, 即对t∈(t0,t1], 有x(t)≥0。
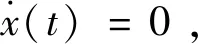
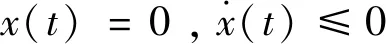
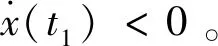
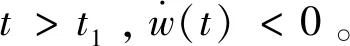
由定理1的数学描述可知系统(1)~(5)解x(t)将围绕平衡点上下波动,如图1所示。因此,将图1中轨迹每一次上下波动定义为一个波动周期,通过研究其每个波动周期上下界、及前后周期上下界的关系来研究系统(1)~(5)的稳定性。
1.3 波动周期轨迹界
根据图1,定义第i个波动周期区间:
其中
ki=2i-1,i=1,2,…
(6)
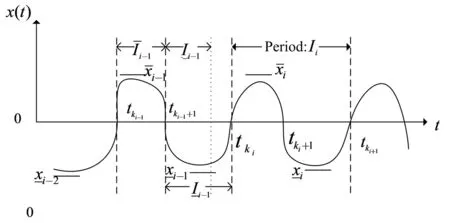
图2 系统(1)~(5)的解Fig.2 Trajectories of system (1)~(5)
对每个波动周期i,存在:
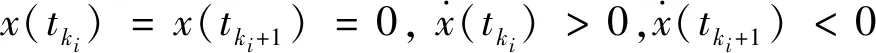
(7)
定义每个波动周期i轨迹上、下界:

(8)
对每个波动周期i,定义如下区间:
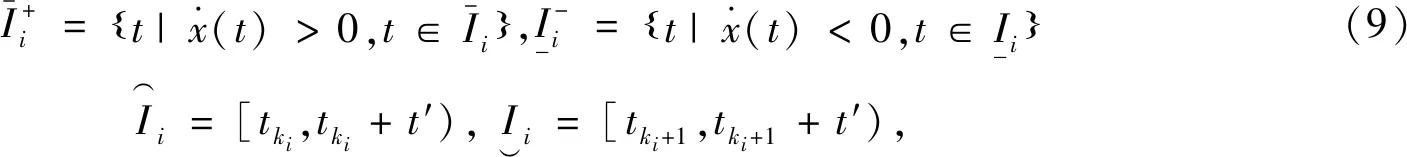
(10)
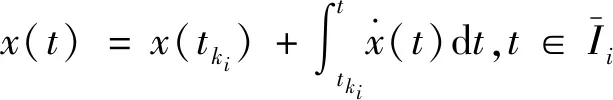
(11)
由式(7)知x(tki)=0,将式(1)右边代入式(11)得:
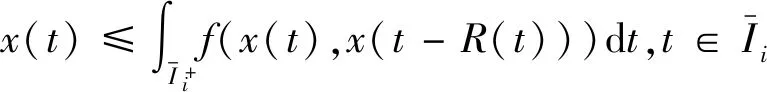
(12)
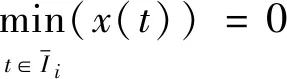
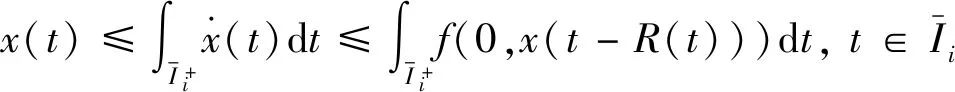
(13)
同理得:
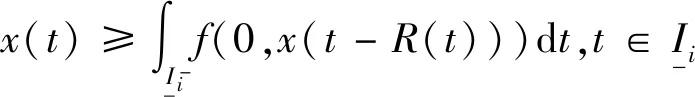
(14)
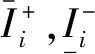
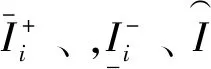
定理2
对每个周期i, 有:
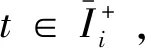
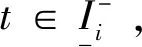
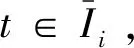
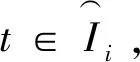
证明: (a)、(b)采用归纳法:
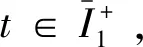
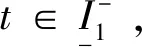
假设i-1(i>1)时成立, 即:
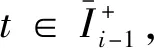
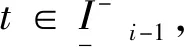
tki-tki-1>t-tki-1>R(t)≥R0
(15)
现证明i(i>2)时成立。
同理可证再向前取一个满足x(t-R(t))<0的区间也不满足。因此结论成立。
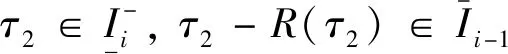
(16)
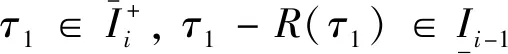
(17)
由式(16)和式(17)可得存在τ1<τ2,τ2-R(τ2)<τ1-R(τ1)情况, 这与引理2 (b)矛盾。
同理可证再向前取一个满足x(t-R(t))>0的区间也不满足。因此结论(a)、(b)成立。
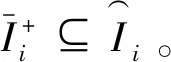
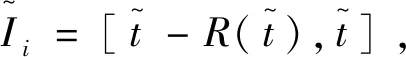
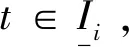
利用定理2的结论和单调递减的非线性函数的性质, 由式(13)、式(14)可计算出每个波动周期i的解轨迹上下界及前后周期的解轨迹界的迭代关系。
引理2对每个波动周期i:

(19)
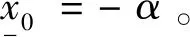
证明由式(13)和定理2(c)得:
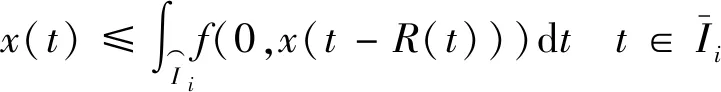
(20)
由上式可得其上界
即式(15)。
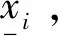
2 稳定性分析
由于该非线性函数是严格单调递减函数,因此由引理2的式(18)和式(19)的上下界的迭代关系知, 只要相关参数设置能够满足[11]:
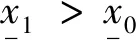
(21)
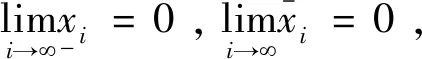
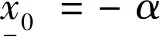
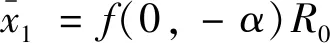
(22)
将式(22)代入式(19)得:
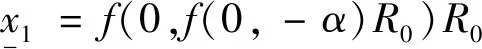
(23)
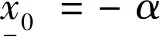
f(0,f(0,-α)R0)R0+α>0
(24)
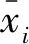
为了和式(21)、式(22)的上、下界区标记分开, 定义如下的上、下界变量:
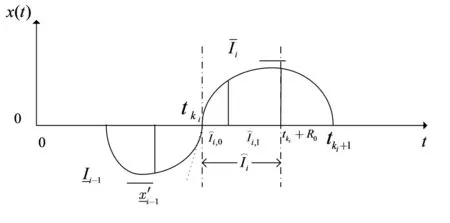
图3 积分区间的划分Fig.3 Subdivision of integral interval
为了获得每一个小区间所对应的时滞项x(t-R(t))的下界, 给出如下引理:
引理3
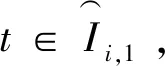
证明
(c)由式(2)知, 当t-R(t)=tki, 有R(t)=R0和t=tki+R0。
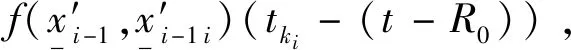
根据上式定义:
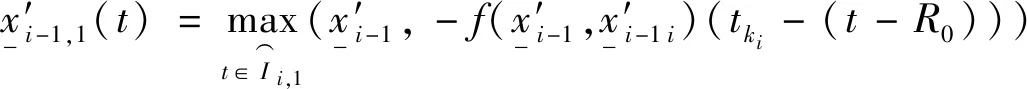
(25)
将积分区间拆分后,由式(20)得:
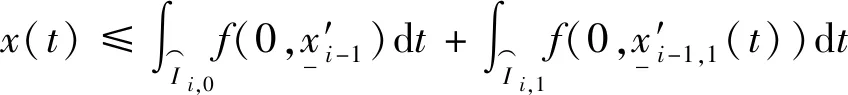
(26)
由引理3的推导过程和上式可计算出每个周期更准确的上下界:
引理4
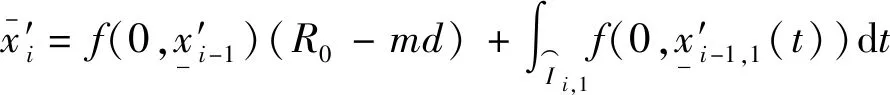
(27)
其中
(28)
定理3若
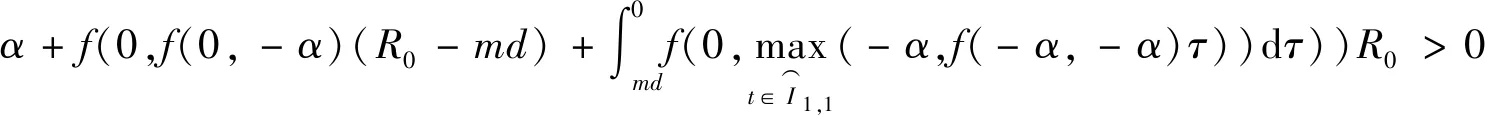
(29)
其中m∈[0,1)。则由式(1)~(5)描述的系统全局稳定。
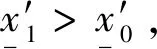
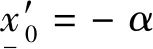
将上式带入式(24)得:
将上式代入式(25)得:
令-τ=tki-(t-R0),得
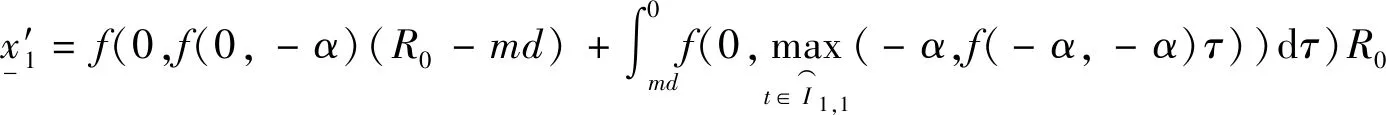
(30)
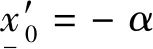
3 例证
例:考虑如下对偶算法的非线性延时时变网络拥塞控制系统[4]:
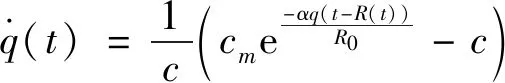
(31)
R(t)=d+q(t)
(32)
0≤q(t) (33) 其中α为控制律参数;c为链路带宽(packets/s);cm:最大速率(packets/s);d为传播延时(s);q(t)为t时刻的排队延时(s);R(t)为往返延时(s)。由式(31)、(32)得唯一平衡点q0[9-10]满足: (34) 因此有: (35) 由式(32)得:R0=d+q0[9-10]。 令x(t)=q(t)-q0,得如下非线性延时时变网络拥塞控制系统: (36) -q0≤x(t) (37) 由文献[9]和式(36)~(37)知,该系统满足式(1)~(5),故可直接调用定理3求其全局稳定性条件: (38) 由式(36)得: f(-q0)=cm/c-1 (39) 若取 md(cm/c-1) (40) 可得: (41) 将式(41)的右边代入式(38)的积分项得: (42) 将式(39)代入(42)得: 展开得: 求积分得: (43) 令 (44) 式(44)代入式(43)得: (45) 由上述推导可得: 结论2:若md(cm/c-1) 根据上述条件1~3和本文的稳定性条件计算如表1的结果。 表1 结论2的计算结果Tab.1 The calculated result of conclusion 2 由表1计算结果比较可知,在第一种情况下,条件1的α<0.83,条件2要求α<0.95,条件3要求α<1,本文结论2给出了α<1.28,得到了比文献[9]给出的3个稳定性条件更低保守的条件。 基于分布式优化理论提出的原始算法和对偶算法,在共同的约束条件下寻求自己的最优解,因此当建立相应算法的闭环非线性系统,其非线性函数特征都具有严格单调递减的特征。因此本文研究的这一类非线性延时时变网络拥塞控制系统的全局稳定性结论和研究方法,可推广到具有类似分布式优化机制的其他控制系统中去。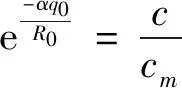
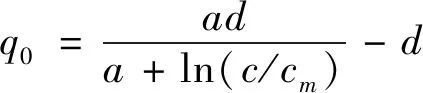
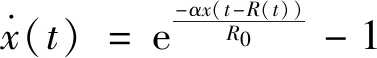
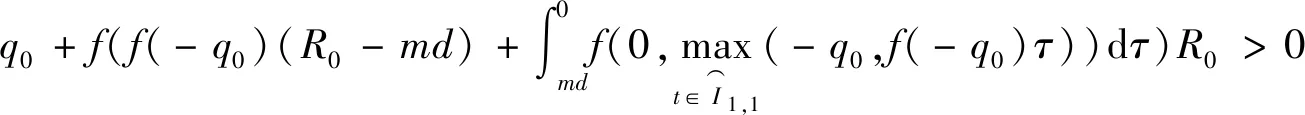
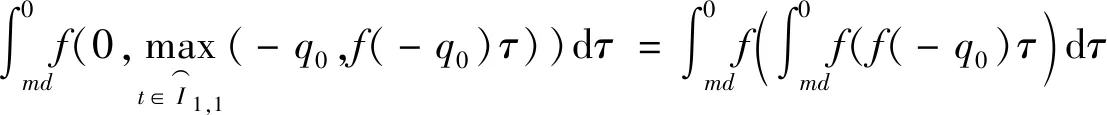


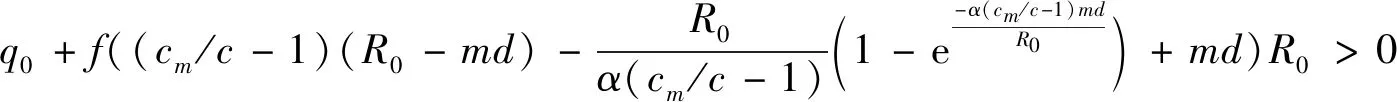
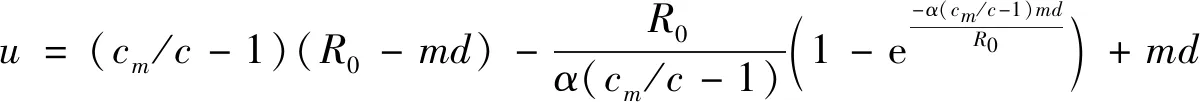
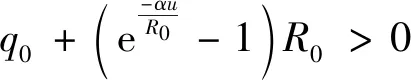

4 结论
