基于激光雷达的智能小车SLAM研究

汤 巍 王冠凌

（1.安徽工程大学电气工程学院；2.电气传动与控制安徽省重点实验室 安徽芜湖 241000）

一、引言

同时定位与地图构建(simultaneous localization and mapping,SLAM)是当今研究无人驾驶问题的热点，特别是在智能小车当中。无人车在遇到一个陌生的环境时第一个问题就是“我在哪”的问题，这就需要构图和定位。如果在一个陌生的环境中智能车（移动机器人）想要完成特定的任务，定位与地图构建的问题是首先需要解决的问题。这是一个“先有鸡还是先有蛋”的问题，移动机器人想要获得精准的自身定位信息则必须知道自身的所处环境[1]。然而想获得陌生的环境，前提是知道移动机器人自身的准确定位信息。针对这个问题，研究者提出了SLAM技术加以解决。

传感器是SLAM的核心部件。目前主流的传感器是视觉传感器和激光雷达传感器。视觉传感器有三种：单目、双目相机和深度相机。单目相机结构特别简单，成本特别便宜。单目相机拍摄的图像仅仅是三维空间的二维投影，所以无法凭借图像确定事物的真实尺度，具有尺度不确定性。由于单目相机无法通过图像确定其深度。所以人们为了得到其深度开始使用双目和深度相机。使用双目相机和深度相机的目的是通过一些手段测定物体和相机之间的距离，克服单目相机无法知道距离的缺点。知道了距离也就消除了尺度不确定性。深度相机和双目相机类似但也有所区别，因为深度相机是通过物理测量手段，而双目相机却是通过软件计算来解决，所以深度相机相比于双目相机可以节省大量的计算。但是这些视觉传感器还存在测量范围狭小、噪声大、视野小、易受太阳光干扰、无法测量透视材料的等诸多问题[2]。所以在SLAM中激光雷达传感器有更大的适用范围。相比于视觉传感器，激光雷达则不存在这些缺陷，对SLAM的应用是最好的选择。

本文智能车的同时定位与地图构建是用激光雷达作为外部传感器，并且用其采集环境信息生成环境地图；最后采用姿态位置估计算法实现对小车自身姿态和环境路标的位置估计。现阶段SLAM实现方式中稳定性可靠性好并且性能优秀的就是基于激光雷达的定位。为了解决移动机器人定位和地图的问题，最早的解决方案是卡尔曼滤波的SLAM。但是这种算法有着明显的缺点：算法的计算量过大，最后出来的估计精度也不尽人意。为了解决卡尔曼滤波的缺点，将OPTICS(ordering points to identify the clustering structure)和局部兼容数据关联的方法解决SLAM中的数据关联计算量大的问题;对数据关联后相关矩阵采用自适应渐消扩展卡尔曼滤波[3](adaptive fading extended kalman filter,AFEKF)用来替代传统卡尔曼滤波对智能车自身姿态和环境地图更新,使小车SLAM系统得到精度更高的自身位置和环境地图;最后使用MATLAB进行软件仿真实验验证了新型算法的可靠性。

（一）SLAM问题和数学表述。

1.SLAM问题表述。即时定位与地图构建的问题最通俗的说法是：移动机器人从未知环境中的未知初始点出发，移动机器人使用激光雷达传感器感知周围环境，后根据小车自身的激光雷达传感器获取的外界环境信息构建初始的环境地图，然后随着小车的移动对自身姿态和环境信息进行更新，这个问题是一个循环问题十分类似与“鸡与蛋”的问题。SLAM的模型如图所示，我们需要智能车和标志物的位置，真实的位置是没有办法被直接测量的，观察是相对于智能车和标志物之间的。

SLAM算法问题模型

2.SLAM数学描述。智能车所接受的控制指令和激光雷达所观测的外界环境是智能小车中主要的输入参数。其中控制指令有小车行驶的速度和车轮的偏转角。观测信息是周围陌生的环境信息。最终小车在行驶过程中所得到的输出信息有：小车的行驶轨迹图。SLAM在概率学的形式中，服从以下概率分布：

该概率分布描述了在已知的观察和控制输入情况下，轮式移动机器人的位置和随即在k时刻的状态的联合后验分布密度[4]。通常我们要用递归来解决这个问题。我们从时刻为k-1时的联合后验分布密度P(xk-1,m|Z0:k-1,U0:k-1,x0)开始计算，随后通过贝叶斯理论计算出控制量uk和观察量zk，最终算出这个密度。但是上述计算需要考虑出一个状态转移模型和观察模型用以描述控制输入和观察量的影响。其中观察模型描述了当机器人的位置和标志物的位置都在已知的情况时，做出观察zk的概率，我们通常把这个概率写作：

一旦我们将智能车的位置和地图都定义好，接下来我们就假设不同时刻的观察之间是相对条件独立的。此时可以将小车的运动模型用状态转换的概率分布来描述。

我们将状态转换概率假设为一个马尔科夫链，在这马尔科夫链过程中，下一时刻的状态xk的决定只由上一时刻xk-1和控制量uk所决定，而且这个状态的转换独立于观察和测绘的过程。接下来SLAM算法可以通过标准的两步递归计算出相关度（按时间顺序更新，按测量更新）更新的形式[1]：

Time-update:按时间更新

Measurement Update:按测量更新

计算联合后验分布密度P(xk,m|Z0:k,U0:k,x0)的迭代步骤如上述方程4和方程5所示。地图构建问题可以等效为计算概率密度P(m|X0:k,Z0:k,U0:k)的问题，这种等效假设小车的位置xk在所有时刻都是已知的，这样我们就可以融合地图中每个时刻的不同位置就可以确定小车的位置。同样的定位问题也可以等效看为计算概率密度p(xk|z0:k,U0:k,m)的问题,类似，为了计算小车的位置，这种等效要假设标志物的位置是已知的。

二、小车系统设计原理

智能车通过激光雷达传感器并且用改进的卡尔曼滤波算法和快速连续兼容分支定界关联算法作为智能车SLAM系统。系统采用快速联合兼容支定界关联算法[3](Joint Compatibility Branch and Bound，JCBB)，该算法比原算法获得的关联结果更加精确；对小车的姿态和环境地图的估计实现采用自适应渐消扩展卡尔曼滤波。基于激光雷达的AFEKF-SLAM系统主体框架如下图所示:

AFEKF-SLAM系统主体框架

（一）局部关联数据和OPTICS改进的数据融合算法。传感器数据的融合技术上实现困难度很大，并且这个问题一直是SLAM问题的重点和难点。它是现今无人驾驶技术提高精确度的重要方法。如今，和SLAM有关的数据融合算法主要是对参数量测和环境特征融合关联的方法如联合兼分枝定界（JCBB)算法[3];JCBB数据融合准确度高，但计算过程复杂，响应时间长。若智能车处在环境复杂的自然环境中，那么融合数据所需要的计算量是十分庞大的，即便如此JCBB算法仍然是不可或缺的优秀算法。

JCBB[5]算法相比较其他算法的优点是兼容了几乎所有观测与地图特征点，并且为了搜索兼容性最大的关联假设采用了分支定界法，其本质上是针对单变量对环境进行图搜索[6]，将所得到的环境信息进行融合。且其总体复杂度为)；除此之外，当数据进行融合并开始计算时，环境信息的计算量都与激光雷达的观测信息都与m相关，其中最为主要的是激光雷达距离标志点的距离[7]在计算中需要对刚更新的地图信息求逆运算，计算复杂度为O(m3)。所以JCBB算法的时间复杂度受：传感器观测数和已更新地图中特征点个数的影响。减少融合后环境地图特征点数和传感器观测点数可以有效的降低其空间算法复杂度，减少硬件资源的浪费，和降低以后使用的成本。所以可以对JCBB算法进行以下的改进：一是采用局部数据融合；二是采用OPTICS法对观测数和地图特征数进行聚类[3]。

1.采用局部数据融合。将需要融合的数据在地图中的局部点进行融合，这样能有效减少融合地图的特征点数，降低融合计算时的计算量，融合后的地图的局部计算复杂度为O(mn)。定义局部地图可用如下公式表示:

式中，(xv,yv,θ)表示当前时刻小车所在环境的三维坐标，(xi,yi)表示地图中标志物的平面坐标，r为传感器达最大的作用范围，Δd为范围补偿距离。

2.基于OPTICS的分组数据融合。因为传统JCBB算法需要计算整张环境地图与传感器采集的特征点数据融合[6]，所以环境的复杂度会与JCBB算法的计算量成正相关，并且计算量的增加会根据环境特征点的增加呈指数增长。因此考虑到智能车行驶在自然环境中，激光雷达传感器所观测到的特征值有显著差异，故将JCBB数据融合开始前，首先采用密度聚类方法对当前传感器输出的观测值进行分组聚类，进行分组聚类后的数据得到若干数据组；其次在每个数据组中采用JCBB数据融合算法，这样就能得到许多组数据融合组解；最后，将得到的数据融合解组获得的数据再进行融合，最终得到最优的数据融合组Hbest。

（二）基于AFEKF的小车状态和特征地图估计。传统的卡尔曼滤波SLAM有着一个缺陷:移动小车运动模型具有很强的非线性，对环境的影响是分敏感，若将该小车系统模型进行相应的简化，这样会导致传感器所采集的环境信息准确度下降，与此同时对EKF-SLAM系统的鲁棒性有很大影响，滤波并不会收敛。模型简化会使得EKF－SLAM的小车自身姿态和环境构建精度下降和收敛速度下降[7]。为了解决精确度低和收敛速度速度过慢的问题，采用一种改进的扩展卡尔曼滤波器SLAM算法，简称AFEKF－SLAM。它对小车系统采用AFEKF－SLAM的方法对环境地图进行实时更新，并通过渐消因子对地图进行有效补偿，有效改进了非线性系统的复杂度和小车行驶过程中的参数漂移对状态估计造成的影响，使得SLAM结果的准确度有所提高。

智能小车的运动模型和激光雷达扫描模型数学表达式分别为[8]:

其中，xv,t是智能车在t时刻的三维姿态，zj,t是激光雷达传感器在t时刻的距离和角度信息。L为车轴距离，v和G为t时刻系统控制输入量，dt表示输入量采样所需要的时间，v表示小车行驶速度，G是小车水平方向的夹角。(xj,yj)是激光雷所采集到环境第j个特征点的坐标[9]。

在小车运动系统中，可以将小车系统的状态向量x设置为:

其中，xv表示智能车这个时刻的状态向量，xm代表此时更新后的环境地图的向量。wt和vt分别表示为采集外界信息和观测信息，它们服从高斯分布，该高斯分布均值为0，方差为Q。

1.状态预测。根据智能车在运动过程中t-1时刻系统的运动状态xt-1、状态协方差pt-1来预测下一个t时刻的系统状态和状态协方差pt-1|t，具体计算步骤是:

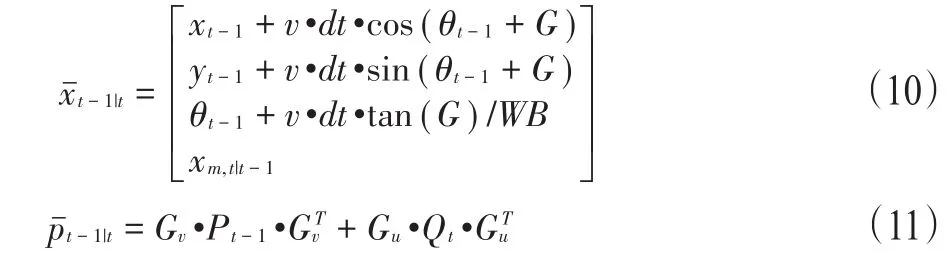
其中xt-1=[xt-1,yt-1,θt-1]T，GV和Gu为雅克比矩阵。

2.数据融合。基于前文提出的融合数据的方法得到最优的数据融合解组[10]，将当前时刻的观测量zt分为对应地图特征值的采集点zft和新的环境采集点znt，这两个采集点可以分别用来完成小车自身状态的更新和地图增广。

3.状态更新。根据观测到的小车信息zft对智能车的自身姿态和采集到的环境地图特征值进行实时更新。首先根据公式(7)中的观测模型获得观测的均值ẑt[11]，并对激光雷达传感器的观测量zft和观测均指ẑt进行比较，可以获得更新后的信息及地图的协方差，公式如下:

上述公式EKF中引入了自适应渐消因子λt，能够更好的预测误差，同时也将渐消因子引入协方差中，用增益矩阵进行在线补偿，详细公式如下所示:

上述公式中其中，Pv为小车状态向量协方差矩阵，Pm代表地图向量协方差矩阵，Pvm表示车辆运动状态向量及地图向量的互协方差矩阵。渐消因子具体计算步骤如下所示:

4.状态增广。如果小车在行驶的过程中没有观测到新的标志物[8]，则不需要进行状态增广; 如果当前时刻激光雷达观测到了新的观测量znt，那么对此时小车进行状态增广，数学处理步骤如下:

第一步小车运动过程中没有进行状态增广:

其中，znt=[rϕ]T,r为激光雷达采集到的信息到此时智能车的距离,ϕ为标志物与小车此时方向的夹角。xt=[xyθM]T,(xaug,t,yaug,t)为新观测到的特征点坐标，其计算公式如下:

状态协方差增广为:

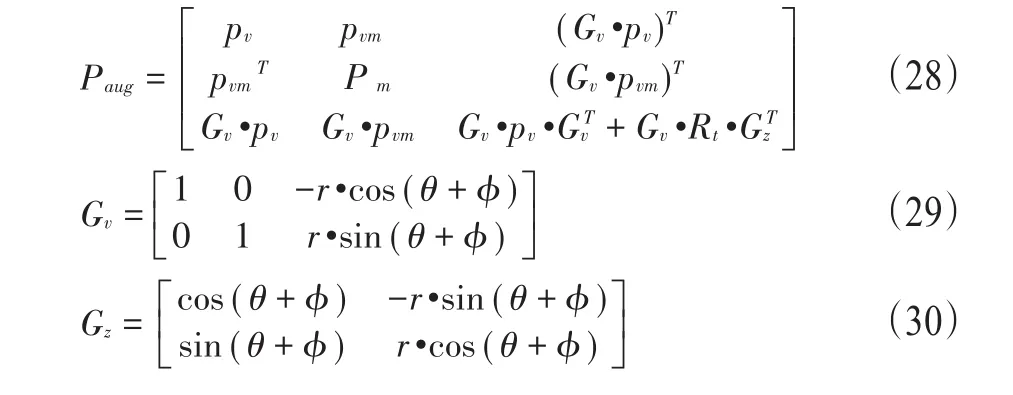
三、实验分析

本文用matlab对提出的改进卡尔曼滤波算法进行matlab仿真，并且将该算法系统得到的实验结果与传统JCBB算法融合方法的SLAM系统结果进行比较，说明改进算法的优点。

本文给出仿真实验环境如下所示，如图1所示。其中红色星号表示实验前设置的已知标志物的具体位置，蓝色星号表示利用AFEKF-SLAM算法计算出小车可能的具体位置，图中的行动轨迹表示智能小车的预先设定的路径。图中总共设定了11个地标和24个路标，传统的JCBB-SLAM算法与该机的扩展卡尔曼滤波（AFEKF）和局部数据融合移动机器人AFEKF-SLAM算法结果进行比较。

图1 移动机器人仿真环境

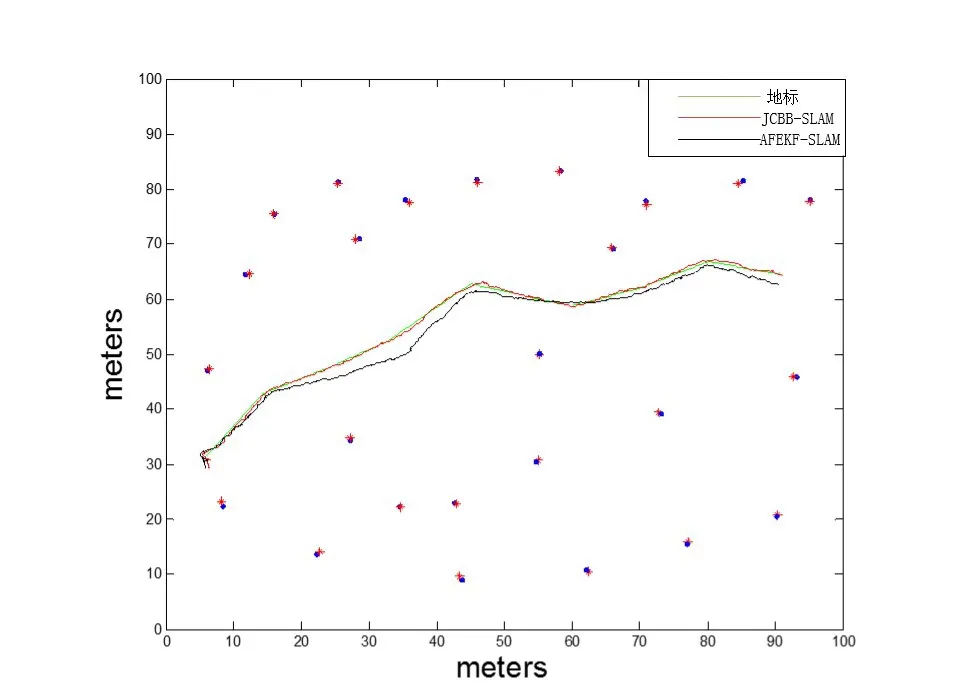
图2 实验路径跟踪图

图3 X轴误差比较

图4 Y轴误差比较

由上图的仿真结果可以看出，融合自适应渐消扩展卡尔曼滤波（AFEKF）和数据融合关联的方法与传统SLAM算法相比有更大的优势，其运动轨迹路径与智能小车真实的路径重合率更好，即预计的路标点和智能小车的位姿更加接近真实的情况和智能车的位姿，创建的地图也更加精确。由图3图4可知，本文提出算法在横坐标和纵坐标方向的估计误差都优于JCBB-SLAM算法。AFEKF-SLAM算法比JCBBSLAM算法估计的状态更加接近于真实值，从而提高了移动机器人的位姿估计精度。

四、结论

SLAM技术是智能车以及以后无人驾驶技术实现的重点和基础，本文设计了基于激光雷达的AFEKF－SLAM系统。AFEKF－SLAM系统采用改进的扩展卡尔曼滤波数据融合的方法是小车行驶的精确度更好。并且将渐消因子引入EKF中，对小车的位姿和环境信息的位置进行更加准确的估计。并对两种方法进行仿真检测。计算表明AFEKFSLAM系统复杂度低，运行效率高，且仿真结果表明AFEKF－SLAM精度要由于传统的JCBB-SLAM，其能够在不同复杂环境中为移动小车SLAM的实时性和准确性提供可靠的保证。