基于改进粒子群算法的PID参数整定分析

禹威威 申 远 王园园

（合肥师范学院电子信息系统仿真设计安徽省重点实验室 安徽合肥 230601）

一、引言

由于比例-积分-微分（Proportional，Integral and，Differential，PID）控制器[1-2]拥有结构简单、控制效果好、参数调整灵活以及鲁棒性强等诸多优点[3]，因此，近年来被广泛应用于工业过程控制和自动化生产中。在工况条件满足且确定采用的控制规律为P、I、D这种线性组合控制的情况下，其控制方法的主要表现形式为利用三个单元的校正作用对待测量参数的偏差进行整合运算，然后通过控制运算所得的输出量以控制被控对象。

由此可知，PID控制受到参数选取、被控对象系统参数以及工况的影响。但在控制器设计和应用过程中，PID参数选取具有较大难度，参数的波动影响系统的控制效果，因此，研究PID参数优化具有重要的理论和工程意义[4]。

目前，研究学者针对PID控制器参数优化已开展了较多研究[5-9]。在文献[7]中，无需改变现有控制回路的正常运行状态，只要对通过控制回路的输入输出数据进行处理，即可获得重要临界频率响应特性，然后在线辨识过程对象并采用基于Z-N的方法更新PID控制器参数。所提方法性能比传统的Z-N法优越，曲线更理想，但仍具有一定的局限性，需要事先确定期望值和相角，不具灵活性，缺乏优化空间。文献[8]提出了基于梯形隶属函数的模糊切换算法及仿人智能思想的优化改进算法，并将其应用于温度控制系统中实现自适应的模糊PID参数整定。此算法结合了二者的优点，使系统具有较好的稳定性、动态性、无静差等优点，但缺点也比较明显，主要体现在隶属函数规则复杂，算法过程复杂，精度不高。文献[9]用改进遗传算法对PID控制参数进行优化，其中所做的改进包括分别对算法程序中的交叉、变异环节做自适应处理，用来提高算法效率和系统性能。所做改进在优化结果的质量与执行效率方面都具有较好的控制效果，但同时也增加了过程的计算量，解码过程也相当复杂。

基于以上分析可知，PID参数优化既要使调整出来的控制器具有理想的效果，又不希望优化过程复杂，计算量大，且耗时耗力。因此，粒子群优化（Particle Swarm Optimization，PSO）算法因其过程简单，易收敛，速度快等诸多优点[10-11]进入了研究者的视野。但同时也因其存在易早熟收敛陷入局部最优的问题，文献[12-13]的作者提出了杂交PSO算法的概念，在整定过程中引入随机杂交概率；文献[14]则引用了变异概率来克服算法易陷入局部最优的缺陷。虽然文献[12-14]中针对PSO算法的改进扩大了粒子的多样性，提高了全局搜索的能力，但并未考虑引入的杂交和变异算子对算法稳定性的影响。

因此，本文在借鉴遗传算法中交叉和变异机制的同时引入精英保留的思想，保留最优个体，避免引入杂交和变异操作引起的算法的不稳定性，提高全局搜索能力的同时，提高全局收敛速度。

二、基于改进PSO的PID控制器的设计

（一）适应度函数选取。通过选取绝对误差时间积分(integral time absolute error，ITAE)指标作为适应度目标函数，以体现PID 控制器的优化效果，即

式中，Jmin为ITAE性能评价指标，越小代表系统性能越好；e(t)为输出与输入之间的误差；t为时间。

（二）基于改进PSO的PID控制器设计。通过选取绝对误差时间积分(integral time absolute error，ITAE)指标作为适应度目标函数，以体现PID控制器的优化效果，即

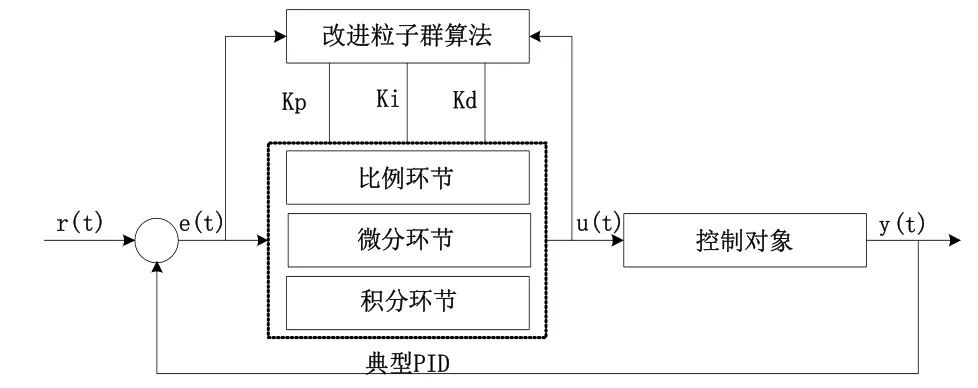
图1 基于PSO的PID控制器系统结构图

其中，改进粒子群算法将在下一章节详述，此处不再赘述。而典型的PID控制器一般形式可表示为

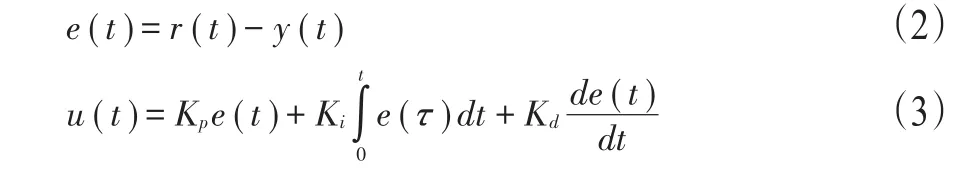
式中，r(t)、u(t)和y(t)分别为输入、控制器输出以及系统输出；Kp、Ki和Kd分别为比例、积分和微分系数。

在控制系统设计和仿真中，也经常写成传递函数形式：

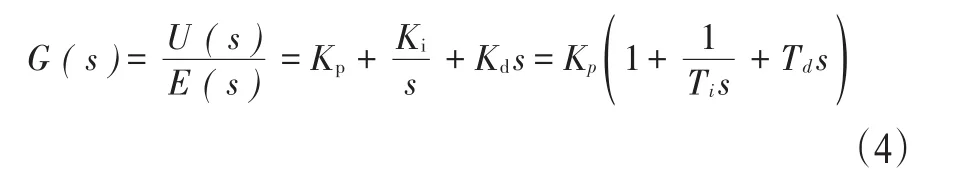
其中，Ti为积分时间常数，Td为微分时间常数。

三、基于改进PSO的PID控制器的优化算法设计

（一）标准粒子群算法。标准粒子群算法是Shi.Y等人于1998年在最初版的PSO基础上提出的增加了惯性权重系数w的改进算法，其目的主要是平衡局部优化和全局优化能力[15-16]。这主要是因为w设置得较小时局部搜索能力更强，而较大是全局搜索能力更突出。如公式（5）所示

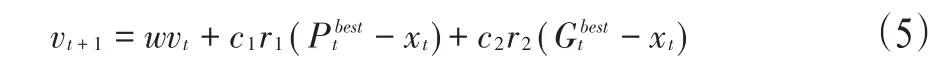
其中，vt和vt+1分别表示粒子更新前/后的速度；c1、c2为加速常数；r1、r2为产生的随机数；分别为粒子的个体最优位置和全局最优位置；xt表示粒子x更新前的位置，其更新公式可表示为

若将w设定为某一固定值，则需要根据实际情况判断，若小了容易陷入局部优化，若大了则不利于极值收敛。因此，为解决这一问题，提出了线性递减惯性权重（linear decreasing inertia weight，LDIW），w随着优化迭代增加而改变，其公式为

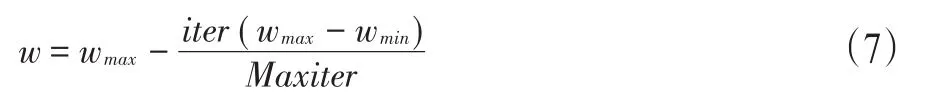
式中，wmax、wmin、iter和Maxiter分别为最大权重值、最小权重值、当前迭代代数和最大迭代数。

（二）粒子群算法的改进。改进粒子群算法是在标准粒子群算法的基础上引入遗传算法中的杂交和变异概率以扩大种群的多样性，防止算法过早陷入局部收敛；同时为避免引入的杂交和变异操作影响算法的稳定性，不利于算法的全局收敛，采用精英保留策略，对个体适应度值进行排序，优先选择个体适应度值较高的个体。

具体的过程如下：

1）赋予每个粒子随机数r1和r2，通过判断随机数是否小于等于杂交概率和变异概率决定当前粒子是否进行杂交、变异操作；

2）被选中的杂交个体，随机选择群体中的另一个粒子进行杂交，子代粒子的位置由父母代进行公式（8）操作来计算；

3）被选中的变异粒子通过变异以产生更优秀的个体，变异操作方法为：

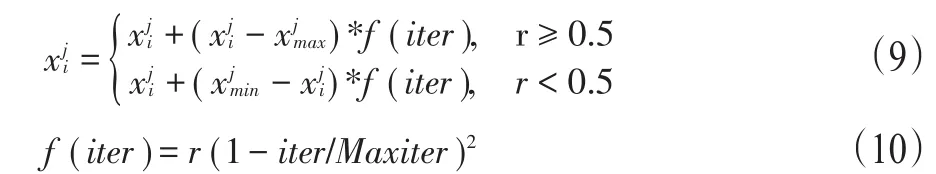
4）对通过交叉和变异之后的粒子进行边界检测，对于超出边界的粒子位置，在标准粒子群算法中一般直接将其限制在边界位置，伪代码如式（11）所示。但在本文中，对于交叉变异操作后超出边界的粒子，不以边界对其约束，而是以式（12）所示的方式产生新变异的粒子替代超出搜索区域的粒子。当进化过程出现停滞或出现早熟收敛时，就能够跳出当前的位置，进入其他区域进行搜索。

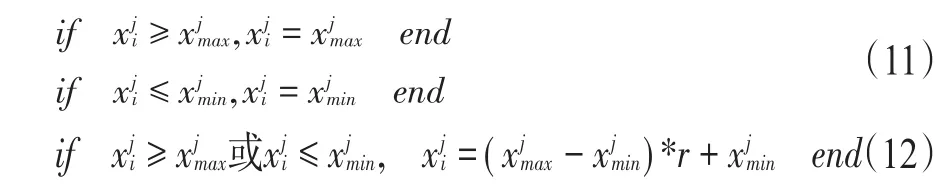
5）以上交叉和变异操作的粒子因为其跳跃性搜索而使种群的多样性得以维持，但也可能会造成最终收敛到全局最优比较困难，因此作者将精英保留的思想应用到此改进PSO算法中，以避免最优个体的信息丢失。假设种群的精英个体数为种群的1/4，在迭代进化过程中，对迭代更新变化后种群和精英种群合并排序，剔除排序靠后的1/4个体，并将排序靠前的1/4个体的速度、位置以及适应度值替代旧的精英个体。

（三）优化设计过程。基于改进PSO对PID控制器的参数进行优化设计，具体流程如图2所示，主要步骤为：

步骤1）设置算法初始参数（c1、c2、w、交叉概率pc、变异概率mut、精英数目elitnum、总群数pop、参数范围等），初始化个体的位置和速度。

步骤2）调用Simulink部分的PID_model文件，将算法程序中的未知参数依次传递给PID控制器的三个参数Kp，Ki，Kd；然后运行控制系统的PID_model模型；最后，输出绝对误差时间积分ITAE，传递至PSO算法程序中。

步骤3）初始适应度值极值排序，确定初始个体最优粒子和初始全局最优粒子；确定初始种群精英个体。

步骤4）执行（4）（5）速度和位置更新操作，使用标准粒子群算法常用方法限制粒子更新速度和优化范围，调用步骤2）部分，计算个体ITAE。

步骤5）然后选择父母粒子进行杂交和变异操作，若交叉变异后的子代计算得到的个体适应度值优于父母粒子的适应度值，则直接替换父母代粒子，否则重新进行交叉变异操作。

步骤6）对更新后的粒子和精英粒子组合排序，选取前pop个粒子作为下一代粒子，选取前elitnum个粒子作为当前精英粒子，并更新个体的最优粒子和全局最优粒子。

步骤7）最后根据ITAE是否满足条件或是否达到最大迭代次数，若满足条件，则退出算法，得到最优解集；若不满足，则按顺序执行步骤4）至步骤7）。

四、仿真分析及实验对比

通过仿真实验对所提方法进行测试，在仿真分析软件Matlab上编写改进PSO算法程序，同时在Simulink系统中搭建PID模型文件。选取二阶纯滞后被控对象，传递函数如下：

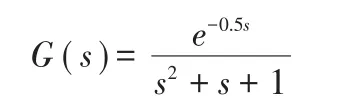
设定的标准粒子群算法的初始参数如下所示：粒子数pop为40；最大迭代次数为100；Kp，Ki，Kd三个参数的位置搜索范围为[0，5]，速度范围为[-0.1，0.1]；学习因子c1=c2=2；惯性权重从0.95到0.1线性下降。改进的PSO算法在标准粒子算法的基础上增加杂交概率pc为0.75，变异概率为0.08，精英个体数设定为10。另外，再将改进的PSO算法与普通遗传算法的PID控制效果相比较，设定其杂交概率为0.9，变异概率为0.1。

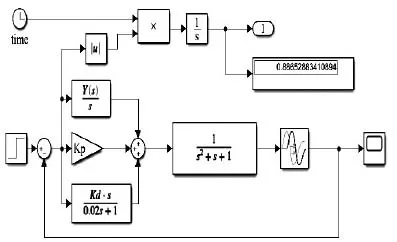
图2 PID仿真模型

PID仿真模型如图2所示，输入信号为单位阶跃信号，设置的采样时间间隔为0.001s，仿真时间为20s。经过100次迭代后的三种方法的PID参数收敛图以及单位阶跃响应比较图分别如图2、图3所示。

从图2的三种不同控制算法的函数收敛趋势曲线图可得出，由于交叉和变异概率的引入使得改进粒子群算法虽然收敛速度不如标准PSO，但还是比遗传算法的收敛速度更快，能有效找到最优结果，且其目标函数ITEA的搜索结果明显优于其他两种算法的整定结果。

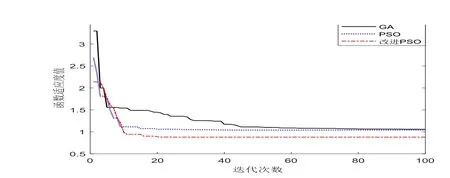
图3 适应度函数收敛曲线

图4 单位阶跃曲线图

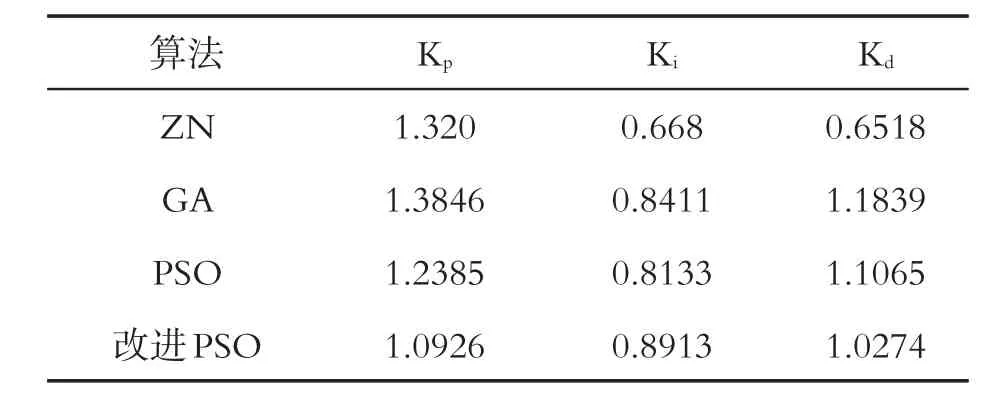
表1 不同算法的PID参数对比

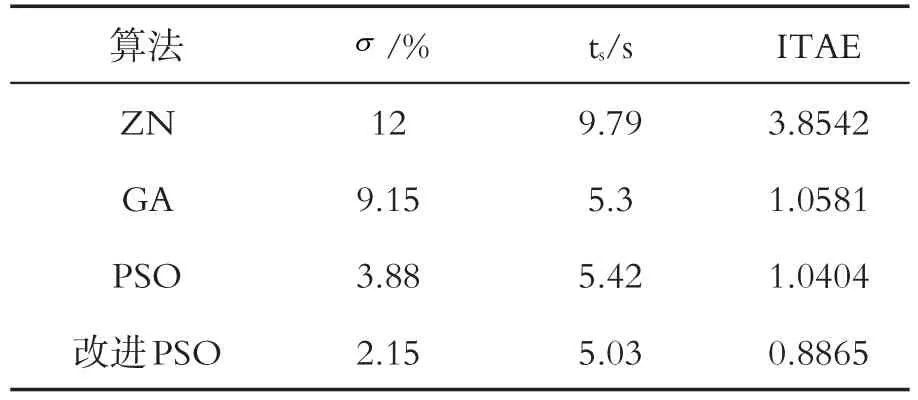
表2 不同算法的PID控制性能对比

表1为四种不同控制算法的Kp、Ki、Kd三个整定参数；表2为性能指标超调量、整定时间和ITAE（绝对误差）的比较。

由上图和上表可知，与其他三种方法整定的控制效果相比较，改进PSO的PID方法得到的系统最大偏差最小，达到稳态值+2%的时间最短，系统的调节的速度更快，控制性能最优。

五、结论

本文基于改进PSO对PID控制器参数进行整定分析与研究。通过将交叉、变异概率应用于标准PSO算法中，能有效克服未改进前的早熟陷入局部收敛的问题。同时为避免引入的杂交和变异操作影响算法的稳定性，作者引入精英保留思想，提高算法的稳定性和最终结果的全局收敛性。最后，通过实验证明此改进PSO算法的整定控制效果优于传统的ZN整定以及标准PSO以及遗传算法，具有一定的推广价值和应用前景。