基于分治法及排队论的机场出租车问题研究*

吴云标 王 帅 牛天宇 章 行

(1 皖江工学院基础部；2 皖江工学院机械工程学院 安徽马鞍山 243031)

机场陆侧交通系统在衔接机场交通和城市交通中发挥十分重要的作用[1].出租车作为一种重要的衔接方式而受到了广泛的研究.目前研究主要集中在对机场交通系统运行的分析与评价，其研究内容也主要集中在对出租车下客区和上客区的通行能力及服务水平[2-3]，在对机场出租车司机收益和机场乘客区上车点的设置、车辆与乘客的安排等问题上研究相对较少.鉴于机场出租车司机收益问题，机场乘客区经常会出现出租车排队载客和乘客排队乘车的情况，文章基于出租车选择决策以及排队论模型，以南京禄口国际机场为例，对出租车司机排队等待或空载返回提供了选择方案，并对乘客区上车点、出租车和乘客的安排进行研究，在保证车辆与乘客的安全下，使得总的乘客效率到达最高，减轻机场客流量所带来的压力.

1 出租车司机选择决策模型的构建

1.1 影响出租车司机决策的因素分析

出租车司机的决策受到多方面因素的影响既有时间成本，也有资源成本.时间成本与等待时长存在数量关系，等待时长排队出租车以及乘客的数量，资源成本含有可能损失潜在的载客收益和空载费用.当出租车司机选择排队等候时，排队等候的出租车数量和乘客的数量会影响出租车等待的时长，存在时间成本.当出租车司机选择放空返回到市里，会产生空载费用和可能损失潜在载客的收益，存在资源成本.文章综合考虑了两类成本对出租车司机决策的影响，其关系如图1所示.

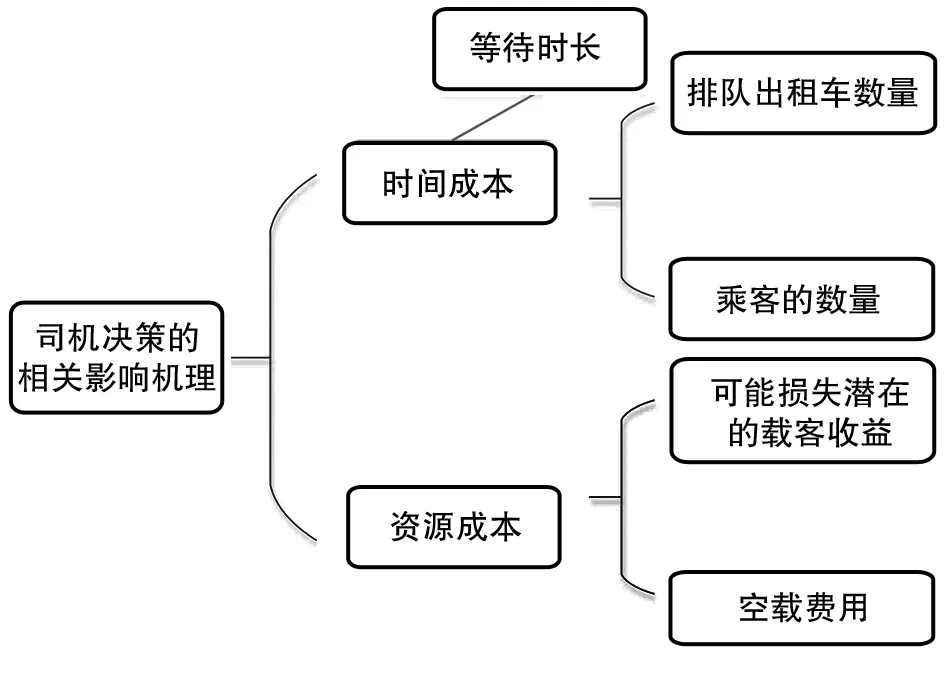
图1 影响出租车决策的因素关系图

1.2 分治法数学模型

分治法[4]是计算机科学中一类重要的算法，可以简单的解释为将一个整体分成若干个小部分，分别对这些小部分进行独立的求解，然后将各自所得解归纳合并.

1.2.1 出租车数量对出租车司机的决策的影响 若出租车司机选择放弃返回市区拉客，则可按下式计算资源成本：

S=M+G

(1)

其中，S是资源成本，M是空载费用，G是可能损失潜在的载客收益.

资源成本S等于最大时间成本Cmax：

Cmax=S

(2)

出租车在机场“蓄车池”等候的时间tmax为：

(3)

其中，tmax是出租车在机场“蓄车池”等候的时间，d是出租车单位时间里损失的利润，Cmax是最大时间成本.

计算出“蓄车池”里最多能停留出租车数量Lmax，保证时间成本小于资源成本：

(4)

其中，Lmax是“蓄车池”里最多能停留出租车数量，tmax是出租车在机场“蓄车池”等候的时间，Tp是每辆停留载客的时间.

通过上述的计算公式计算出“蓄车池”里最多能停留多少出租车Lmax，完成了出租车数量对出租车司机的收益考虑.

1.2.2 乘客数量对出租车的决策的影响

乘客数量会对出租车数量产生影响.假设一个人上一辆车，则第N个人上第N辆出租车.则第N辆车等待时间的成本C1：

C1=t1×d

(5)

其中，t1是第N位乘客等待时间，其计算如下：

t1=Tp×N

(6)

第N辆车载送第N位乘客所获得的利润为S，若S>C1，则出租车司机选择去“蓄车池”等候排队，即：

S-TpNd>0

(7)

通过上式可算出L的临界值Nmax.当出租车数超过Nmax时，可选择空载返回市区.反之，则留下等候排队.

2 南京禄口机场出租车司机决策相关因素的量化分析

2.1 数据来源

数据来源于南京禄口国际机场官网.通过南京禄口国际机场至市内代表性目的地相关出租车数据，将所得到的数据进行整理得到表1.

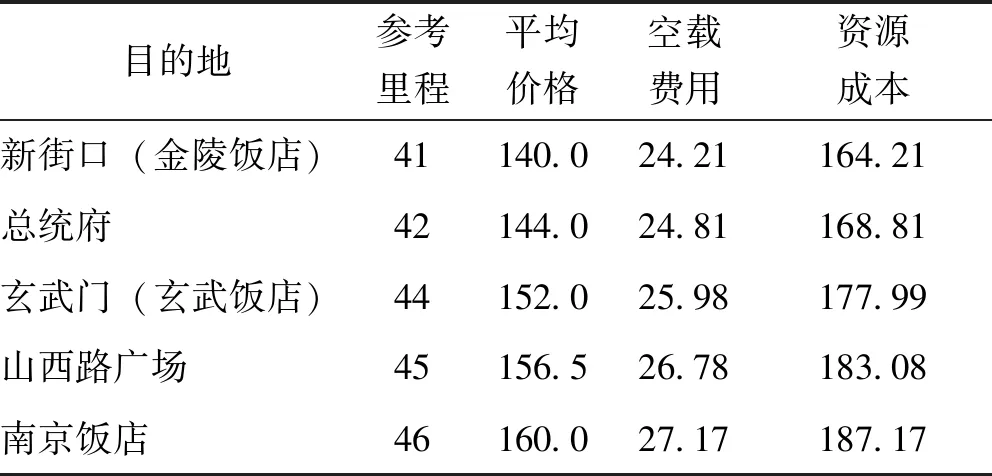
表1 禄口机场至市内代表性目的地出租车资源成本

根据南京出租车上的价目表计算所得行驶一小时所获得的大约收益是d=160.58元/时(超过3公里).“蓄车池”的每辆车停留载客的时间TP=29.8s.

2.2 结果分析

2.2.1 出租车数量对司机决策分析 以南京禄口国际机场到新街口(金陵饭店)为例.通过表1得到新街口(金陵饭店)资源成本：

S=M+G=164.21

资源成本(S)等于最大时间成本(Cmax)：

Cmax=S=164.21

出租车在机场“蓄车池”等候的时间(tmax)：

计算出“蓄车池”里最多能停留出租车数Lmax，保证时间成本小于资源成本：

说明当该出租车少于124辆车时，选择去“蓄车池”等候排队；若超过124辆车，则选择空载返回市区拉客.

2.2.2 乘客数量对出租车决策分析 以南京禄口国际机场到新街口(金陵饭店)为例.第N位辆车等待时间的成本C1：

C1=t1×d=Tp×N×d=1.3291N

则由S-TpNd>0可计算出Nmax≈124.

说明从南京禄口国际机场到新街口(金陵饭店)乘客人数的最大值为124人.当乘客数量小于124人次时，出租车应选择去“蓄车池”等候排队；若乘客人数大于124人次时，则应选择空载返回市区拉客.

3 基于排队论M/M/S模型对乘车区上车点安排的研究

排队论M/M/S模型[5]是一种研究系统随机聚散现象和随机服务的系统，对服务顾客到来和提供服务时间的统计研究，得出一些数量的指标，比如服务顾客等待时间、系统的状态、服务顾客的期望队长、平均逗留时间等.

上车点J为：

(8)

其中，V是在行驶候车区汽车行驶的速度，S1是候车区路长.

平均乘客到达率α为：

(9)

其中，Nα是单位时间内平均到达乘客数量，Tα是单位时间.

平均乘客服务率β为：

(10)

其中，T是单位时间.

根据M/M/S模型输入的乘客源是没有上限的，乘客是随机，单个到达，到达的过程服从Poisson分布，具有平稳性.排队规则是单队，队伍的长度是没有上限的，服从先到先服务.服务平台的服务时间是随机的，服从指数分布.整个系统的平均服务率为αJ，系统的服务强度γ：

(11)

运算的状态概率：

(12)

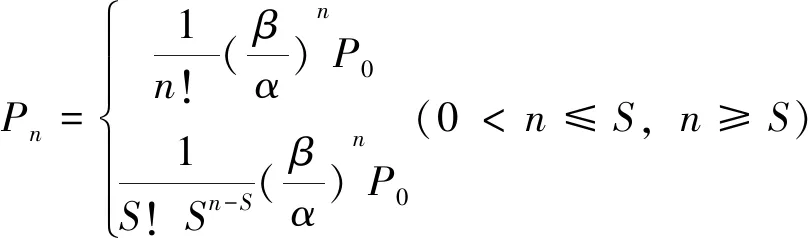
(13)

运行指标：

(14)

(15)

Ls=Lq+Sρ*

(16)

(17)

程序系统状态N≥S的概率：

(18)

通过以上可以计算出等待乘客数量，进而可以计算出租车的需求数量.

4 结语

文章建立了出租车司机选择决策模型体系，综合考虑乘客数量与出租车收益的方面，将影响决策的主要因素时间成本和资源成本带入模型中.并以南京禄口国际机场为例，计算单位时间内蓄车池中最大停车辆的临界值，当小于临界值则选择等待载客，反之空车回市内载客.对于乘车区上车点的安排问题，文章采用了排队论模型，建立了等待时间与停留时间、到达时间和离开时间的评价指标.该模型体系可以给机场出租车司机对载客的决策以及机场相关部门对于乘车区上车点的设置、乘客与车辆的具体安排提供参考依据.