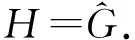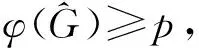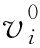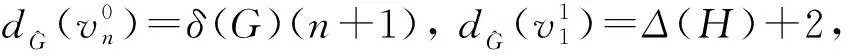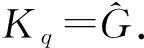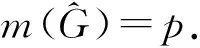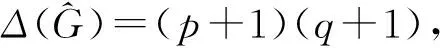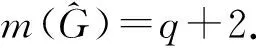图的冠积和边冠积的b-染色
2020-05-29田双亮索郎王青
杨 青, 田双亮, 索郎王青
(西北民族大学 数学与计算机科学学院, 兰州 730030)
1 引言与预备知识
在图染色中, 通常研究图元素的最小分类问题.但还有一类染色研究图元素的最大分类问题, 如b-染色[1]与Achromatic-染色[2]等.b-染色是在Achromatic-染色基础上提出的染色概念, 关于b-染色的研究目前已有很多结果[3-10]: Vivin等[3]研究了任意两个图的冠积可b-染色, 并给出了任意图与其同阶路、圈、完全图的冠积b-色数; 在文献[3]的基础上, 代天骄等[4]研究了路、圈与完全图的冠积的m-度与b-色数; 吕闯等[5-6]研究了路、圈、轮等所构成的冠积的m-度与b-色数.关于图的广义冠积和广义边冠积的研究可参见文献[11-12].本文主要研究图的冠积和边冠积的b-色数, 并在此基础上推出广义(边)冠积的b-色数.
本文讨论的图均为简单图, 分别用V(G),E(G),Δ(G),δ(G)表示图G的顶点集、边集、最大度和最小度, 用dG(v)表示G中顶点v的度数,Nr(v)表示顶点v相邻的r个顶点的集合, 其中r≤dG(v).设σ为G的一个k-正常染色, 用S(A)表示A中顶点颜色的集合,Si(G)表示G中颜色为i的所有顶点的集合, 其中A⊆V(G)且i∈{1,2,…,k}.记[n]={1,2,…,n}.本文未说明的符号及术语可参见文献[13].
定义1[1]设{V1,V2,…,Vk}为图G的一个k-正常点染色, 若对任意的i∈{1,2,…,k}, 存在b-点ν∈vi, 使得{v}∪Vj为非独立集, 其中j=1,2,…,k且j≠i, 则称该点染色为图G的一个k-b-染色, 最大的k值为图G的b-色数, 并记为φ(G).
定义2[1]设图G的顶点集为V(G)={v1,v2,…,vn}且
dG(v1)≥dG(v2)≥…≥dG(vn),
称m(G)=max{1≤i≤n,dG(vi)≥i-1}为图G的m-度.
根据上述定义, 显然有如下结果:
引理1对任意图G, 有
χ(G)≤φ(G)≤min{Δ(G)+1,m(G)}=m(G).
对任意两个图G与H, 设V(G)={v1,v2,…,vn},E(G)={e1,e2,…,ek}, 若对H有n次拷贝, 将第i次拷贝的Hi所有顶点与G中顶点vi连接, 其中i∈[n], 这样构造的图称为G与H的冠积[14], 记为G∘H.若H有k次拷贝, 将第j次拷贝的Hj所有顶点与G中边ej的两个端点连接, 其中j∈[k], 这样构造的图称为G与H的边冠积[15], 记为G◇H.
2 图的冠积的b-染色
定理1设G与H分别为p阶与q阶的简单图, 若
Δ(H)+1≤p-δ(G)-1≤q,
则φ(G∘H)=p.

由
Δ(H)+1≤p-δ(G)-1≤q,
有
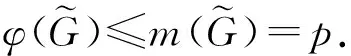

根据定理1, 可得如下结论:
1) 若n≥6且i≥-3, 则φ(Cn∘Cn+i)=n;
2) 若n≥5且i≥-2, 则φ(Pn∘Pn+i)=n;
3) 若k≥s≥t≥4, 则φ(Kt,s∘Ck)=s+t,φ(Kt,s∘Pk)=s+t.
由Δ(Cn+i)=δ(Cn+i)=2及定理1, 有3≤n-3≤n+i, 因n≥6且i≥-3, 显然不等式3≤n-3≤n+i成立, 即φ(Cn∘Cn+i)=n; 由Δ(Pn+i)=2,δ(Pn+i)=1及定理1, 有3≤n-2≤n+i, 因为n≥5且i≥-2, 显然不等式3≤n-2≤n+i成立, 即φ(Pn∘Pn+i)=n; 由
Δ(Ck)=Δ(Pk)=2,δ(Kt,s)=t
及定理1, 有3≤s+t-t-1≤k, 即3≤s-1≤k, 因为k≥s≥t≥4, 则
φ(Kt,s∘Ck)=s+t,φ(Kt,s∘Pk)=s+t.
根据定理1, 可得满足定理1中约束条件图类的广义冠积的b-色数.
推论1设G为p阶图,hp=(Hi)i∈[p]为q阶不相交图序列, 记max{Δ(Hi)|i=1,2,…,p}=Δ, 若Δ+1≤p-δ(G)-1≤q, 则G与hp的广义冠积G∘hp的b-色数为p, 即φ(G∘hp)=p.
由定理1可得部分简单图的冠积的b-色数, 但还存在某些简单图不满足定理1的约束条件, 如任意两个同阶图或完全图的冠积b-色数.
引理2[3]设G与H均为n阶图.若Δ(H) 证明: 当Δ(H) 根据引理2, 可得文献[3]中提出的任意图与其同阶的路、圈的b-色数, 即文献[3]中定理3.1、定理4.2和定理5.2.此外, 还可得如下推论: 推论2对任意两个n阶树T1与T2.若Δ(T1) 综上可得同阶图的广义冠积的b-色数, 即如下推论: 推论3设G为n阶图,hn=(Hi)i∈{1,2,…,n}为n阶不相交图序列, 记max{Δ(Hi)|i=1,2,…,n}=Δ.若Δ 定理2设p,q是正整数.若p>q, 则φ(Kp∘Kq)=p; 若p≤q, 则φ(Kp∘Kq)=q+1. 定理3设G与H分别为p阶与q阶的图, 若Δ(H)+2≤p-1≤q+1, 则φ(G◇H)=p. 为度不增序列, 显然有 根据定理3知, 若n≥5且i≥-2, 则 φ(Cn◇Cn+i)=n;φ(Pn◇Pn+i)=n. 由Δ(Cn+i)=2及定理3, 有4≤n-1≤n+i+1, 因为n≥5, 显然不等式4≤n-1≤n+i+1成立, 即φ(Cn◇Cn+i)=n; 由Δ(Pn+i)=2及定理3, 有4≤n-1≤n+i+1, 因为n≥5, 显然不等式4≤n-1≤n+i+1成立, 即φ(Pn◇Pn+i)=n. 根据定理3, 可得满足定理3中约束条件的广义边冠积的b-色数. 推论4设G为p阶图,hp=(Hi)i∈{1,2,…,p}为q阶不相交图序列, 记max{Δ(Hi)|i=1,2,…,p}=Δ, 若Δ+2≤p-1≤q+1, 则G与hp的广义边冠积G◇hp的b-色数为p, 即φ(G◇hp)=p. 由定理3可得部分简单图的边冠积的b-色数, 但还存在某些简单图不满足定理3的约束条件, 如任意两个同阶图或完全图的边冠积的b-色数. 定理4设G与H都是n阶的简单图.若Δ(H) 根据定理4, 可推出特殊同阶图的广义边冠积的b-色数. 推论5设G为n阶图,hn=(Hi)i∈{1,2,…,n}为n阶不相交图序列, 记max{Δ(Hi)|i=1,2,…,n}=Δ.若Δ 定理5设p,q是正整数.若p>q+1, 则φ(Kp◇Kq)=p; 若p≤q+1, 则φ(Kp◇Kq)=q+2.
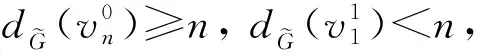
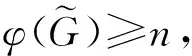
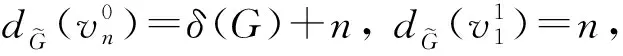
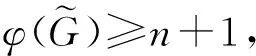


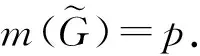

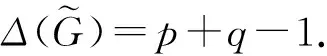
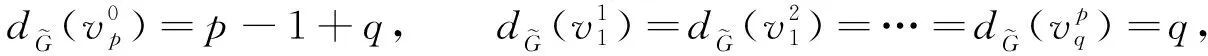

3 图的边冠积的b-染色