具有垂直传播传染病模型的动力学分析
2020-05-29李小平李辉来
李小平, 黄 蓉, 李辉来
(1.湘南学院 数学与金融学院, 湖南 郴州 423000; 2.天津师范大学 数学科学学院, 天津 300387;3.吉林大学 数学学院, 长春 130012)
0 引 言
传染病是危害人类健康的重要因素之一, 了解寄生虫与宿主的相互关系是了解寄生虫病发生、发展的基础, 也是人类防治寄生虫病的重要依据.文献[1-10]从不同角度研究了传染病模型的动力学行为, 这些研究对制定更有效的传染病预防控制策略具有重要意义.文献[3,5,11-14]的实验和观察研究表明, 寄生虫可降低宿主密度, 甚至可导致宿主种群灭绝.
文献[3]考虑了如下具有水平传播的微寄生虫数学模型:
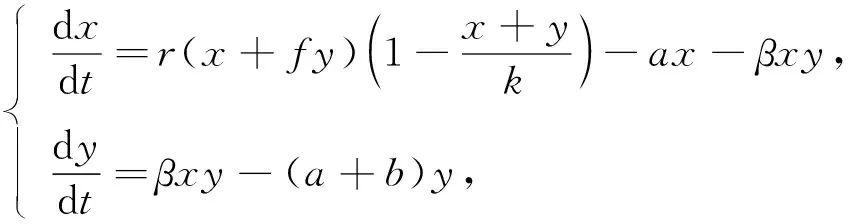
(1)
其中:x(t)和y(t)分别为t时刻未感染(易感)和受感染(染病者)宿主的密度;r为未感染宿主的平均增长率;f为受感染宿主的相对繁殖率;k为宿主群体的环境容纳量;a表示与寄生虫无关的宿主自然死亡率;b表示由寄生虫疾病引起的死亡率;β为感染的比例系数.模型(1)预测了受感染宿主和未受感染宿主稳定平衡的存在, 并预测种群以单调或者阻尼振荡的方式接近这种平衡.但该模型忽略了宿主免疫和恢复的可能性.
Ebert等[3]研究表明, 宿主种群密度随宿主繁殖率下降而下降, 并且预测具有垂直传播的寄生虫在降低宿主密度方面比只具有水平传播的寄生虫明显, 在繁殖力相同的情况下, 具有垂直传播的寄生虫更不易导致宿主灭绝.但文献[3]未对垂直传播的情形建立确定性模型.基于此, 本文通过假设受感染的宿主繁殖也遵循Logistic的生长规律对Ebert模型进行修正, 研究一种具有垂直传播的宿主-寄生虫传染病模型:

(2)
模型(2)中的参数都是非负的.在该模型中, 假设总宿主种群N由两个仓室组成: 一个是未感染的宿主类别, 用S表示; 另一个是寄生虫感染的宿主类别, 用I表示.因此,N=S+I.本文做如下假设:

2) 参数d1为与寄生虫无关的宿主自然死亡率;ε为由寄生虫引起的超额死亡率;β为寄生虫感染系数.
1 可行域和平衡点
首先, 将模型(2)的两个方程相加, 得

定理1假设di 定理2假设ω=r1d2-r2d1, 当下列条件至少有一个成立时: 则模型(2)有唯一的正平衡点E*=(S*,I*), 这里: 证明: 由模型(2)知其平衡点满足下列方程组: (3) 如果r1-r2+Mβ≠0, 则方程组(3)有唯一的解(S*,I*): (4) (5) 模型(2)的Jacobi矩阵为 (6) 可得点E0=(0,0)处的Jacobi矩阵为 由定理1的假设r1-d1>0,r2-d2>0知,E0=(0,0)是一个不稳定的点. 由式(6)可得点E1处的Jacobi矩阵为 (7) 同理可得 根据上述讨论可得: 定理3对于模型(2), 有如下结论: 1)E0是不稳定的平衡点; 模型(2)在正平衡点E*处的Jacobi矩阵为 则有 由Bendixson-Dulac理论可排除模型(2)存在极限环, 从而结论成立. 从而得基本再生数 (8) 定理6如果R0<1, 则E1是局部渐近稳定的; 如果R0>1, 则E1是不稳定的. 下面对模型(2)三个平衡点的稳定性进行数值模拟, 并给出相应的时间序列图, 相关数据列于表1. 表1 模型(2)的参数信息 图1 β=0.012时模型(2)的时间变化趋势Fig.1 Time variation trend of model (2) when β=0.012 图2 β=0.055时模型(2)的时间变化趋势Fig.2 Time variation trend of model (2) when β=0.055 图3 β=0.035时模型(2)的时间变化趋势Fig.3 Time variation trend of model (2) when β=0.035 1) Ebert等[3]研究忽略了宿主没有免疫和不可恢复, 考虑了一种具有水平传播的微寄生虫传播模型, 发现寄生虫可以降低宿主密度, 通过实验进一步发现宿主与寄生虫可能同时绝灭, 并认为具有垂直传播的寄生虫比水平传播的寄生虫更不易导致宿主灭绝.本文修正了Ebert等所建的数学模型, 假设受感染的宿主繁殖也遵循Logistic的生长规律, 研究了一类具有垂直传播的寄生虫传染病模型, 结果表明, 宿主-寄生虫关系存在4种可能性: 未感染的宿主和受感染的宿主同时灭绝; 未感染的宿主灭绝; 受感染的宿主灭绝; 未感染的宿主和受感染的宿主共存. 3) 通过数值模拟对所得结果进行了验证, 结果表明, 具有垂直传播的寄生虫可降低宿主的密度, 但不会导致宿主种群灭绝, 与文献[3]预测的结论一致.


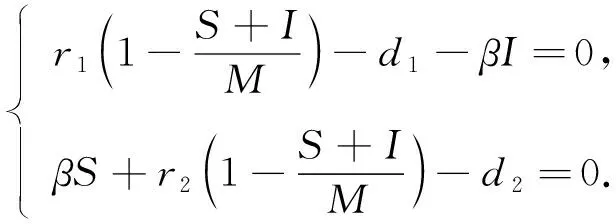



2 稳定性分析与基本再生数
2.1 3个平凡边界平衡点的稳定性



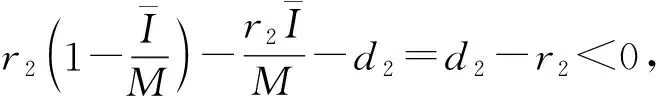


2.2 正平衡点E*的局部稳定性
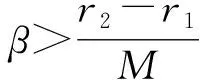

2.3 全局稳定性分析

2.4 基本再生数


3 数值模拟





4 结 论

