一类基于心理作用的SIRS传染病模型

李文轩, 李辉来, 赵彦军

(1.吉林大学 数学学院, 长春 130012; 2.东北师范大学人文学院, 长春 130117)

1 引言与引理

传染病是危及人类健康的一个重要因素, 利用微分方程理论建立数学模型研究传染病的传播过程和动力学行为已取得了很多结果[1-6].随着医学模式从生物医学向生物-心理-社会医学的转变, 心理作用在传染病治愈过程中的作用越来越明显.当易感者知道染病者感染后, 就会采取相应的预防控制措施, 从而影响发病率.一般人们心理作用(防控意识)的积极影响, 能将传染病的传播和流行控制在一定范围内, 再进行有效地治疗措施, 甚至能加快疾病的灭绝.文献[7-8]研究了易感人群心理作用下非线性发生率的SIS和SIR传染病模型, 获得了无病平衡点和地方病平衡点的全局渐近稳定性.

本文在文献[7-8]的基础上, 考虑人口增长满足Logistic方程, 在易感人群与感染人群心理作用的影响下, 建立基于心理作用和治疗的SIRS传染病模型：

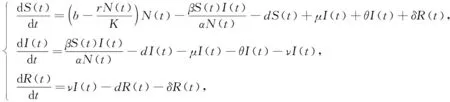
(1)

其中:S(t),I(t),R(t)分别表示t时刻易感者、感染者和免疫者的数量；N(t)=S(t)+I(t)+R(t)表示t时刻的人口总量；b为自然出生率；d为自然死亡率；r=b-d为内禀增长率；K为环境容纳量；β为传染率；α为心理作用系数(采取相应的预防控制措施影响发病率), 且假设1/K<α<1；μ为自然恢复率；θ为治愈率；ν为获得暂时免疫率；δ为丧失免疫率.所有参数均为正常数.

将模型(1)中3个方程相加有

可见总人口增长满足Logistic方程, 且S(t)=N(t)-I(t)-R(t).考虑模型(1)的等价模型:

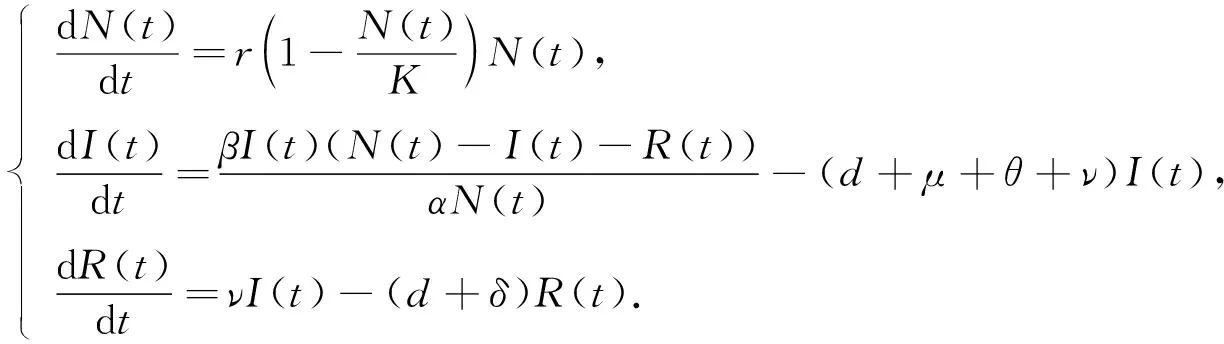
(2)

注意到N(t)≤K时,N′(t)≥0, 模型(2)是最终有界的.基于生物学意义, 本文仅在

G={(N(t),I(t),R(t))|N(t)≥0,I(t)≥0,R(t)≥0}

内讨论模型(2)的动力学性质.

定义基本再生数为

模型(2)的非负平衡点应满足如下方程组：

(3)

由方程组(3)可得:

引理1模型(2)在域G上存在边界平衡点O=(0,0,0)和无病平衡点E0=(K,0,0)； 当R0>1时, 还存在一个地方病平衡点E*=(K,I*,R*), 其中:

下面分析模型(2)非负平衡点的局部性态.

引理2模型(2)的边界平衡点O总是不稳定的； 当R0<1时, 模型(2)的无病平衡点E0是局部渐近稳定的; 当R0>1时, 模型(2)的无病平衡点E0是不稳定的； 当R0>1时, 模型(2)的地方病平衡点E*是局部渐近稳定的.

证明： 模型(2)在边界平衡点O处的Jacobi矩阵为

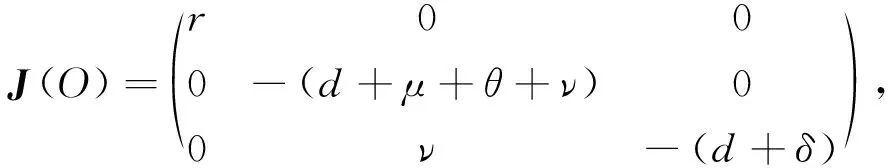
其特征值分别为：λ1=r>0,λ2=-(d+μ+θ+ν)<0,λ3=-(d+δ)<0.可知该点总是不稳定的.

模型(2)在无病平衡点E0处的Jacobi矩阵为

模型(2)在地方病平衡点E*处的Jacobi矩阵为

2 主要结果

定理1当R0≤1时, 模型(2)在G上的无病平衡点E0是全局渐近稳定的.

证明: 由引理1和引理2可知, 当R0<1时, 模型(2)的无病平衡点E0存在且为局部渐近稳定的.由引理3可知, 模型(2)第一个方程的平衡位置N=K是全局吸引的.于是, 由模型(2)可得极限系统：

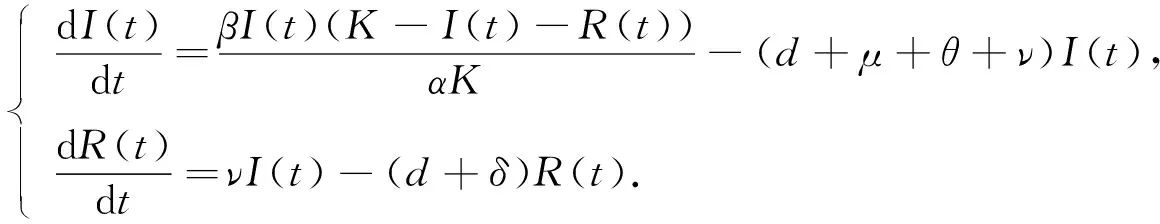
(4)

构造Lyapunov函数

当R0≤1时, 沿系统(4)的轨线计算V(t)的导数, 有

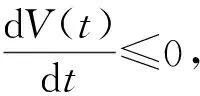
定理2当R0>1时, 模型(2)在G上的地方病平衡点E*是全局渐近稳定的.

证明： 由引理1和引理2可知, 当R0>1时, 模型(2)的地方病平衡点E*存在且为局部渐近稳定的.下面证明当R0>1时, 地方病平衡点E*是全局渐近稳定的.

由引理3和定理1可知, 模型(2)在平衡位置N=K是全局吸引的, 且得出极限系统(4).当R0>1时, 极限系统(4)存在一个正平衡位置I=I*与R=R*.下面将极限系统(4)改写为如下等价系统:

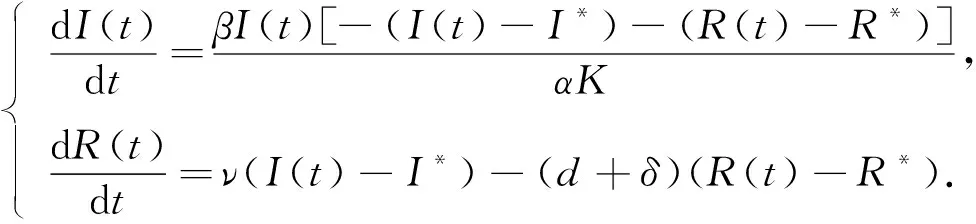
(5)

构造Lyapunov函数

沿系统(5)的轨线计算V(t)的导数, 有

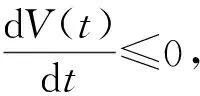
3 数值模拟

首先, 应用MATLAB对模型(2)进行数值模拟, 以验证结论的正确性.基于文献[10]的参数估计, 在模型(2)中取b=0.5,d=0.2,α=0.1,K=500,β=0.05,μ=0.05,θ=0.2,ν=0.1,δ=0.01, 满足条件R0≤1.由定理1知, 无病平衡点E0是全局渐近稳定的.在模型(2)中取b=0.5,d=0.2,K=500,β=0.2,α=0.1,μ=0.05,θ=0.2,ν=0.1,δ=0.01, 满足条件R0>1.由定理2知, 地方病平衡点E*是全局渐近稳定的.模拟结果分别如图1和图2所示.

图1 无病平衡点的全局渐近稳定性Fig.1 Global asymptotic stability of disease-free equilibrium point

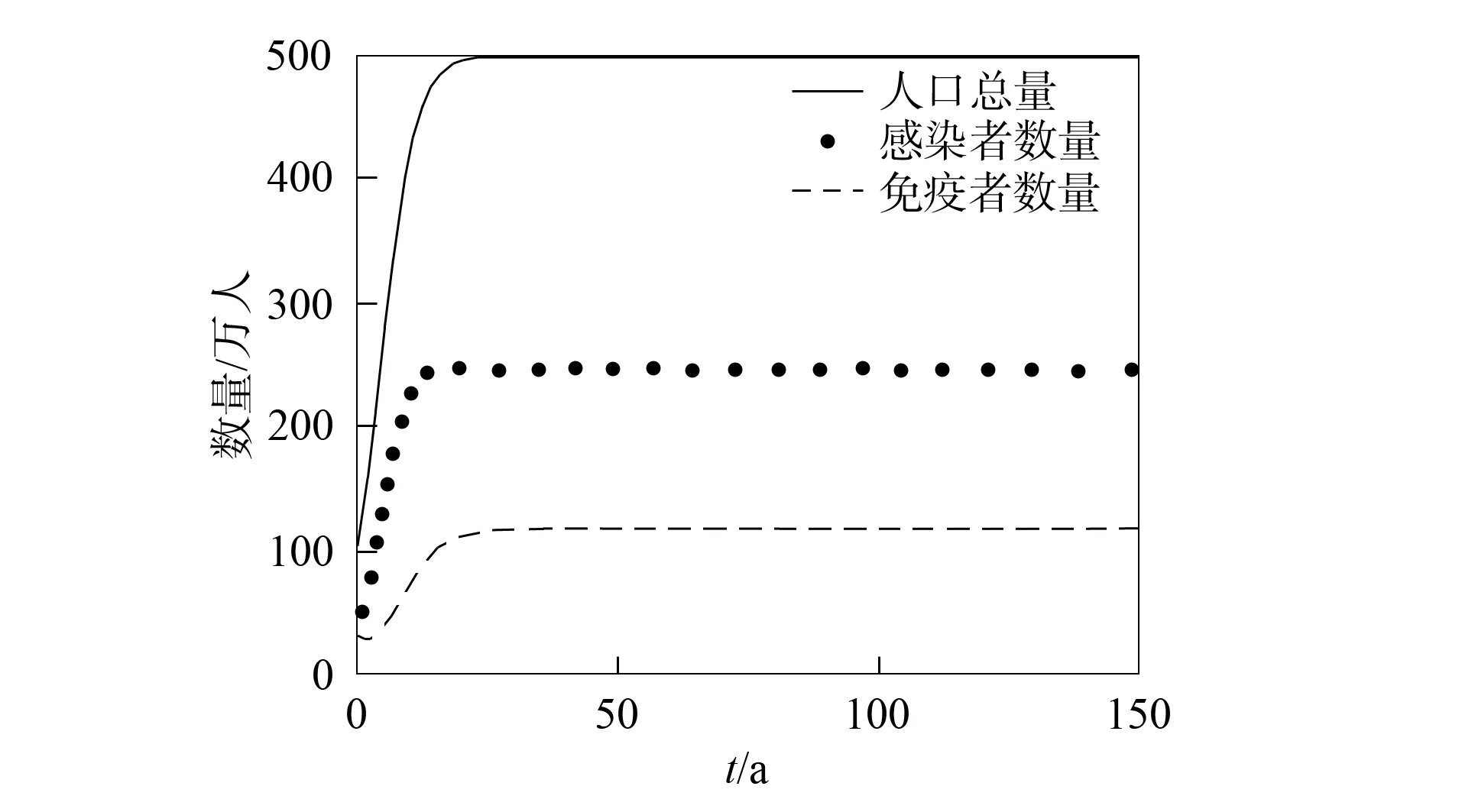
图2 地方病平衡点的全局渐近稳定性Fig.2 Global asymptotic stability of endemic equilibrium point

其次, 应用MATLAB对模型(2)中心理作用系数α进行数值模拟.利用图1中无病平衡点和图2中地方病平衡点的数据, 对α取从0.2～1、步长为0.2的5组数据进行数值模拟, 结果分别如图3和图4所示.由图3和图4可见, 心理作用系数越大, 地方病平衡点中感染者的数量I*越小, 即积极的心理作用可将传染病控制在小范围内, 甚至达到疾病灭绝.

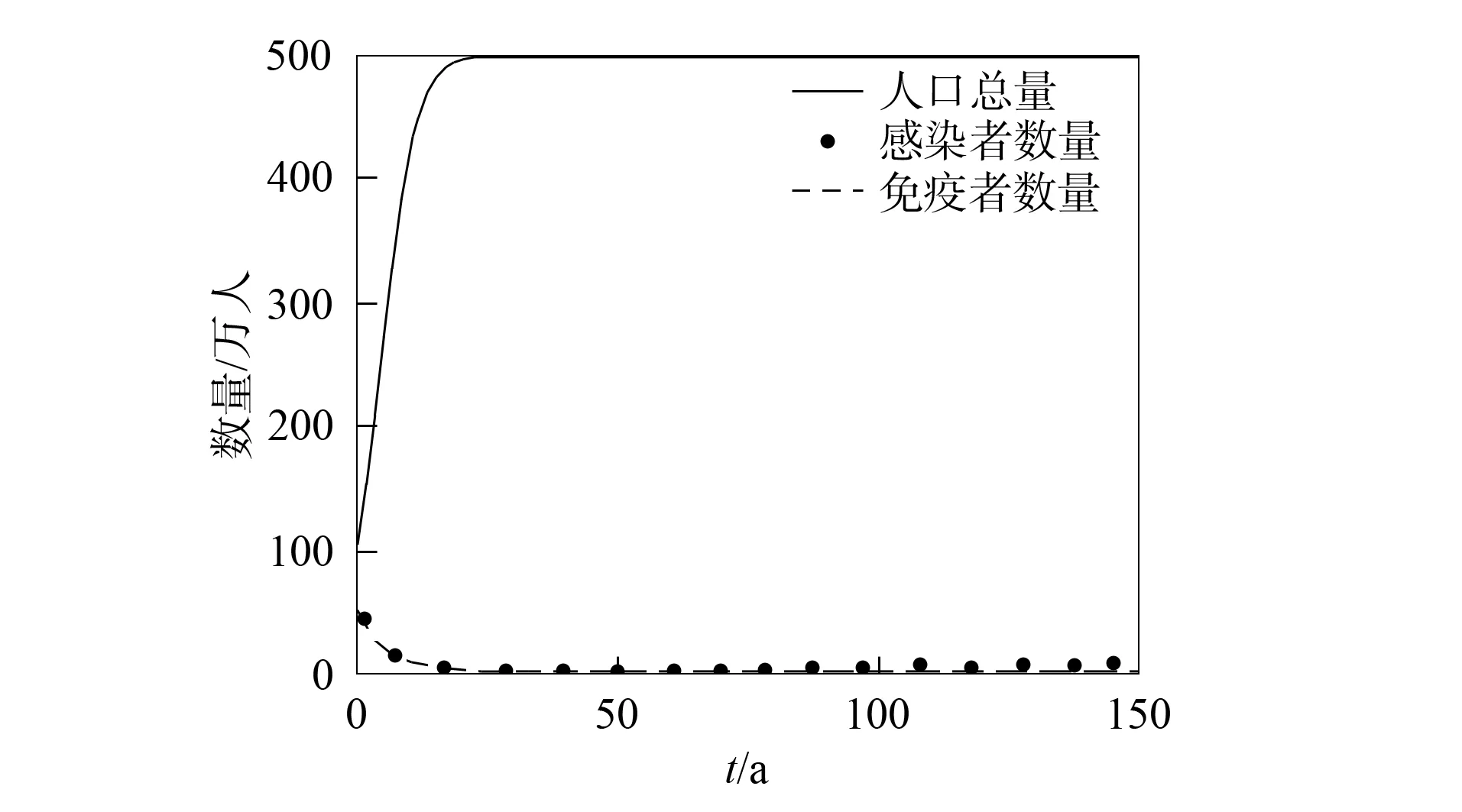
图3 无病平衡点随心理系数变化曲线Fig.3 Curves of disease-free equilibrium point with psychology coefficient

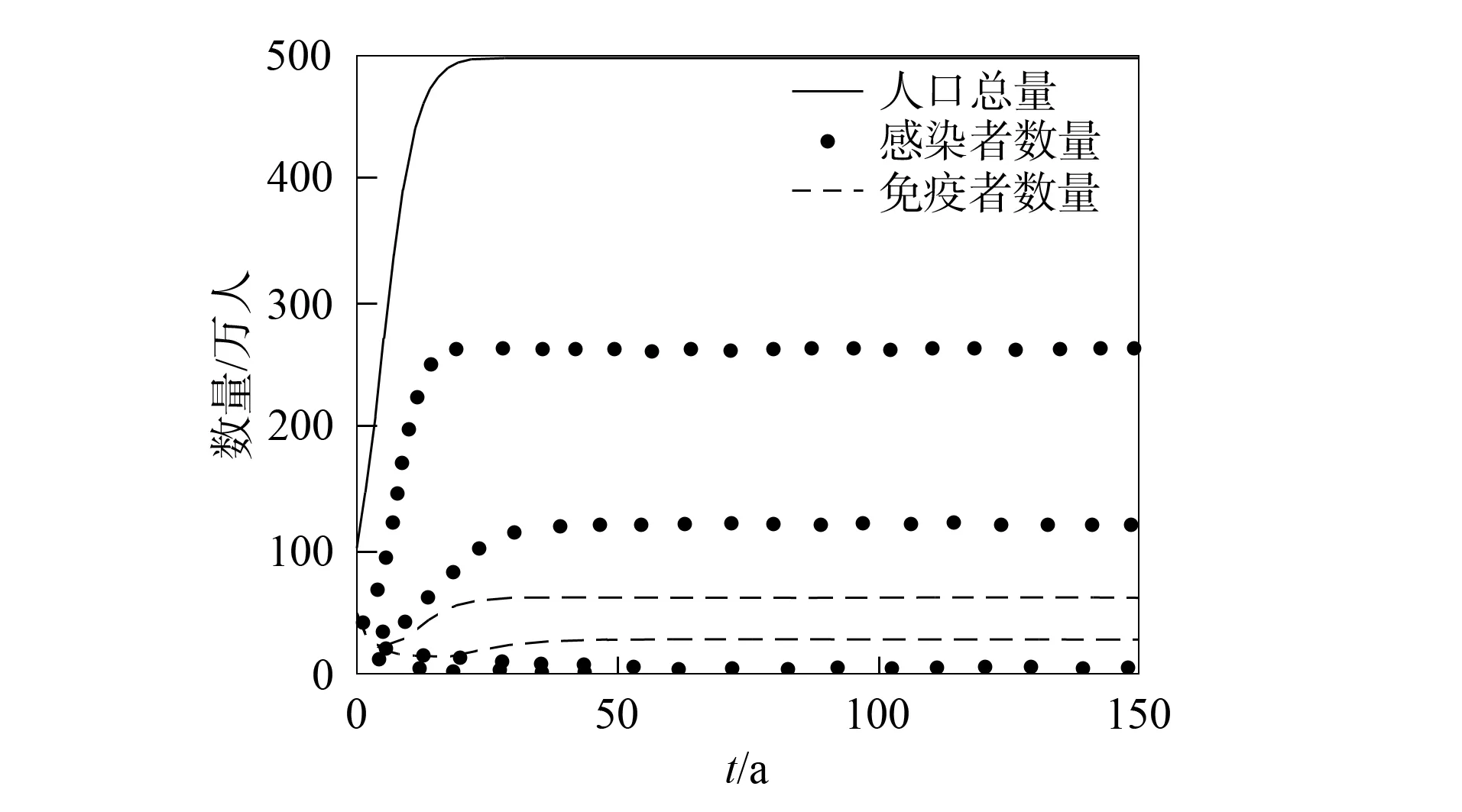
图4 地方病平衡点随心理系数变化曲线Fig.4 Curves of endemic disease equilibrium point with psychology coefficient

综上, 由定理1知, 当基本再生数≤1时, 疾病将在该系统中灭绝, 表明提高人们对传染病的防控意识并积极采取治疗措施, 可有效控制传染病的传播, 进而彻底根除传染病.由定理2知, 当基本再生数>1时, 疾病将在该系统中持续, 表明当人们对传染病的防控意识较弱、治疗措施相对滞后时, 可导致传染病持续流行, 易感者人群和感染人群将渐近稳定在一组定值上.由数值模拟结果可知, 人们心理作用的积极影响， 能将传染病的传播和流行控制在一定范围内, 在此基础上再进行有效地治疗措施, 可加快传染病的灭绝.