常规岛建(构)筑物60年设计基准期荷载分项系数研究
2020-05-29章骏华林少波干梦军张建成
章骏华,林少波,陈 飞,干梦军,张建成,徐 勍,李 萍,吕 平
(华东电力设计院有限公司,上海 200063)
三门核电一期工程采用目前国际上技术最为先进的两台AP1000核电机组,规定核电厂的使用寿命为60年,这就要求核电厂的设计使用年限不小于60年,进而确定建(构)筑物设计基准期为60年、而目前我国规范体系的设计基准期为50年,设计使用年限仅考虑了几种特殊情况,比如5年、50年、100年等。以上分析表明,规范中的分项系数已不能满足三门核电一期工程的设计要求,本项研究的目的即是针对三门核电一期工程的实际情况,计算与之对应的分项系数,最终使本项工程的建(构)筑物在规定的设计使用年限内满足《建筑结构可靠度设计统一标准》GB 50068—2001中规定的可靠指标要求。
目前,我国规范的编制采用以概率理论为基础的极限状态设计法,以可靠指标度量结构构件的可靠度,采用分项系数的设计表达式进行设计。本文采用了与规范相同的技术路线,但是考虑了三门核电一期工程建(构)筑物的结构特殊性,对目标可靠指标、可变荷载统计参数、可变荷载分项系数等进行了重新计算,从而符合三门核电一期工程的实际设计情况。
当然,基于可靠度的概率极限状态设计方法十分繁琐、复杂,现将主要的研究内容简介如下:
(1)目标可靠指标的选取,采用了目前较为认可的“校准法”,即通过可靠度理论对现行规范的反演计算,得到目前规范隐含的可靠度水平,最终确定目标可靠指标。
(2)根据已有的荷载统计参数,计算60年设计基准期、60年设计使用年限下的荷载统计参数。
(3)假定抗力、恒载等因素不随时间变化(这是符合规范与实际情况的),通过调整可变荷载分项系数,使三门核电一期工程建(构)筑物达到预定的可靠度水平。
总之,本项研究既保证了与现有规范的衔接,又满足了三门核电一期工程实际的特殊要求,有利于工程应用。
1 极限状态设计表达式
我国规范将极限状态可分为两类:(1)承载能力极限状态:这种极限状态对应于结构或结构构件达到最大承载能力或不适于继续承载的变形;(2)正常使用极限状态。这种极限状态对应于结构或结构构件达到正常使用或耐久性能的某项规定限值。
对于承载能力极限状态,规范要求采用荷载效应的基本组合和偶然组合进行设计。对于基本组合的极限状态设计表达式为:
(1)
(1)由可变荷载效应控制的组合:
(2)
(2)由永久荷载效应控制的组合:
(3)
式中:γG= 1.2;
γQ= 1.4;
SGk,SQk,Rk分别为50年基准期下的恒载、可变荷载效应标准值和抗力标准值。
对于偶然组合,荷载效应组合的设计值宜按下列规定确定:偶然荷载的代表值不乘分项系数;与偶然荷载同时出现的其他荷载可根据观测资料和工程经验采用适当的代表值。
对于正常使用极限状态,应根据不同的设计要求,采用荷载的标准组合、频遇组合或准永久组合,并应按下列设计表达式进行设计:
S≤C
(4)
式中:C——结构或结构构件达到正常使用要求的规定限值。
对于标准组合,荷载效应组合的设计值S应按下式采用:
(5)
对于频遇组合,荷载效应组合的设计值S应按下式采用:
(6)
对于准永久组合,荷载效应组合的设计值S可按下式采用:
(7)
采用60年基准期时,承载能力极限状态下,荷载效应基本组合中的分项系数需根据60年基准期进行调整,此时极限状态设计值表达式为:
(8)
(1)由可变荷载效应控制的组合:
(9)
(2)由永久荷载效应控制的组合:
(10)
式中:γo= 1.0;
γG= 1.2;
根据可靠度理论计算可变荷载分项系数γQ、SGk,60、SQk,60、Rk,60分别为60年基准期下的恒载、可变荷载和抗力标准值。
2 校核规范中的可靠指标
2.1 校核方法简介
结构的可靠度是指结构在规定的时间内,在规定的条件下,完成预定功能的概率,可以用失效概率Pf来描述。如果各设计基本变量的理论(真实)概率分布为已知,则可以根据概率的知识求解出失效概率(见图1)。但在实际工程很难精确掌握各设计基本变量的理论分布,且变量有多个时要进行多重积分存在一定的问题。目前在实用上使用简化的方法来衡量可靠度。通常利用分布数字的特征——一阶原点矩(均值)和二阶中心矩(方差)近似描述随机变量的分布特性,以可靠指标β来表达结构的失效概率。
可靠指标的物理意义:若随机变量服从正态分布,β的物理意义是从μz到原点以标准差σz为量测单位的距离(见图1)。可靠指标只与功能函数的均值和标准差有关。
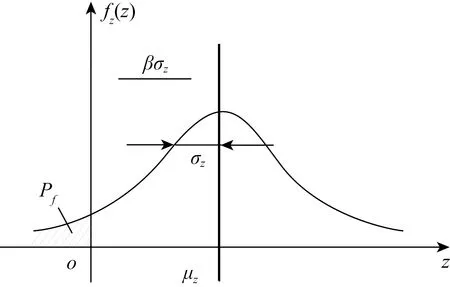
图1 结构构件可靠指标与失效概率的关系Fig.1 Relationship between reliability index & failure probability of structural components
可靠指标的计算方法选择:
计算可靠指标的最典型的两种方法:
(1)中心点法——不考虑基本变量的实际分布,直接假定其服从正态或对数正态分布,导出结构可靠度分析的表达式。由于在分析时采用了泰勒级数在均值(中心点)展开,故简称为中心点法。
(2)验算点法——考虑基本变量的实际分布类型,把非正态分布随机变量等效化成正态变量,计算可靠指标。由于计算的是设计验算点的β值,故称为验算点法。《建筑结构概率极限状态设计》(中国建筑工业出版社,1990)第160页中有这样一段话:“由西德的拉克维茨(Rackwitz,R.)和菲斯勒(Fiessler,B.)提出的方法,它经系统改进后作为结构安全度联合委员会(J.C.S.S.)的文件(结构统一标准规范的国际体系第一卷)附录推荐给土木工程界。这个方法也被很多国家所采纳,我国的《建筑结构可靠度设计统一标准》GB 50068—2001也是以该方法作为可靠性校准的基础。”引文中的“方法”就是验算点法。
本项研究采用验算点法,对我国现有规范进行可靠度校核。
目标可靠指标的确定方法通常有三种:①事故类比法;②经济优化法;③经验校准法。确定目标可靠指标不仅要考虑理论结果,还要考虑工程设计的现实情况,保证与规范的衔接,以免因为材料用量的过大波动而引起设计人员的不安。在实际应用中,前两种方法比较困难,规范中对于其目标可靠指标的确定主要采用经验校准法。本项研究也采取此方法,通过对现行设计规范安全度的校核,利用反演计算,核实出按现有规范设计在结构中隐含的相应可靠指标值,然后分析、调整,最终得到合理的目标可靠指标。
具体校核过程如下:
恒载加一种可变荷载的设计表达式为:
(11)
将公式(11)转化为用均值表示:
(12)
则:
(13)
而荷载效应比ρ=SQk/SGk、结构重要性系数、各分项系数γ0、γG、γQ、γR各变量的均值系数和变异系数δR、χR、δSG、χSG、δSQ、χSQ都可以查中华人民共和国国家标准《建筑结构设计统一标准》(GBJ 68—84)。
荷载效应的均值、标准差可以由荷载统计参数推算出,抗力的均值、标准差由公式(13)可进一步得到。通过一次二阶矩理论,对三种随机变量进行当量正态化处理,最后根据MATLAB程序得出现行规范分项系数表达式所对应的钢结构、混凝土构件的可靠指标。
2.2 校核结果
验算点法校核可靠指标。
根据公式(11)中给出的极限状态方程,各分项系数取值如表1所示。
本文分别对钢结构偏心受压构件、钢结构轴心受压构件、混凝土结构构件进行了可靠指标的校核,校核结果如表2和表3所示。
50年设计基准期下混凝土延性结构可靠指标如表4所示, 50年设计基准期下混凝土脆性结构可靠指标如表5所示。

表1 校核规范可靠指标所用分项系数取值
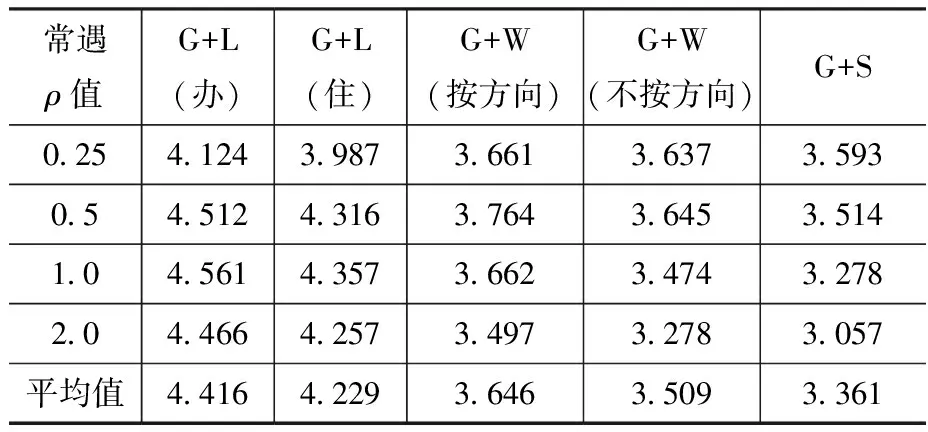
表2 现行规范钢结构偏心受压构件可靠指标

表3 现行规范钢结构轴心受压构件可靠指标
注:以上两表中的常用荷载效应比均与中华人民共和国国家标准相同;荷载简单组合比中华人民共和国国家标准增加了G(恒载)+W(风载)(不按方向)和G(恒载)+S(雪载)两种情况。

表4 50年设计基准期下混凝土延性结构可靠指标

表5 50年设计基准期下混凝土脆性结构可靠指标
2.3 目标可靠指标取值
根据表2和表3中的计算结果,通过最小二乘法求出最佳的可靠指标为3.93,故建议取目标可靠指标为4.0。
根据表4和表5,对于混凝土结构延性结构,目标可靠指标取为4.0;对于混凝土结构脆性结构目标可靠指标取为4.3。
3 计算60年设计基准期的荷载统计参数
3.1 荷载统计参数修正总原则
在保证60年设计基准期下的荷载保证率与中华人民共和国国家标准GB 50009—2001 《建筑结构荷载规范》50年设计基准期相同的情况下,随着设计基准期的变化,则荷载标准值、荷载分布的参数(均值、方差)等会发生变化,那么,荷载的均值系数、变异系数必然也跟着发生变化。当使用可靠度理论计算分项系数时,需要在已有荷载统计参数的基础上调整得到60年荷载统计参数,本文中引用的荷载统计参数源于中华人民共和国国家标准 《建筑结构设计统一标准》(GBJ 68—84)。
既然是基于中华人民共和国国家标准《建筑结构设计统一标准》(GBJ 68—84)的荷载统计参数,保证与中华人民共和国国家标准《建筑结构荷载规范》(GB 50009—2001)相同的荷载保证率计算60年设计基准期的荷载统计参数,那么就有必要对比分析两本规范与60年设计基准期荷载设置水平的区别:
(1)中华人民共和国国家标准《建筑结构设计统一标准》(GBJ 68—84)、中华人民共和国国家标准《建筑结构荷载规范》(GB 50009—2001)采用的设计基准期为50年,而本项研究的设计基准期为60年;
(2)中华人民共和国国家标准《建筑结构设计统一标准》(GBJ 68—84)采用的楼面荷载的标准值为 ,风、雪荷载的重现期为30年一遇;中华人民共和国国家标准《建筑结构荷载规范》(GB 50009—2001)采用的楼面荷载的标准值为 ,风、雪荷载的重现期为50年一遇;为了保证60年设计基准期下的荷载保证率与中华人民共和国国家标准《建筑结构荷载规范》(GB 50009—2001)50年设计基准期相同,则各类荷载标准值必有所提高。
3.2 计算60年基准期下荷载统计参数
可变荷载是指在设计基准期内其量值随时间变化,且其变化与平均值相比不可忽略不计的荷载。显然,可变作用的统计规律是与时间有关的。规范中是将可变荷载化为平稳二项随机过程{Q(t) ,t∈[0,T]},假定将荷载随机过程的样本函数化为等时段(每一时段长为τ)的矩形波函数,任一时段上荷载的分布函数就是任意时点荷载分布函数,且在不同时段上其概率分布相同,令为FQτ(x)。不同时段上荷载的作用是相互独立的。则设计基准期T可化为r(r=T/τ)个等时段,每一时段上荷载出现的概率为p,不出现的概率为1-p。
本文主要研究了建筑工程中常用的一些可变荷载,比如楼面活荷载、风荷载(按风向、不按风向)、雪荷载,计算它们在60年设计基准期下荷载标准取值。
根据大量的统计分析,一般假定以上几种可变荷载均服从极值Ⅰ型分布:
F(x)=exp{-exp[-α(x-u)]}
(14)
u=μ-0.577 2/α
(15)
(16)
(1)楼面活荷载
楼面活荷载可分为楼面持久性荷载(Li)和楼面临时性荷载(Lr)两类,调查表明两者的任意时点的时段均取τ=10年。 《建筑结构设计统一标准》GBJ 68—84的设计基准期为50年,楼面活荷载的标准值为1.5 kN/m2,则住宅楼面活荷载、办公楼楼面活荷载的保证率分别为79.8%和92.1%;而《建筑结构荷载规范》GB 50009—2001中规定将楼面荷载的标准值提高为2 kN/m2,实际上是将荷载保证率提高了,提高后的住宅楼面活荷载、办公楼楼面活荷载的保证率分别为97.4%和99.0%。本文即是在住宅楼面活荷载、办公楼楼面活荷载的保证率分别为97.4%和99.0%荷载设置水平(与现行规范相同)下计算60年基准期下的楼面荷载取值标准。
荷载标准值与设计基准期T内的保证率有这样的关系:
pk=FL(LkT)=exp{-exp[-α(LkT-β)]}
(17)
所以:
(18)
进一步简化为:
(19)
故楼面活荷载标准值与其均值、方差有如下关系。
办公楼荷载:
LkT=μLT+3.14σLT
(20)
住宅楼荷载:
LkT=μLT+2.39σLT
(21)
(22)
σLT=σL
(23)
式中:LkT——设计基准期T对应的楼面荷载标准值;
μLT,σLT——分别为设计基准期T内的均值和标准差;
μL,σL——分别为任意时点的均值和标准差;
m——设计基准期T内荷载平均变动次数。
从表6、表7中可以看出, 60年基准期下的楼面荷载标准值比50年基准期下的荷载标准值大约提高了2%左右。
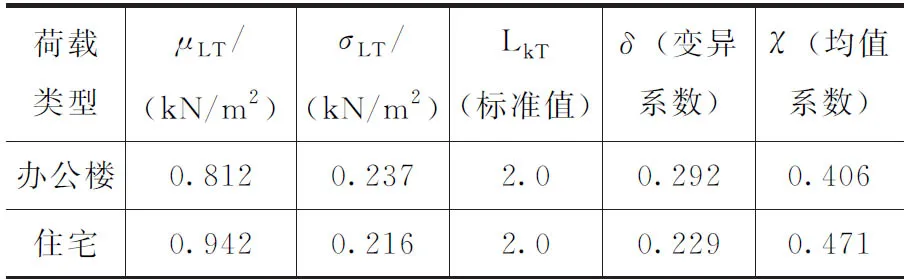
表6 50年设计基准期下楼面荷载统计参数

表7 60年设计基准期下楼面荷载统计参数
注:办公楼楼面荷载标准值实际为2.03 kN/m2,为统一起见,取2.04 kN/m2,偏安全。
(2) 风、雪荷载
根据设计基准期50年内发生超越荷载设计值的概率与60年设计基准期内发生荷载超越设计值的概率一致,即:
FQ,50(Q50,k)=FQ,60(Q60,k)
(24)
式中:FQ,50(),FQ,60(·)——分别为50年、60年设计基准期下风荷载最大值概率分布函数;
Q50,k,Q60,k——分别为50年、60年设计基准期下风荷载的标准值。
计算表明,60年基准期下的风、雪荷载重现期为60年。
与重现期对应的风、雪荷载标准值为:
pk=FQ(Qk)=exp{-exp[-α(Qk-β)]}
(25)
(26)
(27)
式中:μQ,σQ——分别为风荷载年最大值概率分布的均值与标准差;
FQ(·)——风荷载年最大值分布函数;
Qk——风荷载标准值;
Tr——重现期,即Tr年一遇。
根据公式(26)和公式(27)的计算,结论是风荷载的标准值增加了约3%,雪荷载的标准值增加了约4%,具体的修正后的荷载统计参数如表8所示。
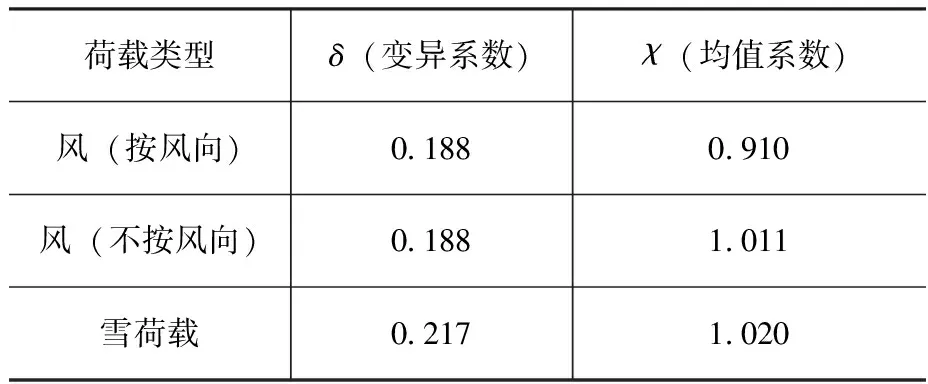
表8 60年基准期下风荷载统计参数
4 根据可靠度理论确定分项系数
4.1 技术路线
本项研究,拟通过调整可变荷载的分项系数使60年设计基准期的三门核电一期工程满足一定目标可靠指标的要求。也就是说,考虑结构重要性系数不变;抗力、恒载分项系数不变,抗力、恒载不随时间变化,其统计参数不随设计基准期的变化而变化。
表9给出了该问题的直观描述,表10为本文采用的抗力统计参数。
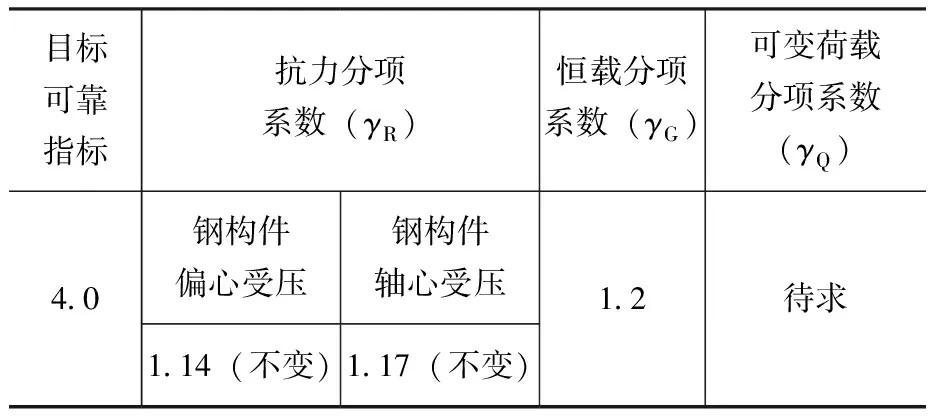
表9 60年设计基准期计算分项系数的直观描述
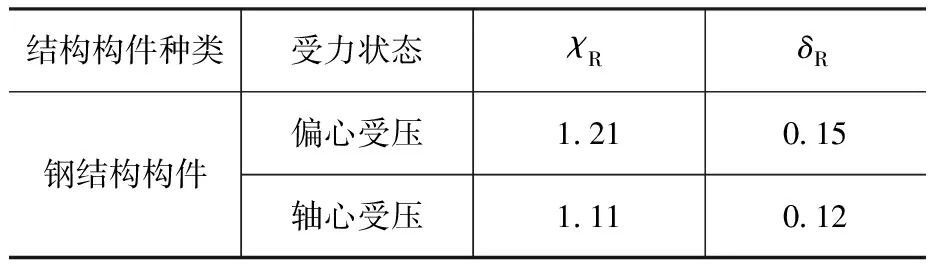
表10 抗力统计参数
4.2 理论说明
结构在设计使用年限T内的功能函数表示如下:
ZT=R-SG-SQT
(28)
设基本变量R、SG、SQT是相互独立的随机变量,其中随机变量R(抗力)服从对数正态分布,随机变量SG(恒载效应)服从正态分布,随机变量SQT(可变荷载效应)服从极值I型分布。
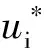
(29)
(30)

抗力在设计验算点处当量正态变换后的参数为:
(31)
(32)
恒载效应在设计验算点处当量正态变换后的参数不变:
σ′SG=σSG
(33)
μ′SG=μSG
(34)
可变荷载效应在设计验算点处当量正态变换后的参数为:
(35)
(36)
对于功能函数公式(28)、公式(30)可简化为:
(37)
然后依次代入公式(31)、公式(33)、公式(36)中的参数σ′R、σ′SG、σ′SQT,可以分别求出αR、αSG、αSQT。
可以看出由初始的设计验算点可以推出与此相对应的各变量的方向余弦,再根据公式(29)和已知的可靠指标,显然可以推出新的设计验算点。我们知道在设计验算点处满足这样的条件:
(38)
观察公式(38),建立这样的迭代格式:
(39)
(40)
将公式(38)转化为实用设计表达式:
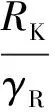
(41)
(42)
最终推出γQ为:
(43)
4.3 60年基准期可变荷载分项系数取值
根据以上理论推导,通过自编的MATLAB程序计算分析得出可变荷载分项系数,如表11和表12所示。
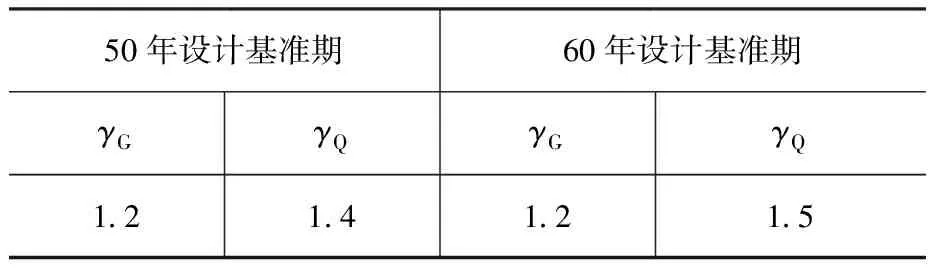
表11 由可变荷载效应控制的组合
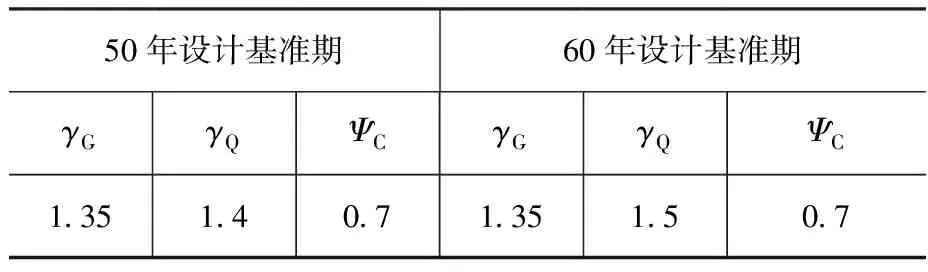
表12 由恒载效应控制的组合
5 结论
综上所述,三门核电一期工程常规岛建(构)筑物60年基准期下的荷载分项系数取值是能满足工程设计需要,使本工程建(构)筑物达到预定的可靠度水平。
