Fe- Mn- X(X=Al,Si)三元系合金扩散行为的试验与计算研究

李佳媛 郑伟森 鲁晓刚,2

(1.上海大学材料科学与工程学院，上海 200444; 2.上海大学材料基因组工程研究院，上海 200444)

随着汽车越来越成为生活必需品，环境污染和原料短缺问题日趋严重，迫使各国政府不得不寻求各种节能减排的措施。汽车尾气排放量及油耗都与车重呈线性关系[1]。因此，开发轻质高强钢实现汽车轻量化已经成为汽车行业的必然趋势。轻质高强钢中常见合金元素有Mn、Al、Si等。根据合金成分和热处理工艺，轻质钢基体大致可分为奥氏体(FCC)、铁素体(BCC)以及奥氏体- 铁素体双相3种。因此，研究合金元素在关键三元系Fe- Mn- X(Al, Si)奥氏体和铁素体中的扩散行为对预测轻质高强钢的组织演变至关重要。Zheng等[2- 3]采用扩散偶方法先后对BCC结构Fe- Mn- Al和FCC结构Fe- Mn- Si三元合金的扩散动力学进行了研究，获得了可靠的原子移动性参数。然而，至今仍缺少关于FCC结构Fe- Mn- Al和BCC结构Fe- Mn- Si三元系完善的扩散动力学描述。

本文采用扩散偶方法测定了Fe- Mn- Al三元系FCC相的成分- 距离曲线，采用二元外推的方法获得了三元动力学数据库，并与试验数据进行对比验证了所建数据库的可靠性。同时，通过评估Fe- Mn- Si三元系BCC相的扩散试验数据，对Fe- Mn- Si三元系进行了动力学优化。

1 原子移动性模型

原子移动性模型是Anderson和Ågren[4]基于绝对反应速率理论提出的，组元i的原子移动性参数可以表示为：

(1)

(2)

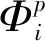
互扩散系数可表示为：

(3)

式中：μi表示组元i的化学势，可通过热力学数据库计算得到。δip是Kronecher算符，当i=p时，δip为1，其他情况下为0。

2 试验材料与过程

对于Fe- Mn- Al三元系，试验原料为纯铁(99.99%，质量分数，下同)、纯锰(99.95%)和纯铝(99.999%)。采用WK- Ⅱ型非自耗真空电弧炉熔炼合金，将熔炼好的纽扣锭封入充有氩气保护气氛的石英管中，用Carbolite管式炉加热至1 373 K均匀化退火7天，再将纽扣锭线切割成5 mm×5 mm×5 mm的块状试样。

将块状试样打磨、抛光后，使用ZC- ZK/WY3型扩散设备，通过加压，维持2%形变量，在1 173 K保温1 h后，块状试样形成扩散偶，封石英管后置于Carbolite管式炉中进行扩散退火，扩散偶成分及热处理条件见表1。最后采用电子探针对扩散偶界面进行微区成分分析。

表1 Fe- Al- Mn三元系扩散偶的化学成分及热处理工艺Table 1 Chemical compositions and heat treatment process of diffusion couples for the Fe- Mn- Al ternary system

3 结果与讨论

3.1 Fe- Mn- Al三元系

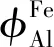
通过合理外推获得了Fe- Mn- Al三元系FCC相的动力学数据库，相关原子移动性参数如表2所示。

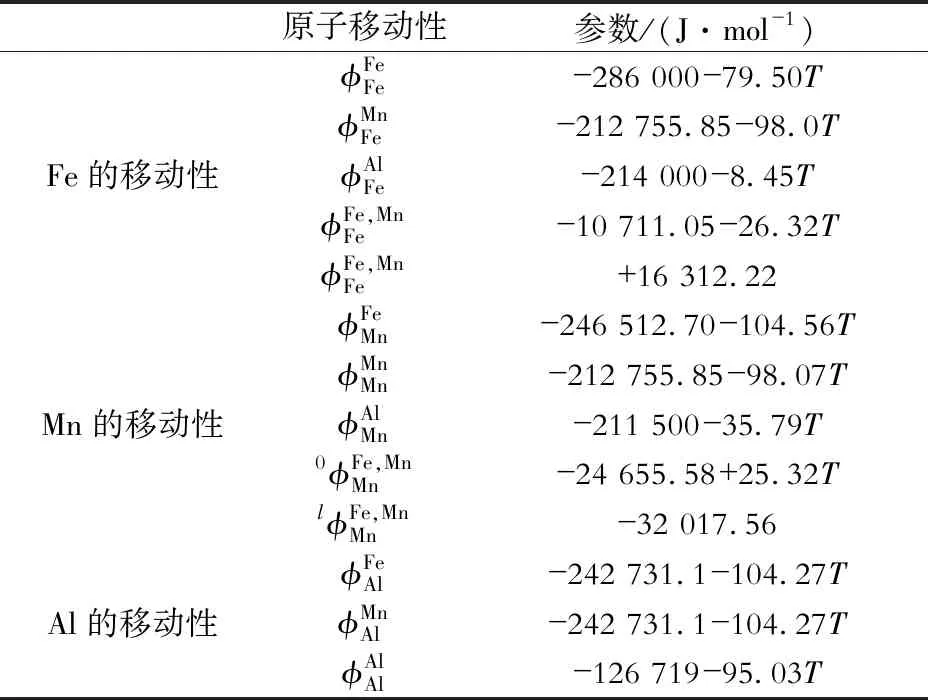
表2 Fe- Mn- Al三元系FCC相的原子移动性参数汇总Table 2 Summary of atomic diffusion mobilities in FCC phase Fe- Mn- Al ternary system

采用合理外推获得的动力学描述，计算不同试验条件下的成分距离曲线和扩散通道，并与试验测定结果进行比较。图1和图2分别为模拟预测的Fe- Mn- Al三元合金扩散偶的成分- 距离曲线和扩散通道与试验数据的比较。由图可见，两者的计算结果与试验数据均吻合较好。但图1中试验测定的Mn元素成分分布均表现出了一定的波动性，这是由于Mn与Al的原子序数相差较大而在电子探针检测中引起的荧光(激光)效应导致的[9]。

由于Al是铁素体形成元素，在Fe- Mn- Al合金FCC相中的溶解度较低，所以通过外推得到的三元动力学数据库可以很好地描述Fe- Mn- Al体系FCC相的扩散行为，不需要再引入额外的交互作用参数。

3.2 Fe- Mn- Si三元系

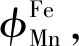
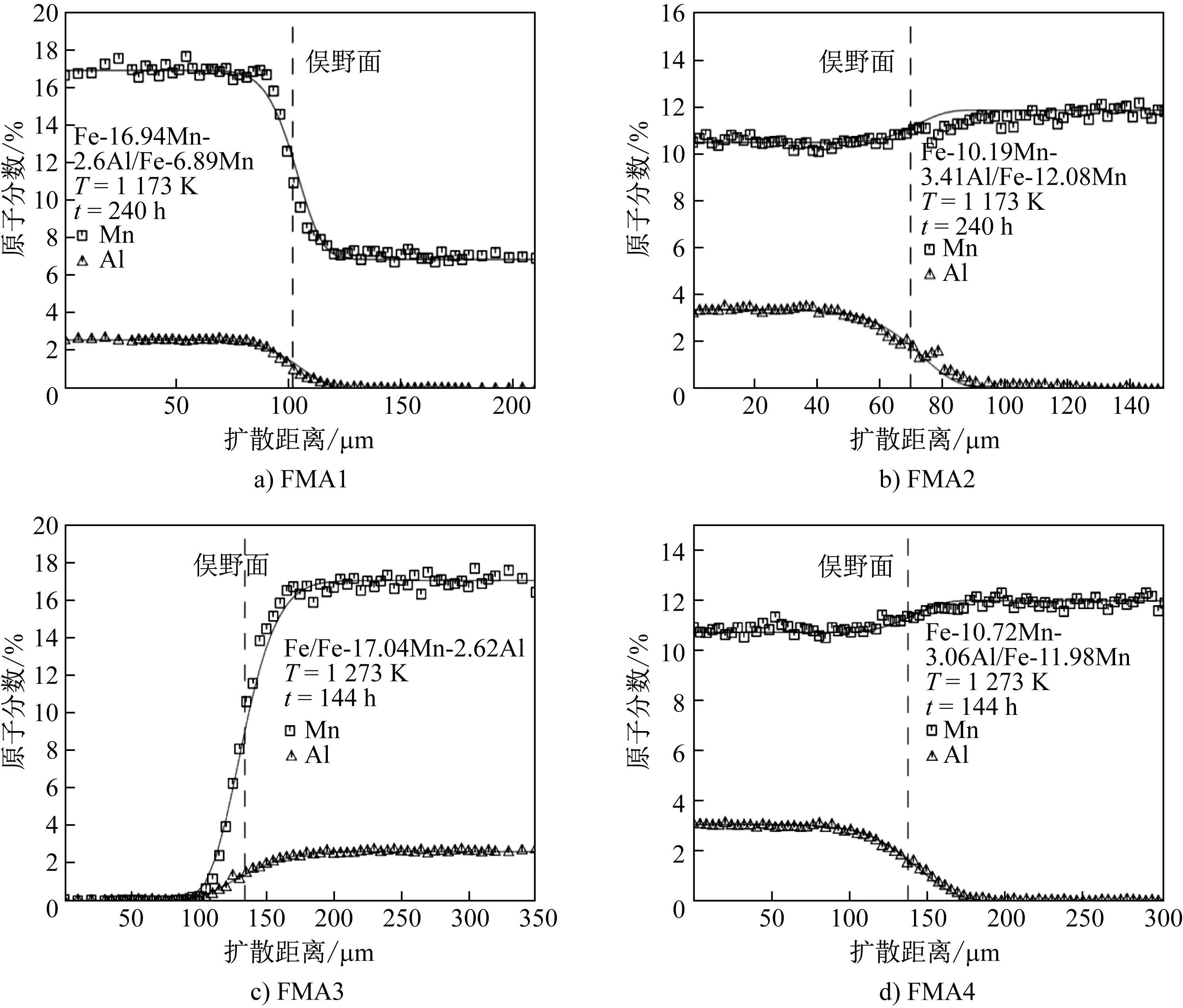
图1 模拟计算的Fe- Al- Mn扩散偶成分距离曲线与试验数据的比较Fig.1 Comparison between the simulated and experimental concentration profiles of Fe- Mn- Al diffusion couples

图2 模拟计算的Fe- Al- Mn扩散偶的扩散通道与试验数据的比较Fig.2 Comparison between the simulated and experimental diffusion paths of Fe- Mn- Al diffusion couples

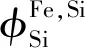
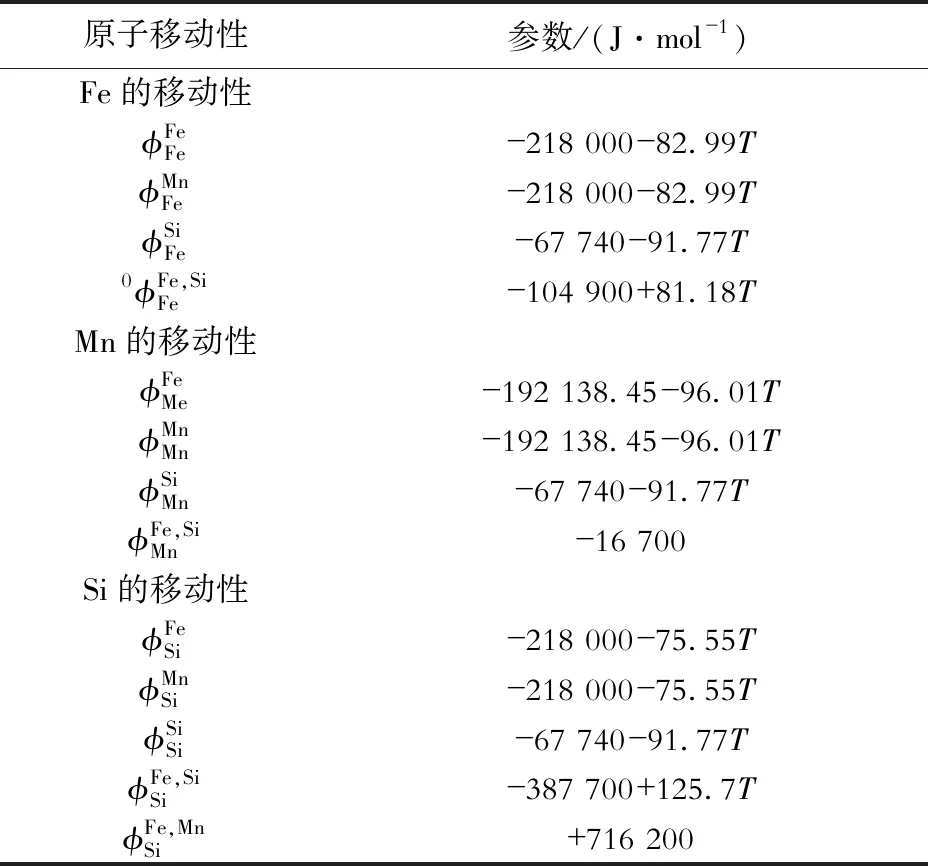
表3 Fe- Mn- Si三元系BCC相的原子移动性参数汇总Table 3 Summary of atomic diffusion mobilities in BCC phase Fe- Mn- Si ternary system

图3为采用本文优化的原子移动性参数计算得到的Fe- Mn- Si系BCC相的主扩散系数，并与朱小和等[12]的试验结果进行比较，其中虚线部分表示主扩散系数乘以因子2或0.5的结果，虚线范围内是扩散系数测量可以接受的误差范围，可见采用优化的数据库对互扩散系数的预测误差在扩散系数的0.5～2倍之间。Malik等[14]指出，用Boltzmann- Matano方法求得的扩散系数， 主扩散系数误差约60%，交叉扩散系数误差更高达120%。因此，从图3可以看出，本文对主扩散系数的预测值与试验值的吻合度高于交叉扩散系数。

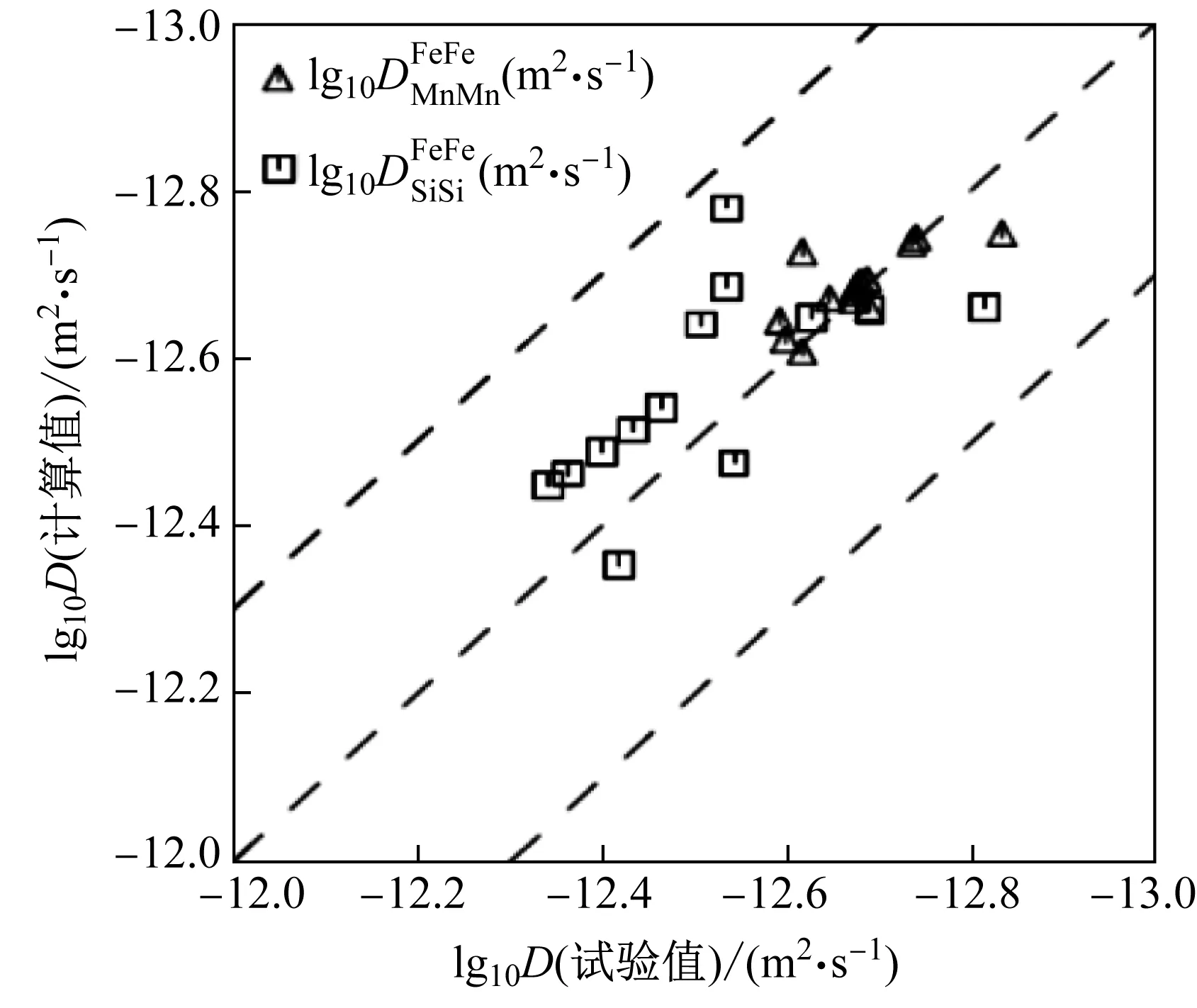
图3 Fe- Mn- Si三元系BCC相中主扩散系数的计算值与试验值[12]的比较Fig.3 Comparison between the calculated and measured[12] main interdiffusion coefficients in BCC phase Fe- Mn- Si alloys

采用优化的原子移动性参数计算得到的Fe- Mn- Si三元合金扩散偶的成分曲线如图4所示。可见，在1 273 K、125 h扩散退火条件下，本文预测的成分- 距离曲线与朱小和等[12]的试验数据吻合较好。这表明采用本文优化的原子移动性参数能够很好地预测Fe- Mn- Si三元系BCC相的扩散行为。

4 结论

(1)采用扩散偶技术制备了4对FCC相Fe- Mn- Al扩散偶，利用EPMA检测扩散偶扩散退火后的成分- 距离曲线，并合理外推得到了Fe- Mn- Al三元系FCC相的动力学数据库，模拟计算的成分曲线及扩散通道与试验数据均吻合较好，从而验证了所建数据库的可靠性。

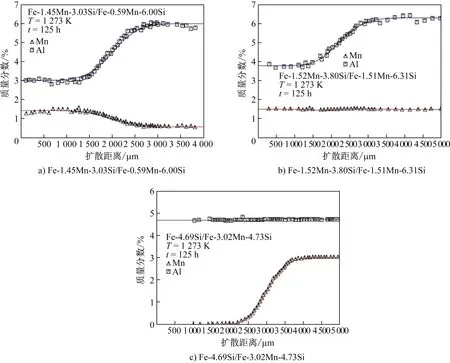
图4 扩散偶的成分- 距离曲线的计算值与试验数据[12]的比较Fig.4 Calculated concentration profiles of diffusion couples in comparison with the experimental data[12]