坡度对海底斜坡瞬态波浪响应及其滑动失稳特征影响研究❋
2020-05-28刘小丽尹清海刘洪睿
刘小丽, 尹清海, 刘洪睿
(1. 山东省海洋环境地质工程重点实验室(中国海洋大学),山东 青岛 266100; 2. 中国海洋大学环境科学与工程学院,山东 青岛 266100)
海底滑坡作为一种海洋地质灾害已逐渐成为近年来的研究热点,波浪是浅海地区触发海床不稳定性的重要因素之一[1-2]。
早在20世纪70年代,Henkel[3]即对密西西比河口海底滑动稳定性进行了分析,结果表明,即使水深达120 m,波浪也会使软土海床发生滑动失稳。Okusa和Yoshimura[4]基于波致海床瞬态响应的解析解分析了海床滑动稳定性,结果表明,砂土海床的滑动区在波谷位置,并指出,除非海底斜坡的坡度非常小,否则应考虑海床坡度导致波浪荷载变化的影响,但其并未对此开展进一步研究。
波致海底斜坡滑动稳定性分析中,大部分采用极限平衡法,将海床视为不变形的刚体进行计算[5-6]。刘博等[7]采用极限分析上限法,分析了波浪参数对海底斜坡滑动稳定性的影响。Zheng等[8]基于极限分析上限法,对波浪作用下海底灵敏性粘土边坡的滑动稳定性进行了分析,研究了波浪参数的影响,指出海底粘土边坡在极端波浪条件下更易失稳。Rahman等[9]采用概率方法,研究了粘性土海床和无粘性土海床滑动失稳的差异,结果表明无粘性土海床更易发生滑动失稳。刘小丽等[10-11]分析和探讨了不同滑动稳定性计算方法的优劣及其适用条件。
由于海底斜坡坡度较缓,坡角一般不超过10(°)[12],并考虑到波浪浅水效应分析的复杂性,因此,目前对海底斜坡滑动稳定性的研究中未考虑海底坡度导致的波浪荷载变化,即将海底斜坡面上的波浪荷载视为与水平海床面上的荷载一致,忽略了波浪沿斜坡面传播的浅水效应。相关文献表明,波浪沿斜坡面传播过程中,由于水深的不断变浅,会导致波浪发生变形甚至破碎,波浪的浅水效应明显[13-14]。与水平海床相比,波浪沿一定坡度斜坡面传播过程中的浅水效应,会导致斜坡面上波浪荷载的变化,进而引起海底斜坡瞬态波浪响应的变化,并进一步影响其滑动稳定性。不同坡度下,波浪浅水效应对海底斜坡瞬态响应及其稳定性的影响程度如何,目前未见相关研究。
鉴于此,基于波浪沿斜坡面传播的线性波浪理论,考虑波浪的浅水效应,分析不同坡度下海底斜坡波浪瞬态响应的特征,并对其滑动失稳特征的坡度效应进行研究。
1 海底斜坡滑动稳定性计算方法及验证
1.1 海底斜坡瞬态波浪响应计算模型
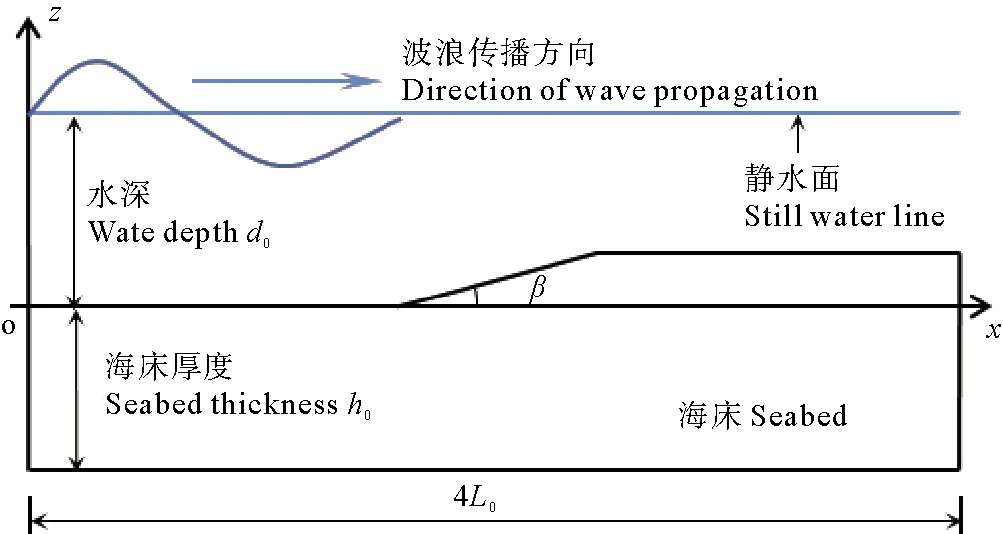
图1 波浪作用下海底斜坡几何模型示意图
基于经典小振幅波浪理论,波浪沿缓斜坡面传播过程中的波数k、波浪频率ω和水深d满足以下关系式[15]:
ω2=gktanh(kd)。
(1)
式中:ω=2π/T,T为波浪周期,在波浪传播过程中保持不变;k=2π/L;L为波长。
水深d变化时,对应的波高H与波浪爬坡前的初始波高H0、水深d0存在以下函数关系[15]:
(2)
式中k0=2π/L0。
对公式(1)进行求解,可得到不同水深d下的波数k;然后根据公式(2)可得到对应的波高H,进而可求得斜坡面上的波浪压力,其表达式如下:
(3)
基于Biot固结方程,波浪作用下海床瞬态响应的控制方程为[16]:
(4)
(5)
(6)
式中:u,w分别表示土体在x和z方向的位移;μ为泊松比;G为土的剪切模量;γw为孔隙水容重;p为波致瞬态孔隙水压力;n′为海床土孔隙率;K为渗透系数;t为时间;βs表示孔隙流体的压缩性,表达式为:
2016年,国务院总理李克强在政府工作报告中提出,“鼓励企业开展个性化定制、柔性化生产,培育精益求精的工匠精神”。[1]由此,“工匠精神”首次被政府提出,同时上升到国家发展层面,迅速成为舆论和社会争相关注的热点,并作为各行业严谨精确、锲而不舍的代名词。
(7)
其中:Kf表示水的体积压缩模量,一般取为1.9×109N/m2;Sr为饱和度;Pow表示绝对孔隙水压力。
海床两侧边界条件为:u=0;海床底部边界条件为:u=w=0;∂p/∂z=0;海床表面边界条件为:σ′z=τxz=0,p=Pb。
根据上述控制方程与边界条件,利用Comsol Multiphysics多物理场耦合有限元分析软件进行数值计算,可以得到波浪作用下海底斜坡应力状态。
1.2 海底斜坡滑动稳定性计算方法
根据相关研究[4],将波致海底斜坡的潜在滑动面视为圆弧面,图2为海底斜坡滑动面处微元土体的应力状态示意图,图中各应力均为波致应力与重力引起的应力之和,重力作用下斜坡体的应力亦通过有限元计算分析得到,图中正应力以拉为正。
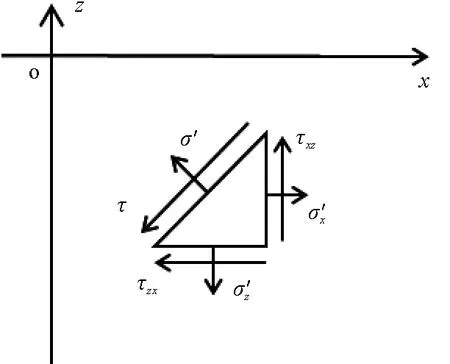
图2 斜坡滑动面上土体单元应力状态
利用微元体的应力平衡条件,可以得到斜坡土体滑动面上的有效正应力σ′和剪应力τ。根据摩尔-库伦抗剪强度理论,滑动面上微元体的抗滑力R及下滑力S分别为:
R=(c-σ′tanφ)·Δl,
(8)
S=τ′·Δl。
(9)
因为土体不能承受拉力,因此当σ′>0时,取为0。式中:c为斜坡土体的有效粘聚力;φ为斜坡土体的有效内摩擦角;Δl为微元体沿滑动面方向的长度,则沿某一潜在圆弧滑动面的斜坡体安全系数为:
(10)
式中n为沿该圆弧滑动面划分的微单元体个数,当Fs小于等于1时,沿该滑动面可能发生失稳滑动。
对海底斜坡不同位置的滑动面进行搜索,绘制所有滑动区的外包络线,该外包络线与海床面所包围的区域即为海底斜坡的滑动区。
1.3 稳定性计算结果验证
为了验证波致海底斜坡滑动稳定性数值计算结果的可靠性,以水平海床为研究对象,与基于海床瞬态波浪响应解析解[17]得到的海床滑动安全系数进行对比如下。
计算所用波浪和海床土体的参数为:高H=6.2 m,周期T=10 s,水深d0=10 m,对应的波长L0=92.33 m;海床厚度h0=18.47 m,泊松比μ=0.3,孔隙率n′=0.5,土体浮容重γ′=6 100 N/m3,剪切模量G=5.13×106Pa ,渗透系数K=10-5m/s,饱和度Sr=0.98,粘聚力c=0 Pa,有效内摩擦角φ=35°,孔隙水压缩模量Kf=1.9×109Pa。
针对海床中的不同潜在滑动面,数值计算结果与基于解析解计算得到的滑动稳定安全系数如表1中所示。根据计算结果可知,二者计算得到的安全系数基本一致,表明了数值计算结果的可靠性。
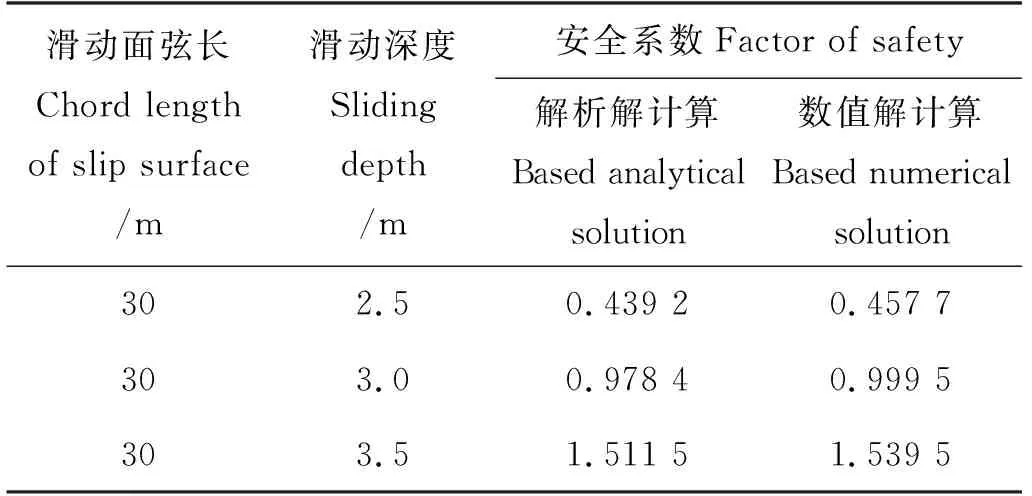
表1 基于海床应力解析解与数值解的安全系数对比Table 1 Comparison of factor of safety based on analytical and numerical solution of seabed stress
2 结果分析与讨论
2.1 坡度对海底斜坡瞬态波浪响应特征影响分析
以砂质海底斜坡为研究对象,计算参数如表2中所示。
对坡角分别为1°、2°、3°、4°和5°时斜坡体的波浪瞬态响应进行计算分析。图3是坡角为5°时,海底斜坡体的周期最大孔隙水压力、最大剪应力和最大水平位移的等值面分布图。
由于波浪沿斜坡面传播的浅水效应,导致波压力在斜坡坡顶水平段达到最大值,因此,从图3中可以看出,坡体的周期最大孔隙水压力和剪应力沿着斜坡面均有所增加,至坡顶水平段达到其最大值。最大孔隙水压力在海床表面处最大,随深度的增加其数值逐渐减小;最大剪应力随深度的变化趋势与海床的计算厚度有关,在本算例中,由于斜坡海床计算厚度相对较小,在0.2倍波长左右,因此剪应力随着深度的增加逐渐增大,并在海床底部达到峰值。海底斜坡体的瞬态剪应力与孔隙水压力随深度的变化规律与水平海床一致[18]。水平方向上,海底斜坡体的水平位移在坡顶角附近达到最大值;竖直方向上,土体水平位移随着深度的增加呈先增加后减小的变化规律。

表2 波浪与海床参数
分别对比斜坡的坡底水平段和坡顶水平段的周期最大剪应力差异程度和周期最大孔隙水压力的差异程度,结果如图4所示。
从图4可以看出,坡度对海底斜坡的瞬态波浪响应存在较为明显的影响。坡角为1°时,坡底与坡顶段土体的最大剪应力和孔隙水压力均存在6%左右差异,水平位移存在10%的差异;随着斜坡坡角的增大,坡底和坡顶段海床响应的差异程度迅速增加,坡角为5°时,坡底与坡顶海床土体最大剪应力的差异和最大孔隙水压力的差异均达到27%左右,水平位移的差异达到约51%。可见,随着海底斜坡坡度的增加,波浪沿斜坡面传播的浅水效应迅速增加,相对于水平海床,斜坡土体周期最大瞬态应力和孔隙水压力随着坡度的增加基本呈线性增加趋势;水平位移随着坡度的增加亦呈增加趋势,且当坡度大于一定数值后其增加速率会明显增大,表现出明显的非线性趋势。
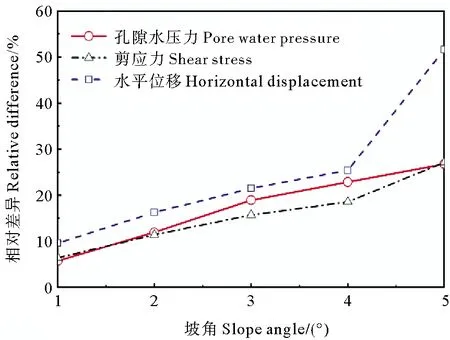
图4 海底斜坡坡底与坡顶瞬态波浪响应差异
2.2 坡度对海底斜坡滑动失稳特征影响分析
基于海底斜坡体的瞬态波浪响应,对坡角为1°、3°和5°时海底斜坡的滑动失稳区特征进行分析,结果如图5所示,图中给出了波浪作用时间分别为T/2和T时刻的滑动失稳区包络线分布图。
从图5可以看出,滑动区基本位于波谷。相比于坡底水平段滑动区,斜坡面上的滑动区深度和水平向滑动范围均有所增大,且随着坡度的增加,这种效应愈加明显。在本算例中,坡底水平段滑动深度约为1.7 m,水平方向的滑动范围约为45 m。当坡角为1°时,斜坡面上的滑动区深度为1.9 m,水平向滑动范围基本与坡底水平段相同;而当坡角为5°时,斜坡面上的滑动区深度约为2.5 m,滑动区水平向范围约为65 m,相对于坡底水平段滑动深度和水平向滑动范围,其数值分别增加了约47%和44%。随着坡度的增加,波浪的浅水效应逐渐增大,且斜坡体的重力场变化相对也更加明显,因此导致斜坡面上滑动区深度的逐渐增加和水平向滑动范围的不断增大。根据图5所示滑动区分布特征,可知在瞬态波浪响应下,海底斜坡极可能由于坡脚位置土体的失稳而发生牵引式滑动破坏;同时,坡体中上部土体可能沿着局部滑动面发生滑动。

图5 不同坡角下海底斜坡的滑动区
表3所示为海底斜坡的坡角为5°时,不同位置滑动面上的抗滑力与下滑力变化分析。从中可以看出,只有重力作用时,坡底和坡顶的水平段,滑动面上的下滑力很小,近似为零;在斜坡区和坡脚处的滑动面,由于海床具有一定的坡度,导致其下滑力有所增大。根据表3中数据可知,相比于只有重力场作用的情况,波浪场会引起海床土体沿滑动面抗滑力的下降和下滑力的增加,从而导致斜坡体在不同区域发生失稳滑动。
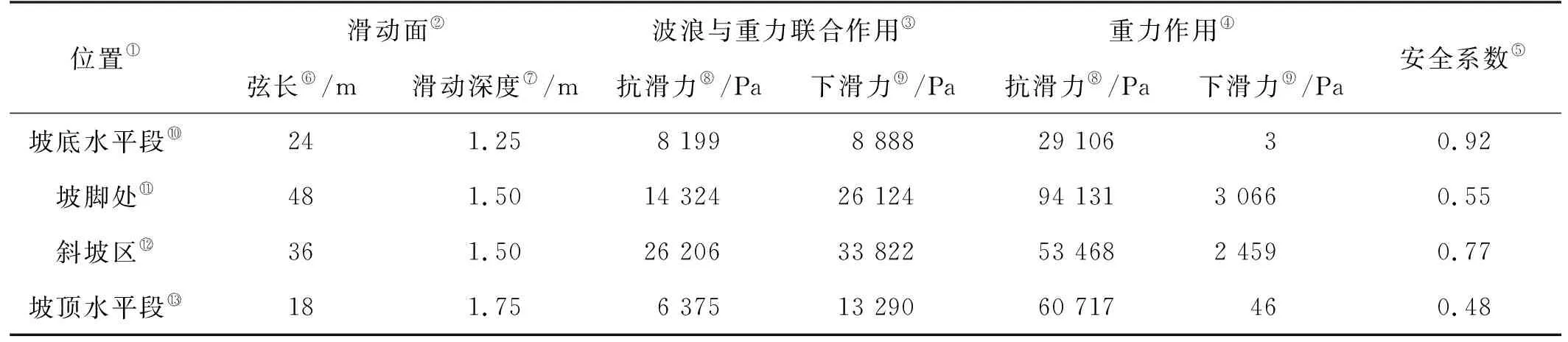
表3 滑动面上的下滑力与抗滑力比较
Note:①Location;②Slip surface;③Combination of wave and gravity;④Gravity;⑤Factor of safety;⑥Chord length;⑦Sliding depth;⑧Anti-sliding force;⑨Sliding force;⑩Flat section at bottom of the slope;Toe of the slope;Sloping area;Flat section at top of the slope
2.3 不同饱和度下海底斜坡滑动特征的坡度效应分析
对海床土的饱和度为1.0(饱和海床)和0.95(非饱和海床)时的海底斜坡滑动区特征进行分析,不同坡度下海底斜坡的最大滑动深度见图6。
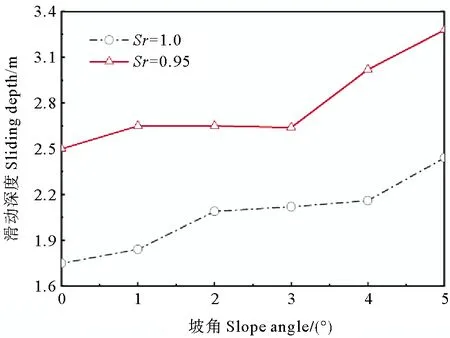
图6 不同饱和度下海底斜坡最大滑动深度
从图6中可以看出,饱和度不变时,随着坡角的增加,海底斜坡滑动区的最大滑动深度呈增加趋势。相对于饱和海床,非饱和条件下,海底斜坡的滑动深度更大,这与非饱和海床不同深度处的瞬态波浪响应存在相位滞后现象有较大关系[18]。
图6中,饱和度为1.0时,相对于坡角为0°的水平海床,坡角为1°时,斜坡最大滑动深度增加约5%;坡角为2°时,最大滑动深度增加约19%。饱和度为0.95时,相对于坡角为0°的水平海床,坡角为1°~3°时,斜坡滑动区深度增加量基本相同,约为6%;当坡角为4°时,滑动区深度增加约21%。故在此算例中,对于饱和度为1.0的海床,当其坡角超过1°后,坡度效应即已较为明显;而对于饱和度为0.95的海床,当其坡角大于3°后,其坡度效应才较为显著,即相对于饱和海床而言,坡度对非饱和海床滑动失稳特征的影响程度有所降低。分析其原因,在于非饱和海床条件下,海底斜坡的滑动深度普遍较大,相比之下,坡度的少量增加所导致的斜坡滑动深度增加效应相对不明显,只有当坡角达到一定数值后,坡度对斜坡滑动深度的影响才会表现得较为明显。
3 结论
考虑波浪沿斜坡面传播过程的浅水效应,基于海底斜坡体的有效应力状态计算其滑动稳定性,分析了不同坡度下海底斜坡瞬态波浪响应及其滑动特征,并对坡度的影响机制进行了分析,主要得到以下结论:
(1)坡度对海床瞬态波浪响应的影响较为明显。基于沿斜坡面传播的线性波浪理论计算可知,随着坡度的增加,波浪的浅水效应明显增加,相对于水平海床,斜坡体的周期最大瞬态应力和孔隙水压力随着坡度的增加基本呈线性增加趋势;斜坡体水平位移随坡度的增加呈非线性增加趋势。
(2)海床瞬态波浪响应下,滑动区基本位于波谷位置,相比于坡底水平段海床的滑动区,斜坡面上滑动区的深度和水平方向滑动范围均有所增加,且坡度越大,这种效应越明显,这与波浪沿斜坡面传播的浅水效应和坡体重力场的变化相关。
(3)饱和度对海底斜坡的失稳滑动特征有较大影响,相对于饱和海床,非饱和条件下海底斜坡体的滑动深度更大,且坡度对斜坡滑动特征的影响程度有所降低。
