空间约束密度聚类的超像素分割算法

韩剑辉　唐俊超

摘 要：超像素分割是计算机图像处理的一个重要的预处理步骤，传统的基于密度聚类的超像素分割算法对于边界的处理比较好，但是所获得的超像素形状不规则，针对其缺点，提出了一种空间约束的DBSCAN聚类的超像素分割算法。首先在图像上均匀的播撒种子点，之后以种子点为中心利用空间约束的密度聚类逐步向外扩张，直至遍布整张图像，获得初始的超像素，通过k-means方法迭代进行更新种子点，最后遍历种子点来清理掉未访问过的像素点。为了验证方法的有效性，在BSDS500数据集进行实验，并与当前最先进的方法进行了定性和定量的对比。在超像素数目为300左右时，该方法的紧密度为0.45，明显优于传统的基于密度聚类的超像素分割算法的0.40。空间约束密度聚类的超像素分割算法在通过均匀分布的种子点以及空间约束后使得紧密度得到了明显的提高。

关键词：图像分割;超像素;密度聚类;k-means;空间约束

DOI：10.15938/j.jhust.2020.06.019

中图分类号： TP391

文献标志码： A

文章编号： 1007-2683（2020）06-0131-06

Superpixel Segmentation Algorithm by

Spatial Constrained Density Clustering

HAN Jian-hui， TANG Jun-chao

（School of Computer Science and Technology， Harbin University of Science and Technology， Harbin 150080， China）

Abstract：The superpixel segmentation is an important pre-processing step in computer image processing. The traditional superpixel segmentation algorithm based on density clustering is better for boundary processing， but the resulting superpixel shape is irregular. In view of its disadvantages， a new algorithm of superpixel segmentation combining k-means and DBSCAN clustering with spatial constraints is proposed. We first spread the seed point evenly on the image， and then gradually expand the density cluster centered on the seed point using spatial constraints until the entire image is spread， the initial superpixels are obtained， and the seed point is updated iteratively through the k-means method. Finally we traverse the seed point to clean up unaccessed pixels. In order to verify the effectiveness of the algorithm ， experiments were conducted in the BSDS500 dataset and qualitative and quantitative comparisons were made with the most advanced algorithms . When the number of superpixels is about 300， the compact density of this method is 0.45， which is significantly better than the 0.40 of the traditional superpixel segmentation algorithm based on density clustering.In this paper， the algorithm of superpixel segmentation is presented to increase the compact density by the uniform distribution of seed points and spatial constraints.

Keywords：image segmentation;superpixel;density clustering;k-means;spatial constraint

0 引 言

超像素[1]是2003年由Xiaofeng Ren提出并發展起来的一种图像分割技术，指由具有亮度、纹理、颜色和其他类似图像特征的像素组成的不规则像素块[2-3]。传统的图像处理多数以像素为基本单位，而超像素则以区域为基本单位，很大程度上减少了后续图像处理的复杂度，被应用于对象追踪[4]、物体分割[5]、人脸检测[6]等诸多方面。

目前的超像素分割算法分为两种类型，其中一种基于梯度的变化，包括简单的线性迭代聚类（simple linear itrative clustering，SLIC）[7]，分水岭（watersheds，WS）[8]，空间约束的分水岭（watersheds superpixel，SCOW）[9]，均值漂移（mean shift，MS）[10]，TurboPixels[11]等。另一种则是基于图论的，包括懒惰随机游走（lazy random walk，LRW）[12]，TPS[13]，超像素格子（superpixel lattice，SL）[14]，熵率超像素（entropy rate superpixel，ERS）[15]，归一化割（normalized cut，NC）[16]，Graph-based[17]等。

基于梯度的超像素大多数从像素的初始聚类开始，通过梯度变化的方法迭代更新聚类，直到满足某些标准形成超像素。SLIC[7]是基于k-means聚类的超像素分割算法，特点是可以控制超像素块的数目与紧密度，缺点是它只考虑了像素点与种子点之间颜色和坐标之间的关系，没有考虑到像素点与边界之间的关系，对于图像边界的贴合度不是很好。SCOW[9]是基于空间约束的分水岭方法，特点是超像素的形状较为规范，算法的速度快，缺点是无法控制超像素的数目。TurboPixels[11]的算法将空间约束引入到水平集演化中，用来获得紧凑的超像素，缺点是所获得的超像素与图像的边界重合较差。

基于图论的超像素是将图像描述为一张带有权值的无向图，图像中每一个像素点对应于图中的一个节点，像素点之间的相邻关系对应于图的边，通过使用不同的分割方法来对图中的节点进行划分，这样完成对图像的分割。TPS[13]是保留了拓扑及规律的方法，优点是超像素的形状较为规范，缺点是需要预先提取图像的边界，浪费很多的时间并且图像边界的重合不好。LRW[12]在随机游走算法的基础之上加入了自跳过程，对于图像的纹理捕捉较好，缺点是算法速度慢。ERS[15]将超像素分割问题制定为目标函数，包括在图上游走的熵率以及平衡项，缺点是所获得的超像素形状不规则。

基于k-means聚类的超像素分割算法原理简单，缺点是没有考虑图像的边界信息，图像边界重合较差;基于密度聚类[18]的超像素分割算法DBSCAN[19]，由于DBSCAN聚类算法可以找到任意形状的簇，因此它具有很好的分割复杂和不规则形状对象的潜力，但没有考虑像素点与种子点间的空间关系，导致超像素形状不规则。

本文的主要贡献如下：

1）提出了一种基于空间约束的DBSCAN与k-means的混合聚类超像素算法，该算法的聚类过程在DBSCAN算法上加入了空间约束，使得超像素的形状更加规则。

2）在该算法中，将图像分成了K个区域，使得超像素的数目得到了控制。

3）在该算法中，使用k-means算法进行种子点更新，解决了噪声对于DBSCAN算法的影响。

4）在该算法中，清理小区域阶段，将未访问过的像素点与种子点进行计算，有效地提升了分割效果。

5）在测试算法时，使用了BSDS500数据集进行测试，结果表明，本文算法SCDC的紧密度系数明显优于DBSCAN。

1 聚类阶段

本文的算法需要将要处理的图像转换到LAB颜色空间，LAB颜色空间中的L分量用于表示像素的亮度从黑到白，取值为[0， 100];A表示从绿色到红色的范围，取值为[-128，127];B表示从黄色到蓝色的范围，取值为[-128，127]。相较于RGB颜色空间，LAB空间表示的颜色范围更广，因此本文选用LAB颜色空间进行计算。

将人工设定的K个种子点均匀的分布于整张图象之上，K的取值范围为[0， N]，其中N为图像中像素点的数目，相邻种子点的间距近似为s=N/K，K为人为设定的超像素块的数目。为了让算法尽快的收敛，将由种子点出发对于像素点的搜索范围限制在2s×2s的范围内。

在聚类阶段，有4个集合，即已访问集合V和未访问集合NV，种子点集合以及标记集合。其中种子点集合存入的是所有种子的[l， a， b， r， c]信息，标记集合在每一次种子点更换时都会被重置，V∩NV=，V∪NV=Ps，Ps为全体像素。先将种子置为已访问状态，之后将其存入标记集合，这样就在以该种子为中心的区域内得到了4种点，即已访问点，未访问点，种子点以及标记点。按顺序找到标记点在未访问集合NV中相邻的4个像素，首先将它们置为已访问状态，之后计算它们与种子点该标记点的组合距离，如果小于阈值的话就将其存入标记集合。终止条件为标记集合不再存入像素点。如此反复，直到遍历完毕所有种子点。

dist1=（Lp-LC）2+（AP-AC）2+（BP-BC）2（1）

dist2=（LP-LS）2+（AP-AS）2+（BP-BS）2（2）

dS=（rp-rS）2+（cp-cS）2（3）

D=dist1+γdist2·exp（-αdS）（4）

在式（1）中，LP，AP，BP代表像素点P的颜色特征;LC，AC，BC代表的是标记点C的颜色特征。在式（2）中，LS，AS，BS代表的是种子点S的颜色特征。在式（3）中，rp，cp代表的是像素点P的空间特征;rS，cS代表的是种子点S的空间特征。在式（4）中，α為空间参数，用于调节空间约束的强度;γ为种子约束参数，用于调节像素点P所受种子点约束的强度。dist1是像素点P与标记点C的色彩距离，dist2是像素点P与种子点S的色彩距离，dS是像素点P与种子点S的空间上的距离，D是在加入了空间约束后像素点P到标记点与到种子点的组合距离。

通过式（4）可以看出，空间约束使像素点P所受种子点的约束随着与种子点之间的距离而发生变化，距离种子点越远，它所受到种子点的约束就越小，解决了边界附近没有空间约束导致的超像素形状不规则问题，这样就可以在传统密度聚类分割的超像素的基础之上得到形状更加规则的超像素。

Cseed=∑pi∈CseedpiCseed（5）

在上述步骤进行完毕之后，通过k-means算法来更新种子点，如式（5）所示，其中pi为属于Cseed的像素，|Cseed|为属于Cseed的像素数目，在公式左侧的Cseed为新的种子点。在更新完种子点后，对前面聚类及更新种子点的步骤进行迭代来改善DBSCAN对于初始种子点的选择过于敏感的缺点。

2 清理小区域阶段

在清理小区域阶段，由于本文算法是以种子点为中心向4邻域进行生长的，所以会出现“空洞”。采用如下的公式依次遍历未访问到的像素点与所有种子点之间的组合距离，通过对比得到其中最小距离，则该像素点属于这个距离所对应的种子点。

d1=（rp-ri）2+（cp-ci）2（6）

d2=（LP-Li）2+（AP-Ai）2+（BP-Bi）2（7）

d=d12+d22β（8）

式中：rp，cp为像素点P的空间特征;ri，ci为种子点i的空间特征。LP，AP，BP为像素点P的颜色特征;Li，Ai，Bi为种子点i的颜色特征。d1为像素点P到种子点i的色彩上的距离;d2为像素点P到种子点i的空间上的距离;β为参数，调节颜色距离所占的权重。

3 实验结果

在本节中，首先对SCDC中的参数进行了分析，然后将SCDC与最先进的算法进行比较，包括SLIC[7]，DBSCAN[19]，TPS[13]，他们的实验结果通过运行原作者提供的公开代码以及其所设置的默认参数获得。所有实验均在BSDS500数据集[20]上进行。

3.1 参数分析

在本节中，我们评估空间约束强度对于实验结果的影响。α控制着空间约束强度的大小，将α分别设置为0，0.1，1进行实验。

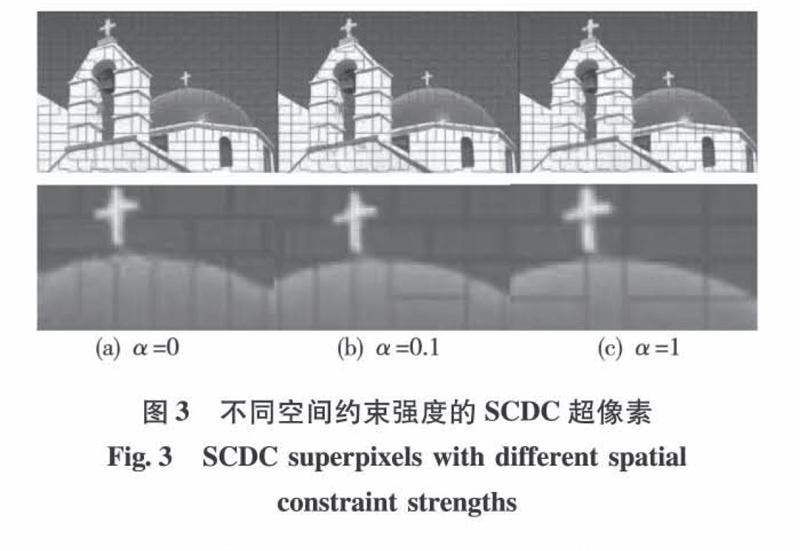
如图3所示，当α=0时，即空间约束强度为0的时候，图3（a）中局部放大图在十字架底部显得杂乱无章;当α=0.1的时候，图3（b）中十字架被清晰的分割了出来;当α=1时，空间约束过于强大，图3（c）中十字架没有被分割出来。在后面的实验中，为了平衡超像素规则的形状和对于图像边界的贴合，我们取α=0.5×10-6。

3.2 与其他先进的超像素算法进行比较

我们将参数设置为E=49，α=0.5×10-6，γ=1.450，β=2.5，与SLIC[7]，DBSCAN[19]，TPS[13]这3种目前最先进的超像素分割算法算法进行比较。

3.2.1 视觉比较

图4给出了由SLIC，TPS，DBSCAN和本文算法分割的超像素的视觉结果。从图中可以看出，本文算法对于图像边界的重合程度明显强于TPS算法;本文算法所生成的超像素明显比DBSCAN更加规则。传统的基于DBSCAN的超像素生成算法只考虑到了像素点之间的颜色关系，它的像素点到种子点的权值是固定不变的，所以其超像素的形状不规范。TPS过于注重形状上的规则，导致其对于图像边界的重合较差。本文算法在DBSCAN对于边界重合的基础之上有效控制了超像素块的形状。

如图5所示，虽然这些算法都能产生紧凑且均匀的超像素，但是這些超像素算法（如DBSCAN和TPS）难以实现兼顾图像边界和规则性的良好性能。本文算法中考虑了空间约束，因此在保持较高边界重合的同时形状更规则。在放大的区域处清楚地表明，本文算法比SLIC，DBSCAN及TPS的综合表现更好。

3.2.2 定量比较

在超像素分割中采用4种常用的标准来对这几种算法进行评估，分别是边界召回率（boundary recall，BR）[21]，欠分割错误率（undersegmrntation error，UE）[22-23]，紧密度（compactness，CO）[24]和可达分割精度（achievable segmentation accuracy，ASA）[15]。

边界召回率BR[21]是用来衡量超像素算法所产生的超像素对于图像边界真值重合性能的重要指标，较高的边界召回率代表了对图像ground truth更好的重合，即越高越好。由图6（b）可以得出我们的超像素方法的边界召回率明显高于TPS算法。

欠分割错误率UE[22-23]用来衡量从图像ground truth“泄漏”的像素百分比，一个好的超像素算法应该尽可能减少分割结果中的欠分割区域。换句话说，我们需要保护超像素仅与一个图像真值区域重合，即UE越低越好。由图6（d）可以看出本文算法的欠分割错误率略高于其他3种方法。

紧密度CO[24]表示了超像素块的规则程度，越高越好。由图6（c）可以看出在加入了空间约束后，本文算法的紧密度明显高于DBSCAN，这说明超像素的边界得到了控制，本文的超像素分割较DBSCAN更规则。

可达分割精度ASA[15]用来衡量计算超像素块作为图像的基本单位时，与图像ground truth的最大重合程度，即越高越好。由图6（a）可以看出，本文算法的ASA与DBSCAN及TPS差距很小。

4 结 论

针对DBSCAN超像素分割算法所获得的超像素块形状不规则的缺点提出了一种基于空间约束DBSCAN新型超像素生成算法。我们使用伯克利分割数据库BSDS500对4个常用指标进行了评估，本文算法对于不同复杂程度的图像均能获得比较好的分割效果。在未来，我们将继续在基于密度聚类的基础上开发出更加高效超像素分割算法。

参考文献：

[1] REN X ， MALIK J . Learning a Classification Model for Segmentation[J]. Iccv， 2003（1）：10.

[2] STUTZ D ， HERMANS A ， LEIBE B . Superpixels： An Evaluation of the State-of-the-Art[J]. Computer Vision and Image Understanding， 2017：S1077314217300589.

[3] WANG M ， LIU X ， GAO Y ， et al. Superpixel Segmentation： A Benchmark[J]. Signal Processing： Image Communication， 2017， 56：28.

[4] YANG F， LU H， YANG M H. Robust Superpixel Tracking[J]. IEEE Transactions on Image Processing， 2014， 23（4）：1639.

[5] LU L . A Nonparametric Treatment for Location/Segmentation Based Visual Tracking[C]// IEEE Conference on Computer Vision & Pattern Recognition. IEEE， 2007.

[6] 林克正， 魏穎， 程卫月. 压缩感知的人脸图像去噪[J]. 哈尔滨理工大学学报， 2015（5）：91.

LIN Kezheng， WEI Ying， CHENG Weiyue. Face Image Denoising of Compressed Sensing[J]. Journal of Harbin University of Science and Technology， 2015（5）：91.

[7] ACHANTA R ， SHAJI A ， SMITH K ， et al. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2012， 34（11）：2274.

[8] VINCENT L ， SOILLE P . Watersheds in Digital Spaces： an Efficient Algorithm Based on Immersion Simulations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 1991， 13（6）：583.

[9] HU Z ， ZOU Q ， LI Q . Watershed Superpixel[C]// IEEE International Conference on Image Processinging （ICIP）. IEEE， 2015：349.

[10]COMANICIU D， MEER P. Mean Shift： A Robust Approach Toward Feature Space Analysis[J]. IEEE Trans Pattern Analysis & Machine Intelligence， 2002， 24（5）：603.

[11]LEVINSHTEIN A ， STERE A ， KUTULAKOS K N ， et al. TurboPixels： Fast Superpixels Using Geometric Flows[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2009， 31（12）：2290.

[12]SHEN J ， DU Y ， WANG W ， et al. Lazy Random Walks for Superpixel Segmentation[J]. IEEE Transactions on Image Processing， 2014， 23（4）：1451.

[13]DAI T， FU H， CAO X. Topology Preserved Regular Superpixel[C]// IEEE International Conference on Multimedia & Expo.， 2012：765.

[14]MOORE A P ， PRINCE S J D ， WARRELL J ， et al. Superpixel lattices[C]// 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition （CVPR 2008）， Anchorage， Alaska， USA. June 24-26， 2008：1.

[15]LIU M Y， TUZEL O， RAMALINGAM S， et al. Entropy Rate Superpixel Segmentation[C]// Computer Vision & Pattern Recognition， 2011：2097.

[16]SHI J ， MALIK J . Normalized Cuts and Image Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2000， 22（8）：888.

[17]FELZENSZWALB P F ， HUTTENLOCHER D P . Efficient Graph-Based Image Segmentation[J]. International Journal of Computer Vision， 2004， 59（2）：167.

[18]ESTER M. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise[C]//Proc.Int.Conf.Knowledg Discovery & Data Mining， 1996： 226.

[19]SHEN J， HAO X， LIANG Z， et al. Real-time Superpixel Segmentation by DBSCAN Clustering Algorithm[J]. IEEE Transactions on Image Processing， 2016， 25（12）： 5933.

[20]ARBELAEZ P ， MAIRE M ， FOWLKES C ， et al. Contour Detection and Hierarchical Image Segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2011， 33（5）：898.

[21]MARTIN D R ， FOWLKES C C ， MALIK J . Learning to Detect Natural Image Boundaries Using Local Brightness， Color， and Texture Cues[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2004， 26（5）：530.

[22]NEUBERT P ， PROTZEL P . Compact Watershed and Preemptive SLIC： On Improving Trade-offs of Superpixel Segmentation Algorithms[C]// 2014 22nd International Conference on Pattern Recognition （ICPR）. IEEE Computer Society， 2014：996.

[23]BERGH M V D ， BOIX X ， ROIG G ， et al. SEEDS： Superpixels Extracted via Energy-Driven Sampling[C]// European Conference on Computer Vision. Springer， Berlin， Heidelberg， 2012：13.

[24]RAND W M. Objective Criteria for the Evaluation of Clustering Methods[J]. Journal of the American Statistical Association， 1971， 66（336）： 846.

（編辑：温泽宇）

收稿日期： 2019-05-23

基金项目： 国家自然科学基金（61502124）.

作者简介：

韩剑辉（1962—），男，教授，硕士研究生导师.

通信作者：

唐俊超（1994—），男，硕士研究生，E-mail：2609307954@qq.com.