鼓形轮轮压作用点在型钢轨道上的位置的分析计算

2020-05-26张战前

卷宗 2020年8期

摘要：通过鼓形车轮在工字钢下翼缘上运行的工况，利用几何法做出了三个直角三角形，通过相似三角形的推论证明了这三个直角三角形相似，从而又利用一个直角三角形的两个直角边与工字钢斜面斜度的关系，将已知参数（工字钢斜面斜率）引入，最后推导出工字钢与鼓形车轮的接触系数;从而得到了鼓形车轮与工字钢和槽钢接触时的力作用点;举例计算鼓形轮在槽钢上的计算，并将常用型钢与鼓轮的接触系数值列于表1中，方便计算时查找使用。

关键词：轻小型起重机;鼓形车轮;翼缘斜面;

做为起重机生产单位，为了满足使用单位的要求，需要对其原有的结构进行进行校核计算;同时起重机作为特重设备，也为了安全期间，无论出于何种考虑，都需要进行计算作为理论基础。

因此本文有必要针对鼓形轮在工字钢轨道下翼缘运行时的条件为研究对象，来分析其接触系数μ及其它型钢轨道的接触系数μ值大小，即鼓形轮在型钢翼缘斜面上力的作用点位置。

1 计算模型图1

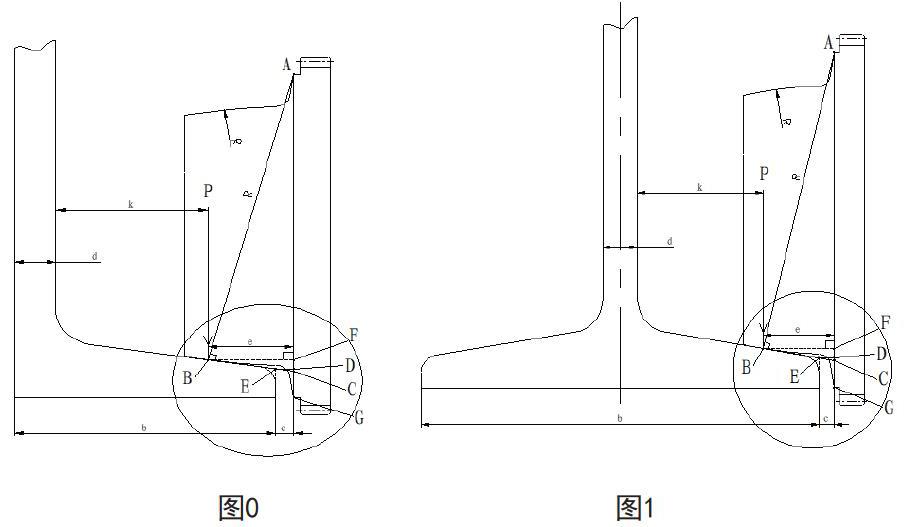
计算模型如图1所示：工字钢下翼缘的宽度为b腹板厚度为d，鼓形车轮的圆弧曲率半径为R，车轮图上的A点与工字钢下翼缘最外边的水平间距为c，通常其间隙c取3～5mm，最大间隙按5mm取值;当鼓形车轮的圆弧面与轨道工字钢的斜面接触时，一定会有一个交点即接触点B，同时B点也是鼓形车轮圆弧面与轨道工字钢斜面的切点;由车图设计图纸可知，线段AB为鼓形车轮的圆弧曲率半径为R，圆心为A点，于此同时，由于工字钢下翼缘斜面线为过圆弧切点切线，所以工字钢下翼缘斜面线与线段AB垂直;线段AG为边圆弧圆心的铅垂线;本文所需要分析推导的结论是：轮压作用点与工字钢腹板内侧的距离k。

2 计算模型图2

将计算模型图1中的局部放大如图2所示：将工字钢下翼缘斜面线沿长并与铅垂线AG相交于C点，再将工字钢翼缘最外侧沿铅垂方向向上沿长并与工字钢下翼缘斜面沿长线相交于E点，再从E点作线段AG的垂线交于D点;从B点作线段AG的垂线交于F点。

3 计算模型图3

根据对以上图1和图2 分析，可得到图3所示三个直角三角形;分别为图3（a）中的直角三角形EDC，图3（b）中的直角三角形ABC，图3（c）中的直角三角形ABF。

4 综合分析计算

根据对以上图1和图2和图3可得出如下结果：

1）在图3（a）中的直角三角形ECD和图3（b）中的直角三角形ACB，因为∠ECD和∠ACB为共用角，所以∠ECD=∠ACB;根据相似三角形的推论：有一个锐角相等的两个直角三角形相似;又根据相似三角形的性质：相似三角形的对应角相等，对应边成比例，所以∠CED=∠CAB;在图3（b）中的直角三角形ACB和图3（c）中的直角三角形ABF，因为∠CAB和∠BAF為共用角，所以∠CAB =∠BAF;根据相似三角形的推论：有一个锐角相等的两个直角三角形相似;又根据相似三角形的性质：相似三角形的对应角相等，对应边成比例，所以∠CAB =∠BAD;最终推出∠BAF=∠CAB=∠CED和图3中的（a）、（b）、（c）三个直角三角形相似。

2）在图3（a）中的直角三角形ECD，边长DE=c，边长EC为工字钢下翼缘斜面线，所以CD/DE为工字钢下翼缘斜面线的斜率x;

∴最终可得到轮压作用点与工字钢腹板内侧的距离：（如图1）

同理可以写出轮压作用点与槽钢腹板内侧的距离：（如图0）

利用公式⑴，

将鼓形车轮在几种常用型钢轨道上运行时的接触系数μ值计算出来列入表1。

4 结论

1）通过以上分析计算可知：要求出轮压作用点与工字钢腹板内侧的距离k，通过上面的式子⑵、⑶可以看出：b、d、c、R分别为型钢尺寸和车轮圆弧曲率半径，选择过型钢和车轮后，全部就是已知的数。所以只有接触系数μ值为未知数，而型钢确定后μ值可通过式子⑴将型钢接触面的斜度x代入计算出来，也可通过表1查取。

2）当鼓形车轮在型钢轨道上运行时，车轮圆弧曲率半径不变时，接触系数μ值越大轮压作用点就越靠近型钢内腹板位置，对型钢翼缘受力越有利;反之就越远离型钢内腹板位置，对型钢翼缘受力越有不利。

3）宫本智主编的《葫芦式起重机》一书上的轻型工字钢触系数0.118，应修改为0.119比较恰当。

参考文献

[1]宫本智.葫芦式起重机[M].天津：天津科学出版社，2009.

[2]王金诺，于兰峰.起重运输机金属结构[M].北京：中国铁道出版社，2002.