基于背景感知与快速尺寸判别的相关滤波跟踪算法

王永雄 ，冯 汉

（1.上海理工大学光电信息与计算机工程学院，上海，200093；2.上海康复器械工程技术研究中心，上海，200093）

引 言

相关滤波(Correlation filters,CF[1])首次被应用到目标跟踪就取得很好的跟踪效果，产生了极大的反响。Henriques等在此基础上引入循环移位操作和核技巧(Circulant structure of tracking-by-detection with kernel,CSK[2])极大增加了训练样本集并增强滤波器的性能，在后续的工作中他们提出了核相关滤波跟踪(High-speed tracking with kernelized correlation filters,KCF)算法[3]使用了更具鉴别力的快速梯度直方图特征(Fast HOG,FHOG[4])替代原先的灰度特征，进一步提高跟踪精度。Danelljan等[5]则利用颜色属性特征(Color name,CN[6])提出颜色自适应的思想,选取最有鉴别力的颜色特征进行跟踪，同样能取得较好的跟踪效果。另外近几年深度学习与相关滤波的结合在跟踪领域也取得越来越多的成果[7-9]。

相关滤波类跟踪算法在取得飞速发展的同时也有一些难点问题亟待解决，边界效应就是其中之一。边界效应的产生是由于循环移位过程中除了最原始的样本以外其余样本都是循环移位合成的，这样真实样本占比太少会导致训练结果不佳。实际应用中普遍通过扩大目标检测区域并且添加余弦窗抑制边界效应，这样只要在循环移位过程中保持目标的完整即可认为该样本合理。但是添加余弦窗会过滤掉了大量背景信息，极大降低了跟踪器的性能。Galoogahi等提出的背景感知相关滤波（Background-aware correlation filters,BACF）[10]算法巧妙地设计了一个裁剪矩阵P，在扩大检测区域的基础上进行循环移位操作，最后裁剪出合适的目标和背景信息。假设检测区域扩大后矢量化的维度为T，原始目标区域矢量化的维度为D，则被循环移位操作污染的样本只占，当T≫D时污染样本可以忽略不计。

BACF算法通过裁剪操作使得训练样本集的质量和数量都有极大的提高，能够精准预测目标位置变化。但是目标在移动过程中除了位置变化外，还会伴随着尺度变化，BACF算法通过多次重复计算多个尺度的目标区域获得最大响应，求得目标预测的位置及尺度。假设BACF算法单个尺度的位置预测运算时间为T，则N个尺度的计算时间约为N*T，该尺度检测策略严重影响目标的跟踪速度。本文针对此问题采用了Danelljan等[11]提出的平移加尺度滤波思想，设计了一个独立的一维尺度滤波器，充分利用了BACF算法的解决边界效应精准估计目标位置的优势，只计算单次BACF算法的目标位置估计，然后再利用尺度滤波器预测目标尺度变化。由于两个滤波器单独训练、局部优化，且尺度滤波器计算量远小于完整的BACF算法，假设尺度滤波器单次计算时间为TS(TS＜T),则本文算法单次计算时间约为T+TS，所以本文算法能在保证精准预测和目标尺度变化的同时极大提升目标的跟踪速度，与BACF算法相比，本文算法在不损失跟踪精度的基础上提高约75%的跟踪速度。

1 相关滤波器模型

1.1 传统相关滤波器模型

空间域相关滤波跟踪模型是通过最小化损失函数来找到适合的滤波器h，具体损失函数定义为

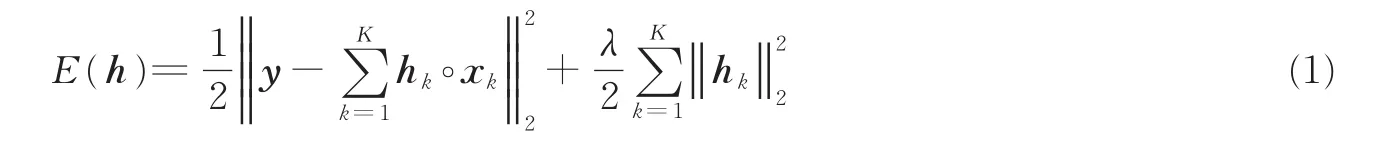
式中：y∈RD代表目标期望输出；K表示目标特征通道数；“∘”表示空间相关运算符；λ为正则化系数；xk∈RD，hk∈RD，分别表示第k个通道矢量化的训练样本和第k个通道的滤波器，D表示原训练样本单通道的维度。由于式(1)只针对一帧图像做优化，往往得不到鲁棒性高的滤波器，通过循环移位操作可以极大扩充训练样本集，提高滤波器的鲁棒性。添加循环移位操作后的损失函数定义为

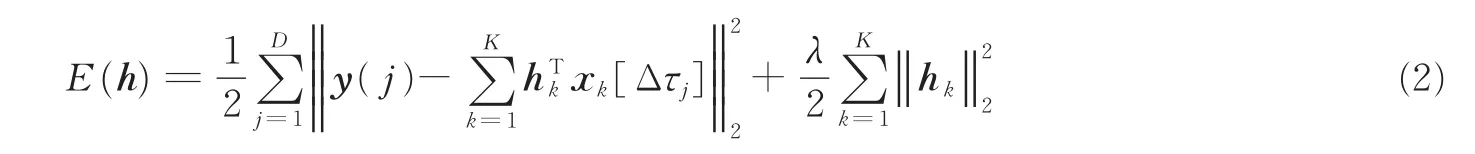
式中：[Δτj]代表第j次循环移位操作，y(j)代表期望输出的第j个元素，上标T代表转置操作。

1.2 背景感知相关滤波器模型

循环移位操作可以极大增加训练样本集，提高分类器性能，通过利用频域的相关性质[12]进行快速求解。通过引言部分介绍可知边界效应会极大削弱跟踪器的性能。不同于文献[11]采用1.1节所示的平移滤波器带有边界效应，本文采用BACF算法的思想，利用基于背景感知的平移滤波器，削弱边界效用，提升跟踪器性能。

利用基于背景感知的平移滤波器通过添加一个裁剪矩阵P裁剪出合适的训练样本，既能增加训练样本数量，又能极大提高训练样本的质量。添加裁剪矩阵P后的损失函数定义为

式中：P表示D×T的二值矩阵，T表示扩充后训练样本单通道的维度，其中T≫D；xk∈RD表示第k个通道训练样本。由于T≫D，所以滤波器h的尺寸远小于训练样本x的尺寸。

2 频域优化求解

2.1 频域投影

式(3)的求解计算量为O(D3K3)，不利于跟踪的实时性。通过利用复频域的性质可以有效减少计算量，式(3)在复频域的表达式为

式中：上标⌒运算符代表傅里叶变换，⊗运算符表示为克罗内克积，IK为K×K的单位矩阵，F为T×T的傅里叶变换系数矩阵，表示辅助变量。

为了求解式(4)，通过添加拉格朗日向量并利用增广拉格朗日方法(Augmented Lagrangian method,ALM)得到式(5)所示的增广拉格朗日式。

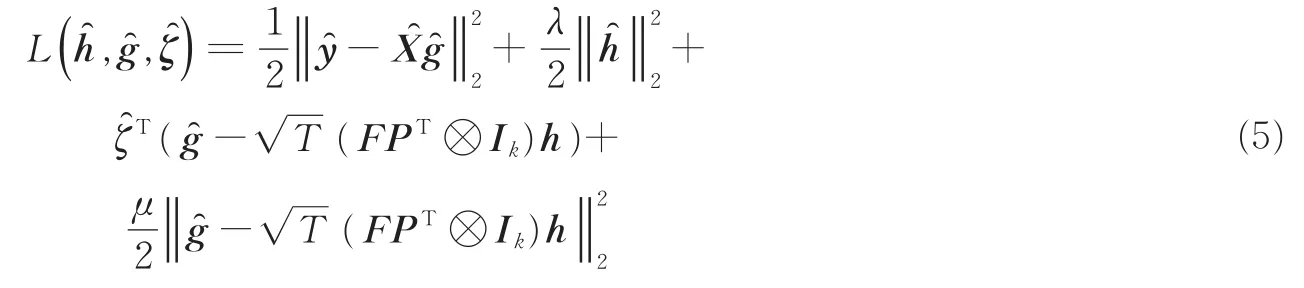
式中：μ为惩罚系数，拉格朗日向量大小为为第k个通道的拉格朗日向量的傅里叶变换形式。

2.2 优化求解

由于式（5）引入了裁剪矩阵P导致没有解析解，把原问题的求解过程转化为求解滤波器h和辅助变量g的两个子问题，再采用交替方向乘子法（Alternating direction method of multipliers,ADMM）求解此优化问题。

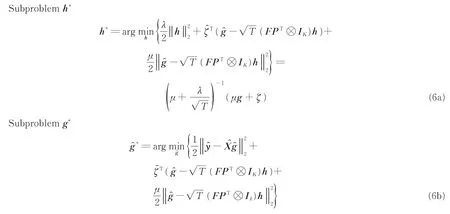
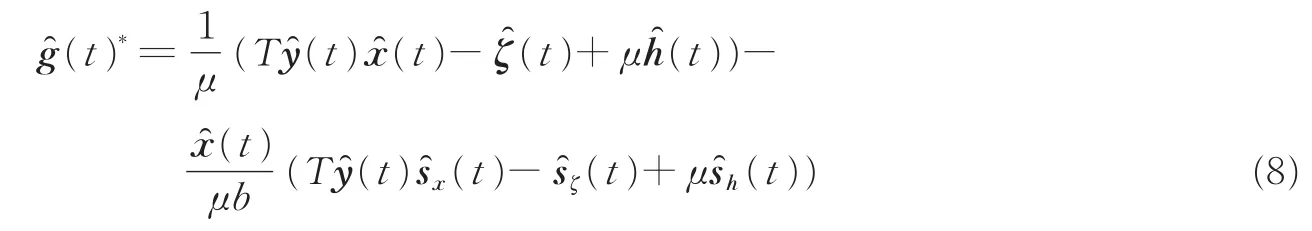
通过上述求解过程可知，计算量主要集中在两个子问题的优化过程。为了得到尺度变化，原BACF算法针对N个尺度求解N次优化问题将耗费大量的计算时间，因此原BACF算法跟踪速度较低。

3 尺度滤波器融合

上述介绍了BACF算法的建模及求解过程，解决了跟踪过程中的边界效应，可以精准估计目标位置变化。由于目标运动过程中还会伴随着尺度变化，如果不能精准且快速估计目标尺度变化仍会导致跟踪器不够完善。不同于原BACF算法利用平移滤波器在多尺度缩放的目标区域进行检测，需要对每个尺度做一次相关运算求解，导致消耗大量计算时间。本文将采用平移加尺度滤波的思想，额外训练一个一维尺度滤波器与平移滤波实现无缝融合，精准快速预测目标尺度变化。

3.1 尺度滤波器模型

尺度滤波器的建模与1.1节中传统核相关滤波器类似，通过计算尺度滤波器hs与训练样本f的相关运算结果，然后计算与期望输出gs的均方误差，最后通过均方误差最小化求得最优尺度滤波器hs，如式(9)所示。

式中：上标l代表第l个通道，λs为正则化常数，gs表示一维的高斯输出。式(9)是一个最小线性二乘问题，通过帕斯瓦尔定理转移到频域可以快速求解得到

式中：Hs,Gs,F分别代表滤波器hs，期望输出gs和训练样本f的傅里叶变换。求得滤波器hs后，采用如下更新策略进行更新

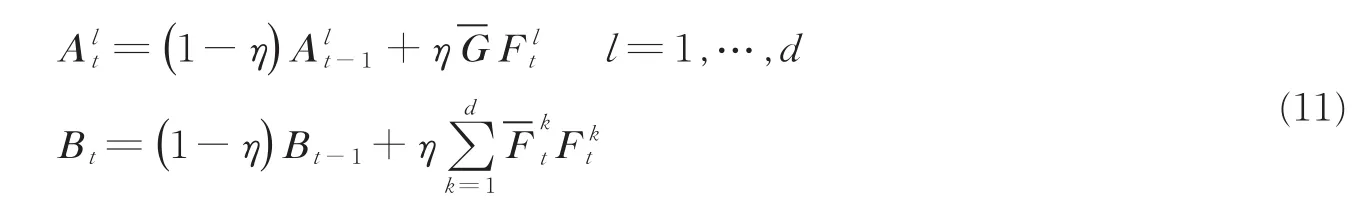
式中：At,Bt分别代表式(10)的分子、分母部分，η代表学习速率。式(10)给出了尺度滤波器hs的表达式，应用该滤波器到当前第t帧目标区域上进行相关运算将得到尺度响应输出ys，ys在复频域的表达式为

式中：d代表特征维度，下标t,t-1分别代表当前帧和上一帧代表当前帧目标区域的傅里叶变换，可以利用傅里叶反变换求得响应输出设P×R表示目标在第t-1帧尺度的宽和高，通过找到yt最大值所在的位置为n，则目标在第t帧尺度为：anP×anR，a为尺度因子。

3.2 尺度划分与降维

由于尺度系数an是指数函数，为非线性增长，可以实现对较大尺度进行粗检测，对较小尺度进行细检测。通过上述分析可知，仅通过对式(12)进行一次求解就能够预测目标的尺度变化。不同于式2.2节中平移滤波器需要大量优化迭代求解预测位置变化，式(12)具备解析解，能够快速求解尺度输出响应。如图1所示，图1(a)为原图，跟踪目标为行人；图1(b)利用平移滤波器在不同尺度上进行计算得到预测的尺度加位置，所需时间Ttotal=5×T(T为一次平移滤波器计算的时间，假设有5个尺度)；图1(c)在利用平移滤波器预测得到位置的基础上，再利用尺度滤波器预测目标尺度变化，所需时间Ttotal=T+Ts(T为一次平移滤波器计算的时间，Ts为预测尺度所需的时间)。由前面分析可知Ts≪T，所以平移加滤波的思想能够节省大量运算时间。

图1 尺度检测对比图Fig.1 Scale detection comparison

式(12)具备解析解可以快速预测目标的尺度变化，由于目标每一维的特征维度大小为P×R，但是需要划分的特征尺度个数为S，且P×R≫S，所以不同特征尺度之间有着极强的相关性，导致数据冗余，增添不必要的计算负担。为了削弱数据特征相关性，减小数据冗余，本文利用主成分析法(Principal component analysis，PCA[13])把特征向量降维为S维，再进行计算，从而极大减小了特征向量的维度，从而提高尺度检测速度。

4 实验结果与分析

为了有效评估本文算法的性能，实验中采用了VOT2014数据集，该数据集共有50段不同类型的跟踪场景，包含了光照变化、快速运动、运动模糊、尺度变化、背景相似干扰等常见的跟踪问题，同时采用视觉跟踪中最常用的3种评估方法来评估本文算法的性能指标：中心位置误差法（Center location error,CLE），距离精度法（Distance precision,DP）和重叠精度法（Overlap precision,OP）。CLE评价方法即计算目标预测位置(xp,yp)和真实位置(xr,yr)的平均欧式距离N为样本帧数；DP评价方法即计算CLE数据中小于一定阈值的帧数占总帧数的百分比，本实验取该阈值为20像素；OP评价方法即计算目标预测位置及大小与实际位置及大小的重叠率大于一定阈值的帧数占总帧数的百分比，该阈值一般选取PASCAL[14]的评价标准为0.5。同时为了直观对比本文算法的性能，本文选取了近几年优秀的几种算法做对比实验，包括以尺度变换为代表的DSST算法，解决边界效应的BACF算法，以循环移位操作和核技巧代表的KCF算法。各算法选取的特征均为FHOG[4]特征。

4.1 实验环境及参数设置

本实验的硬件平台为Inter(R)Core(TM)i7 2.90 GHz处理器，8 GB内存，软件平台为Matlab R2015a。第2节和第3节均选取FHOG特征作为目标的表现形式，FHOG特征cell大小为4，梯度直方图方向个数为9，2.2节中的ADMM优化过程中迭代次数设为2，惩罚因子μ设为1，本文的正则化系数λ和λs为0.001，第3节更新速率η为0.025，3.2节中尺度因子a为1.02。

4.2 定性分析

为了方便显示与对比算法的性能优劣，本实验首先选取实验视频集中6类代表不同特性的视频序列做定性分析，其中每个视频序列对应如表1所示的特性。

为了显示对比算法与本文算法的跟踪结果，选取表1中每个视频序列的3帧照片，如图2所示，其中图1（a）中不同颜色框代表不同跟踪算法。

表1 视频序列Table 1 Video Sequence

从图2可以直观看出本文算法有较高的鲁棒性，在目标经过遮挡、形变、运动模糊之后能持续跟准目标，KCF算法和DSST算法都有不同程度上的偏移，BACF算法鲁棒性也很高，但从Basketball和Coke序列中可以看出，经过姿态变化和大面积遮挡之后由于本文算法独立的尺度检测策略使得跟踪器能更好捕捉到目标的尺度变化，进而学习到更合适的背景与目标的占比，所以本文算法较BACF算法有更高的鲁棒性。

图2 定性分析图Fig.2 Qualitative analysis

4.3 定量分析

通过4.2的定性分析，可以直观粗略看出各算法性能，接下来将进行更细致的分析，通过计算上述提到的3种性能评估指标（CLE、DP、OP）来定量对比各算法性能差异，具体数据如表2所示。表2加粗部分数据为各对比算法中最优性能数据，从表2可以看出本文算法和BACF算法在CLE、DP、OP 3个指标中都能取得很好的成绩；从最后一行均值数据可以看出本文算法性能略优于BACF算法，而KCF[3]算法和DSST算法效果欠佳。

表2只给出了在20个像素阈值下的DP值，为了看出各对比算法的DP变化曲线以了解各跟踪器的鲁棒性，图3给出了在1～50个像素阈值下各个算法的DP曲线。从图3可以直观看出随着阈值的增加本文算法和BACF法DP曲线值趋近于1，性能明显强于KCF和DSST[10]算法。

在上述实验中为了具体直观对比显示只取了其中6个代表性视频序列做实验。为了不失一般性，本文对数据集中所有50个视频序列做了对比实验并求出CLE，DP，OP值。同时为了便于查看，给出了各算法3个性能指标均值，实验结果数据如表3所示。

表2 多种不同方法的性能指标对比Table 2 Multi algorithm performance comparison

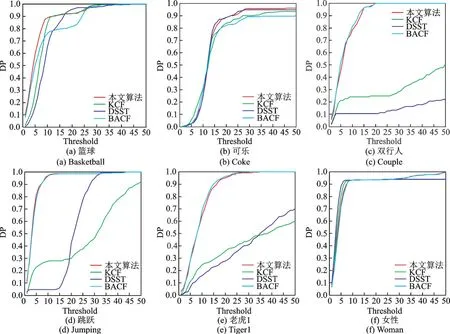
图3 在1～50个像素阈值下各个算法的DP曲线Fig.3 DP curves of different algorithms under 1—50 thresholds

从表3可以看出，在CLE和OP性能均值指标上本文算法略低于BACF算法1个像素和1个百分点，在DP性能均值指标上高于BACF算法2.6个百分点，KCF和DSST算法性能均远弱于本文算法和BACF算法。

表3 性能平均指标对比Table 3 Performance average index comparison

4.4 速度对比

本算法的最大优势在于不损失跟踪精度的前提下，极大地提升算法的跟踪速度，前几节主要以CLE，DP，OP三个性能指标来分析跟踪精度，可以看出本文算法与BACF算法在跟踪精度上差异不大，在CLE和OP性能均值指标上略低于BACF算法1个像素和1个百分点，在DP性能均值指标上高于BACF算法2.6个百分点。接下来通过实验数据分析各算法的跟踪速度，由于同一算法的跟踪速度在不同目标跟踪过程中的差异性并不大，本实验通过将表1中6个视频序列的跟踪速度的平均值作为最终结果再作对比，结果如表4所示。

表4 跟踪速度对比Table 4 Tracking speed comparison

从表4的跟踪速度可以看出，KCF算法的跟踪速度最快达到129 f/s，但是从前几节的对比实验可知其跟踪精度远低于本文算法和BACF算法。在跟踪速度上本文算法为21 f/s，而BACF算法为12 f/s，速度超出BACF算法75%，完全可以满足跟踪的实时性要求并且并不损失跟踪精度。

5 结束语

本文通过在传统BACF算法基础上融合尺度滤波器，既利用BACF算法的优势解决边界效应，精准估计目标位置变化，又利用尺度滤波器快速精准估计目标尺度变化，在不损失跟踪精度的同时极大提升了目标的跟踪速度。通过对比实验可以看出，本文算法能达到既快又好的跟踪效果。但是在跟踪过程中还有难点亟待解决，比如：长时间跟踪模板污染的问题，姿态、快速运动模板更新不及时，目标丢失再跟踪等，将是今后的研究方向。