几何特征保持的文物点云去噪算法

刘立恒，赵夫群，汤 慧，刘阳洋，耿国华

（1.西安交通大学电信学部，西安，710049；2.西安财经大学信息学院，西安，710100；3.西安财经大学实验实训教学中心，西安，710010；4.西北大学信息科学与技术学院，西安，710127）

引 言

随着三维激光扫描技术的日趋成熟和大众化，点云数据采集和预处理技术成为越来越受关注的研究热点，已被广泛应用于医学研究、文物数字化保护、地形勘探以及地震预测等领域[1-4]。在点云数据采集时，受物体本身的构造、粗糙程度和纹理以及光线等周围环境因素的影响，采集的原始点云往往含有大量的噪声点，这对后期的点云配准、融合以及三维重建等具有较大的影响，因此在保持点云的几何特征的基础上需要对其进行去噪处理。

点云数据去噪的目的是快速有效地删除噪声点，同时保持点云的纹理和边缘等特征细节。近年来，国内外学者提出了许多点云去噪算法。如，Ma[5]提出一种基于曲面拟合的去噪算法，具有较好的去噪效果和较低的时间复杂度；Wang等[6]提出一种基于Laplace分布的去噪算法，可以有效保留原始数据中有用细节信息；Cruz等[7]提出一种基于非局域增强卷积神经网络的去噪算法，通过结合卷积神经网络和非局部滤波器实现了图像的有效去噪；Centin等[8]提出一种几何保真的Signoroni网格去噪算法，该算法不依赖于点云规模，对目标应用领域具有挑战性的情况去噪效果良好；Zheng等[9]提出一种基于锐利特征骨架的点云去噪算法，该算法在保持重要几何特征不变的同时，能有效滤除噪声；王晓辉等[10]提出一种基于法向量距离估算的点云去噪算法，该算法采用加权局部最优投影算法对点云的平滑区域进行去噪，采用双边滤波算法对点云的尖锐区域进行滤波去噪，可以有效保持尖锐区域内的几何特征。以上这些算法均实现了点云数据的有效去噪，但对大尺度噪声和外点含量较高的复杂文物点云模型的去噪效果不佳。

针对文物点云数据模型，本文提出一种几何特征保持的去噪算法。对于大尺度噪声，即悬浮在主体点云周围且偏离主体点云的稀疏点，以及距离主体点云中心较远且小而密集的点，首先根据点云密度将点云进行栅格化划分，并确定每个点所在的栅格位置以及每个栅格中的点数，然后判断栅格内的点数及其周围栅格内点数的情况，删除大尺度噪声；对于小尺度噪声，即混合在主体点云中的噪声点，采用一种基于曲率因子和密度因子的特征加权模糊C均值聚类（Fuzzy C-means clustering,FCM）算法进行删除，从而实现点云的最终精确去噪处理。

1 基于栅格的大尺度噪声删除

大尺度噪声包含两部分：一部分是那些悬浮在主体点云周围且偏离主体点云的稀疏点；另一部分是距离主体点云中心较远且小而密集的点。对于大尺度噪声，这里采用栅格划分的方式进行删除。

1.1 栅格划分

对于点云P，其大尺度噪声采用栅格划分的方式删除。首先，将点云P中所有数据点的三维坐标点存到一个一维数组中，并构造一个与坐标轴平行的长方体包围盒，确保包围到点云的所有数据点。假设该长方体包围盒中点的最大和最小坐标分别为{xmax,ymax,zmax}和{xmin,ymin,zmin}，长方体栅格的长度为L。

然后，根据数据点的密度将长方体包围盒划分成多个小立方体栅格，如图1所示。那么小立方体栅格在x,y,z轴3个方向的个数Sumx,Sumy,Sumz为

对于点云P中的某一确定点其中表示点pi的三维坐标，那么点pi所在小立方体栅格在x,y,z轴3个方向的索引号为

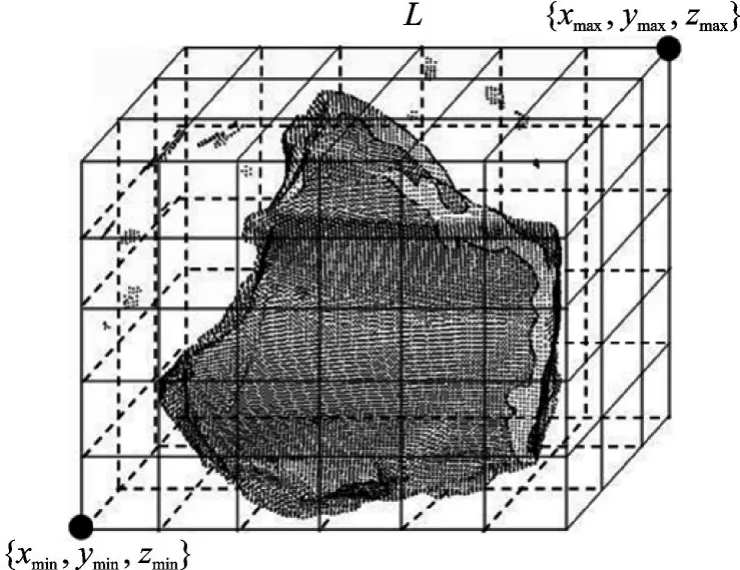
图1 栅格划分示意图Fig.1 Grid division diagram

1.2 大尺度噪声删除

基于以上栅格划分结果，接下来判断每个栅格内的数据点数以删除大尺度噪声，具体步骤如下：

步骤1假设栅格化后点云P的小立方体栅格总数为Sum个，栅格的集合为R={R1,R2,…,RSum}，其中Sum=Sumx×Sumy×Sumz，并定义栅格内点数大于给定阈值的栅格为有点栅格，点数小于等于给定阈值的栅格为无点栅格；

步骤2取第i个小立方体栅格Ri，i=1,2,…,Sum，并判断该栅格内的数据点数，如果Ri为无点栅格，则根据栅格内点的索引号删除Ri内的所有数据点，这些删除的点就是悬浮在点云周围的散乱稀疏的大尺度噪声点；

步骤3如果栅格Ri为有点栅格，则以Ri为中心查看其周围的小立方体栅格内的数据点数；

步骤4继续依次把周围的有点栅格作为中心，查看其周围栅格，直到查看完所有栅格为止，如此就找出了与栅格Ri属于同一片点云的所有相邻栅格；

步骤5取下一个与Ri不属于同一片点云的栅格Rj,j=1,2,…,Sum,j≠i，重复步骤2～4的过程，即可找到与栅格Rj属于同一片点云的所有相邻栅格；

步骤6继续取下一个与Ri和Rj都不属于同一片点云的栅格Rk,k=1,2,…,Sum,k≠j≠i，重复步骤2～4的过程，一直执行，直到将所有栅格都划分到相应的某片点云中为止，如此就将点云P划分成s片点云 {P1,P2,…,Ps}；

步骤7计算每一片点云中有点栅格的数目，从而可以从s片点云中找出含有的有点栅格数目最多的那一片点云，那么该片点云即为主体点云，其余的点云均为距离主体点云中心较远且小而密集的大尺度噪声点，需将其删除掉。

通过以上步骤即可实现点云中的大尺度噪声删除，然后采用特征加权FCM算法删除点云中的小尺度噪声。

2 基于特征加权FCM的小尺度噪声删除

小尺度噪声主要是指混合在主体点云中的噪声点，该噪声的存在会干扰三维模型重建曲面的光滑性，使重建的三维模型存在一定程度的失真。假设删除大尺度噪声后的点云为P′，然后采用特征加权FCM算法对其进行小尺度去噪。该特征加权FCM算法通过在目标函数中引入曲率因子和密度因子来实现点云小尺度噪声的删除。

2.1 FCM算法

FCM算法由Ruspini于1970年首次提出[11]，该算法利用隶属度确定每个数据点属于某个类别的程度。FCM把包含n个l维向量的集合分为m组，每组对应一个聚类中心O={o1,o2,…,om}，计算每个聚类中心oj,j=1,2,…,m，使得目标函数F达到最小。目标函数F的定义式为

式中：U为隶属度矩阵；μij∈U表示每个向量属于各个聚类分组的程度，并且满足；t表示模糊控制参数表示向量和聚类中心oj的Euclid距离，定义式为

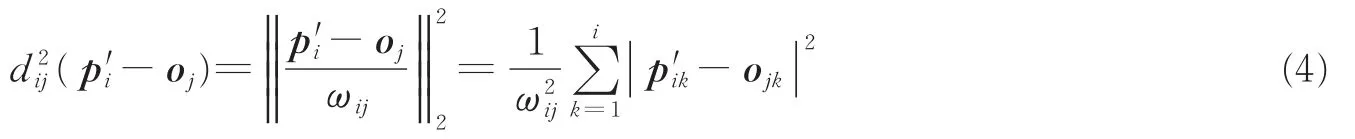
2.2 特征加权FCM算法

特征加权FCM算法通过在FCM算法中加入曲率因子和密度因子实现聚类[12]。对点云P′中的任意一个数据点表示点的三维坐标，定义其 曲率因 子αHi为

式中Hi表示点的平均曲率，1≤i≤n。

平均曲率Hi的定义式为

式中λ0,λ1,λ2表示点的k邻域点集构造的关于点的3×3协方差矩阵C的特征值，并且λ0≤λ1≤λ2，协方差矩阵表示点及其k邻域点的质心。

曲率因子αHi表示点的平均曲率Hi对聚类的影响程度。Hi的值越小，αHi的值也就越小，点pi′包含的特征也就越小；Hi的值越大，αHi的值也就越大，点包含的特征也就越大。

定义密度因子αρi为

式中1≤i≤n。

基于该特征加权FCM算法，对点云P′的小尺度噪声进行删除的具体步骤如下：

步骤1对点云P′中的任意一点采用特征加权FCM算法对其r包围球内的点进行聚类，并统计其r包围球内近邻点的个数，r的取值与栅格划分的数目有关。

步骤2判断点的r包围球内近邻点数目，若大于给定阈值，则将点移动，若小于等于给定阈值，则点p′i为噪声点，将其删除。其中表示聚类中心oj相对于隶属度μij的加权平均值，定义式为

步骤3取下一个未聚类过的点，重复执行步骤1～2，直到点云P′中的所有点都判断完为止，从而实现点云P′的小尺度噪声删除。

3 实验结果与分析

实验硬件环境配置为CPU为Intel(R)Core(TM)i5-4950，主频3.30 GHz,内存为8.00 GB。实验数据采用西北大学可视化技术研究所提供的文物碎片点云数据模型，该数据利用加拿大手持式Handyscan3D激光扫描仪获取，用于实验测试的3个文物碎片点云数据模型如图2所示。

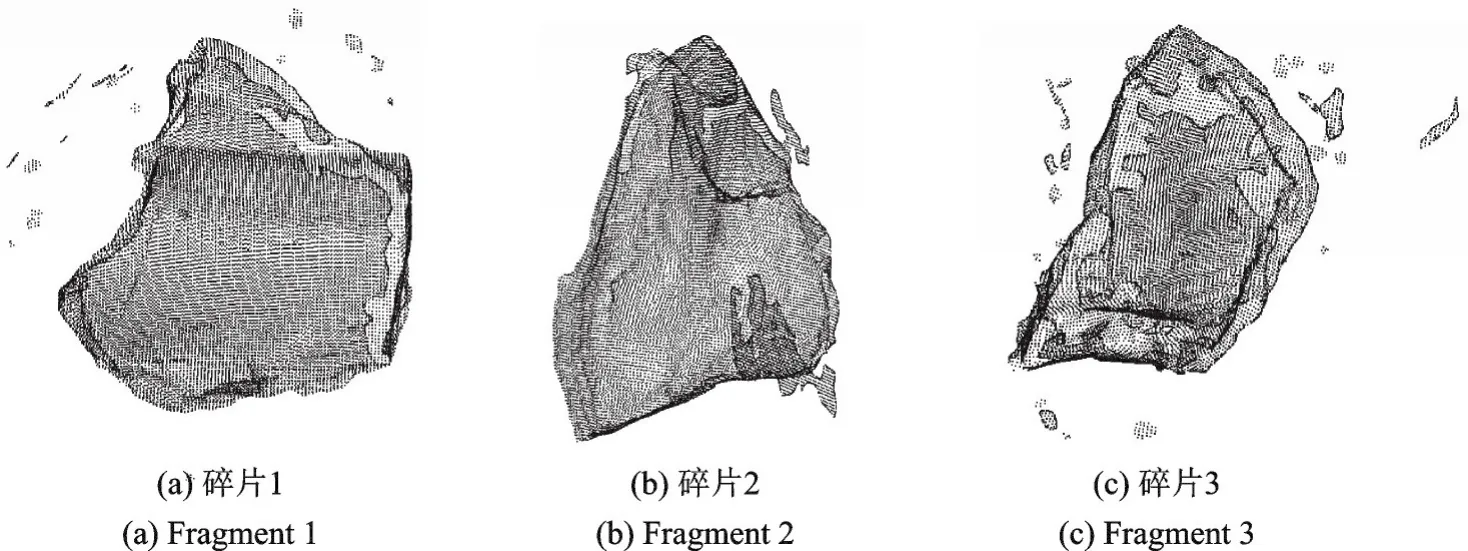
图2 去噪前的文物碎片点云模型Fig.2 Point cloud models of cultural relics fragments before denoising

采用提出的几何特征保持的点云去噪算法，首先通过对点云进行栅格化划分删除大尺度噪声，然后采用特征加权FCM算法删除小尺度噪声，从而实现文物碎片点云的最终去噪。对于图2的文物碎片，分别采用本文提出的该几何特征保持的点云去噪算法、FCM算法[11]、文献[13]算法以及文献[14]算法进行去噪，4种算法对碎片1、碎片2和碎片3的去噪结果分别如图3—5和表1所示。

图3 碎片1的去噪结果Fig.3 Denoising results of fragment 1

图4 碎片2的去噪结果Fig.4 Denoising results of fragment 2

图5 碎片3的去噪结果Fig.5 Denoising results of fragment 3

由图3—5和表1可见，该几何特征保持的去噪算法在有效删除大尺度和小尺度噪声的同时，可以较好地保持文物点云模型的细节特征，具有最低的误差和耗时。与FCM算法相比，本文算法的平均误差降低了约50%，耗时降低了约32%；与文献[13]算法相比，本文算法的平均误差降低了约44%，耗时降低了约25%；与文献[14]算法相比，本文算法的平均误差降低了约34%，耗时降低了约15%。

这是由于FCM算法是一种目标函数基于Euclid距离的模糊聚类算法，对满足正态分布的点云数据具有很好的聚类效果，但是聚类中心的初始化对聚类效果有很大的影响，其时间复杂度为O(nm2)，n表示点云中点的数目，m表示聚类数；文献[13]定义了消除几何不连续点近距离误差和长距离测量误差，实现了点云数据的有效去噪，但是该算法对文物点云的轮廓边缘的保持效果不佳，其时间复杂度为O(n2)；文献[14]是一种基于距离变化、点云强度和密度信息的去噪算法，对密集噪声具有较好的去噪效果，但是对文物碎块点云的离散稀疏噪声删除效果不佳，其时间复杂度为O(nm)；而本文算法采用栅格划分的方式删除大尺度噪声，采用特征加权FCM算法删除小尺度噪声，不仅可以有效剔除悬浮在主体点云周围且偏离主体点云的稀疏点，以及距离主体点云中心较远且小而密集的点，而且对混合在主体点云中的噪声点也有良好的删除效果，其时间复杂度为O(nlog2n)。因此可以证明，本文基于几何特征保持的点云去噪算法是一种更加有效的文物点云模型去噪方法。

表1 不同去噪算法的运行结果Table 1 Running results of different denoising algorithms

4 结束语

针对文物点云数据中复杂噪声难以去除的问题，提出一种保持几何特征的去噪算法。首先通过栅格划分删除大尺度噪声，然后采用特征加权FCM算法删除小尺度噪声，从而达到保留文物点云模型中细节特征的目的。实验通过对文物碎块点云数据去噪来验证所提算法，结果表明本文算法可以在保持文物点云模型的尖锐几何特征的同时，有效删除噪声点，为后期文物的虚拟复原提供了可靠的数据源。但是由于文物碎块点云数据量大小不一，采集环境差异也较大，因此设计通用高效的文物点云去噪算法是下一步研究重点。