基于快速傅里叶变换的降水空间变异函数有效性验证
2020-05-26陈紫阳胡庆芳李伶杰王银堂
陈紫阳,胡庆芳,雍 斌,李伶杰,王银堂
(1.河海大学地球科学与工程学院,江苏 南京 211100;2.南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏 南京 210029)
降水是最基本的气象水文要素之一,受大气运动状态和地理环境因素的共同影响,降水具有复杂的多尺度空间变异性。深入解析降水空间变异性是科学认识降水时空演化规律并定量估计降水空间分布的重要基础[1-3]。降水空间变异性除通过等值线等方式直接展现外,更主要的是采用不均匀指数、空间相关系数、信息熵、经验正交函数分解(empirical or thogonal function, EOF)等统计指标或方法加以分析[4]。如李邦东等[5]采用不均匀指数(变差系数)分析了我国东北地区1961—2010年降水事件,发现在1993年后该地区降水空间不均匀性增加,在一定程度上增加了区域旱涝风险;胡庆芳等[6]采用Moran指数等6种全局或局部空间相关性指标分析了赣江流域降水空间变异性,得出年、月、日降水量整体上呈显著时变空间正相关性,但在局部上具有非平稳性和奇异性的结论;张继国等[7]基于信息熵传输模型,解析了淮河流域年降水在东西方向相关性强、南北方向弱的空间结构特征;徐利岗等[8]基于EOF发现我国北方荒漠区降水总体表现为“相间复杂”和“东西相反”两种空间结构形态;方国华等[9]采用降水质心时间为评价指标,研究了淮河流域降水结构的时空演变规律。
在描述降水空间变异性的众多方法或指标中,空间变异函数(或变方差函数)应用较为广泛[10-12]。空间变异函数的计算方法有两种:传统方法(基于某种理论变异函数的参数拟合方法)和基于快速傅里叶变换(fast Fourier transformation,FFT)的计算方法[13-15]。前者作为传统的计算方法,需要选择特定模型,针对实测数据得到的经验半方差函数进行参数拟合,且一般只能得到特定方向的变异函数值;而后者则不需要进行参数拟合,能够直接提供二维矩阵形式的变异函数计算结果,可以反映任意方向上的降水空间变异性,这是相对传统方法的突出优点。
基于FFT的降水空间变异函数计算方法(以下简称“FFT方法”)在降水空间变异分析和定量估计中已得到应用,如Velasco-Forero等[16]采用FFT方法计算了西班牙Catalonia地区6场降雨的变异函数,并应用于降水空间插值中;Cecinati[17]则将该方法应用于英国雷达-雨量计降水联合估计中。但总的来说,关于该方法的研究仍然很不充分,本文以淮河中上游某区域为例,开展基于FFT方法的有效性研究,并与传统的空间变异函数计算方法进行比较,在不同时间尺度上对FFT方法的有效性加以验证。
1 空间变异函数计算方法
1.1 传统方法
空间变异函数是地质统计学中用于衡量区域化变量在不同位置差异性的统计指标[18-19]。对于区域化变量Z(xi)和某一空间分离距离h,若Z(xi)均值存在且不取决于空间位置xi,同时对于任意xi和h,Z(xi+h)-Z(xi)的方差存在,且不取决于xi,则Z(xi)的空间变异函数可表达为
γ(h)=V[Z(xi+h)-Z(xi)]/2=
E{[Z(xi+h)-Z(xi)]2}/2
(1)
式中:V为方差;E为均值。显然,若Z(xi)呈空间正相关,则|h|越大,变异函数值γ(h)越大;反之,γ(h)越小。在Z(xi)满足二阶平稳条件的情况下,变异函数与协方差函数以及空间相关系数存在以下转换关系:
γ(h)=σ2-C(h)=σ2[1-ρ(h)]
(2)
式中:C(h)为协方差函数;ρ(h)为空间自相关系数;σ2为方差。
传统的空间变异函数计算主要包括以下两个步骤:
a. 根据分离距离为h的样本数据对,采用下式计算经验变异函数值:
(3)
式中Ph为分离距离为h的样本数据对的数量。
b. 选择满足正定性要求的有效变异函数模型对经验变异函数值进行参数拟合,得到理论变异函数。常用的理论变异函数模型主要有球状模型、指数模型和高斯模型等。以高斯模型为例,其对应的变异函数表达式为
γ(h)=C0+C1[1-e-(h/a)2]
(4)
式中:a为变程,反映区域化变量的相关尺度;C0为块金值,反映极短分离距离之间变异函数的不连续性;C1为变异系数,反映区域化变量变化速率的大小。a、C0、C1为高斯模型的参数。
由于区域化变量在不同方向可能会具有不同的结构性和变异性(即空间各向异性),故为全面了解区域化变量的空间分布特性,需要对不同方向分别计算空间变异函数,同时还需要根据各向异性的具体性质,对不同方向上的变异函数进行拟合,这正是采用传统方法较为麻烦之处。
1.2 FFT方法
与传统方法不同,FFT方法不需要针对各个方向采用特定模型对经验变异函数值进行拟合,它是一种非参数计算方法。这种方法首先计算出区域化变量的协方差矩阵,然后用FFT将协方差矩阵转换到频域进行处理,最后再通过快速傅里叶逆变换(inverse fast Fourier transform,IFFT)将协方差函数变换回时域,最后利用变异函数和协方差函数之间的转换关系得到二维矩阵形式的空间变异函数。
FFT方法的具体步骤如下:
a. 首先根据样本数据的空间分布特征,将研究区域划分成一系列矩形格网,格网横向和纵向的分辨率分别为x、y。各格网中区域化变量的数值为分布在格网中的采样点的均值,分离距离h=(mx,ny)(m、n为格网相对平移行列数,m、n可为负数)。为方便计算,格网行列数m、n取2k+1(k>2)。
b. 采用下式计算分离距离h对应的协方差函数值C(h):


(5)
由于采样点数量有限,因此并非研究区域内的所有格网均是有数据的,这导致可能没有样本数据对用于计算某些h对应的协方差函数值,因此在用FFT进行变换之前要将协方差函数进行初步插值,本文采用下式进行计算:
(6)
其中
式中:Cmn为待插值点的协方差值;m、n为所在行列数;P为参与插值的点的数量;λi为插值权重;Ci为插值点的协方差值;pi为计算相应格网协方差函数值所采用的样本数据对数量;di为插值格网与待插值格网间的距离。由于区域化变量常具有各向异性,因此在对协方差函数插值时需要考虑方向。首先连接中心点与待插值格网,然后在其连线左右一定容差角度范围内,筛选出与待插值格网相距较近的插值点,最后根据这些距离待插值点较近点的协方差函数值即可拟合出待插值格网的协方差函数值。
c. 采用下式所示的FFT将协方差矩阵从时域转换到频域:

(7)
式中:M、N为协方差矩阵的行数和列数;Smn为频域中第m行、第n列的频谱值。为保证正定性条件,采用式(7)获得频谱图后需要用式(8)所示的移动窗口平滑算法对各个频谱值进行优化,逐步加大窗口宽度直到每个频谱值为非负。如果窗口太大而频谱值仍然为负,则可以直接将所有频谱值加上所有值中最小值的绝对值(最小值太小会使整个频谱基数变大从而使最终的变异函数变化平缓)或者直接将此结果设置为0来进行校正。
(8)

d. 采用式(9)的IFFT将Smn转换回时域,在协方差函数矩阵的基础上,根据式(2)得到优化后的变异函数矩阵。
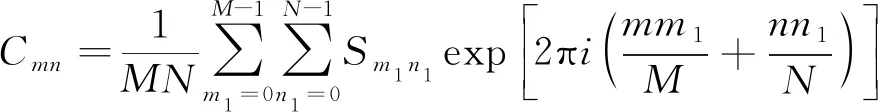
(9)
2 研究区域与数据
选择淮河流域中上游一长宽均为170 km的方形研究区域(图1)来验证FFT方法计算结果的合理性。研究区域位于安徽省阜阳附近(东经115°10′~116°51′,北纬32°8′~33°41′),地跨淮河干流两岸,属于我国南北过渡带,高程介于-11~409 m,多年平均降水量为900~1 000 mm。
研究区域内共有雨量站127个,面积约28 900 km2,站点密度约为230 km2一个。研究数据为从《淮河流域水文年鉴》中收集的127个站点2010—2015年连续的年、月、日降水数据,降水数据经过了严格的质量控制。
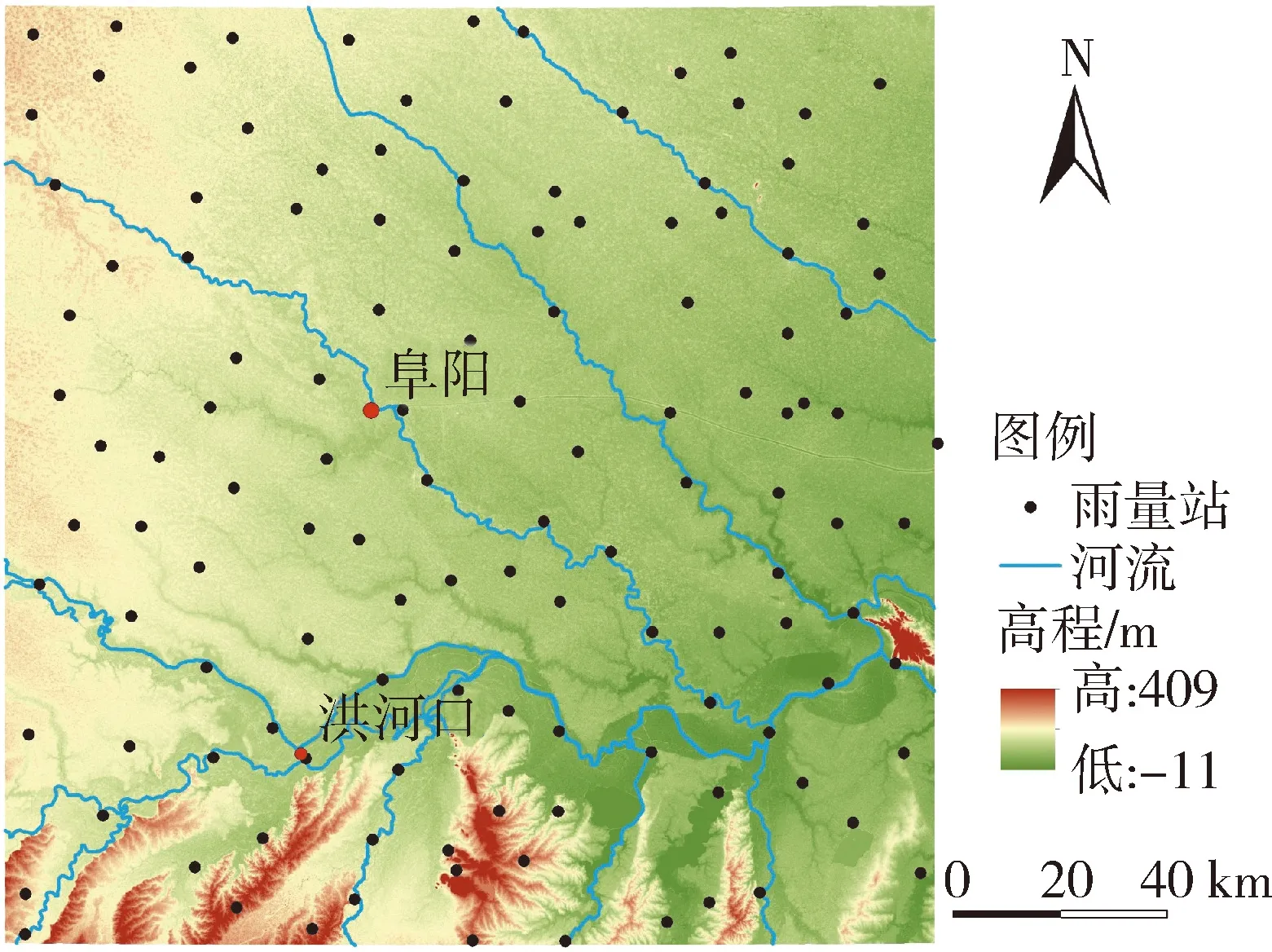
图1 研究区域与雨量站点分布
3 结果分析与讨论
根据研究区域内2010—2015年的降水数据,采用FFT方法计算了年、月、日3种时间尺度上的降水空间变异函数,从东-西(E-W)、东南-西北(SE-NW)、南-北(S-N)、西南-东北(SW-NE)4个方向比较了FFT方法与传统方法的差异。
3.1 年降水量空间变异函数
图2为FFT方法计算得到的研究区域年降水量(2012年)的空间变异函数(为二维矩阵,图中每个像元的大小为10 km×10 km,图像大小为 330 km×330 km,以向E、N为正,向W、S为负,图像中心处表示分离距离为0的变异函数值,其他各位置表示不同分离距离和方向上的变异函数值)。显然,空间变异函数矩阵具有中心对称性,研究区域年降水量在空间上呈现出不同程度、不同特点的带状各向异性。对于2012年年降水量,其在SE-NW方向空间变异较快,而在SW-NE方向的变异相对较慢。从图2还可发现,变异函数的块金值约为 1 800 mm2,基台值大致为18 000 mm2,变程为80 km。在变程范围内,年降水量是结构性和随机性的统一体。随着分离距离的不断增加,年降水量的空间结构性逐步降低、随机性不断增强。

图2 FFT方法计算的年降水量空间变异函数
图3为两种方法计算的年降水量(2012年)空间变异函数对比(为对比两种方法的差异性,图中也给出了采用经验变异函数直接计算得到的散点值),其中传统方法采用了多种模型进行拟合,最终选取了拟合效果最好的球形模型。总体而言,传统方法计算结果与经验变异函数计算值更为接近,且传统方法和FFT方法所得结果在多数情况下具有相近变化特征,如E-W方向两种方法所得年降水量空间变异函数值就很接近。


(a) E-W
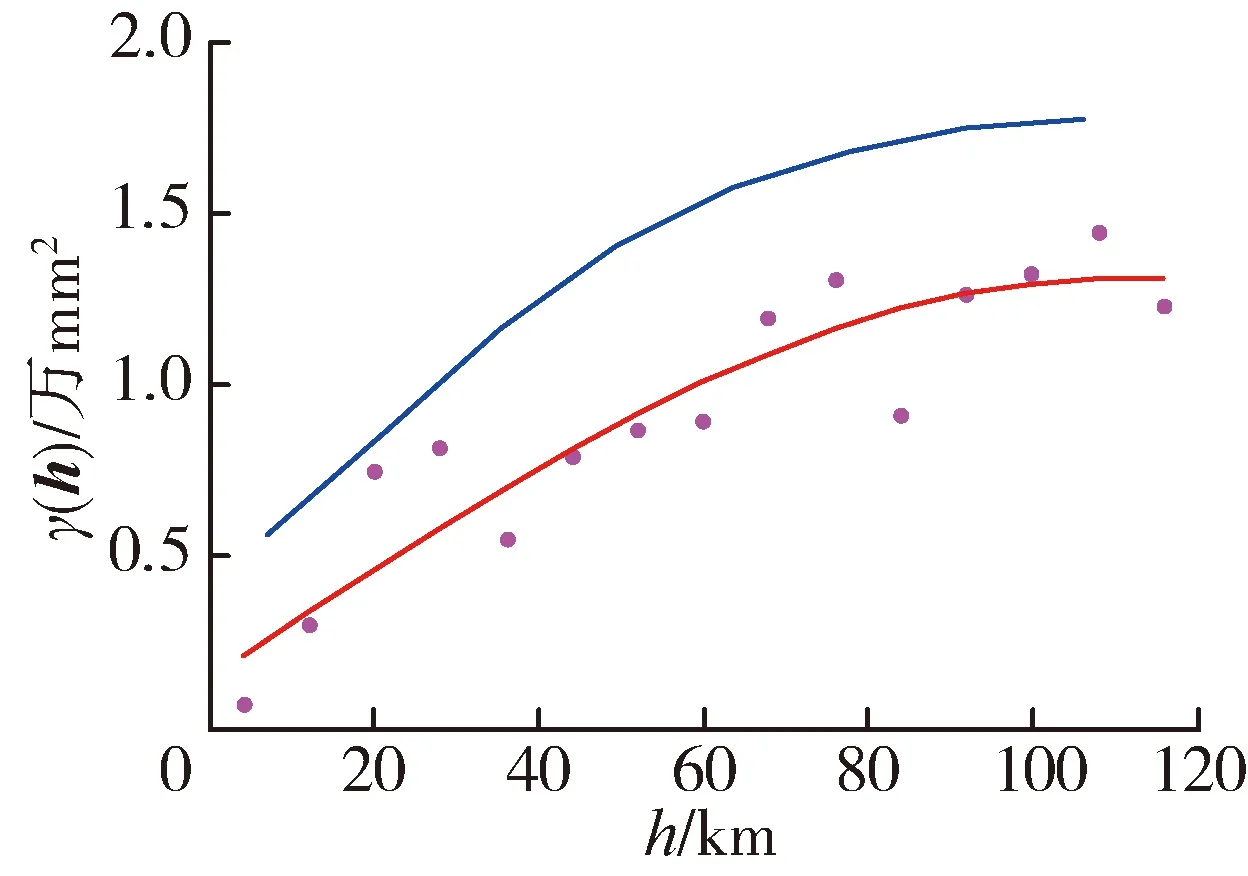
(b) SE-NW

(c) S-N
(d) SW-NE
3.2 月降水量空间变异函数
图4为FFT方法计算的月降水量(2012年9月)空间变异函数。由图4可知,研究区域内月降水量的空间带状各向异性特征也很明显。月降水量在E-W和S-N方向变化慢,在SE-NW和SW-NE方向变化慢。从图4还可以看出月降水量空间变异函数的块金值约为100 mm2,基台值大致为1 800 mm2,S-N方向变程约为100 km,E-W方向变程约为 80 km。与年降水量相似,随着分离距离的增加,月降水量的半方差函数值不断增大,随机性不断增强;直至分离距离达到和超过变程后,月降水量的半方差函数值趋于方差值。

图4 FFT方法计算的月降水量空间变异函数
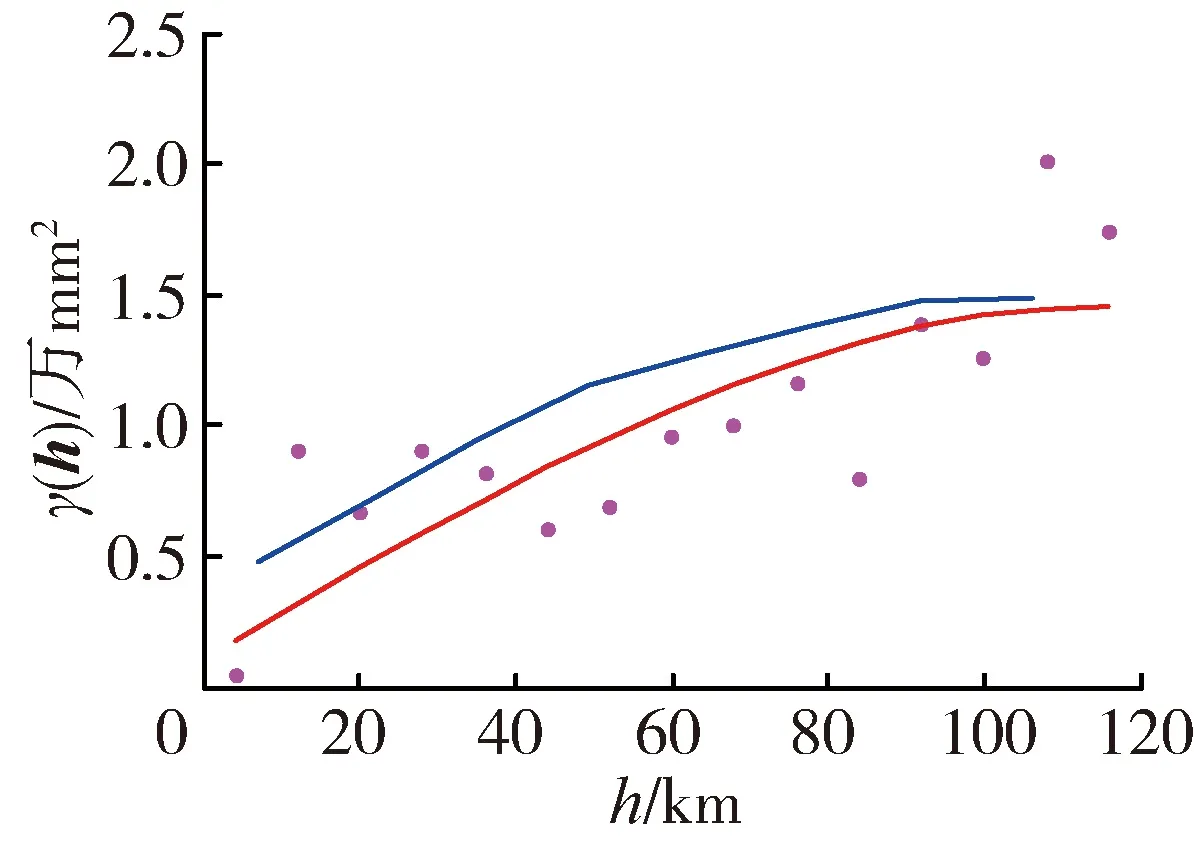
图5为两种方法计算的月降水量(2012年9月)空间变异函数对比,其中传统方法选取了拟合效果最好的高斯模型。总体而言,其规律与年降水量类似,传统拟合方法计算结果与经验变异函数计算值更为接近,但传统方法和FFT方法所得结果在多数情况下具有相近的变化特征。
3.3 日降水量空间变异函数
图6为FFT方法计算的日降水量(2015年6月25日)空间变异函数。由图6可知,日降水量在S-N方向变异较慢,E-W方向变异快,但即便如此仍有一定差异。日降水量空间变异函数的块金值约为 2 mm2,基台值大致为50 mm2,S-N方向变程约为110 km,E-W方向变程约为80 km。
图7给出了两种方法计算的日降水量(2015年6月25日)空间变异函数值对比,其中传统方法选取了拟合效果最好的指数模型。FFT方法所得日降水量空间变异函数在长距离上的表现没有传统方法效果好,但在短距离上两者所得结果较为接近。
4 结 语
本文在介绍空间变异函数计算方法的基础上,以淮河中上游某区域为例,通过与传统方法的比较,在年、月、日时间尺度上对FFT方法的计算结果进行了验证。在年、月时间尺度上,FFT方法和传统方法所得降水空间变异函数具有相近变化特征,而在日时间尺度上,两者在短距离上所得结果也较为接近。


(a) E-W

(b) SE-NW

(c) S-N

(d) SW-NE

图6 FFT方法计算的日降水量空间变异函数
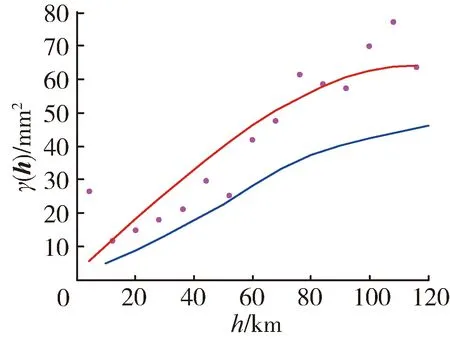
(a) E-W
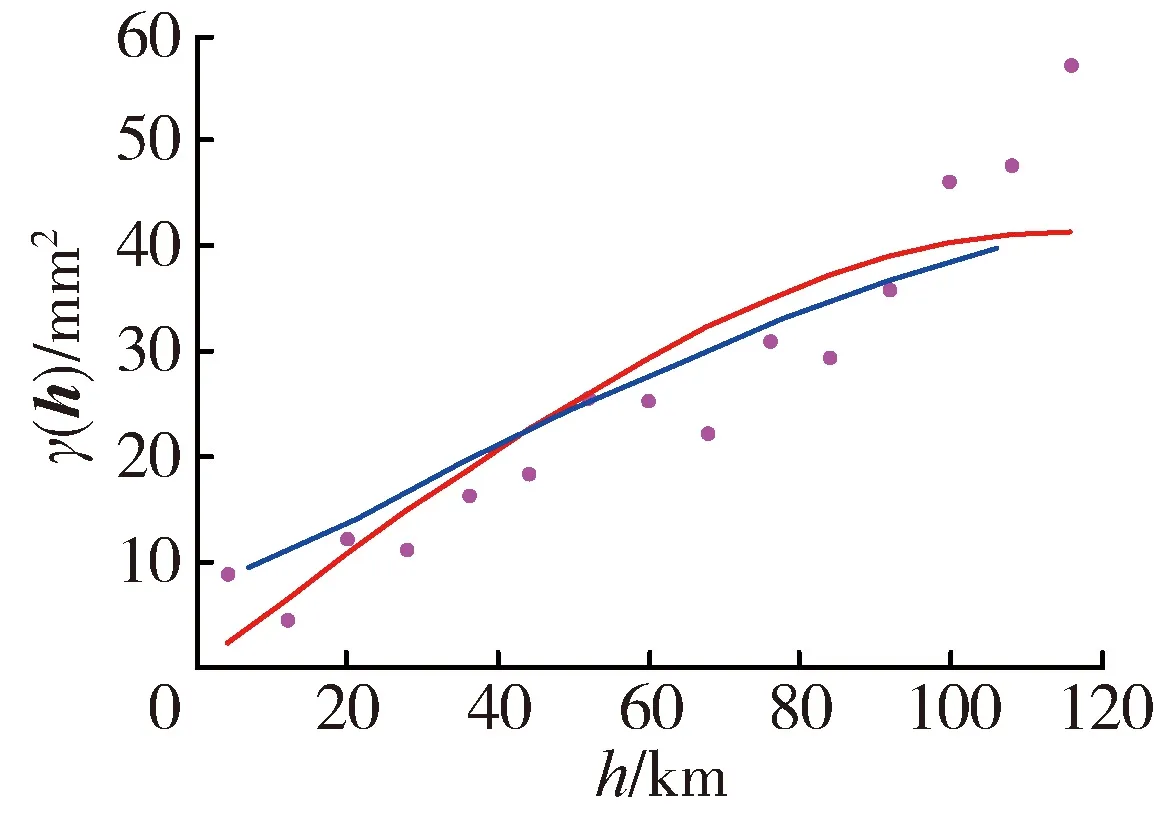
(b) SE-NW

(c) S-N

(d) SW-NE
本文的研究证实了FFT方法在细致解析降水空间结构特征上的价值,下一步将运用该方法开展降水空间定量估计的研究,并比较不同降水空间变异函数计算方法对降水定量估计结果的影响。
