不同降雨条件下不稳定斜坡财产损失风险评价——以镇巴县兴隆镇为例*

宋宇飞 范 文 李 军 杜 珣

(长安大学地质工程与测绘学院， 西安 710054， 中国)

0 引 言

秦巴山区地质构造复杂，岩性种类多，分布范围广(Mattauer et al.，1985),由变质岩风化形成的碎石土堆积层成为区内滑坡主要的孕育场所之一(Fan et al.，2019)，碎石土大孔隙的性质决定了区内滑坡受降雨、地下水位等因素变化的影响强烈(许建聪等， 2008)，以瓦房店幅(地理坐标：E 108°15′～108°30′，N 32°30′～32°40′)为例，图幅面积400ikm2，自2000年起新发生浅表层滑坡163起，其中由降雨诱发156起，由2010年7月18日特大降雨诱发119起，可见区内降雨对浅表层滑坡的发生起决定性的作用(Fan et al.， 2017)。

根据调查资料，瓦房店幅2000年后发生的163起浅表层滑坡中，79起有切坡现象，这些灾害广泛分布于研究区内，并在人类活动频繁的城镇周围集中，严重威胁着人民生命财产的安全，采取有效、合理、经济的安全防治措施对城镇的安全性至关重要，而不稳定斜坡财产损失风险评价是安全防治措施的基础(Guzzetti et al.，1999； Chau et al.，2004； Cascini， 2008; 吴越等， 2010)。

风险一词由来已久，国内外的不同学者提出过多种不同的风险定义，如1984年美国滑坡专家Vanes(1984)提出地质灾害风险由地质灾害发生破坏的可能性和产生的后果两方面构成; 1992年联合国正式给出地质灾害风险的定义(UNDHA， 1992)：“地质灾害风险是在一定区域、一定时间段内，由某一地质灾害而引起的人们生命财产和经济活动的期望损失值”； 2001年中国学者戴福初(Dai et al.，2001)对滑坡风险评估和管理的框架进行了论述，指出滑坡风险是由滑坡的发生概率、滑坡的运动行为以及承灾体的易损程度构成； Fell等在2005年(Fell et al.，2005)提出的风险计算的量化公式(文献中式4.1)，得到了广大学者的认可； 向喜琼等(2000)基于地理信息系统论述了灾害风险评价和风险管理的流程，提出区域地质灾害风险评估的构想； 吴树仁等(2009)，吴树仁(2012)对地质灾害风险评估的方法与制图分级的原则作了完整的概括。

风险评价针对不同研究区的范围大小、数据详实程度、期望的输出精度等可以分为定量和定性两种方式(Dai et al.，2001)，由于本研究区面积较小，调查资料充足，故本文采用逐坡定量的评价方式，根据Fell提出的公式(4.1)(Fell et al., 2005)，定量评估需要确定滑坡的发生概率、滑体的运动特性(空间概率)以及受灾体的易损性和价值。不同的学者提出过多种不同的方法来确定这几个分量，如唐亚明(2008)采用统计矩、一次二阶矩、几何法以及蒙特-卡洛对边坡的破坏概率进行了计算，并对比了不同方法之间的优缺点； 魏婷婷等(2017)以斜坡单元为计算单位，利用FLAC(2D)命令流文件，自动逐坡的计算得到了大范围区域斜坡稳定性系数分布图； 吴越(2011)从滑坡运动速度和能量的角度探讨了不同滑坡作用下，建筑物的易损性值的变化情况； Negulescu et al.(2010)采用数值的方法分析了承灾体的破坏程度与地表位移的关系； 许强等(2010), 刘艳辉等(2018)针对山区城镇的特点，建立了一套适合山区城镇承灾体的易损性评价体系； 薛强等(2018)以斜坡单元为评价单位，针对斜坡在不同含水量工况下的稳定性问题，采用模拟与监测并行的手段，对绥德县城进行了风险评价。

本文以兴隆镇为例，为探索降雨强度对不稳定斜坡财产损失风险的影响，收集了研究区近60年日值降雨数据集，通过P-Ⅲ型曲线拟合得到不同重现期下的强度，通过饱和入渗公式将降雨工况和斜坡破坏概率联系起来，通过野外调查与大比例尺的建筑测绘，对建筑的易损性和价值做了准确的评估，计算得到的不同降雨工况下的斜坡财产损失风险可以满足不同级别的防治需要。

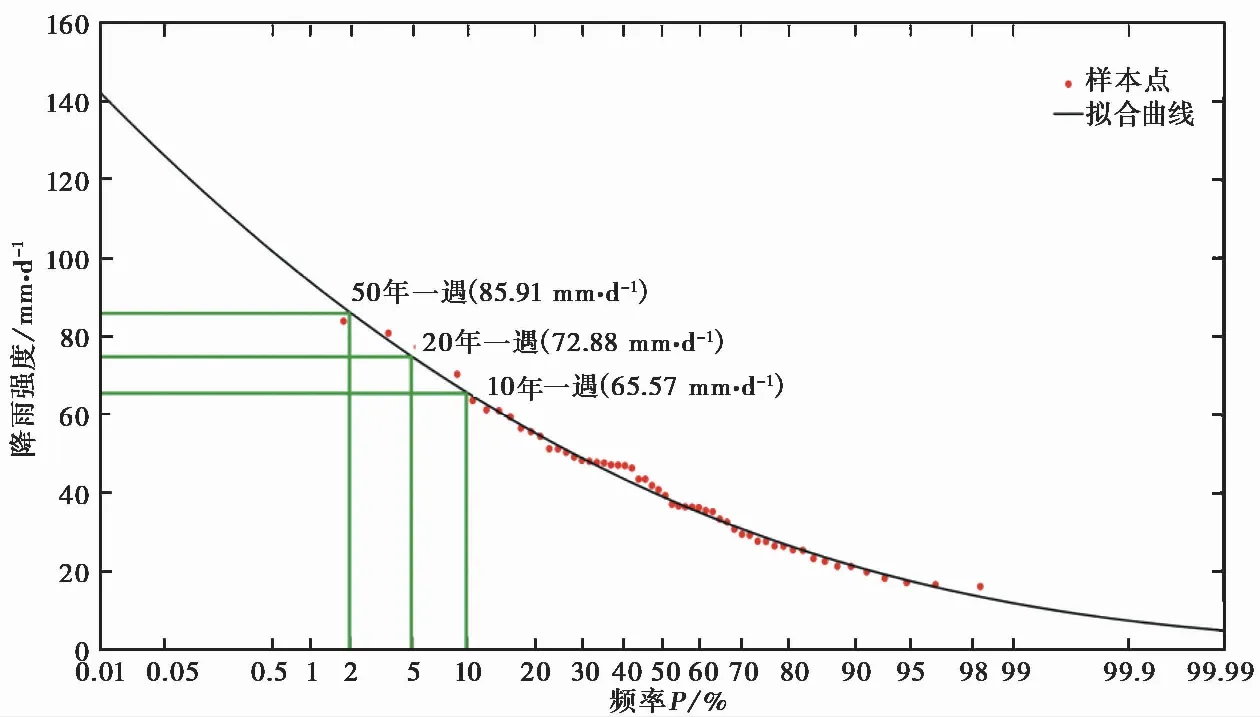
图 1 理论降雨强度-重现期分布曲线Fig. 1 Curve of rainfall intensity and recurrence period

1 研究区概况

兴隆镇位于汉中市镇巴县境内，地处秦巴山区腹地，城镇四周环山，海拔介于650～882im之间。城镇及周边地层以寒武系的褐黄色薄层粉砂岩、碳质粉砂岩、条带状灰岩为主，原岩倾角73°～80°、倾向265°～290°，褐黄色薄层粉砂岩易发生弯折破坏进而风化形成碎石土覆盖层，由于岩性较软，堆积层较厚(3～5im)，隐患斜坡多集中在这一层。

境内年平均降雨量为1309imm，年内降雨分布极不均匀，集中在夏秋两季，约占全年总降雨量的80%，降雨最多的月份为7月，平均降雨量达到292imm。区内降雨常为暴雨、连阴雨。风化堆积层的大孔隙特性决定了斜坡易受降雨的影响发生滑坡，且常为浅表层滑坡，城镇周边斜坡的风化堆积层的饱和渗透系数约为0.416×10-3cm·s-1，孔隙率可达0.44，雨水容易沿着大孔隙快速到达土岩接触面，从而发生滑坡。

2 降雨概率及入渗深度

根据《重点集镇地质灾害勘查规范》的推荐，降雨条件选择10年、20年、50年一遇降雨，降雨时长为5日，通过拟合该地区历年的极值降雨样本点，求得各工况下的降雨强度，之后通过饱和入渗公式求取不同工况下的降雨入渗深度。

2.1 数据来源

降雨数据： 1959年1月1日到2015年12月31日的日值降雨数据集(镇巴县气象站)； 地形数据： 1︰1000 高精度DEM数据，用于斜坡单元划分、斜坡剖面提取、坡度计算等； 地质图数据： 1︰250000 安康市幅地质图； 野外调查数据：城镇周边29个斜坡的覆盖层厚度、斜坡范围、信手剖面图等； 测绘数据： 1︰1000 的城镇房屋测绘数据，以及后期关于房屋结构、类型、使用年限等的调查数据

2.2 降雨强度

为了得到某一重现期下的降雨强度，需要对以往降雨数据进行统计分析，本文收集的数据是镇巴县降雨站(站号： 57238)自1959年1月1日到2015年12月31日的每日降雨值，采用年最大值法采样，共选取57组样本点进行统计分析，目前我国水文计算规范推荐水文变量统一服从P-Ⅲ型分布(黄振平， 2003)，理论降雨强度由式(1)求取：

(1)

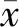
表 1 5日累计降雨量极值分布的参数估计Table 1 Parameters of accumulative rainfall peak distribution curve under 5 days continuous rainfall

表 2 不同降雨历时和重现期下的降雨强度(单位： mm·d-1)Table 2 Rainfall intensity under different rainfall durations and recurrence periods

2.3 降雨入渗深度

本文假定所有斜坡的破坏方式均为浅表层滑动，故在计算降雨入渗深度之前，首先要对不稳定斜坡的上覆土层的厚度进行调查，为了计算的准确性，厚度调查点沿剖面线的方向进行布置，以获取较为准确的计算剖面图，本次调查斜坡29个，厚度点共64个(图 2)。

图 2 兴隆镇周边斜坡土层厚度调查点Fig. 2 Thickness point of slope soil around Xinglong town

兴隆镇斜坡碎石土的饱和渗透系数平均为0.416×10-3cm·s-1，当降雨强度小于饱和渗透系数时，斜坡不会发生积水(Beven et al.，2004)，兴隆镇周边斜坡可以接受359.4imm·d-1的降雨而不发生积水，故可以采用Green-Ampt模型中的非积水入渗部分进行入渗深度的计算(李宁等， 2012)，计算公式如下：

y=t·q·cos(α)/(Qs-Qi)

(2)

式中，y为入渗深度；t为降雨时间，取5日；q为降雨强度，取表 2中数值，α为斜坡坡度，可根据计算剖面确定，Qs为饱和含水率，Qi为初始含水率，分别取25.51%和15.59%。

3 财产风险评价

针对秦巴山区浅表层滑坡的多发性和其受降雨影响的敏感性，以镇巴县兴隆镇为例，对城镇周边有隐患的斜坡进行不同降雨工况的风险评价，评价的过程中假定隐患斜坡可能发生的破坏形式均为浅表层破坏，以斜坡的破坏概率作为危险性的表达形式，承灾体为隐患斜坡影响范围内的建筑物，最后对各不稳定斜坡进行定量的财产损失计算。

3.1 评价方法

滑坡财产损失风险是指未来潜在滑坡灾害发生所造成财产损失的期望值，对于本文所采用的单体滑坡财产风险评价而言，采用前述的Fell在2005年提出的定量风险计算公式，如下：

R=P(H)·P(T|H)·P(S|T)·V(P|S)·E

(3)

式中，R为年财产损失风险(元/年)；P(H)为斜坡的破坏概率，取值0～1；P(T|H)为不稳定斜坡与承灾体的空间概率，也称到达概率；P(S|T)为不稳定斜坡与承灾体的时间概率，对于建筑物这种固定的承灾体，若其处于斜坡的影响范围内，则取值为1，否则为0；V(P|S)为承灾体的易损性，为0～1之间的无量纲数；E为承灾体的价值。

3.2 斜坡破坏概率计算

斜坡破坏概率计算分4种工况：天然状态、10年一遇5日、20年一遇5日、50年一遇5日，斜坡原始剖面按实际情况分为2或3层，分别为上覆碎石土层、强风化粉砂岩、基岩，在接受降雨后，根据式(2)计算得到的降雨入渗深度，在模型中增加一层饱和碎石土层，同一斜坡接受不同的降雨强度所对应的饱和碎石土层的深度不同，采用的计算模型也不相同，模型的材料参数可见表3。

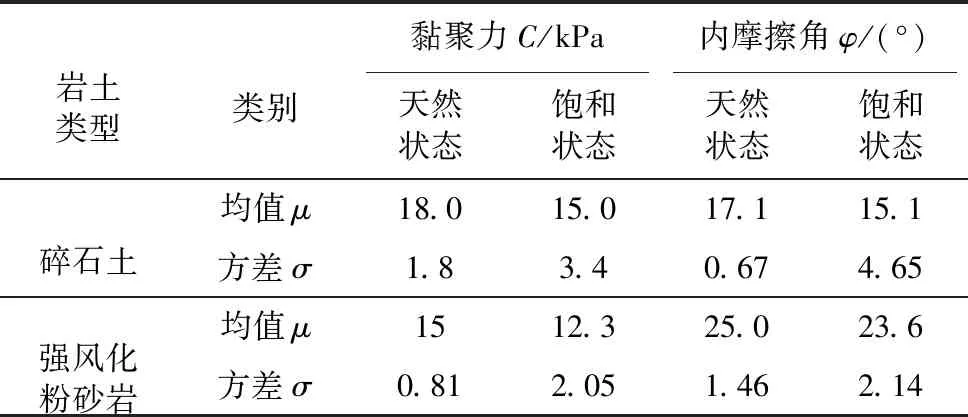
表 3 兴隆镇周边斜坡岩土体物理力学参数表Table 3 Physical-mechanical parameters of soil on slope around Xinglong town

破坏概率的计算采用蒙特-卡洛法，斜坡稳定性状态函数采用Bishop函数，认为稳定性状态函数中的C、φ为相互独立的服从正态分布的随机变量，其余参数为定值(罗冲等， 2005)，本文以2-6号斜坡为例对计算过程进行说明， 2-6号斜坡曾有过滑动记录，坡高80im，平面上呈圈椅状，钻孔资料显示，坡体上层为碎石土层，平均厚度为9.3im，中层为强风化粉砂岩，平均厚度为7.6im，底层为灰岩， 2-6号斜坡的剖面图见图 3。

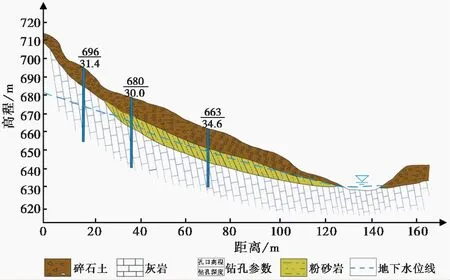
图 3 斜坡2-6工程地质剖面图Fig. 3 Profile of slope 2-6

利用Geo-slope软件对4种工况下斜坡的剖面进行抽样10i000次的安全系数计算，从而可以得到斜坡在不同降雨条件下的安全系数分布形式，考虑Fs<1为失稳，Fs≥1为稳定，则破坏概率P可近似为M/N，其中，M为N次试验中安全系数小于1的次数，N为总的试验次数，这里取10i000， 2-6号斜坡在不同降雨条件下的计算模型及得到的安全系数分布可见图 4，图 5，为节省篇幅这里只列出天然与20年一遇降雨两种工况的计算模型及结果。城镇各斜坡在不同降雨条件下的破坏概率分布可见图 6。

3.3 建筑物易损性分析

易损性的评价取决灾害的强度和承灾体的脆弱性两方面(式(3))，根据文献(杜娟， 2012)中的评价方法，从滑坡冲击力和滑体厚度两方面评价不稳定斜坡破坏时的作用强度，从建筑物的结构类型、维护状况、使用年限以及水平承载力4个方面来评价房屋的脆弱性。

(4)

式中，V为承灾体的易损性；I为滑坡作用强度；S为承灾体的脆弱性(抗灾能力)。

3.3.1 滑坡作用强度

滑坡的作用强度I计算公式如下(杜娟， 2012)：

I=1-(1-Ipre)·(1-If-dep)

(5)

式中，Ipre为滑坡冲击力强度指标，是由滑坡冲击力与建筑物水平方向极限承载力的比值根据表 4取值，其中，滑坡冲击力可以通过Valentine(1998)提出运动滑体冲击强度公式进行计算：

(6)

式中，P为运动滑体的冲击力(kPa)；ρ为滑体密度(kg·m-3)；v为滑速(m·s-1)。而建筑物水平方向极限承载力根据建筑物的结构状况从表 5中取值。

表 4 滑坡冲击力强度指标的取值Table 4 Landslide impact strength index

表 5 建筑物的水平极限抵抗力Table 5 Horizontal resistance of buildings

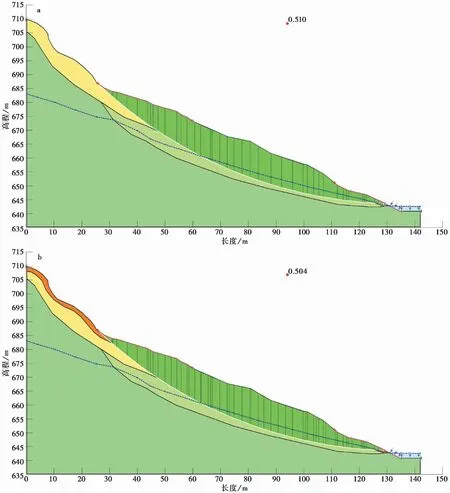
图 4 斜坡2-6在不同降雨条件下的计算模型Fig. 4 The model of slope 2-6 under different rainfall conditionsa. 天然状态计算模型； b. 20年一遇降雨计算模型

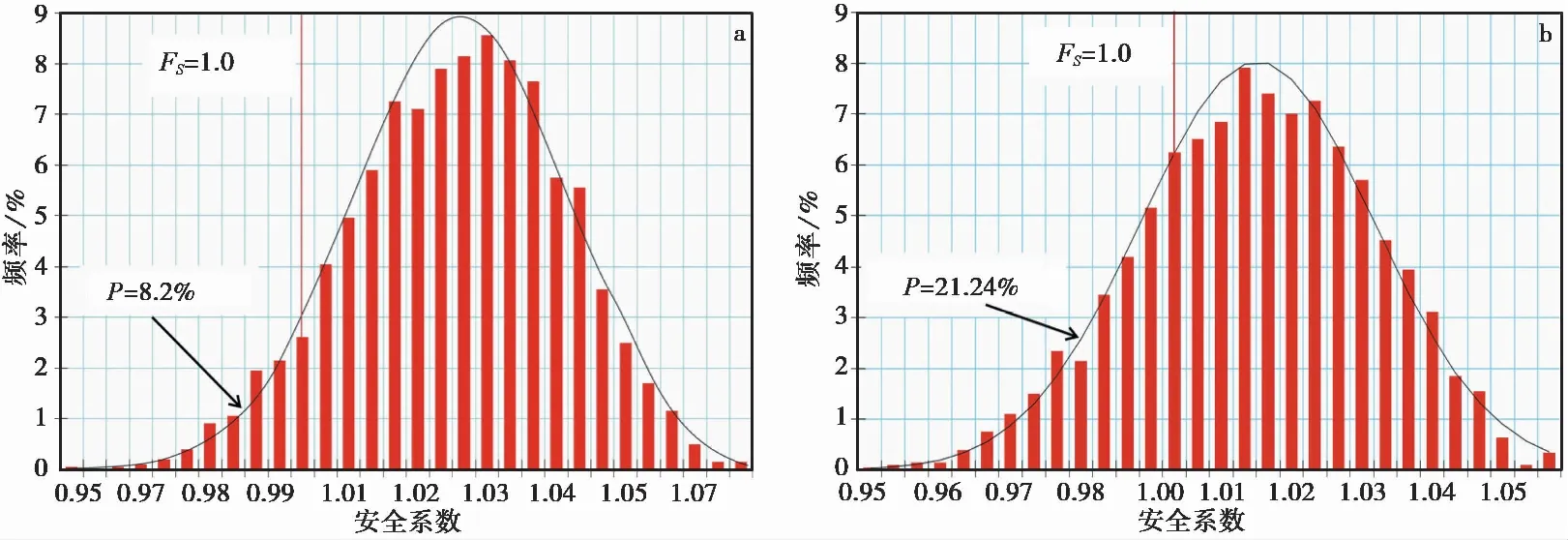
图 5 斜坡2-6在不同降雨条件下的安全系数分布情况Fig. 5 The safety factor distribution of slope 2-6 under different rainfall conditionsa. 天然状态安全系数分布； b. 20年一遇降雨安全系数分布

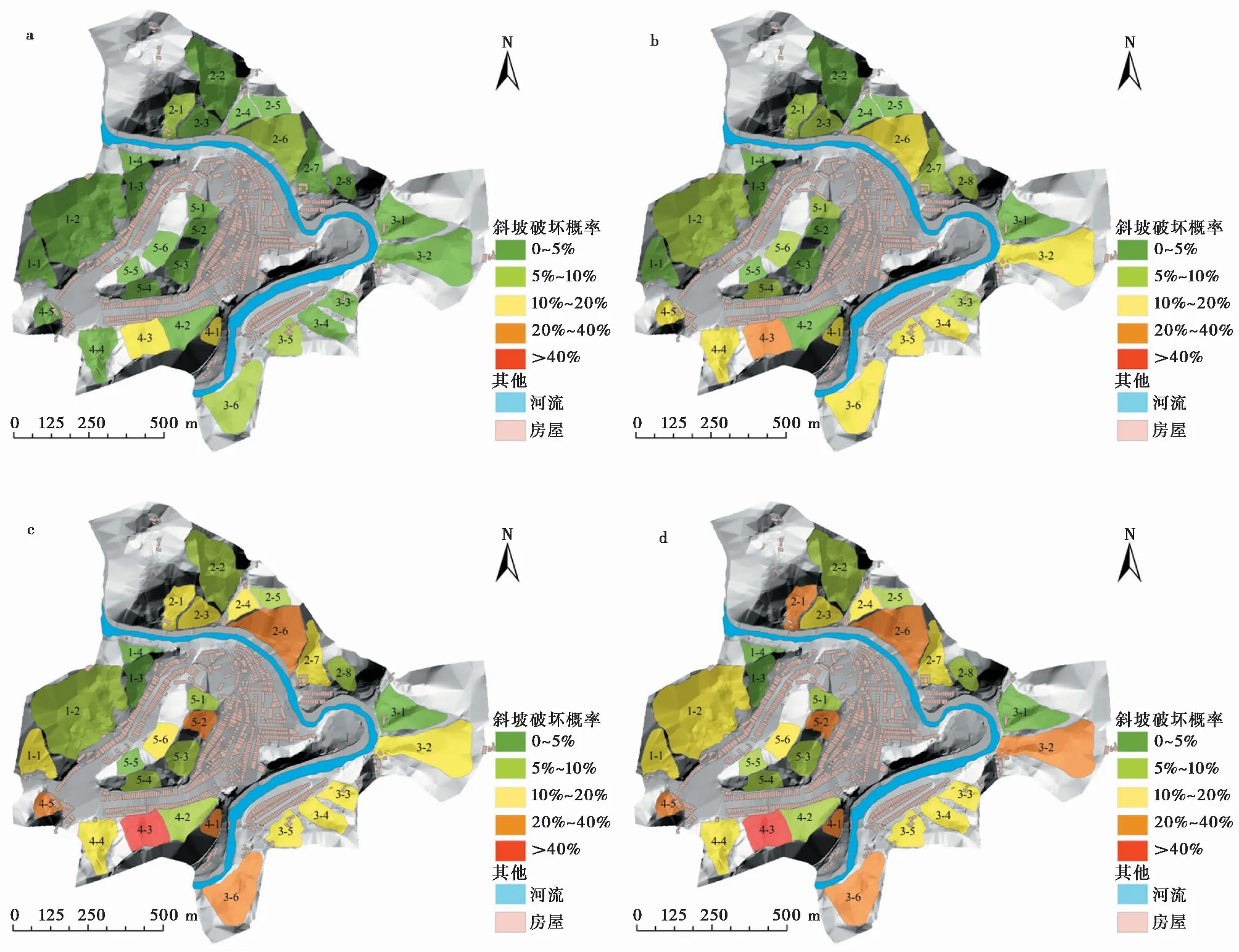
图 6 斜坡在不同降雨工况下的破坏概率Fig. 6 Failure probability of slopes under different rainfall conditionsa. 天然状态； b. 10年一遇； c. 20年一遇； d. 50年一遇

If-dep为运动滑体深度强度指标，通过滑体深度与建筑物高度的比值按照表 6取值。

表 6 运动滑体深度强度指标的取值Table 6 Index of landslide mass depth

表 7 建筑结构类型脆弱性指标取值Table 7 The vulnerability index of building structure

3.3.2 承灾体的脆弱性

承灾体的脆弱性按照式(7)计算：

S=1-(1-Sstr) · (1-Smat) · (1-Sser)

(7)

式中，Sstr为建筑物的结构类型指标，按表 7取值；Smat为建筑物的维护状况指标，按表 8取值；Sser为建筑物的使用年限指标，按表 9取值。

在得到房屋的脆弱性和不稳定斜坡的作用强度后，由式(4)可以得到房屋的易损性分布图(图 7)。

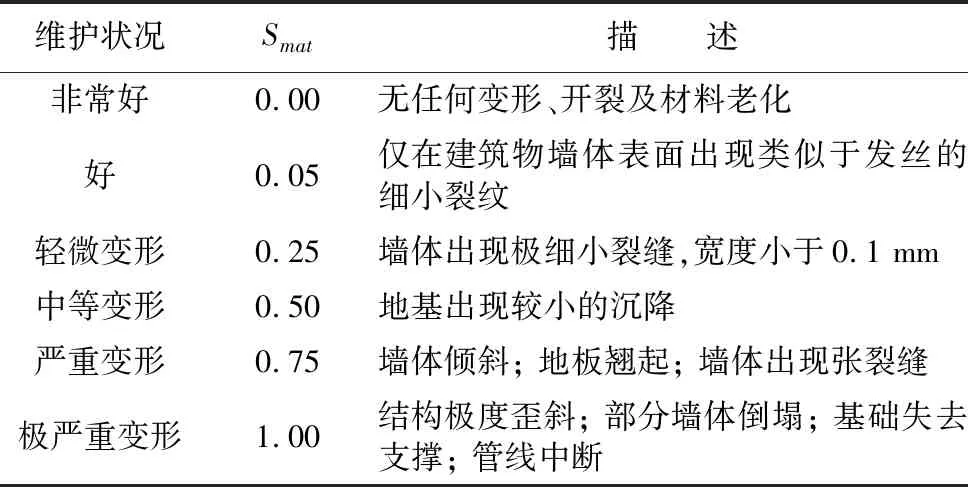
表 8 建筑物在不同维护状况下的脆弱性指标Table 8 Vulnerability index of buildings under different maintenance conditions

表 9 建筑物使用年限脆弱性指标取值Table 9 Vulnerability index of building service life

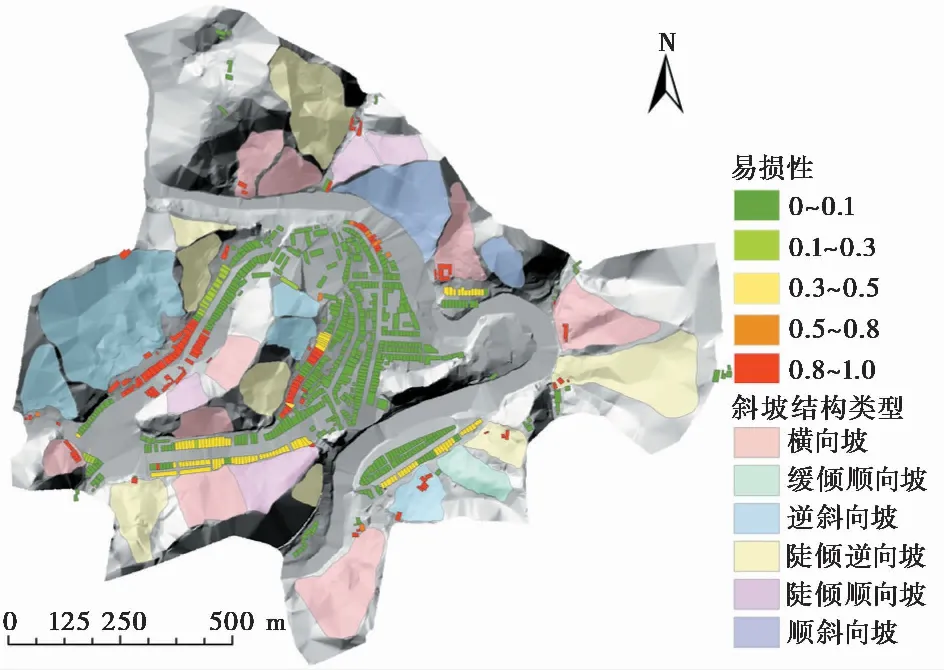
图 7 房屋易损性值分布图Fig. 7 Vulnerability of house

3.4 斜坡与承灾体的时空关系

由于本文的承灾体固定不动，所以对于斜坡影响范围内的承灾体，当灾害发生时必然会受到影响，其时间概率和空间概率为1，而对于影响范围外的承灾体，无论灾害发生与否都不会受到影响，故其时间概率和空间概率为0。

3.5 承灾体价值

根据野外实地调查，选取房屋用途、结构类型、修建时间3个指标来估计每间房屋的价值，具体的价值标准见表10。

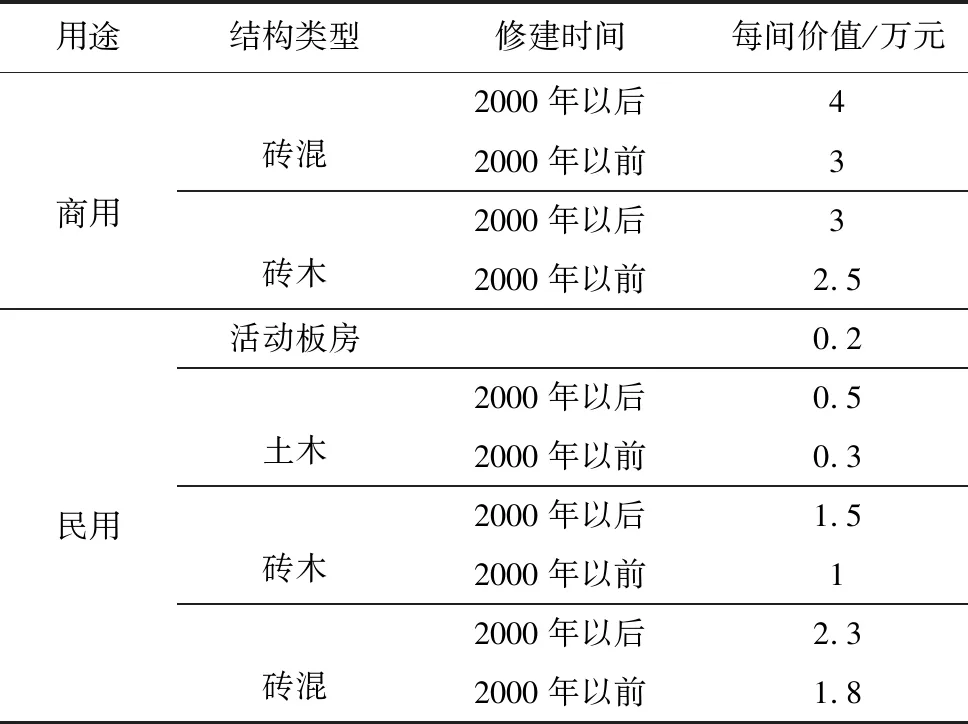
表 10 房屋价值评估表Table 10 Building valuation

最终得到的房屋财产分布如图 8所示。

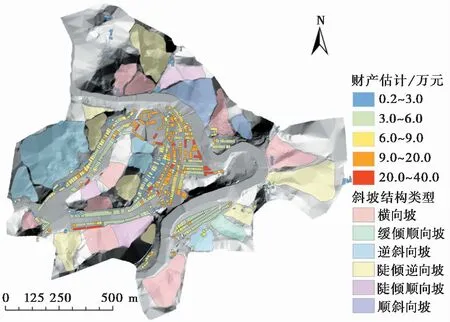
图 8 房屋财产价值分布图Fig. 8 Building value distribution

3.6 财产损失风险

综合风险评价4部分计算结果，通过财产风险评价计算公式(3)，评价结果可以以房屋或斜坡为单位进行表达(图 9)。

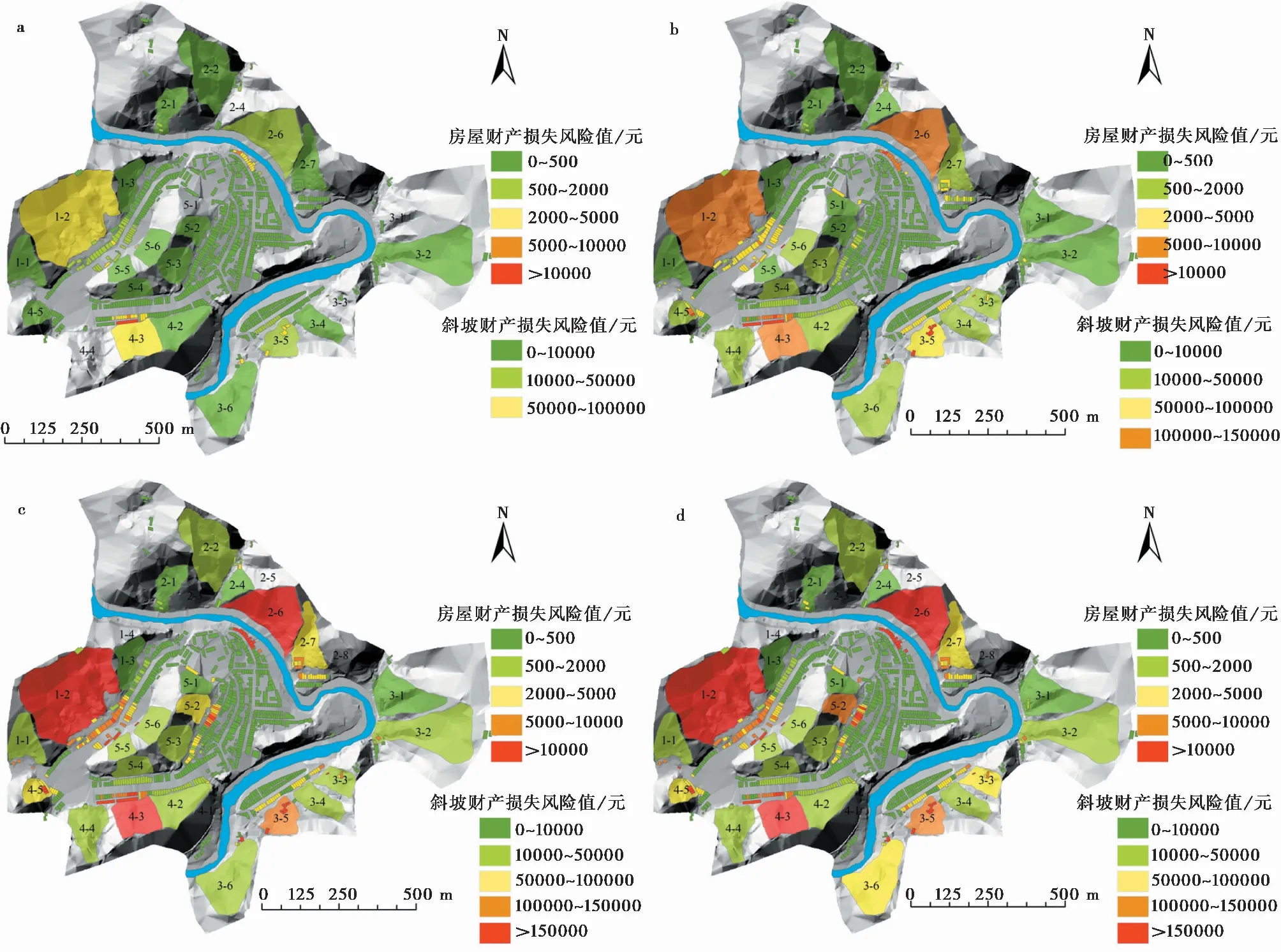
图 9 房屋/斜坡不同降雨条件下(连续五日)财产损失风险值分布图Fig. 9 Distribution of property loss risk under different rainfall conditions(5 consecutive days) for housing/slopea. 天然状态； b. 10年一遇； c. 20年一遇； d. 50年一遇

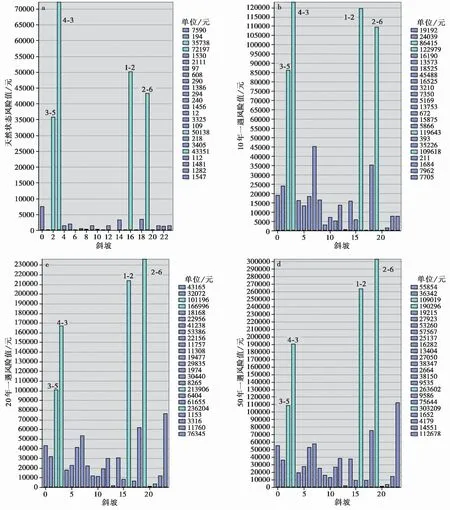
图 10 各斜坡在不同降雨条件下(连续五日)财产损失风险值分布图Fig. 10 Property loss risk distribution of each slope under different rainfall conditions(5 consecutive days)a. 天然状态； b. 10年一遇； c. 20年一遇； d. 50年一遇

天然状态下：房屋财产损失风险最大值为25i670元/年，年财产损失超过5000元的房屋共3栋，分布在4-3号斜坡下部，在实地调查中可以看到， 4-3号斜坡由于切坡修建房屋，斜坡危险性很高，导致4-3号斜坡影响范围内房屋的风险值均较高，而其他斜坡在天然状态下风险值均很低。

10年一遇降雨：房屋财产损失风险最大值为43i726元/年，年财产损失超过5000元的房屋共42栋，有9栋分布在3-5、4-5号斜坡上，由于斜坡上的房屋受斜坡的影响最为直接，易损性很高，导致3-5、4-5号斜坡坡上的房屋风险值均较高，其余位于4-3及2-6号斜坡的影响范围内，实地调查发现， 2-6号斜坡规模较大，为一凹形坡，碎石土在斜坡中下部集中，在接受强降雨的情况下，斜坡的作用强度高，导致房屋的风险值较高。

20年一遇降雨：该降雨条件下，单个房屋财产损失风险最大值为67i660元/年，年财产损失超过5000元的房屋共77栋，除分布在3-5、4-3、4-5斜坡影响范围内的，其余分布在斜坡2-6、2-7以及1-2影响范围内，与斜坡2-6相似，斜坡1-2也是一规模较大的凹形坡，但碎石土主要在斜坡下部集中，一般诱发滑动难度较大，滑动速度小。

50年一遇降雨：该降雨条件下，单个房屋财产损失风险最大值为77i878元/年，年财产损失超过5000元的房屋共84栋，除分布在1-2、2-6、2-7、3-5、4-3、4-5号斜坡影响范围内，由于降雨强度较大，斜坡的破坏概率整体会增高，其余斜坡范围内也有零星分布。

4 结 论

(1)考虑到区内降雨为诱发滑坡的第一要素，收集了研究区近年来的日值降雨数据集，采用P-Ⅲ型曲线进行拟合，得到兴隆镇10年一遇、20年一遇以及50年一遇持续五日的降雨强度分别为65.57imm·d-1、72.88imm·d-1、85.91imm·d-1。

(2)在实地调查的基础上，选取兴隆镇周边29个有隐患的斜坡，对其进行不同降雨工况下的破坏概率计算，用以表达斜坡的危险性，切合实际情况。

(3)在天然状态下，兴隆镇房屋年财产损失风险约22.8万元，造成财产损失较大(超过5万元)斜坡为1-2及4-3号坡； 10年一遇降雨条件下，房屋年财产损失风险约69.73万元， 1-2、2-6、4-3、3-5号坡造成损失较大； 20年一遇降雨条件下，房屋年损财产损失风险为122.5万元， 1-2、2-6、2-7、3-5、4-3、4-5及5-2斜坡造成损失较大； 50年一遇降雨条件下，房屋年财产损失风险为150.5万元，新增危险斜坡为3-3、及3-6号坡。

(4)在各类降雨条件中，斜坡1-2、2-6、3-5、4-3造成的财产损失总和与城镇财产损失总和的比例均超过55%，并且随着降雨强度的增加，其财产损失占比呈递减状态，在天然状态时，占比为88.33%，10年一遇降雨时，占比为62.90%，在20年一遇降雨时，占比为58.64%，在50年一遇降雨时，损失占比为57.54%，这说明随着降雨强度的增加，其他原本较为稳定的斜坡的危害潜力正逐步被“挖掘”，如图 10所示，同时也指出，对这4个斜坡进行重点的防治即可大量地削减城镇的财产损失风险。