凸优化问题的惯性Uzawa 方法
2020-05-25胡立亮方长杰
胡立亮, 方长杰
(重庆邮电大学 理学院,重庆400065)
本文考虑具有线性等式或不等式约束的强凸极小化模型,即求解下列问题:

其中,f:Rn→R 是σ -强凸但不必要光滑函数,强凸系数σ >0 未知,

是闭凸集.在问题(1)中的目标函数f(x)被视为给定的黑匣子[1],因此强凸系数σ 是不可计算的.假定问题(1)的目标函数是强凸的,因为这些模型在求解一些稀疏或低秩优化模型等领域中有着广泛的应用,参见文献[2 -3].对于原始问题(1),其Lagrange函数为

其中λ∈Rm是Lagrange乘子.令
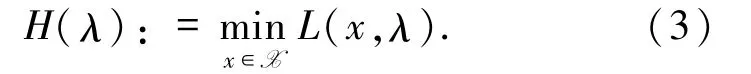
那么,问题(1)的对偶问题为

其中,如果Ax =b,则Λ =Rm.如果Ax≤b,则Λ =.设点(x*,λ*)∈X × Λ 是Lagrange 函数L(x,λ)的鞍点.因此,点(x*,λ*)∈X×Λ满足

称点(x*,λ*)是L(x,λ)的鞍点,即

Uzawa方法是求解L(x,λ)的鞍点问题的最基本方法[4].利用Uzawa 方法求解问题(1),可以得到下面迭代算法:

其中,τ >0 表示迭代步长,‖·‖表示一般的2 -范数.由于Uzawa方法在不同的领域中所起的重要作用,对Uzawa方法的研究吸引了许多学者的广泛关注[5-6].惯性型方法起源于含摩擦重球系统(HBF)的隐式离散化方法,其主要特点是每个新的迭代点依赖于前两次迭代[7].随后,将该惯性技术推广到求解极大单调算子的包含问题[8].近年来,惯性类型算法的研究越来越受到人们的关注;例如,惯性向前-向后分裂算法[9],惯性Douglas -Rachford分裂算法[10],惯性乘子交替方向法(inertial ADMM)[11],变分不等式的惯性型方法[12]等.关于凸优化问题在图像去噪中的应用,可以参考文献[6,13 -16]及其参考文献.
受上述研究工作的启发,提出了求解凸优化问题(1)的如下惯性Uzawa方法:


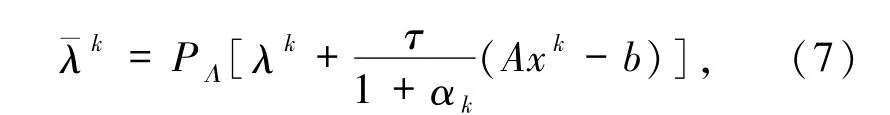
其中,PΛ(·)表示在集合Λ上的投影.
1 预备知识
下面介绍两个引理.
引理1.1[17]设f(x)为σ-强凸函数(其中σ未知),H(λ)为(3)式所定义,则有:
(i)H(λ)是连续可微的凹函数;
(ii)
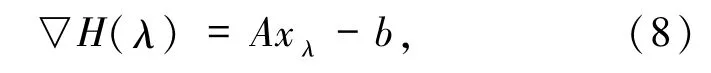
其中

引理1.2[14]设C 是Rn中的一个非空闭凸子集,则

2 主要结果
在这一节中,首先给出求解问题(1)的如下惯性Uzawa算法:
算法2.1
步骤0:任取λ0∈Λ,τ0>0,αk≥0(k =1,2,...)及x0∈Rn.
步骤k:更新(λk,xk,τk)使其满足

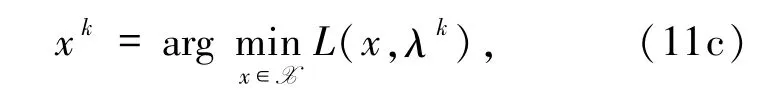
和

注2.1 根据(8)式,很容易看出(11a)式可以改写为

在(12)式中,根据引理1.1(iii),只要

就得到(12)式满足.于是,至少当

不等式(12)是满足的,即{τk}存在上界.在算法2.1中,任意给定正数τ0,在每次外循环中内嵌一个内循环用于更新τk,通过有限次减小τk,必定能够使得τ(i)k满足(12)式,并令τk=τ(i)k,i =1,2,….因此,根据算法2.1 得到的序列{τk}是有界的,即对任意整数k,
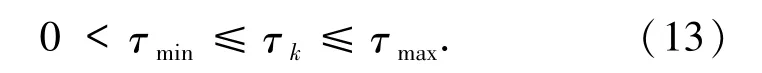
注2.2 现在,比较下算法2.1 与文献[15]中的算法1.首先,算法中初始迭代点x0∈Rn是任意选取的,而文献[15]中,选择初始点x0为目标函数为L(·,λ)极小化模型的最优解;其次,与文献[15]的算法1 相比,增加了惯性项,参见(6b);此外,非负数αk(k =1,2,…)可以任意选择;参见算法2.1 中的(11b).此外,得到了与文献[15]的方法相同的收敛速度;同时,通过数值实验,验证了所提出方法的有效性.

引理2.1 假设{(xk,λk)}是由算法2.1 产生的序列对,则

其中xλ由(9)式所定义,λ∈Λ.
证明 根据(11c)有,存在yk-1∈∂f(xk-1)使得

因此
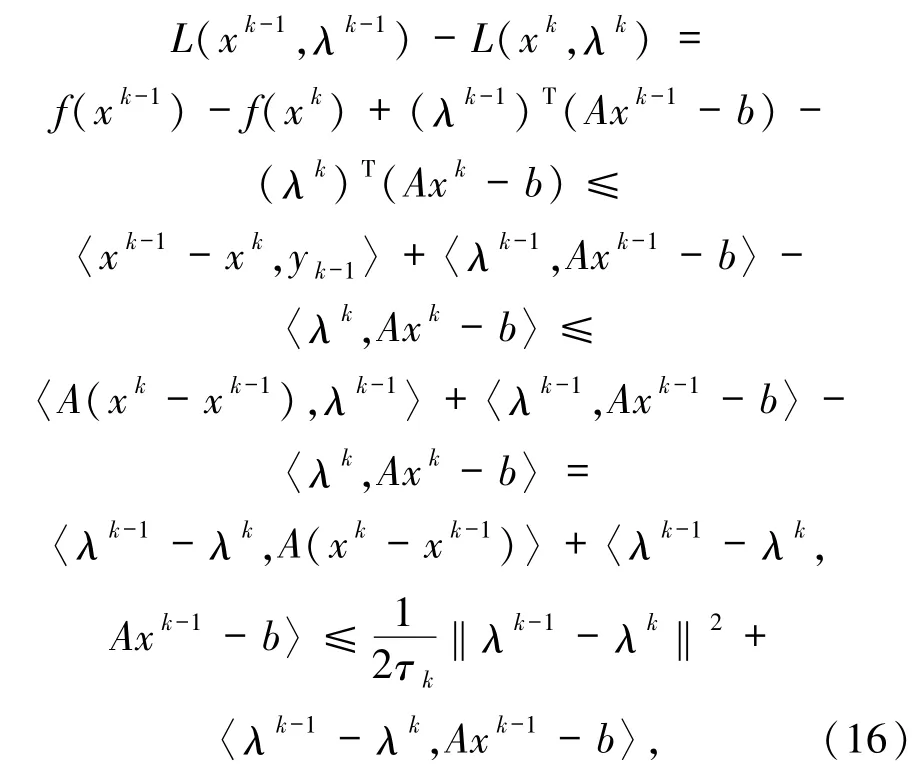
其中第一个不等式根据f(x)的凸性,第二个不等式根据(15)式,而最后一个不等式是根据(12)式.
类似地,根据(9)式有

其中yλ∈∂f(xλ).因此

结合(16)和(17)式有

根据(11a)式有

根据(11b),又可以得到

和

在(19)式中令λ =λk-1有

因此,根据(20)~(22)式有
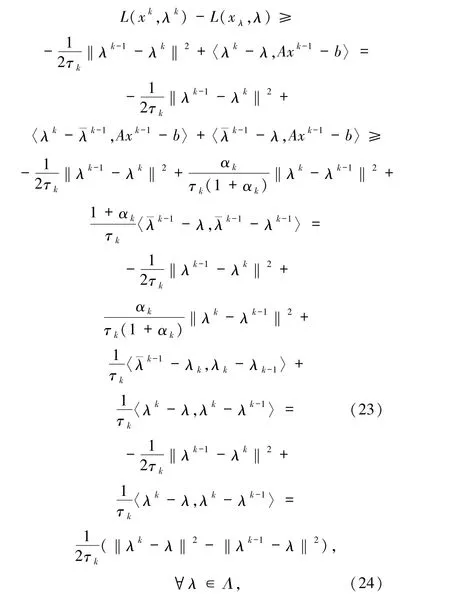
从而(14)式成立.
注2.3 如果在(23)式中取λ =λk-1,则有

这说明算法2.1 产生的序列{L(xk,λk)}是单调非减的.
定理2.1 假设序列对(xk,λk)由算法2.1 所产生,则
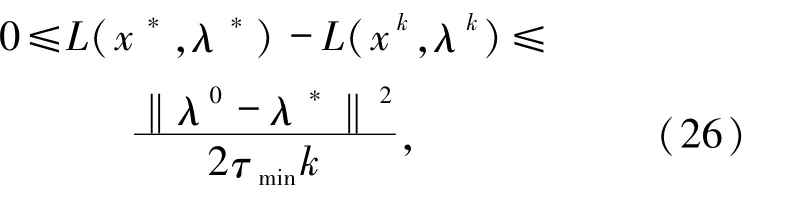
其中(x*,λ*)是L(x,λ)的一个鞍点.
证明 根据鞍点的定义,左边第一个不等式显然成立.现在证明第二个不等式.在(25)中取k =n,根据{τk}的有界性(参见(13)式)有


那么,序列{L(xn,λn)-L(x*,λ*)}单调递增.在(14)式中,令xλ=x*,λ =λ*,k =n有
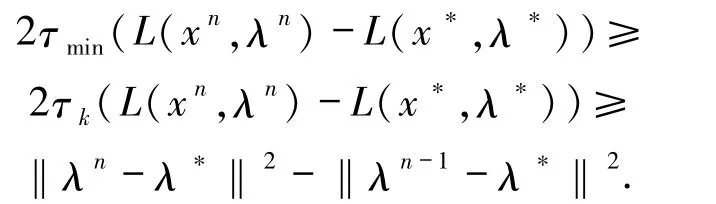
因此,

根据{L(xn,λn)-L(x*,λ*)}的单调性和(27)式有
从而(26)式成立.
3 数值实验
在这一节中,将提供一些数值实验来验证算法的有效性.这些数值都是用Matlab 在CPU 型号为Inter(R)I5 -5200U 的笔记本电脑上运行的结果,Matlab版本为5.5.0.197613(R2015A)SP1.It表示迭代次数,CPU表示运行时间,Tol表示迭代停止条件,由(30)式所定义,PSNR 表示峰值信噪比,该指标用于衡量图像恢复的质量,由(31)式所定义,Rel表示相对误差,用以衡量图像恢复质量的准确度,由(32)式定义.考虑一个具有盒约束的图像去模糊模型并应用算法2.1 求解下列约束线性最小二乘问题[15]

其中,K,D∈Rn×n,c,l,u∈Rn,μ >0.该模型是求解具有盒约束的图像去模糊问题,其中x 是待恢复的数字图像的向量表示,K是模糊算子(积分算子),c是模糊图像的矢量表示,l、u 分别是像素值的上下界.假设N(K)∩N(D)={0},其中N(·)表示零空间,重写问题(28)得到
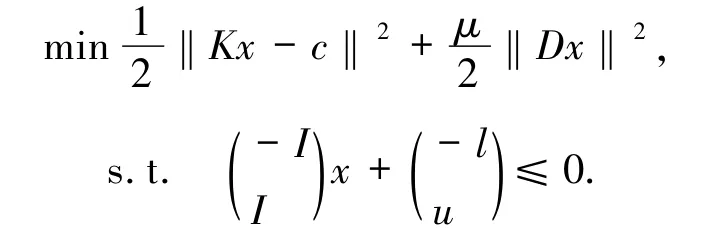

且CTol≤10-2.
测试了2 张图片,如图1 所示,图1(a):128 ×128,图1(b):256 ×256.观测图像c 可表示为c =K¯x+ρr,其中¯x表示原始图片,r 表示服从标准正态分布的随机向量,ρ 表示高斯噪声的级别.使用MATLAB代码:K =fspecial(‘average',Ksize)和C =imfilter(X,K,‘circular',‘conv')+ρ*randn{m,n}由不同大小的模糊核产生的模糊图像,其中Ksize表示模糊核的尺寸,X表示原始图片,C表示观察图像.

图1 原始图片Fig. 1 Original picture
用峰值信噪比PSNR(dB)来度量去噪后图片的质量,其定义如下:

其中

进一步,相对误差的“Rel”定义如下:

3.1 所提出算法有效性的数值结果 在表1、表2中,UA和InUA 分别表示文献[15]中的算法1 和本文算法2.1,Tot表示步长τk调整的次数.表1 为图1(a)图像的测试结果,其参数选择如下:τ0=1.0,λ0=0,αk=1.8,η =3,测试Ksize分别为11、17、23 和25 的不同情形下的模糊图像.表2 为图1(b)图像的测试结果,参数设定为:τ0=0. 9,λ0=0,αk=1.0,η =3,测试Ksize分别为15、19、21和25 的不同情形下的模糊图像.

表1 测试图1(a)的数值实验结果Tab. 1 The numerical results of testing figure 1(a)

表2 测试图1(b)的数值实验结果Tab. 2 The numerical results of testing figure 1(b)
3.2 图像去噪 本节将考察本文的方法在图像去噪中的应用.结果主要基于表1 和表2 中的数据.这些数据结果表明,提出的算法能够得到比文献[15]中的算法1 更好的恢复图像的质量(即更高的PSNR值).
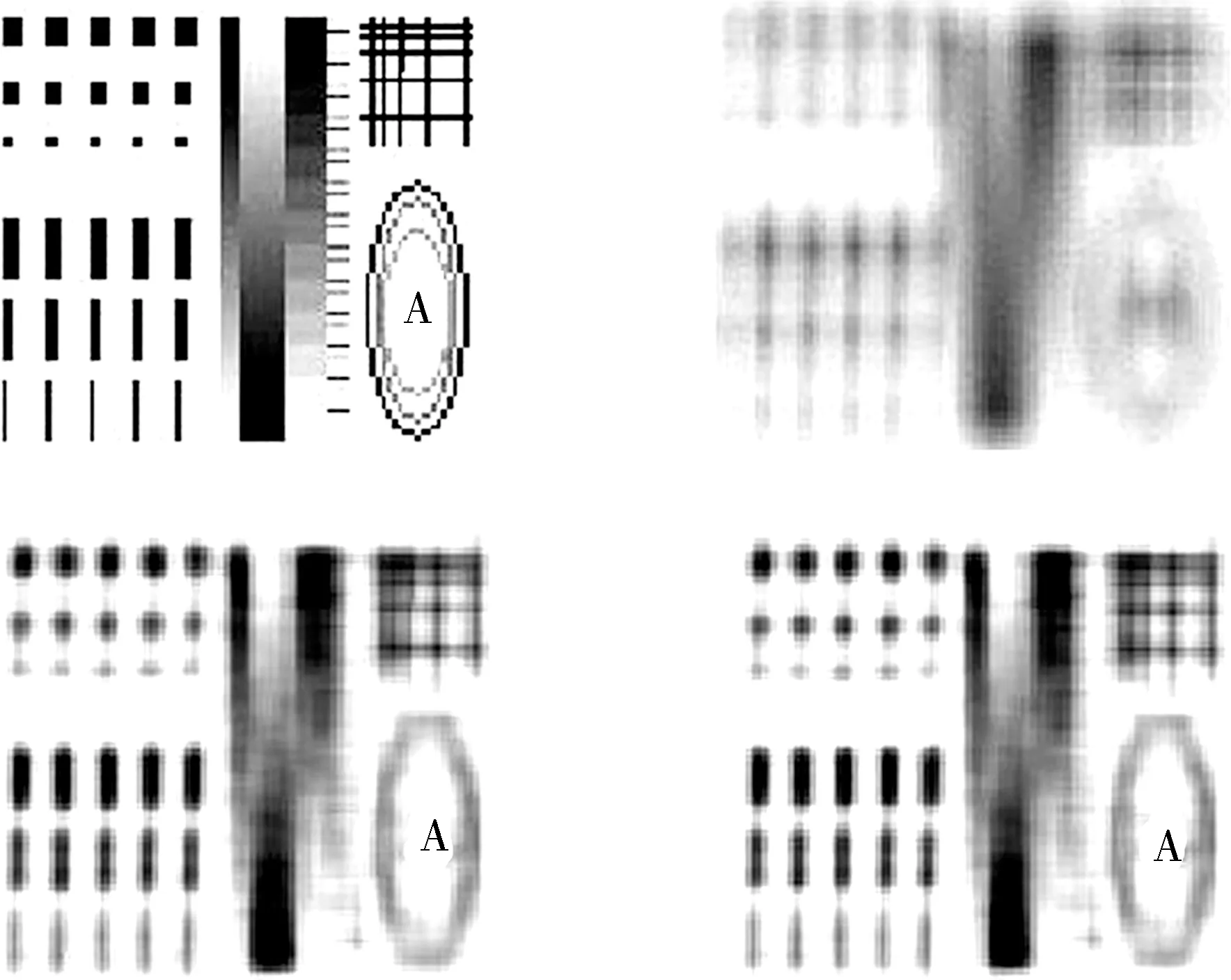
图2 图1(a)的原始图片、噪声图片、UA算法恢复图像和InUA算法恢复的图像,模糊核尺寸为11Fig. 2 Original image,noise image,UA algorithm restored image and InUA algorithm restored image of Fig. 1(a),the size of blurred core is 11

图3 图1(b)的原始图片、噪声图片、UA算法恢复图像和InUA算法恢复的图像,模糊核尺寸为15Fig. 3 Original image,noise image,UA algorithm restored image and InUA algorithm restored image of Fig. 1(b),the size of blurred core is 15
3.3 与其他现有方法的比较 本节将算法2.1 与文献[16]中的PDHG方法和文献[6]中的CP方法进行比较.表3 给出了在前20 次迭代内3 个算法所用的时间和PSNR 值.另外,给出了当Ksize =21时,3 个算法的PSNR值得变化趋势图(图4).从图4 可以看出,在运行时间比较接近的情况下,算法2.1(InUA)的PSNR 值更高;同时,从图4 可以看出,的算法相对稳定,而PDHG 方法在处理模糊程度较高的模糊图像(如ρ =3)时,其PSNR值有向下趋势的,即处理能力逐渐下降.
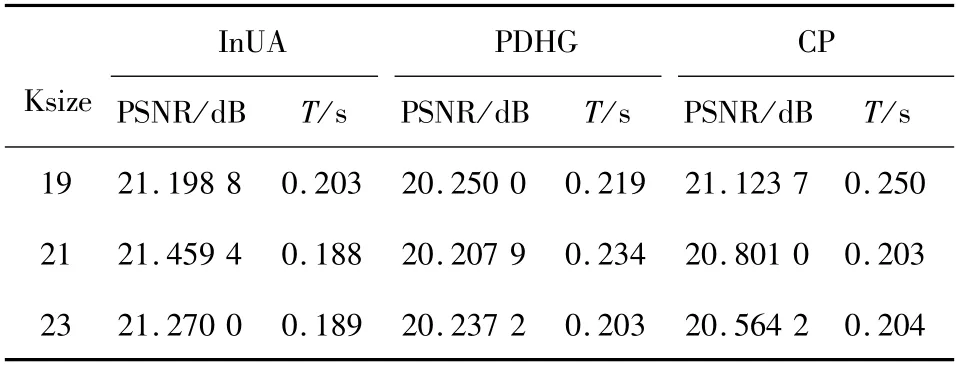
表3 不同尺寸下PSNR值和运行时间的比较Tab. 3 Comparison of PSNR value and running time under different sizes


图4 20 次迭代,PSNR值曲线图Fig. 4 PSNR value curve by 20 iterations
