闭链式四足机器人对角小跑步态规划与仿真分析*
2020-05-25汪永明马腾飞
汪永明,马腾飞,韦 强
(安徽工业大学 机械工程学院,安徽 马鞍山 243032)
0 引 言
相对于轮式机器人,步行机器人[1-3]的地面适应性强,越来越引起国内外学者的广泛关注。为了实现步行腿机器人在复杂地形下的稳定快速行走,首先需要解决其步态的合理规划问题。
山东大学的孟健等[4]为实现四足机器人在平面和斜坡上的全方位移动,提出了基于对角小跑步态的运动控制方法;国防科学技术大学的谢惠祥等[5]为了解决四足机器人对角小跑运动中机体绕对角线翻转的问题,提出了一种利用支撑腿的髋部侧摆关节力矩来平衡机体翻转的姿态控制方法,并分析讨论了姿态控制可能引起的机体侧向运动现象;北京理工大学的郝仁剑等[6]为保证大负重四足机器人的全方位稳定行走,提出了基于速度矢量的间歇步态规划方法,采用间歇步态作为主步态,将平动与转动速度矢量映射为绕旋转中心转动;上海交通大学的何冬青等[7]对四足机器人对角小跑步态下绕支撑对角线的翻转力矩建立了力学模型,提出了三分法来分析该力矩对机器人运动姿态及稳定步行的不利影响;上海理工大学的勾文浩等[8]针对一种电驱动四足仿真机器人,提出了一种对角小跑步态规划方法实现机器人的连续平稳行走;太原理工大学的原刚等[9]针对实际行走轨迹与规划轨迹存在较大偏差的问题,提出了一种混合算法使其直线轨迹偏差减小;FRANCO G等[10]为了防止仿人机器人NAO在滑面上行走时摔倒,提出了一种基于步长、步行速度等参数变化的仿人步态控制策略,利用机器学习技术来调整步态参数和关节修正,以达到期望的零力矩点ZMP(Zero Moment Point)轨迹,使机器人更能抵抗打滑和外部干扰;TEDRAKE R等[11]提出了一种关于零力矩点(ZMP)跟踪的连续时变线性二次型调节器问题的闭式解决方案,通过允许对期望的ZMP进行“软”跟踪(以二次型代价),通过在线重新计算最佳控制器实现了Atlas仿人机器人的动态步行;BALAKRISHNAN S等[12]为规划和控制两足机器人在不平坦地形上的稳定行走,把机器人建模为非线性3D倒立摆,并推导出了ZMP与机器人质心之间的关系,并通过模拟和实验验证了机器人在连续不平坦的地形上平稳行走。
本研究针对步行机器人的快速稳定行走需求,以一种双闭链式四足机器人为研究对象,对其进行对角小跑步态规划。
1 闭链式四足机器人机构原理
闭链式四足机器人的机构原理如图1所示。
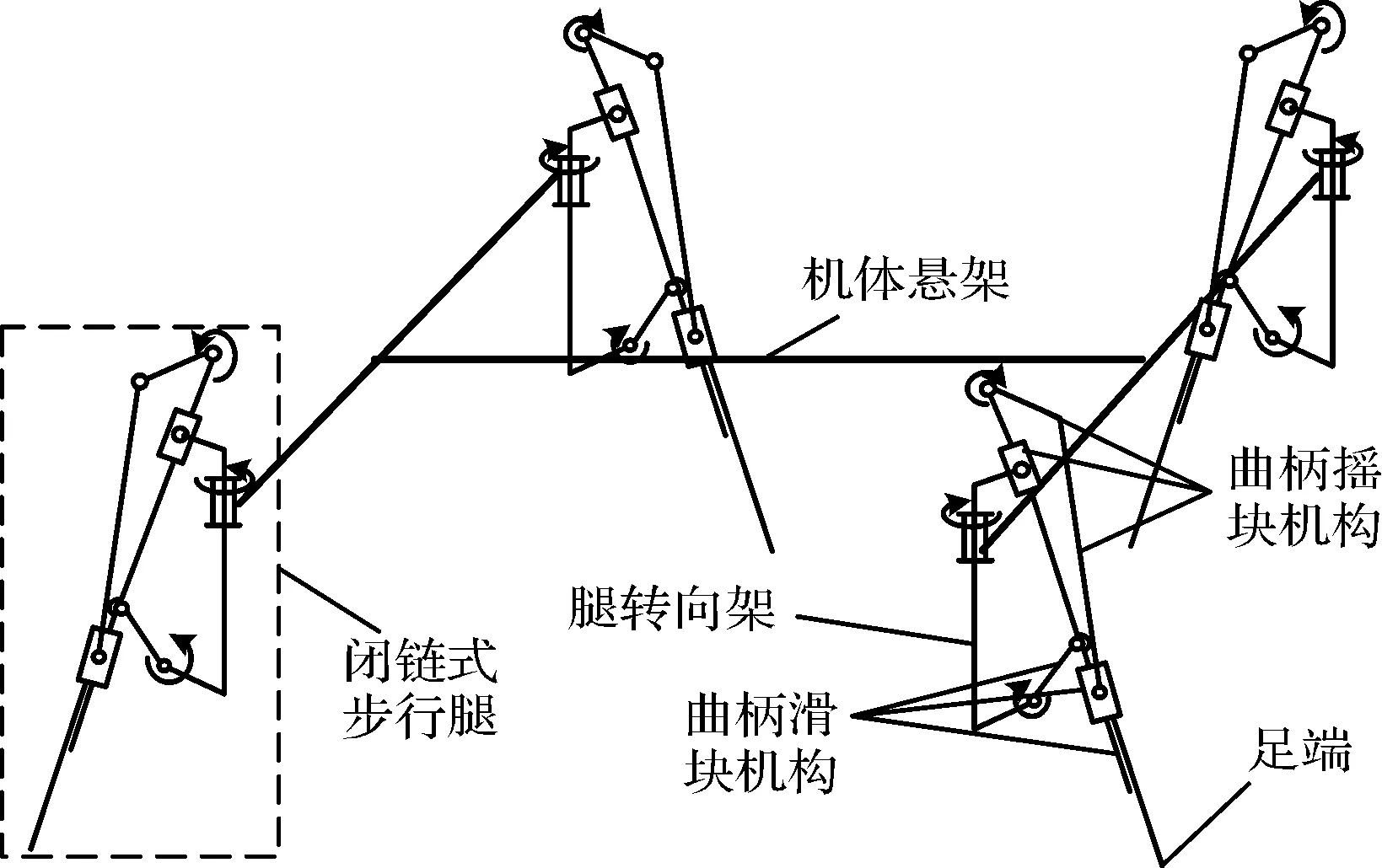
图1 闭链式四足机器人机构原理
由图1可知,该四足机器人主要包括机体悬架、腿转向架和4条闭链式步行腿。其中,闭链式步行腿具有两个闭链,其主闭链采用曲柄摇块机构,用于实现步行腿的跨步摆腿动作,其副闭链采用曲柄滑块机构,用于调节足端运动轨迹。当主闭链的曲柄转动时,会带动连杆上下移动和产生一定程度的摆动。如果将连杆反向延长,其末端的轨迹接近于机器人腿机构的足端轨迹。另外,其副闭链的曲柄一端固定在曲柄摇块机构的连杆之上,当曲柄转动时,带动滑块结构的腿部沿着连杆移动,从而调节腿部的长度,在机器人移动过程中可通过对腿部长度的调节达到不同的步行运动效果。
2 四足机器人对角小跑步态规划
机器人运动主要是靠腿部机构按照设定好的运动方式完成周期运动来实现的。四足动物的典型步行步态有:行走步态、对角小跑步态、溜蹄步态、跳跃步态和奔跑步态。其中,对角小跑步态是四足动物最常见的中高速行走步态。本文针对闭链式四足机器人,开展对角小跑步态规划研究,以期为机器人的稳定性控制提供理论基础。
在对角小跑步态下,四足机器人只有两条腿支撑,另两条腿处于腾空摆动状态。若不考虑机器人足端结构,其着地端仅仅为两着地足构成的支撑线,不能构成稳定多边形区域。
四足机器人的动态稳定支撑面示意图如图2所示。
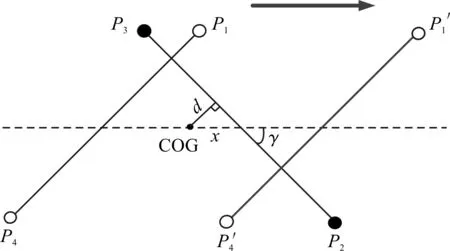
图2 四足机器人的动态稳定支撑面示意图
图2中显示四足机器人的腿2和腿3落地支撑(支撑线为P2P3),腿1和腿4腾空摆动时的状态。随着机器人的运动,其机体重心(center of gravity,COG)无法始终保持在支撑线上。当机器人以动平衡状态进行步行运动时,机体重心COG的位置和加速度发生实时变化,由此产生的前向和侧向的惯性如果不能被控制,会使机器人的运动发生失稳,机体可能会发生倾覆。
理论上,四足机器人在步行过程中需要保持零力矩点ZMP始终在着地足形成的支撑线上,这样机体才能在运动过程中保持稳定。在实际过程中,由于四足机器人的运动会造成机体绕支撑对角线产生倾翻力矩,这个力矩会造成四足机器人在运动过程中机体姿态的变化。如果机体的倾翻角θ过大,对角线上的前后两摆动腿无法同时着地,会造成四足机器人无法完全按照规划的步态运动。在运动过程中,倾翻角θ的增大会影响四足机器人的稳定性,累积到一定程度会使四足机器人发生倾倒。
为了分析倾翻角θ对四足机器人运动影响,要对倾翻力矩建立力学模型。在理想状态下,四足机器人以对角小跑步态匀速前进,四足机器人的质量对称均匀分布,假设质量集中在四足机器人机体的几何中心COG(如图2所示),根据刚体绕定轴转动的微分方程,可得:
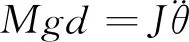
(1)
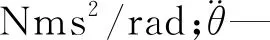
图2中,x是四足机器人机体重心COG点沿着前进方向到支撑线的距离,是随四足机器人运动实时变化的。在四足机器人完成一个运动周期过程中,x可表示为:
x=kλ-vt
(2)
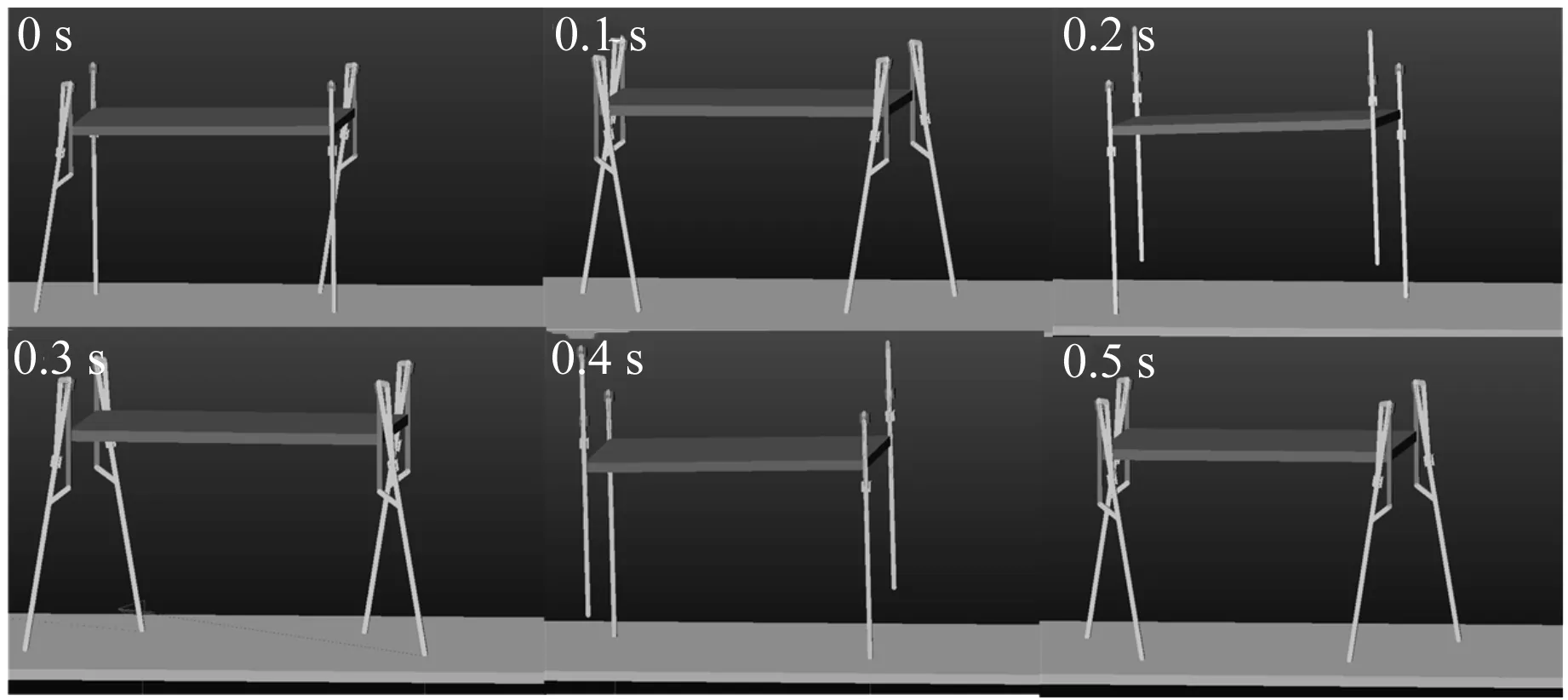
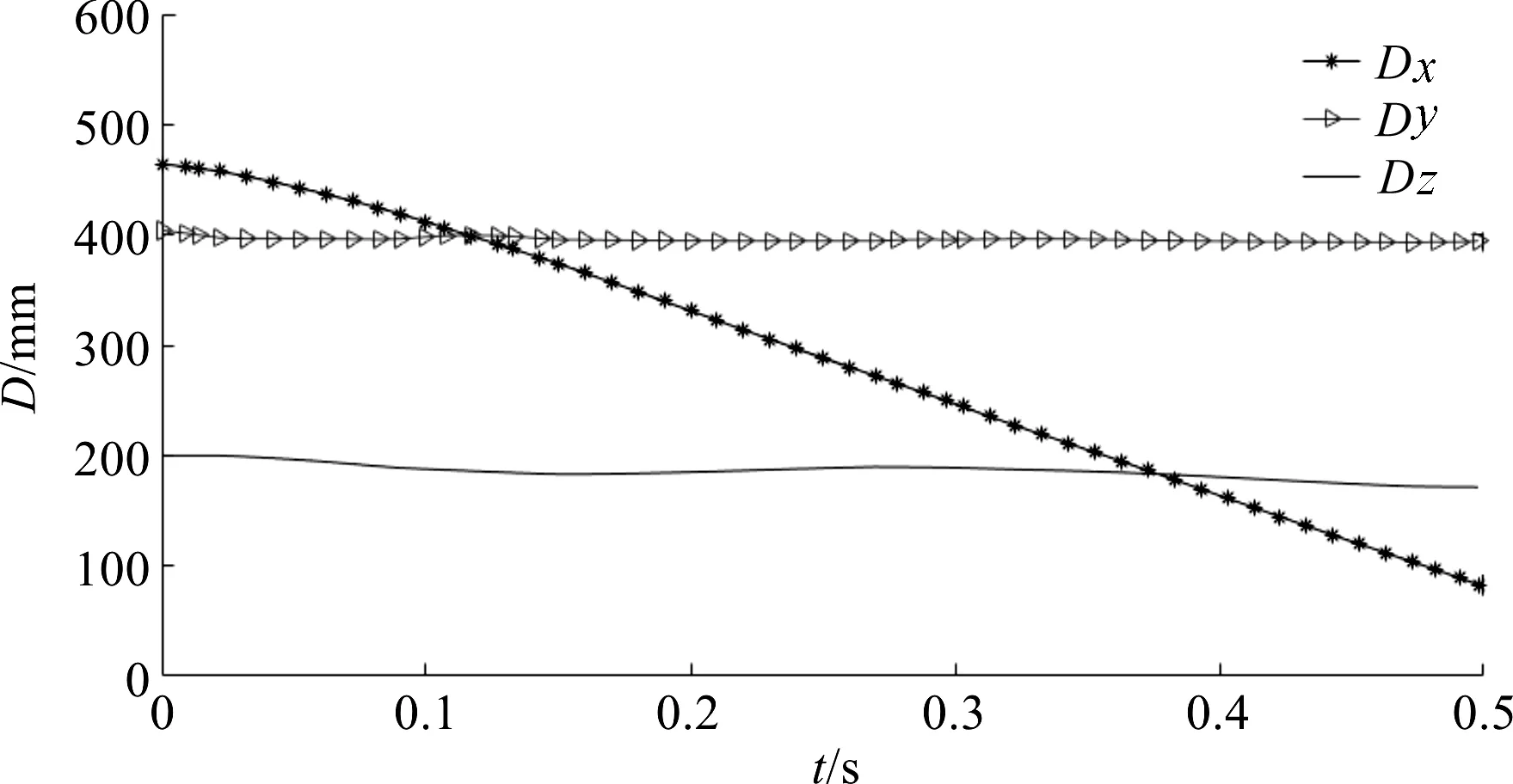
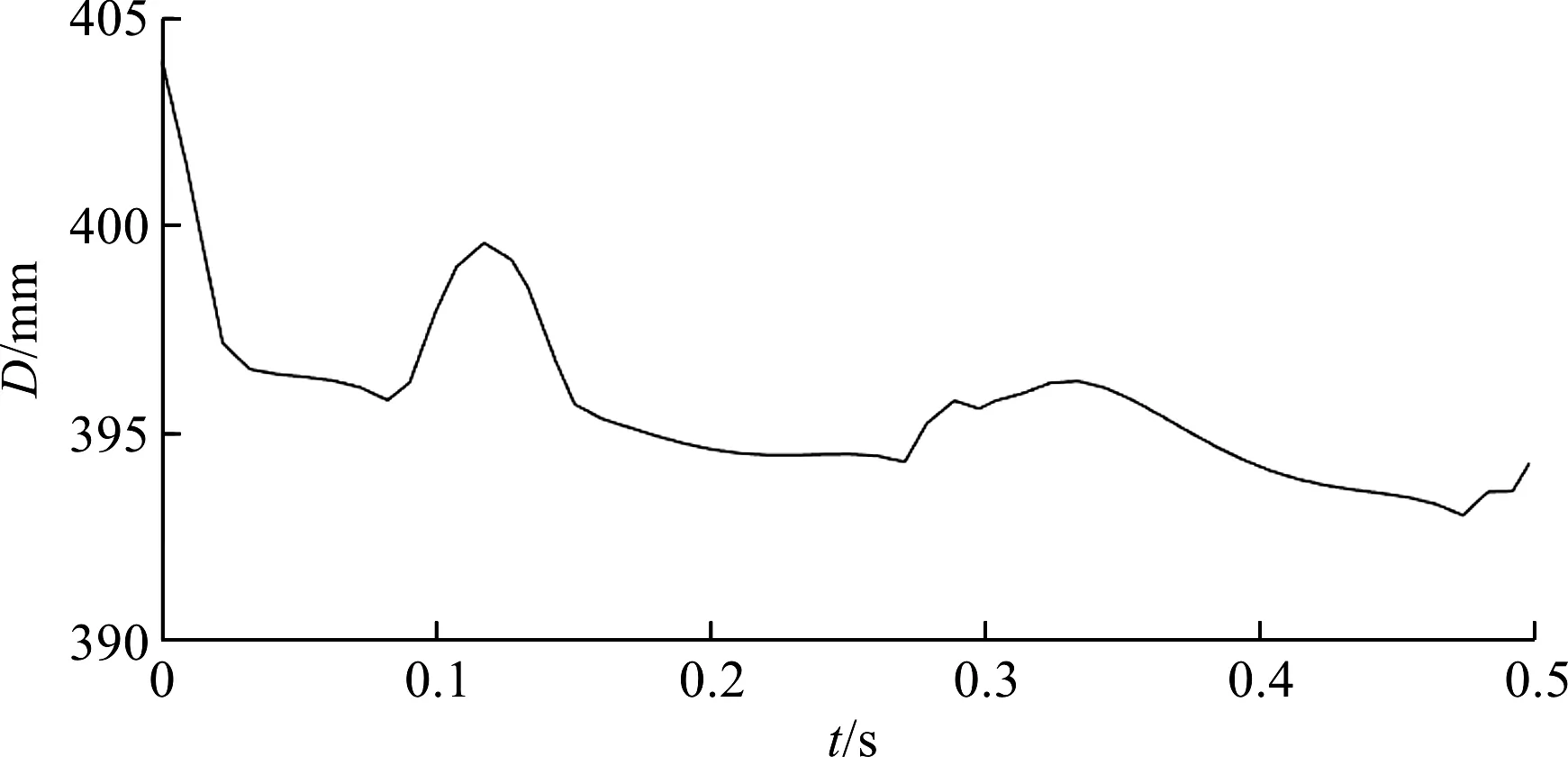
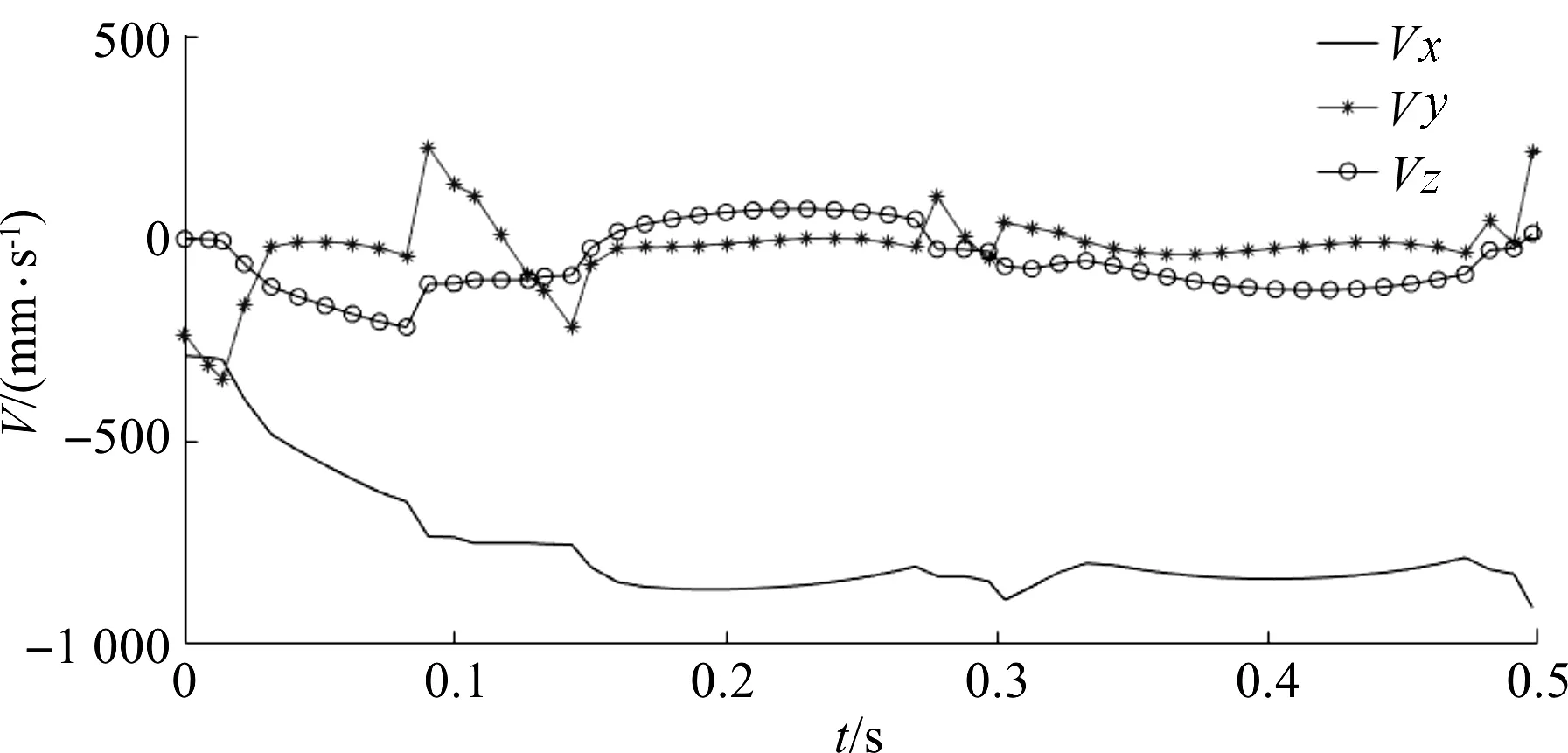
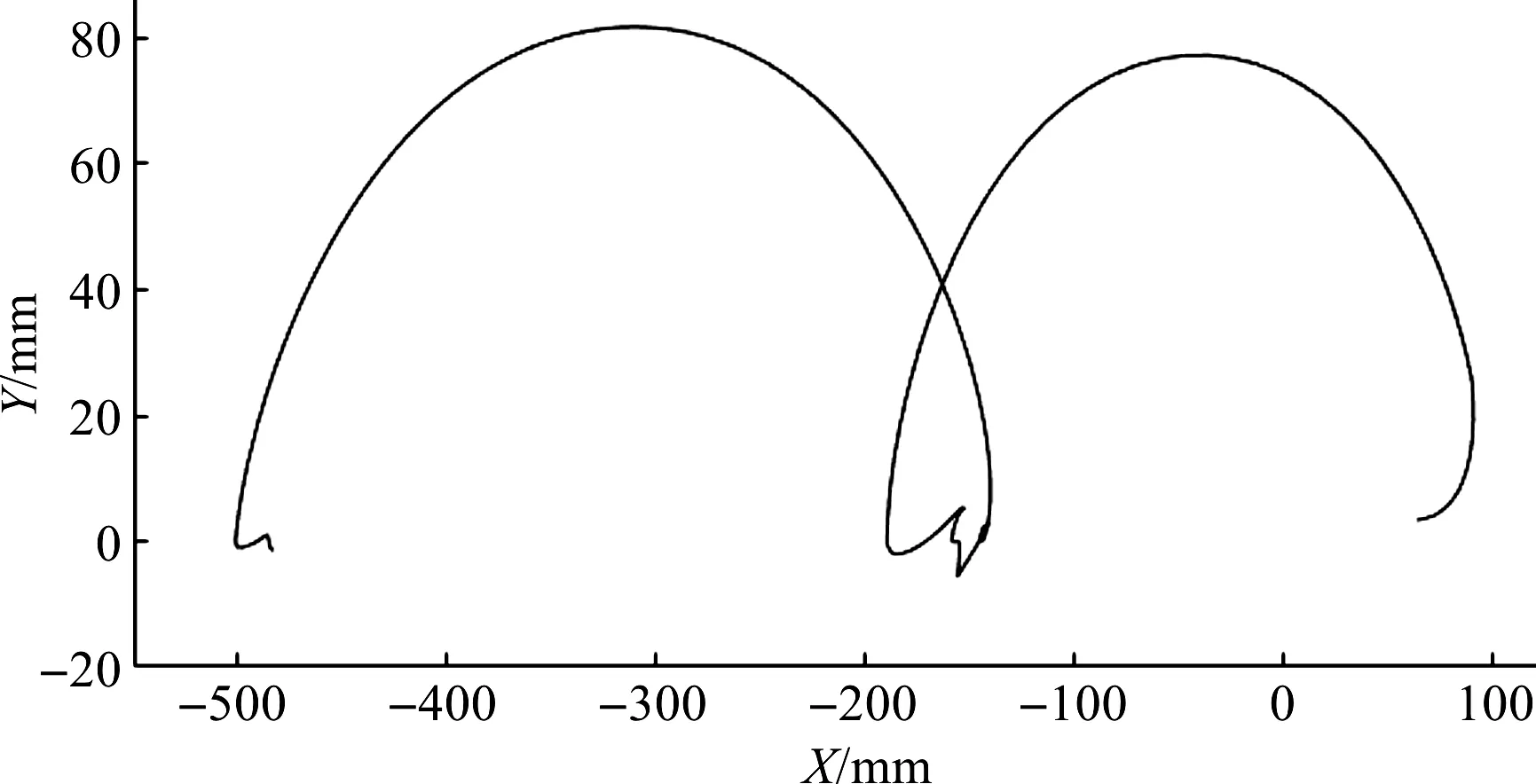
式中:λ—步距,m;k—起步参数,0 由图2中的x和d的三角函数关系可得: d=xsinγ (3) 式中:γ—四足机器人前进方向与支撑线的夹角。 将式(2,3)代入式(1)中,并对式(1)自变量时间t积分,可得到倾翻角速度,再次积分可得到倾翻角,即: (4) (5) 式中:A=Mgsinγ/J。 当四足机器人的机体产生倾翻运动时,其时间t可以通过占空比β和运动周期T来计算,即:t=(1-β)T,代入式(5)可计算出倾翻角θ: (6) 由式(6)可以看出,四足机器人运动过程中的倾翻角θ与k、T、β和λ有关;只有当倾翻角θ为0时,四足机器人的两条对角摆动腿才能同时落地。同时,为了保证机器人动态行走过程的稳定性,其倾翻角速度越小越好。 取对角小跑步态的占空比β=0.5。在这种情况下,四足机器人以对角的两条腿为一组,分别处于支撑相和摆动相,如当腿1和腿4开始抬起进行摆动时,腿2和腿3着地起支撑作用。 将β=0.5代入式(6),可以得到四足机器人运动过程中的倾翻角θ,即: (7) 当6k-1=0(即k=1/6)时,四足机器人在支撑相中的倾翻角θ为0,理论上,此时四足机器人两条摆动腿能够同时着地。 根据占空比β=0.5将对角小跑步态的运动周期T分为2个子周期,分别对应一组对角腿的支撑相和摆动相。 对角小跑步态是对称步态,所以各腿的摆动顺序并没有受到实际影响,四足机器人对角小跑步态的迈腿时序图如图3所示。 图3 四足机器人对角小跑步态的迈腿时序图 为了减小ADAMS建模和仿真的工作量,并且尽量体现闭链式四足机器人的运动性能,根据其机构原理,笔者对关节零件作简化处理,建立闭链式四足机器人虚拟样机模型。 其中,闭链式四足机器人虚拟样机参数如表1所示。 表1 闭链式四足机器人虚拟样机参数 根据足端轨迹设计,该四足机器人的腿部为摆动相时,其主闭链曲柄旋转角度为:-36°≤α≤216°;该四足机器人的腿部为支撑相时,其主闭链曲柄旋转角度为:216°≤α≤324°,所以其摆动相的转动角度为252°,支撑相的转动角度为108°。 笔者取主副闭链曲柄的转角速比为1∶2,根据上述对角小跑步态规划的运动规律,在ADAMS中进行驱动函数设计,四足机器人对角小跑步态下的腿部主副闭链驱动函数如表2所示。 表2 四足机器人对角小跑步态下的腿部主副闭链驱动函数 表2中,t1,t2,t3为3个不同的阶段:t1为姿态调整阶段(0~0.1 s);t2是前半周期(0.1 s~0.3 s),即2、3腿为摆动相,1、4腿为支撑相;t3是后半周期(0.3 s~0.5 s),即2、3腿为支撑相,1、4腿为摆动相。t2和t3组成一个完整的迈步周期。 在驱动函数中,“a”表示主闭链转动角度,“b”表示副闭链转动角度,下标中的第一位数字表示阶段,第二位数字表示机器腿的组别(“1”表示腿2和腿3,“2”表示腿1和腿4),驱动函数中的“kv”为速度调节系数,用来调节运动速度。 首先笔者根据表2中的驱动函数,在Matlab软件中规划出各个驱动的角度变化值,然后导入ADAMS中形成spline曲线,再利用其来驱动四足机器人按照对角小跑步态进行运动。 设仿真时间为0.5 s,包括0.1 s的姿态调整和周期为0.4 s的对角小跑步态运动,闭链式四足机器人对角步态仿真过程截图如图4所示。 图4 闭链式四足机器人对角步态仿真过程截图 图4中的截图分别为四足机器人在0 s、0.1 s、0.2 s、0.3 s、0.4 s和0.5 s这6个时间点的运动状态。在仿真过程中,0~0.1 s为机器人的姿态调整阶段,主要是保持机体质心有越过支撑点连线的趋势,为后面的对角小跑步态提供基础速度。 在0.1 s~0.3 s前半周期,腿2和腿3为摆动相,腿1和腿4为支撑相,机器人完成前0.5T的对角步态;在0.3 s~0.5 s后半周期,各腿状态正好与上一阶段相反,腿2和腿3为支撑相,腿1和腿4为摆动相。以此为周期,各对角腿组依次完成支撑和摆动,保持机器人前进运动。 四足机器人机体质心在xyz方向上的位移曲线如图5所示。 图5 四足机器人机体质心在xyz方向上的位移曲线 在图5中,x方向为机体的前进方向,y方向为竖直方向,z方向为左右方向。由图5曲线可知,闭链式四足机器人机体质心的位移在y方向和z方向变化量相对于x方向来说较小。由于0~0.1 s是机器人的姿态调整阶段,主要讨论0.1 s~0.5 s周期的对角小跑运动过程。根据ADAMS仿真数据可得,在0.1 s~0.5 s时间段,机器人机体在x方向移动的距离约为340 mm,由此可计算出对角小跑步态下,闭链式四足机器人在前进方向的移动速度约为0.85 m/s,能够达到中等速度的运动。 单独把竖直方向上的运动数据提取出来,四足机器人机体在y方向上的位移曲线如图6所示。 图6 四足机器人机体在y方向上的位移曲线 由图6可知,除了0~0.1 s的姿态调整阶段外,机器人在对角步态下行走过程中,其机体y方向位移波动很小,其最大值为397.1 mm,最小值为393.5 mm。所以四足机器人在对角步态下,其上下起伏度约为3.6 mm,能够保持稳定行走。 四足机器人机体质心在xyz方向上的速度曲线如图7所示。 图7 四足机器人机体质心在xyz方向上的速度曲线 除去0~0.1 s机器人起步时的姿态调整阶段,图7中xyz这3个方向的速度曲线均在0.3 s和0.5 s这两个时间点附近发生不规则的变化,这是由于闭链式四足机器人的摆动腿和支撑腿在这两个时间点相互切换,由足端落地时产生的振动所导致的,该现象可以通过改进控制方法和添加足端构件来进行改善。 以左后腿为例,笔者进行足端运动研究,四足机器人对角步态下的足端轨迹如图8所示。 图8 四足机器人对角步态下的足端轨迹 图8中,足端轨迹由两段组成,从右往左依次对应的是0~0.1 s的姿态调整阶段的足端轨迹和0.1 s~0.5 s的对角步态下的足端轨迹。可以看出,足端在两个阶段的连接处存在一定的不规则运动,这是由于闭链式四足机器人在运动过程中,其摆动腿和支撑腿的相互切换不稳定造成的。其对角步态下的足端轨迹步长约为350 mm,步高约为80 mm。 四足机器人对角步态下足端xyz方向速度曲线如图9所示。 图9 四足机器人对角步态下足端xyz方向速度曲线 由图9可知,在0.1 s~0.3 s时足端速度基本为0,此时足端处于支撑相;而在0~0.1s和0.3 s~0.5 s时,足端速度呈周期性变化,足端在0 ~0.1 s时为起步时的姿态调整阶段,而在0.3 s~0.5 s时是处于摆动相。 同时,在0.1 s、0.3 s和0.5 s这几个时刻,足端的运动速度都发生了不规则的变化,这与前面机体的运动分析是一致的,都是由足端落地时产生的振动导致的。 (1)针对双闭链式四足机器人快速行走需求,笔者运用零力矩点ZMP理论来讨论四足机器人的动态稳定性,推导出了机器人绕支撑对角线发生失稳时的倾翻角θ表达式,理论得出当6k-1=0时,双闭链式四足机器人在支撑相中的倾翻角θ为0,此时双闭链式四足机器人两条摆动腿能够同时着地; (2)建立了双闭链式四足机器人的模型样机,基于对角小跑步态来规划步行腿主副闭链的驱动函数,运用ADAMS对机器人进行运动仿真实验,获得其机体质心和足端运动轨迹。仿真结果表明:该双闭链式四足机器人,其对角小跑步态下的移动速度约为0.85 m/s,上下起伏度约为3.6 mm,能够达到中等速度下的稳定行走运动。其足端轨迹的步长约为350 mm,步高约为80 mm,基本满足跨步需求; (3)本研究提出的驱动控制方法,可以实现四足机器人对角小跑步态下的中速平稳行走。此外,该控制方法的姿态调整时间短,其腿部驱动函数简单、变量少,便于驱动控制,有利于后续实体样机的驱动实验。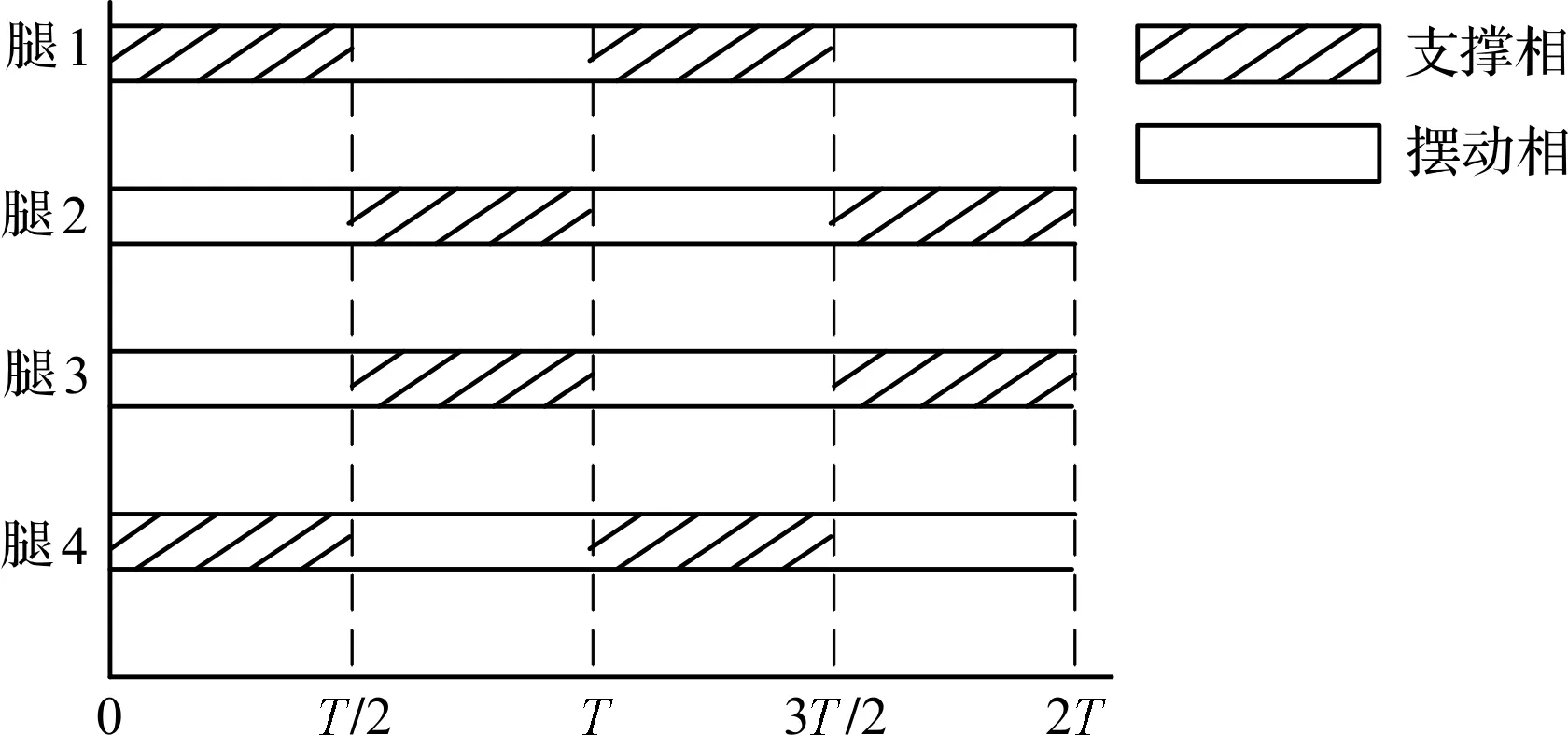
3 四足机器人运动仿真与分析
3.1 对角小跑步态仿真

3.2 仿真结果分析

4 结束语
