例析向量问题的精彩交汇

■冯克永

向量是高中数学的核心内容，又是高考的一大热点，是高中数学知识的一个重要交汇点，已成为联系其他数学知识的媒介。

一、与集合的交汇问题

例1 已知集合A={a|a=(x+y，3)}，B={b|b=(5，x-y)}，求A∩B。

解：由题意可得a=b，即解得

二、与函数的交汇问题

例2 已知向量若函数f(x)=a·b-2t|a+b|的最小值是求t的值。

解：由a·b=cos 2x，|a+b|=2 cosx，可得f(x)=2 cos2x-4tcosx-1。令s=则f(s)=2s2-4t s-1，s∈[0，1]。①当t≤0，s=0时，f(0)min=-1(舍去)；②当0＜t≤1，s=t时，③当t＞1，s=1时，，可得(舍去)。综上可得

三、与三角形的心的交汇问题

例3 若点O，H分别是△A B C的外心和垂心，求证

解：如图1，延长B O交圆O于D，则B D为圆O的直径，故∠B C D=∠B A D=90°。延长AH交B C于E，因为A E⊥B C，所以AH∥D C。同理可得，DA∥CH，所以四边形AHC D为平行四边形，所以

四、与概率的交汇问题

例4 将一颗骰子投掷两次分别得到点数a，b，则向量c=(a，b)与向量d=(-1，1)的夹角θ＞90°的概率是( )。

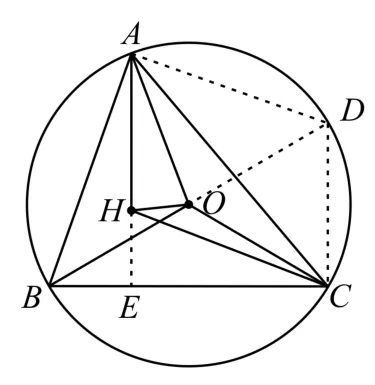
图1

解：由向量c=(a，b)与向量d=(-1，1)的夹角θ＞90°，可得-a+b＜0，即a＞b。一颗骰子投掷两次分别得到点数(a，b)的所有基本事件为(1，1)，(1，2)，…，(6，6)，共36种情况，其中a＞b的共有(种)情况。故所求概率为应选D。

例5 已知G为△A B C的重心，过点G的直线与边A B，A C分别交于点D，E，现将一粒黄豆随机撒在△A B C内，若则黄豆落在△A D E内的概率为____。

解：设由G为△A B C的重心，可得由D，G，E三点共线，可得由此可得解得。故所求概率为