三角恒等变换综合演练B卷

■卜素英

一、选择题

1.已知角α的顶点为坐标原点，始边与x轴的非负半轴重合，终边过点P(3，4)。若角α，β满足tan(α+β)=2，则tanβ=( )。

2.已知，则

3.下列数值最接近的是( )。

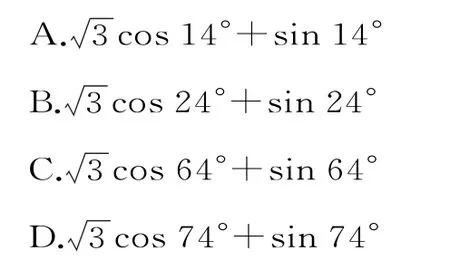
4.已知函数f(x)=sin(sinx)+cos(sinx)，x∈R，则下列说法正确的是( )。

A.函数f(x)是周期函数且最小正周期为π

B.函数f(x)是奇函数

C.函数f(x)在区间上的值域为

D.函数f(x)在区间上是增函数

5.若α，β均为锐角，且，则

6.若α，β为锐角，且则( )。

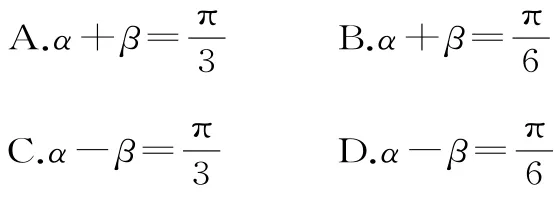
7.若则实数m的值为( )。

8.已知 3 π＜θ＜4 π，且，则θ=( )。

9.设，且tanα=，则下列结论中正确的是( )。

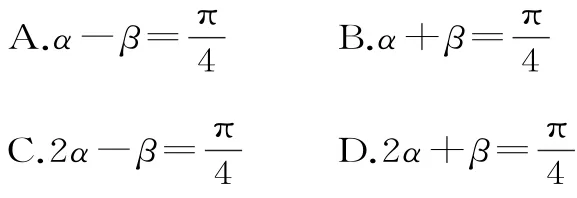
10.已知α为第二象限角，且tanα+等于( )。

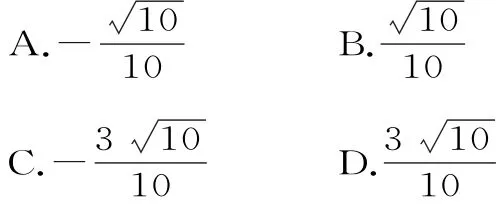
11.函数y=sin2x+2sinxcosx+的单调递增区间是( )。

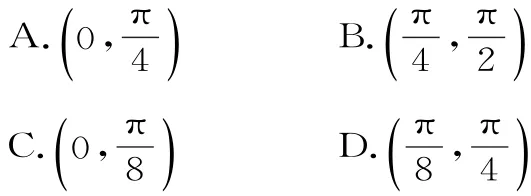
12.若s，且则α+β的值是( )。

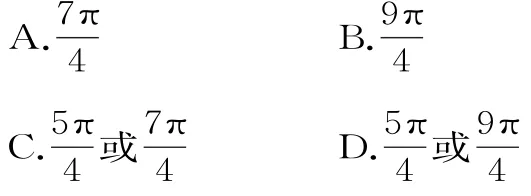
13.设，且tanα=

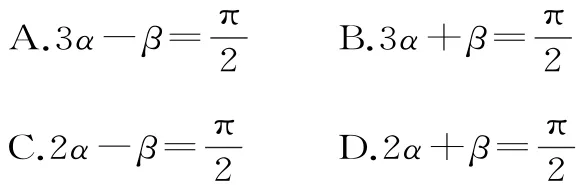
14.定义( )。

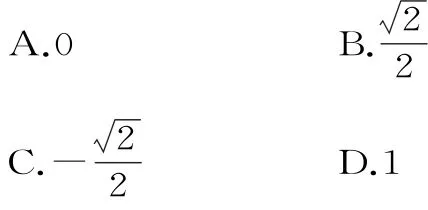
二、填空题

15.(1+tan 20°)·(1+tan 25°)=____。

16.第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的。如图1所示，会标是由四个全等的直角三角形与一个小正方形拼成的一个大正方形。

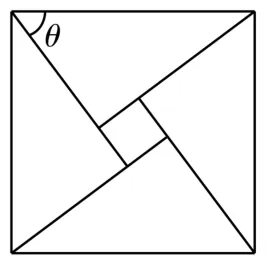
图1

如果小正方形的面积为1，大正方形的面积为25，直角三角形中较大的锐角为θ，那么

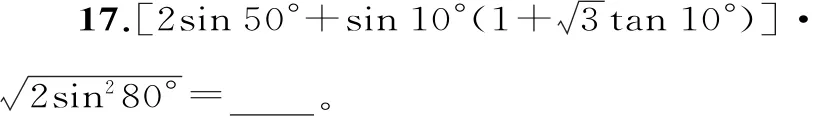
18.已知函数cosω x(ω＞0)。若函数f(x)的图像关于直线x=2 π对称，且在区间上是单调函数，则ω的取值集合为____。

19.设α，β都是锐角，且

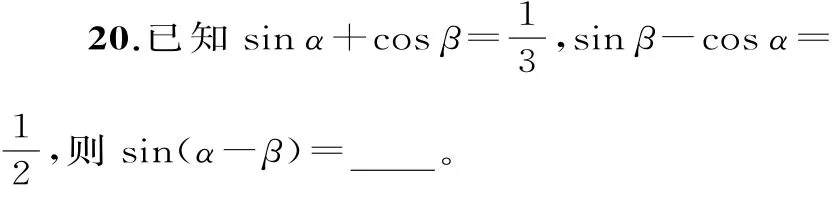
21.已知，则cos(α+β)的值为____。

22.若则

23.函数f(x)=sinx+cosx+2sinx·的最小值是____。

24.已知

25.已知函数f(x)=cos 2x+sinx，若对任意实数x，恒有f(α1)≤f(x)≤f(α2)，则

26.已知α，β均为锐角则cosβ=_______。

27.定义运算若则β=____。

28.已知则tan(α+β)=____，

三、解答题

31.已知函数

(1)求函数f(x)的定义域。

(2)设β∈ (0，π)，且f(β)=求β的值。

32.已 知 向 量a=(1，2sinθ)，b=

(1)若a⊥b，求tanθ的值。

(2)若a∥b，且，求θ的值。

33.已知函数的最小正周期为π。

(1)求函数f(x)的单调递减区间。

34.已知函数cos2ω x+b+1。(1)若函数f(x)的图像关于直线对称，且ω∈[0，3]，求函数f(x)的单调递增区间。

35.已知函数

(1)求函数f(x)的最小正周期及在区间上的最大值和最小值。数f(x)有且只有一个零点，求实数b的取值范围。

36.已知

(1)求cosα的值。

37.设，满足

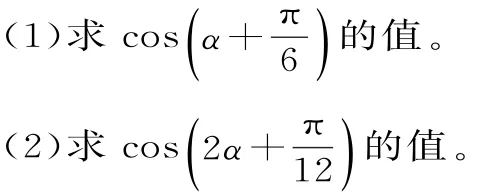
38.设函数f(x)=2 cosx(cosx+

(1)求函数y=f(x)的周期和单调递增区间。

(1)若函数y=f(x)的图像关于直线x=a(a＞0)对称，求a的最小值。

39.已知函数f(x)=2=0成立，求实数m的取值范围。