基于赫兹接触理论的核桃破壳分析与试验研究

2020-05-25郑甲红霍启新赵佳龙

西南农业学报 2020年12期

王超，郑甲红，霍启新，赵佳龙

(陕西科技大学机电工程学院，陕西西安 710021)

【研究意义】核桃又名胡桃、羌桃，属胡桃科胡桃属植物，与扁桃、腰果、榛子并列为世界四大干果[1]。核桃营养丰富，食用价值高，是一种集脂肪、蛋白质、糖类、膳食纤维、维生素五大营养要素于一体的优质坚果，已成为我国重要的木本油料树种之一[2]。破壳作为核桃深加工的重要环节，不仅技术要求高，而且直接影响核桃的后续加工质量。【前人研究进展】国内外核桃破壳装备采用的破壳技术主要有化学腐蚀破壳法、真空破壳法、超声波破壳法、机械破壳法。机械法破壳包括击打式、挤压式、滚压式离心式和剪切式[3]。挤压式和击打式的破壳方式的接触面主要是平面，如Michael 等发明的一种凸轮击打式核桃破壳机、Eisel发明的平板挤压破壳机构以及王亚雄等人研究的多点挤压式核桃破壳机[4-6]，辊压式的挤压面是圆弧面如Kim研制的单棍子挤压破壳机构[7]，McSwain发明的双辊子滚动挤压式破壳机构[8]，以及朱德泉等设计的6HS-6型山核桃破壳机[9]，另外塔里木大学郭文松等人研制的尖点辊压式核桃破壳机。尖点对辊破壳装置在对置辊上布置尖点钉以实现更好的破壳效果[10]。【本研究切入点】目前还没有学者在使用挤压破壳原理破壳时，对与核桃接触的表面的最优曲率半径做出研究。【拟解决的关键问题】本文基于赫兹接触理论在4点破壳机构，设计出挤压面的最优曲率半径，以提高核桃破壳的整仁率和高露仁率。

表1 核桃物理参数

1 材料与方法

1.1 核桃物理参数的测量

本次随机选取200个陕西香玲核桃，对各个物理参数进行了测量，其中长径、短径、棱长、壳厚为直接测量的结果，间隙和球度是计算得到的结果，然后根据测量结果对核桃进行了分级，参数如表1所示。

1.2 数据分析

如表1所示，I级核桃的核仁间隙最小，间隙为2.44 mm；II级别的核仁间隙为2.88 mm；III级别的核仁间隙最大，间隙可达3.54 mm。3个及级别的核桃壳厚在1.42～1.50 mm，差别很小， II级的核桃占核桃总量的比例最大，是破壳的主要研究对象，此外除了核桃的尺寸大小因素不同之外，其他的物理参数差别并不明显，因此选择II级的核桃作为建模对象。

1.3 设定三维坐标系

本文为方便后边的对核桃的表述，对核桃的三维尺寸进行定义，如图1所示，以核桃的中心建立坐标系，以核桃的缝合线方向为X轴，垂直于核桃的缝合线的位置为Y轴，核桃的长轴为Z轴。

图1 核桃的简化模型

1.4 计算接触面曲率半径

挤压破壳原理是接触体和核桃相互接触挤压，使核桃壳破碎来达到取仁的效果，接触应力随着外载荷的变化而变化，还与接触体的边界条件、刚度以及曲率半径有关，研究核桃外壳的力学性能，需要将其纳入线弹性的范畴，因此需满足材料的各向同性、弹性变形和微小变形3个基本假设[15]，赫兹接触理论是研究两物体间因外部载荷而相互挤压产生的接触应力的分布规律。核桃在被挤压过程中，会经过弹性变形、塑性变形和突然破裂3个阶段[16]。基于弹性的赫兹接触理论一般假定:①接触系统由两个相互接触的物体组成，物体之间不发生刚体运动；②接触变形为小变形，接触尺寸远小于物体尺寸；③接触表面光滑且作用力垂直于接触面；④变形处于弹性范围内；⑤不考虑接触面的介质，不计动摩擦影响[17]。

由表1可知，核桃的球度都在90%以上，因此核桃和接触面相互挤压可以看成是赫兹接触理论中的2个球体相互接触，是典型的线性接触问题，接触体承受法向荷载后，接触体在接触线附近产生变形，从而形成直径为2a的圆形挤压区域，接触最大应力分布在接触面中心法线上，其余各点接触应力按圆形分布。(1)式为赫兹接触应力两球体接触的挤压区域半径公式。

(1)

II级核桃的球度为0.95，因此将核桃近似为球体进行计算，核桃的直径为 34 mm，壳厚1.43 mm，核仁间隙为2.88 mm，由于I级核桃的核仁间隙为2.44 mm，核仁间隙最小，因此设计的时候核仁间隙应该按照I级核桃来计算，简化模型为图2-a，核桃壳和核仁的几何关系为图2-b，图2-c是核桃和接触面发生挤压时核桃和接触面的状态简图，R1为核桃的曲率半径，R2为接触面的曲率半径，a表示核桃和接触体的挤压区域半径，b表示核桃仁的半径，c表示核桃的外径，挤压时，核桃的最大挤压区域所在的平面不能接触到核仁，根据图2-b的几何关系，可得核桃的最大破坏直径:

图2 核桃接触简化模型

(2)

因此，

(3)

通过在万能材料机上的破壳试验可知：核桃的最大破壳力为250 N，因此P=250 N。取核桃半径R1=17 mm,μ1=0.29,E1=13100 MPa[18,20]，接触面μ2=0.3，E2=206 GPa。

解(3)式得R2≤-17 mm，因此核桃和接触面的接触为凹球面接触，接触时候的状态简图为图2-d，由于挤压时不能伤到核仁，就要保证接触面的弧顶不能接触到核仁，因此可以得到式(4):

(4)

将数值带入利用MATLAB解出该方程的结果为R2≥33.64 mm。

根据挤压半径算的R2≥33.64 可以达到不伤害核桃仁，令f(R2)=a3

(5)

所以f(R2)单调递减，而挤压区域的半径在不伤着核仁的情况下越大越好，所以接触面的最佳曲率半径R2=33.64 mm。

2 结果与分析

2.1 最佳集中应力对数的分析

2对集中应力的作用下，外壳作用点的位移最大，也说明壳中产生的内力最大，外壳容易发生破裂[21]，因此本次建立的接触模型的对数也是2对接触体作用在核桃壳体上。

2.2 接触模型的建立

为了降低碎仁率，本文对核桃壳体创建了3种不同的接触体，如图3所示，其中，图3-a表示平面和核桃发生挤压破壳，图3-b表示凹球面和核桃发生挤压破壳，图3-c表示尖点和核桃发生挤压破壳，分别对于每个接触体轴向施加250 N的力，在ANSYS workbench中得到需要的云图来验证不同曲率半径的接触面对于核桃的挤压破壳效果，从而得到最优的接触面的曲率半径。

2.3 3种不同接触体的仿真

2.3.1 材料属性的定义核桃壳的材质类似于木材，在定义材料属性时，核桃的弹性模里取13 100 MPa，泊松比0.29，密度470 kg/m3，将模型导入以后，接触体的材料定义为结构钢，其参数取默认值。

2.3.2 网格划分有限元分析的关键一步是网格划分，对分析结果影响很大[22]，将模型导入以后对其进行自由网格划分生成有限元模型，核桃接触体的节点数9447，单元数为4990。

图3 3种不同的接触体

2.3.3 施加载荷和约束破壳的最佳位置为：1对接触体在Y=X方向，一对接触体在Y=-X方向[5]，下面来研究不同接触面对核桃的破壳效果的影响，第1种接触面是平面，第2种是通过赫兹理论计算出来凹球面，第3种接触面是尖点，3种不同的接触面和核桃的装配边界条件设置如图4所示，图4-a中核桃的接触表面为平面核桃的Z轴施加Fixed Support，接触体的外圆表面添加Cylindrical Support，设置轴向可以移动，径向和切向固定，使得接触体在施加的力的作用下可以沿着接触点向核桃的中心挤压，在4个接触体的轴向分别添加250 N的力，指向核桃中心，接触类型设定为No Separation。第2和3种接触体的边界条件设置方式和第1种完全一致。图5～7分别是接触面为平面、凹球面和尖点的变形、应变、应力云图。

2.4 接触面为尖点时变形应变应力分析

从图7可以看出，尖点挤压的核桃，核桃表面虽然应力大，但是应力分布面积非常小，变形云图上可以看出，变形面积也非常小，因此可以判断出核桃挤压以后大多数不会整体开裂，而是和接触位置对应，在接触位置开出有很小的面积被压溃，从图5～7的

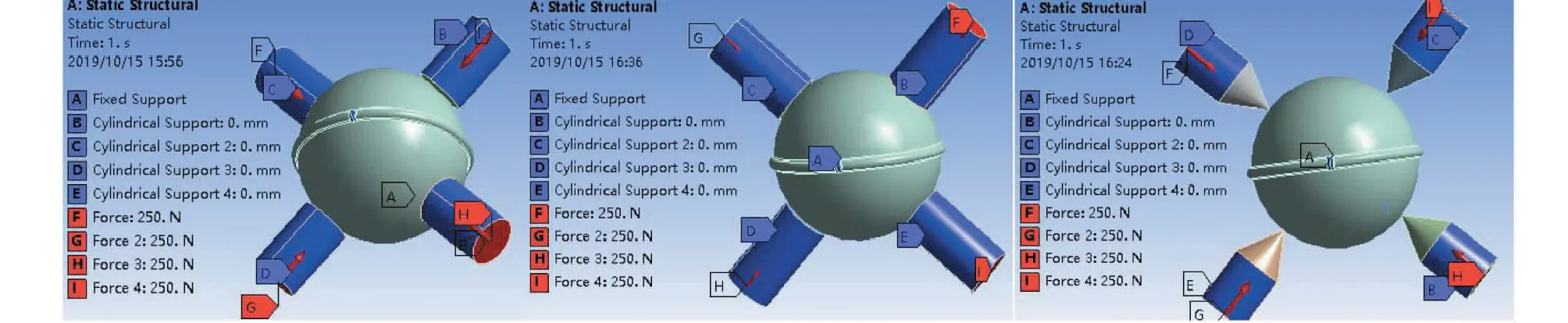
图4 不同接触体的边界条件设置

图5 接触面为平面时核桃的变形、应变和应力

图6 接触面为凹球面时核桃的变形、应变和应力

图7 接触面为尖点时的变形、应变、应力云图

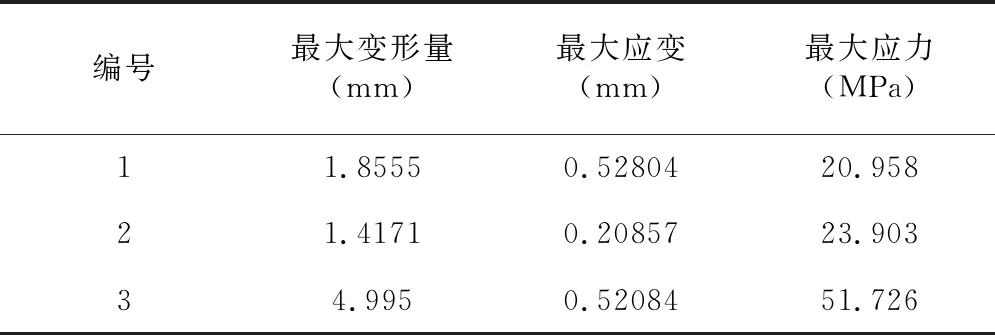
表2 仿真数据

比较中可以看出，凹球面挤压核桃时，核桃壳表面的变形面积更大。接触面为平面的挤压效果次之，接触面对尖点的效果最差。

表2为3种接触体的仿真数据，编号1为接触面为平面的数据，编号2为接触面为凹球面的数据，编号3为接触面为尖点的数据，最大变形量最大应变是3>1>2，最大应力是3>2>1，方案3由于接触表面是尖点，虽然最大应力、最大变形量大，但是根据应力云图来看，变形量和应力云图面积分布都比较小，所以很容易伤害到核仁，而且会导致破壳不完整，并且压溃面积太小，导致露仁率太低，方案1和方案2的数据相比较，方案2的变形和应变小于方案1，但是方案2的应力分布面积大于方案1，最大应力方案2大于方案1，因此方案2的接触类型更有利于核桃壳的整体开裂。

综合仿真数据，以及云图分析，曲率半径为33.64 mm的接触面对核桃的破壳效果最好。

2.5 实验设计

2.5.1 试验设备与材料试验所用设备为自制的多点挤压式核桃破壳试验台如图8所示，所需要的仪器如表3所示。

如图8所示，法兰固定在机架面板上，法兰中间孔为单个核桃进料口，法兰里面设置核桃支撑垫块，核桃从进料口下来可以定位，法兰四周安装4个无油衬套，导向轴在无油衬套中往复运动，导向轴靠近法兰一侧安装有接触接头，用于挤压核桃，接触接头设计3种形式，第1种接触面是平面，第2种接触面是凹球面，第3种接触面近似一个尖点，导向轴远离法兰一侧连接滚轮支架，用于安装滚轮，由于复位弹簧作用，滚轮与滚道圆盘相互接触，滚道圆盘内圆面有缺口，滚轮初始位置在滚道圆盘切口最深的圆弧处，逆时针转动把手，导向轴向靠近法兰的方向移动，此时接触接头挤压核桃，当核桃挤压完成时，在弹簧的作用下复位。

表3 仪器设备参数表

2.5.2 试验指标核桃破壳的时候主要是核桃的整仁和核桃破壳的完整情况，本文采用加权评分方法将破壳率P、整仁率Z和高露仁率G3个指标进行综合计算，将所得到的综合评价值Q作为试验指标，破壳率：将核桃壳的破碎率达到总面积3/4以上的核桃数量和总核桃数量之比；高露仁率：破壳后1/4及以上大小的核桃仁质量占总试验核桃仁质量之比；整仁率：整仁的质量占破壳后得到核仁的总质量之比，公式为：

(6)

式中，P：破壳率；G：高露仁率；Z：整仁率；KP：每组试验中大部分被完全挤压破壳的核桃个数；KZ：每组核桃总数；Rg：每组试验中所得到1/4仁及以上的核桃仁质量；RZ：每组试验中所得到核桃仁的质量；Zg：每组试验中所得到的完整的核桃仁质量；Q：核桃评价指标。

1.滚轮，2.滚道圆盘，3.螺栓，4.滚轮支架，5.把手，6.复位弹簧，7.导向轴，8.接触接头，9.法兰，10.支撑垫块，11.无油衬套，12.机架面板

表4 试验因素及水平表

2.5.3 试验方法为了研究不同接触面对于核桃破壳的影响，本次试验对核桃进行浸泡，使其达到规定的含水率，调节3种接头的位置来调节核桃挤压破壳的行程，替换3种不同的接头来测试不同接触面对核桃破壳的影响。不考虑交互作用，研究各个因素与破壳效果之间的关系，选出最佳的工作参数，得出不同接触面在不同的含水率和挤压行程的作用下对核桃破壳的影响。

以综合评价值Q作为试验指标，考虑到含水率，挤压行程，以及不同的接触表面对于核桃的影响，因此选择这3个因素进行L9(34)正交试验。正交试验共进行9组，每组选用30个核桃进行破壳试验，试验因素水平表如表4所示。

2.5.4 试验结果及分析由表5可以看出，影响破壳效果Q的因素主次顺序为C接触面类型、A含水率、B挤压行程，在K值中K2A、K2B、K2C的相对最大，所以破壳效果最好的是A2、B2、C2，由极差分析可以看出，影响核桃破壳效果总值的主次顺序是C、A、B，所以破壳的最优方案是C2A2B2。

2.5.5 方差分析本试验为三因素三水平的正交试验，不考虑交互作用，在进行正交试验后，对影响核桃破壳效果的3个因素指标进行方差分析[23]，首先选择置信度为90 %，如表6所示，经过分析得出：3个因素中，对于试验结果影响最为显著的是接触面类型，而含水率和挤压行程对于破壳效果不显著。

2.5.6 效应曲线图如图9所示，含水率为20 %的时候破壳效果最好，行程为6 mm的时候效果最好，a、b、c分别表示接触面为平面、凹球面、尖点，接触面为凹球面时破壳效果最好，平面的曲率半径为∞，尖点的曲率半径接近0，无法确定33.64 mm附近还有没有最优解，因此进行了3组最优条件试验和3组接触面曲率半径的试验，试验结果如表7所示。

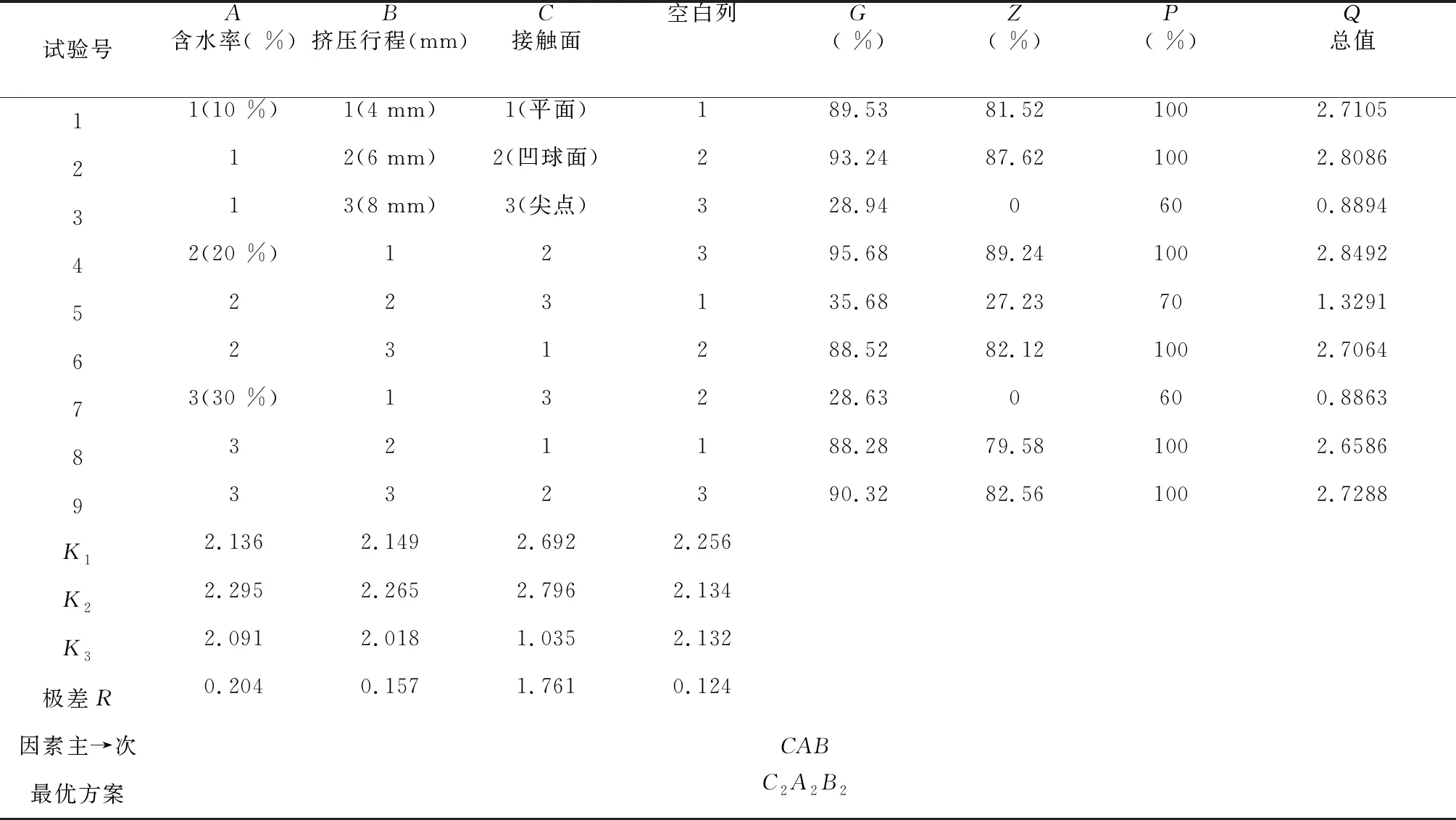
表5 正交试验设计与结果

表6 方差分析表

表7 验证试验结果

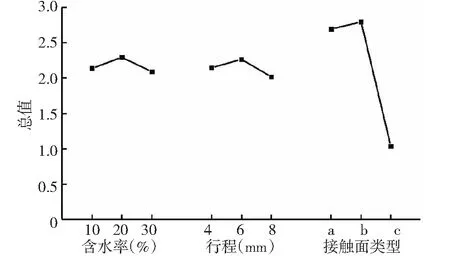
图9 效应曲线图

2.5.7 验证试验根据正交试验得到，最好的因素条件为A2、B2、C2，即含水率20 %，行程6 mm，接触面曲率半径为33.34 mm的凹球面，为此重新做了3组不同曲率半径的接头，分别为-50、-20、20 mm(凹球面曲率半径取-，球面曲率半径取+)来验证试验，由表7可知，前3组为最佳因素，3组试验结果较为接近，后3组试验为不同的接触面曲率半径的试验结果，在-33.64 mm附近取的3组值试验结果表明，明显不如前3组，破壳效果相对较差。