小型开架式水下机器人水动力特性仿真研究∗

程啸鹏 胡 桥 和岩辉

（1.西安交通大学机械工程学院 西安 710049）

（2.西安交通大学机械制造系统工程国家重点实验室 西安 710049）

（3.陕西省智能机器人重点实验室 西安 710049）

1 引言

小型开架式水下机器人具有航行机动灵活、续航时间长、环境适应性强等特点，被广泛应用于水下检测、勘探等领域，是人类探索海洋的重要工具［1］。机器人在水下航行过程中水动力复杂难以预测，水动力系数的准确获取直接关系到动力学控制模型的建立和机器人的操纵性［2］。因此为保证机器人在水下航行的稳定性和精确性，必须先获取其相关水动力系数。

目前获取水动力系数的方法主要有以下四种:约束船模实验、经验公式估算、CFD仿真计算、系统辨识［3］。2013 年，FAN Shi-bo［4］使用大振幅水平面运动机构完成了针对4500m 深海ROV 的水动力系数测量。2017年，Petit［5］基于CFD软件模拟AUV沉浮运动，并求解出相应的水动力系数，用于AUV 深度控制。2018 年，S Zhang［6］通过水池振荡模型实验，获得了相关水动力的附加质量系数和阻力系数，并建立了相关数学模型。经验公式法常应用于鱼雷、船舶水动力系数估算，小型开架式水下机器人由于外形复杂、附体较多，所以误差较大［7］。系统辨识法常用于水动力后期修正，不适用于前期水动力系数获取［8］。约束船模实验虽然可靠且准确，但试验耗资大、周期长，不利于小型水下机器人的开发和研究［9］。随着计算机流体力学的发展，CFD仿真计算为水动力系数的获取提供了一种新的方法和手段［10］。

目前CFD仿真计算还处于初步应用阶段，大部分研究仅停留在直航运动相关水动力系数的获取，关于水动力和角度、加速度之间的关系，还有待进一步研究［11］。本文提出了一套完整的基于CFD 仿真获取水动力系数的方法，旨在解决传统方法的弊端。同时利用FLUENT 软件在计算机上模拟完成了相关约束船模试验，探究了水动力与速度、角度以及加速度之间的关系，得到了相关水动力系数。仿真结果将为后续运动控制和操纵性分析提供参考依据。

2 水动力理论分析

2.1 惯性类水动力

机器人航行过程中会克服流体惯性产生一种惯性类水动力。由于水下机器人存在着耦合，某一轴的惯性类水动力，包括该轴向运动产生的惯性类水动力和其他轴向运动惯性类水动力在该方向的分力［12］。若惯性类水动力比例系数为λij，则某个方向的惯性类水动力为

式中:i，j取1～6，即1、2、3 对应X、Y、Z轴的移动，4、5、6 为X、Y、Z轴的旋转，Fj（j=1～6）分别代表XI，YI，ZI，KI，MI，NI；U˙（i=1～6）分别代表u˙、v˙、w˙、p˙、q˙、r˙。

惯性类水动力系数矩阵如下:

本文所研究的“XJTU 号”机器人上下、左右、前后基本对称，故只剩下对角线6 项惯性类水动力系数即λ11、λ22、λ33、λ44、λ55、λ66。

2.2 粘性类水动力

粘性类水动力是机器人在运动过程中克服流体粘性产生的力以及力矩［13］。考虑到机器人对称性特点，可以将机器人粘性类水动力分别按照水平面运动和垂直面运动分别推导。将水动力用多元泰勒级数展开，可得到相应的粘性水动力计算表达式［14］。考虑到机器人的对称性，可将表达式进一步简化。得到如下表达式:

水平面运动时粘性水动力为

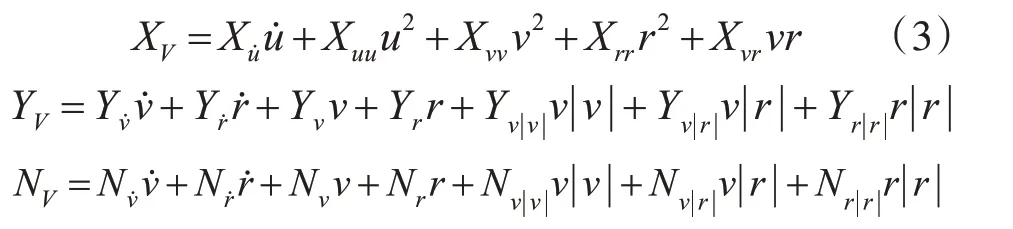
垂直面运动时粘性类水动力为

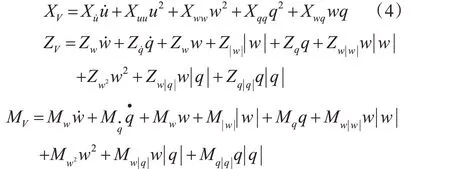
式中:XV、YV、ZV、NV、MV为X、Y、Z 方向，以及绕Z、X 轴转动粘性力及力矩；u、v、w、p、q、r 为X、Y、Z 方向速度，以及绕Z、X 轴转动角速度；Xu˙、Yv˙、Nv˙、Xuu等为相关水动力系数。

3 基于FLUENT仿真建模

本文所验证计算的模型“XJTU 号”为小型开架式水下机器人。利用FLUENT 前处理软件GAMBIT 严格按照1:1 比例建模，并对模型进行适当简化，剔除掉部分极小的不规则壳体，在不影响结果的情况下，减小计算时间。模型尺寸为380mm×330mm×220mm，如图1所示。

为模拟“XJUT 号”在水下航向实际状态，外流场尺寸为2000mm×1200mm×1000mm，将“XJTU 号”添加到外流场中心区域，机器人与外流场相对位置如图2所示。

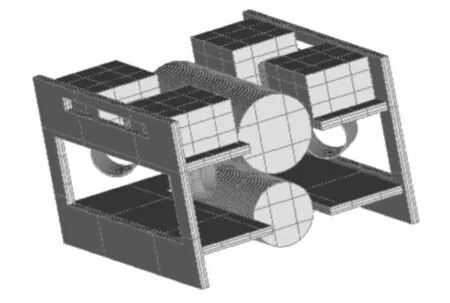
图1 “XJTU号”实体模型

图2 外流场与机器人相对位置图

采用三角形非结构化网格单元对外流场和机器人进行网格划分，并将机器人外表面进行局部加密，“XJTU 号”网格图如图3 所示。经过反复计算和试算，最终模型网格总数为1338646，其中机器人外表面最小单元尺寸为0.1mm，Quality 大于0.8网格占比约为90%。

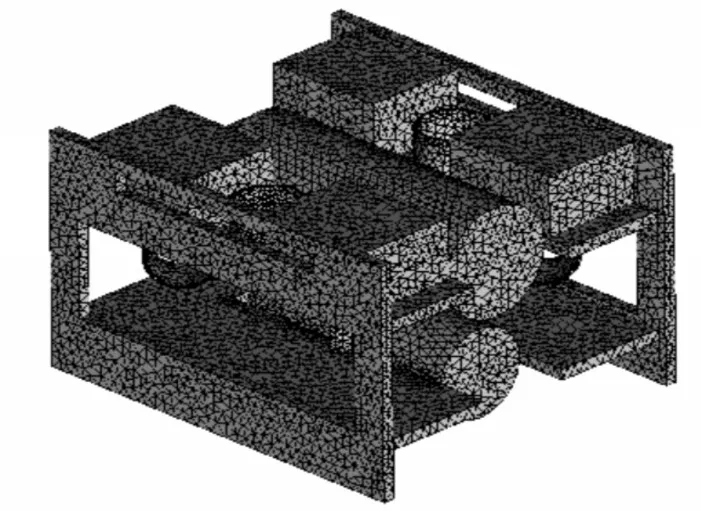
图3 “XJTU号”网格图

4 水动力特性仿真实验

本节将基于FLUENT 模拟机器人直航、斜航以及加速直航运动实验，研究水动力和速度、角度、加速度之间的关系。

4.1 速度对水动力的影响

直航水动力模拟实验中只有速度项而没有加速度项，故可以忽略惯性类水动力产生的影响，只保留主方向与速度相关的水动力即可。本小节模拟“XJTU 号”在不同速度下，进退、横移、沉浮所受的水动力，具体直航不同速度下水动力仿真数据见表1。

表1 不同速度下水动力表

利用最小二乘法进行幂函数数据拟合，可得水动力大小与速度之间关系表达式如下:

其中，Y为“XJTU号”直航过程中所受到的水动力，x为“XJTU号”航行速度。

分析数据可知:

直航时，同一方向上，水动力大小随着速度增大而增大，且大致呈二次函数关系。

4.2 漂角对水动力的影响

漂角是水下机器人在水平面斜航运动的偏移水动力角。模拟不同漂角下“XJTU 号”水平斜航实验，攻角默认为0。首先模拟速度为0.25m/s 下，漂角在［-90°～90°］区间内，每隔15°变化下水动力实验，具体水动力结果见表2。

如图4 所示，纵向力明显大于横向力，且纵向力和总阻力关于Y 轴对称，横向力关于原点对称。为进一步研究不同漂角下水动力变化规律，将设置对照实验，由于水动力关于漂角具有对称性，对照实验将只研究漂角在［0°～90°］范围内水动力变化规律。

分析图5和图6，可知:

1）水平斜航时，纵向力关于Y 轴对称，横向力关于原点对称。纵向力在0°～45°范围内上升迅速，在45°～90°范围内波动。横向力在0°～45°上升，在45°～90°下降，45°时存在峰值。

2）通过数理统计可发现，同一漂角下，航行所受各方向水动力大小与速度平方成正比。

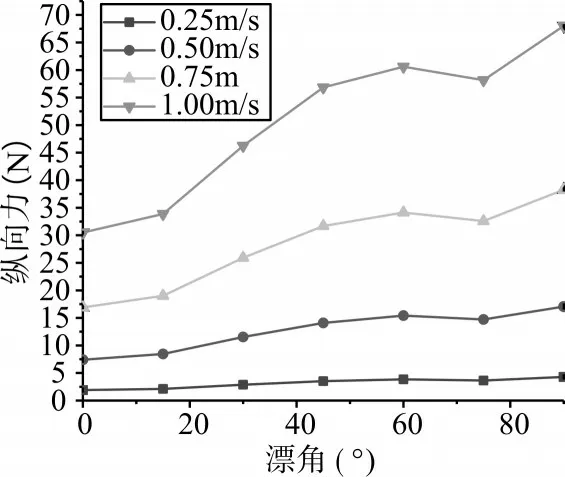
图5 不同速度下漂角纵向力曲线图

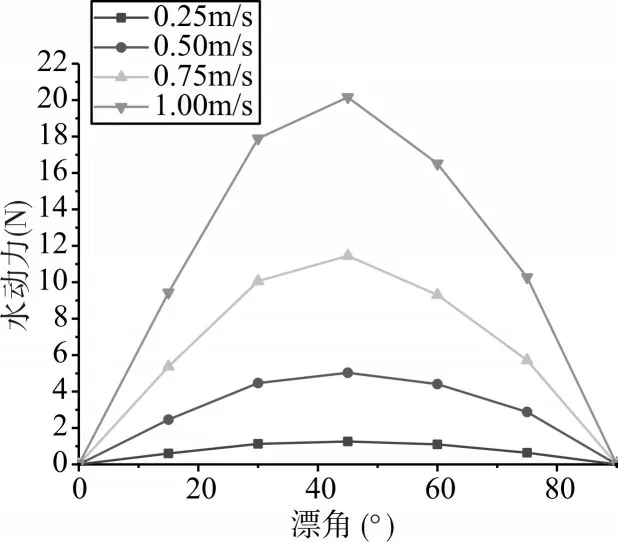
图6 不同速度下漂角横向力曲线图

4.3 攻角对水动力的影响

攻角是机器人在垂直面斜航运动的偏移水动力角。模拟“XJTU 号”在不同攻角下垂直面斜航实验，漂角默认为0。首先模拟机器人前行速度为0.25m/s 下，攻角［-90，90°］区间内，每隔15°变化下水动力随攻角的变化规律，具体水动力结果见表3。

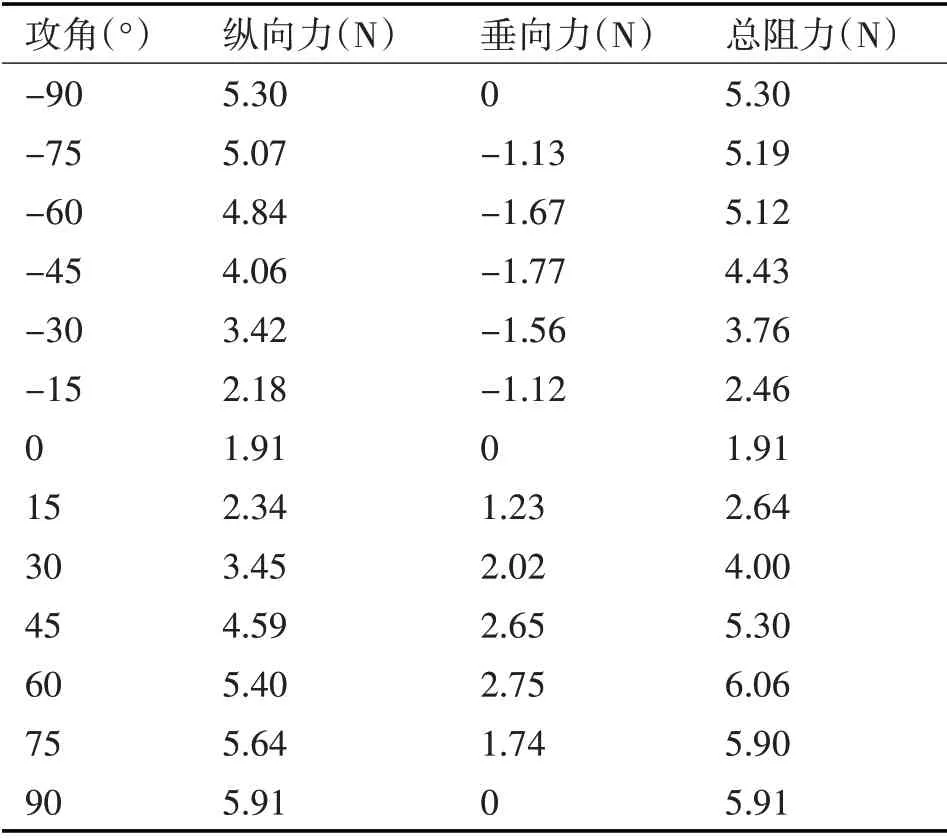
表3 0.25m/s不同攻角下水动力表

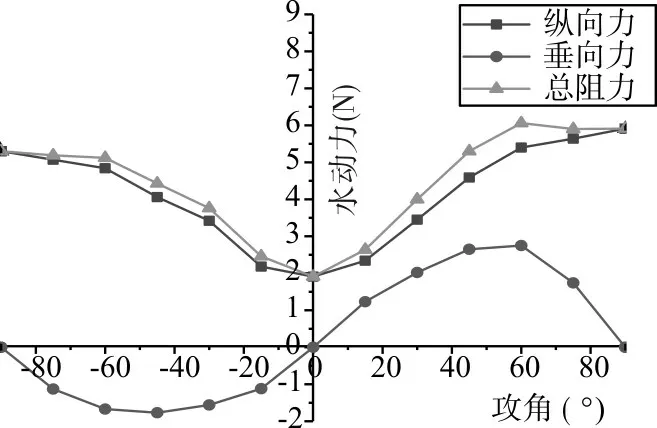
图7 不同速度下漂角纵向力曲线图

为进一步研究不同攻角下纵向力和横向力变化规律，将设置对照实验组。

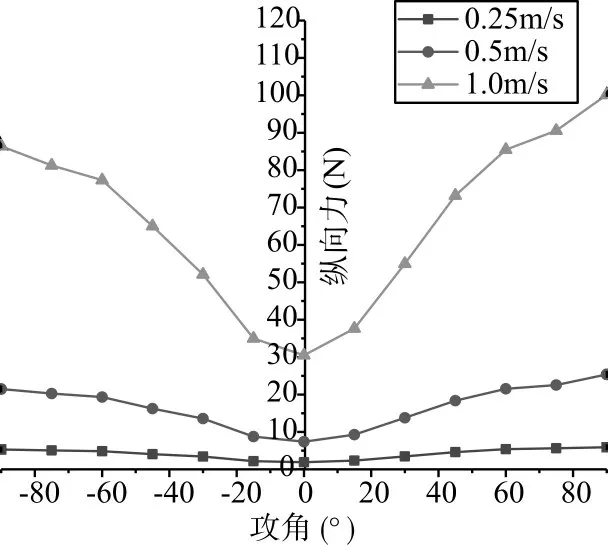
图8 不同速度下攻角纵向力曲线图

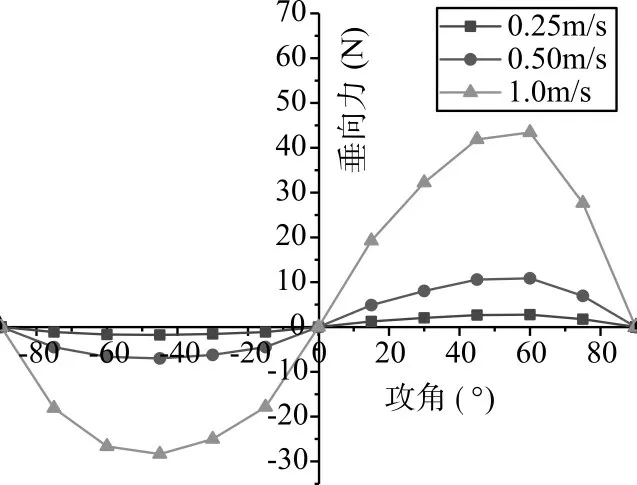
图9 不同速度下攻角垂向力曲线图

分析图8和图9，可知:

1）纵向力在0°～90°持续上升，90°为纵向力峰值。垂向力在0°～60°先上升，在60°～90°后下降，垂向力最大值出现在60°附近。

2）攻角绝对值相同时，攻角大于0 时的纵向力和垂向力明显大于攻角小于0 时的纵向力、垂向力。这是由于“XJTU 号”上表面布置有通水孔，能明显减小航向阻力。

3）分析数据可发现，同一攻角下，航行所受各方向水动力大小与速度平方成正比。

4.4 加速度对水动力的影响

本节将模拟机器人以0.25m/s2、0.5m/s2、0.75m/s2、1m/s2加速度横移、进退、潜伏五个方向加速运动，共20组矩阵对比试验。通过UDF编写入口水流的速度函数，加速运动总采样时间为4s，以0.01s作为单次采样时间，单次采样时间迭代200 次以保证阻力收敛。仿真数据如表4所示。

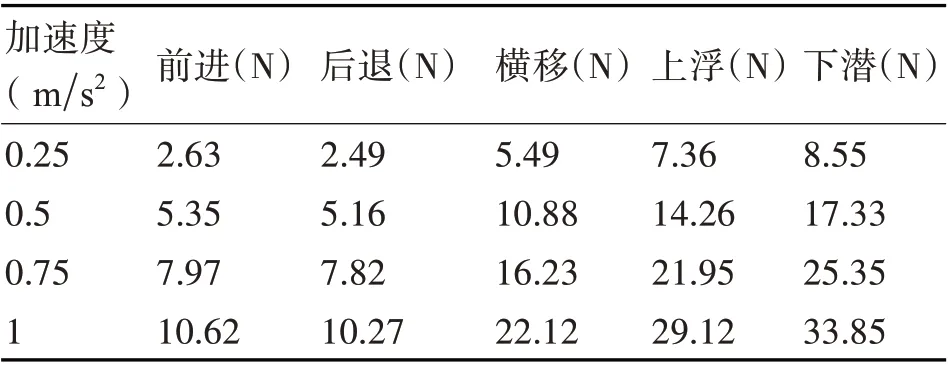
表4 不同加速度下惯性类水动力

同时利用最小二乘法将表4 数据进行数据拟合，可得惯性类水动力与加速度关系如下:

其中，I为各方向惯性类水动力、a为各方向航行加速度。

分析数据和拟合公式可知:

同一运动方向，惯性类水动力大小与加速度呈正比。

5 水动力系数对比分析

水动力系数是机器人水动力特性的量化指标，本节基于前文FLUENT 模拟实验结果，针对“XJTU号”水动力系数展开求解，获取精确的水动力系数，用于“XJTU 号”后续的动力学建模和运动控制研究。

其中，Xu||u、Yv||v、Zw||w为二阶速度水动力系数平均值，Xuu、Zww为二阶速度系数不对称修正值，Xu˙、Yv˙、Zw˙为附加质量系数，X||u˙、Z||w˙为附加质量不对称修正系数。

表5 水动力系数表

本文将选取与“XJTU 号”形状尺寸相仿的华中科技大学船舶与海洋工程学院微小型开架式水下机器人［15］直航拖曳实验获得的主要水动力系数Xu||u、Yv||v、Zw||w做对比。同时将水动力系数无因次化，统一两者尺寸量纲。具体对比结果，如表6所示。

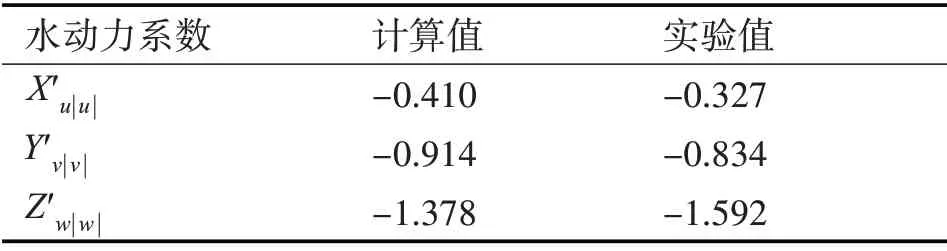
表6 水动力系数对比

“XJTU 号”与华中科技大学微小型开架式水下机器人外形虽然相近，但尺寸和外壳结构均存在差距，并且实验环境水流复杂，都会对水动力系数产生影响。

通过对比主要水动力系数Xu||u、Yv||v、Zw||w结果，可知“XJTU 号”仿真水动力系数与实验水动力系数处于同一数量级，且Y′v||v最小误差仅为8.7%。 总体来说，基于FLUENT 水动力特性仿真研究结果处于合理范围内，证明了本文通过CFD软件仿真研究小型开架式水下机器人水动力方法的有效性。

6 结语

本文提出一种基于FLUENT 的小型开架式水下机器人的水动力特性仿真实验方法，取得了如下成果:

1）基于FLUENT 完成了水动力仿真模型的构建。建立了水动力仿真相应的外流道及运动模型，并采用三角形非结构化网格对机器人和外流道进行网格划分，Quality 大于0.8 网格占比约为90%。

2）基于FLUENT 模拟机器人直航、斜航以及加速直航运动实验，探究了水动力和速度、角度、加速度之间的关系。直航实验得到了机器人水动力与速度之间的量化表达式，斜航实验剖析了机器人水动力与漂角和攻角之间的关系，加速直航实验求解出惯性类水动力与加速度之间的量化表达式。

3）水动力系数求解与对比分析。利用最小二乘法求解出水下安保巡逻机器人相应的水动力系数，进一步完善了运动控制模型。同时将仿真实验结果与实际实验结果对比，最小误差仅8.7%，证明了本文仿真结果的有效性。