利用常规直剪试验评价非饱和黄土抗剪强度*

高志傲 李 萍 肖俊杰 李同录

(长安大学地质工程与测绘学院， 西安 710054， 中国)

0 引 言

非饱和土在自然界广泛存在(沈细中， 2011)。土体强度劣化多是因为含水率升高引起，其根本原因在于水利边界条件的改变，导致土中吸力(水势)不平衡，进而驱动含水率变化。因此吸力是表达非饱和土状态的重要应力变量。工程中遇到的黄土常位于地下水位之上，属于非饱和土。众多学者提出非饱和土强度理论(Bishop et al.，1963； Fredlund et al.，1978； Vanapalli et al.，1996； Xu， 2004； 马少坤等， 2009； 郑国锋等， 2019)，这些理论都是在Terzaghi饱和土有效应力原理基础上的拓展，认为非饱和土抗剪强度是吸力的函数，测量非饱和黄土吸力成为研究非饱和黄土强度的技术关键。通过轴平移技术对三轴、直剪设备进行改进，可以完成土样抗剪强度与吸力的测试。轴平移技术是控制孔隙水压力，通过透水不透气的陶土板施加孔隙气压力，达到平衡状态时所施加的气压和孔隙水压之差即为吸力。由于陶土板进气值条件的限制，测量吸力范围有限，对较干的黄土不适用。同时利用轴平移技术测试吸力过程中，每个状态下需要几天甚至几十天才能达到水-气压力平衡，控制吸力条件下剪切速率慢，测试时间极长，对容器的密封性能和对试验人员的操作要求高，这些缺点极大地制约了其在工程中的应用(扈胜霞等， 2005； 申春妮等， 2010； 林涛， 2018)。

表 1 试验土样的基本物理指标Table 1 Basic physical indicators of test soil samples

有学者为了避免控制吸力测量抗剪强度的困难，将含水率代替吸力，提出非饱和土抗剪强度经验公式(边加敏等， 2010； 邢鲜丽等， 2015； 翟栋梁等， 2019)。由于不同种类土在相同含水率下对强度影响作用不同，即使同一地区，土的风化程度、孔隙结构、粒径级配也有不同，导致强度与含水率的关系不唯一。因此用含水率这一指标表达非饱和土抗剪强度较难普遍应用。目前0压力下土样的初始吸力的测试技术较为成熟，方法也较多。如张力计法、压力板法、滤纸法、介电常数法、电导率传感器法等(孙文静等， 2018)。众多学者对非饱和黄土0压力基质吸力研究已经积累大量试验数据，并且成果显著(刘奉银等， 2010； 吴元莉等， 2011； 刘新华， 2012； 李萍等， 2013； 朱立峰等， 2013； 刘茹， 2014； 刘蒙蒙， 2015； 杨益彪等， 2015； 郑娟等， 2015)。其中滤纸法尽管是间接测试方法，却是唯一一种测试全范围吸力的方法，且测试速度快，成本低。Leong et al. (2002)、Feuerharmel et al. (2006)通过滤纸法与其他方法对比，认为滤纸法测试结果具有较高的精确度。美国材料与试验协会也通过了滤纸法的测试规范(ASTMD5298-10)。唐东旗等(2012)、谷琪等(2016)、晁建红(2017)都采用滤纸法对黄土进行了土-水特征曲线的测试，获得较好的效果。但基于吸力的非饱和抗剪强度公式，采用的是一定压力剪切过程中的基质吸力，不是初始基质吸力。剪切过程中的吸力较难获得，这也制约了非饱和土强度理论在工程中的应用。Tang et al. (2018)探讨了利用常规直剪仪与0压力初始土-水特征曲线相结合估计非饱和土强度的可行性。根据目前的文献，用0压力土-水特征曲线预测非饱和土抗剪强度研究并不多见。

本文利用滤纸法测试重塑黄土0压力的初始吸力与一定压力下剪后吸力，常规直剪仪的固快剪测试抗剪强度。在Vanapalli抗剪强度模型的基础上，提出了一种简化的方法来评估非饱和黄土抗剪强度。利用控制吸力的非饱和直剪试验验证模型的正确性，本文方法可以节约大量测试时间，为工程实践提供新的非饱和土强度估计思路。

1 试验方案

1.1 黄土基本物理指标

测试土样选自甘肃黑方台Q3黄土。其主要的物理指标如表 1所示，其塑性指数仅为9.2%，根据规程GB5007-2011，该土样为粉土。采用激光粒度分析仪对土样粒度进行分析，颗粒级配曲线如图 1所示，黑方台黄土的粒度主要集中在 10～100iμm 之间，不均匀系数Cu=9.31，为不均匀土。曲率系数Cc=1.28，是级配良好土，土样粒径变化范围广，各组分含量分布均匀。由击实试验得该土样的最大干密度为1.71g·cm-3，最优含水率为17.0%。

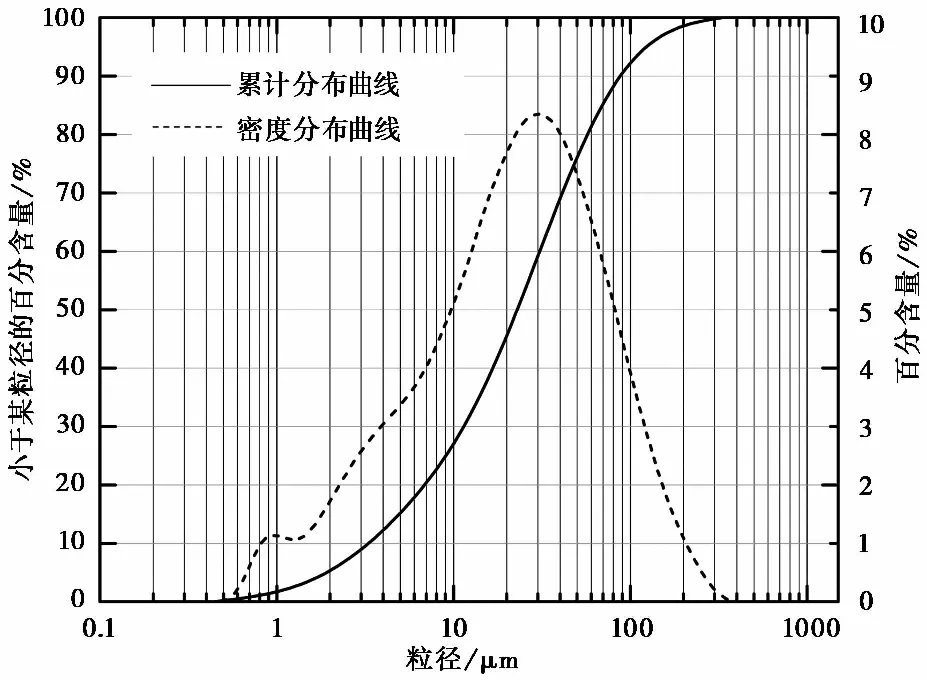
图 1 土样颗粒分析曲线Fig. 1 Soil sample particle analysis curve

1.2 直剪试验方案

将土样自然风干，过2imm筛，测定其风干含水率。加去气自来水配制成质量含水率为8%的土料，装袋放入保湿器24ih以上。

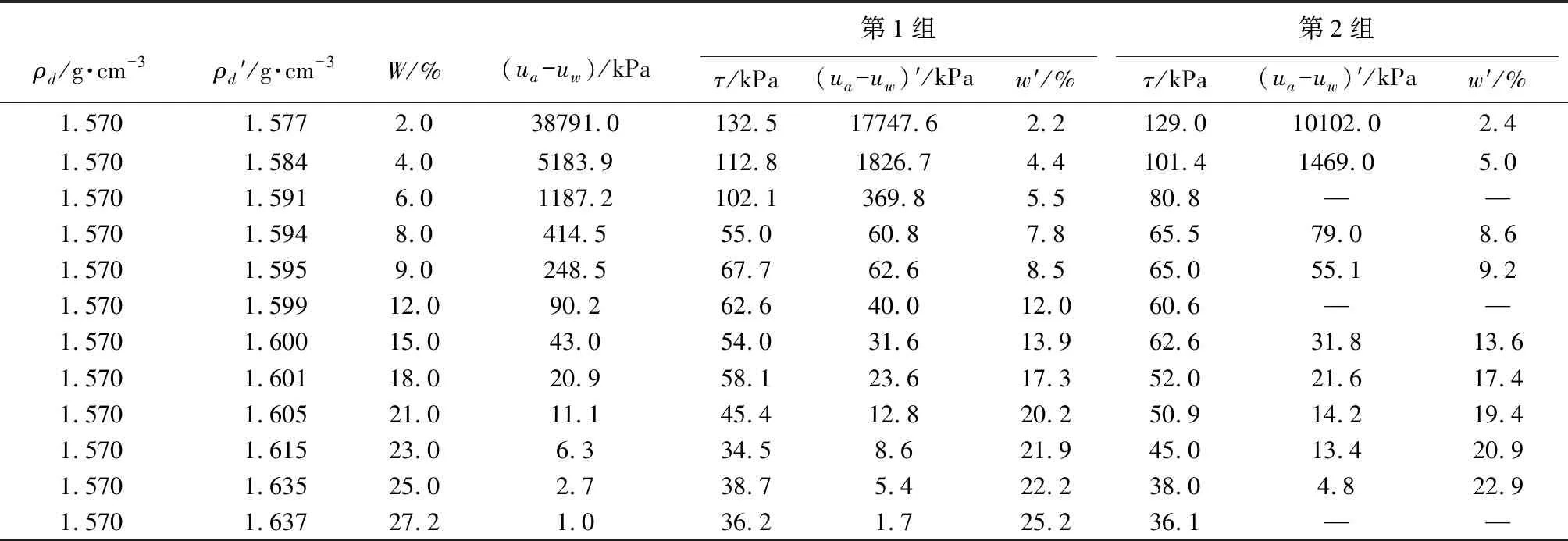
表 2 不同含水率下黄土的抗剪强度与吸力值Table 2 Shear strength and suction value of loess under different water content

ρd为初始干密度；ρd′为剪后干密度；w为初始质量含水率；w′为剪后质量含水率；τ表示抗剪强度；ua-uw为初始吸力； (ua-uw)′为剪后吸力通过压样器制备环刀土样多个，环刀高20imm，直径61.8imm。由于在击实曲线上8%含水率对应的干密度为1.57 g·cm-3，同时考虑到制样和测试过程中易于操作，保证剪后土样具有一定的完整性，最终采用了干密度为1.57g·cm-3的重塑土样和相应的制样含水率。采用滴定法加水或风干法减水，分别制备质量含水率为2%， 4%， 6%， 8%， 9%， 12%， 15%， 18%， 21%， 23%， 25%以及27.2%(饱和含水率)的试样，共12组，含水率采用称重法测量。塑料包裹配好水的环刀样，保湿器中保存3id，达到含水率平衡。采用的剪切速率为0.8imm·min-1和正应力50ikPa进行常规固结快剪试验。每个含水率土样都进行了并行测试，以消除试样过程中的变异性。

同样取4个干密度为1.57g·cm-3试样，控制吸力分别为10ikPa， 40ikPa， 80ikPa， 200ikPa，利用轴平移技术做非饱和直剪试验。使用50ikPa正应力恒定吸力条件下剪切。在剪切面上取土，烘干法测得剪后含水率。

1.3 初始和剪后土样吸力测试

对常规固结快剪的试样，进行了初始和剪后吸力测试。吸力测试采用接触型滤纸法。初始吸力每两个环刀一组，采用滴定法将提前准备好的烘干样，增湿称重，配水至不同预估含水率。待水分均匀后，将Whatman’s No.42滤纸夹在两张保护滤纸中间，并置于两个环刀样之间。保护滤纸直径稍大于中间的测试滤纸，保证测试滤纸接触不到土样，土样顶底面各放置1张含水率为土样含水率两倍的滤纸，多余的水分以便平衡中间干滤纸的吸水量。用电工胶带在上下土样接触处黏结好，将土样与滤纸固定在一起。用锡箔纸包裹土样，进行涂蜡密封。张贴好标签，放入20i℃恒温箱中平衡10id。剪后吸力每个环刀视为1组，将剪后土样取出，快速沿着剪切面切为两半，其间放置1张Whatman’s No.42滤纸，两张保护滤纸，同样土样顶底面各放置1张含水率为土样含水率两倍的滤纸，将滤纸与土样用锡纸包裹，同样进行厚层蜡封，张贴土样标签，放于20i℃恒温箱中平衡10id。通过测试平衡后滤纸含水率，利用ASTM(D5298-10)提供的率定方程可确定土样吸力值。公式见式(1)。黄土的常规直剪数据结果与吸力测量值整理于表 2。非饱和直剪测量数据整理于表 3。

表 3 非饱和直剪试验结果Table 3 Unsaturated direct shear test results

(1)

式中，ua-uw为吸力；wfp为滤纸含水率。

2 土-水特征曲线(SWCC)测试结果

将滤纸法测试吸力的对数值做横坐标，体积含水率为纵坐标，绘制吸力与含水率的关系(图 2)。初始体积含水率即为配置含水率，剪后含水率由剪后土样烘干法得到。初始吸力和剪后吸力与含水率的关系可用Fredlund et al.(1994)模型进行拟合，方程如公式(2)。

(2)

式中，ua-uw为吸力(kPa)； (ua-uw)r为残余体积含水率对应的吸力(kPa)；θs为饱和体积含水率(%)；a为与进气值有关的参数；n为基质吸力大于进气值之后与土体脱水速率有关的参数；m为与残余含水率有关的参数。Fredlund and Xing模型拟合参数见表 4，R2为相关系数。

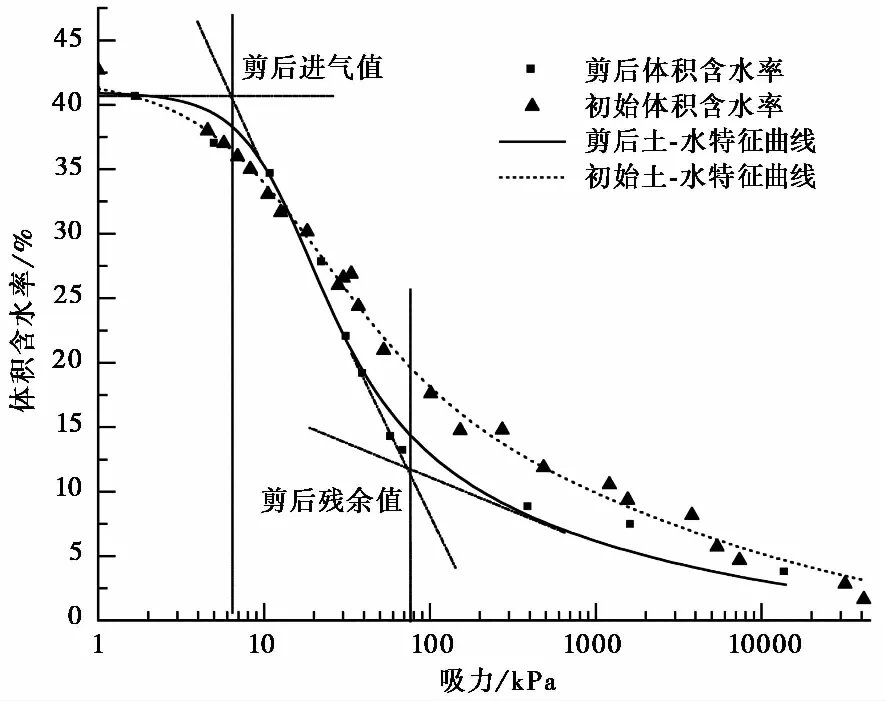
图 2 初始土样与剪后土样的土-水特征曲线Fig. 2 SWCC at initial and shearing state

表 4 SWCC参数拟合值Table 4 Fitting parameters of SWCC

同一土体在增湿和减湿过程中的土-水特征曲线是不同的，即相同吸力，土体在蒸发或者重力排水过程中赋存的水量比土体在入渗、毛细上升的吸湿过程中所赋存的水量多。本文初始土-水特征曲线配置不同含水率的方法，对于低于8.0%含水率土样，采用风干法减湿，高于8.0%含水率土样，采用滴定法增湿。因此同一条土-水特征曲线应该属于不同水化路径曲线。Fredlund et al. (2011)研究表明在含水率小于残余含水率时，增湿曲线和减湿曲线接近重合，滞后性可以忽略。依据表 4，本文测得的土-水特征曲线残余体积含水量为14.0%，对应的质量含水量为8.9%，接近制样含水量选用的8.0%，可见仅对8.0%以下的土样进行了减湿处理。因此可认为本文所测的曲线为增湿曲线。

目前的手段，仅能测定整个土样的吸力，较难测定局部剪切面上因为剪胀或剪缩导致的吸力变化，加之整体固结和排水导致的吸力变化，远大于剪切过程中导致的吸力变化，因此假定剪切过程中吸力值不变化，剪后吸力即认为是剪切过程中的吸力(Tang et al.，2018)。造成剪后吸力改变的因素较多，包括固结时土样孔隙变化、干密度变化等。剪后吸力与初始吸力关系如图 3所示。可将两者关系分为3个阶段。第1阶段，吸力大于残余值阶段，这一范围内剪后吸力小于初始吸力，经计算，该阶段初始吸力与剪后吸力差值与初始吸力比值的绝对值为0.65； 第2阶段，剪后吸力小于剪后残余值大于剪后进气值阶段，这一范围初始吸力与剪后吸力差值相对较小，可认为初始吸力能够代表剪后吸力； 第3阶段，吸力小于进气值阶段，剪后吸力大于初始吸力，初始吸力与剪后吸力差值与初始吸力比值的绝对值为0.65。

图 3 剪后吸力与初始吸力关系对比图Fig. 3 Comparison of the relationship between shearing suction and initial suction

干密度和饱和度两个因素影响着初始吸力与剪后吸力的对应关系。由于试验中竖向应力作用引起土样饱和度变化和干密度变化，剪后土样吸力发生改变。王铁行等(2008)、赵天宇等(2012)、褚峰等(2014)实测不同干密度黄土的土-水特征曲线，认为增大干密度，土样吸力增大； 增大饱和度，土样吸力减小。图 3显示剪后吸力在第1阶段较初始吸力小，认为此时竖向应力增加土样饱和度对吸力影响比增大干密度对吸力影响大； 剪后吸力在第3阶段较初始吸力大，此时认为竖向应力增大干密度对吸力影响比增大饱和度对吸力影响大。图 4绘制了测试前后土体积含水量的变化，图 5绘制了剪后干密度随初始含水率变化。由图 4和图 5可知，含水率低于进气值对应含水率时，固结排水作用与压缩作用对试样体积含水率的改变甚微，而增大了干密度。荷载引起干密度的变化，对吸力的影响不仅与饱和度有关，还可能与土样结构性有关。在高含水率情况下，剪后含水率低于初始含水率，干密度显著大于初始干密度，含水率减少和干密度增大，都将增大吸力。

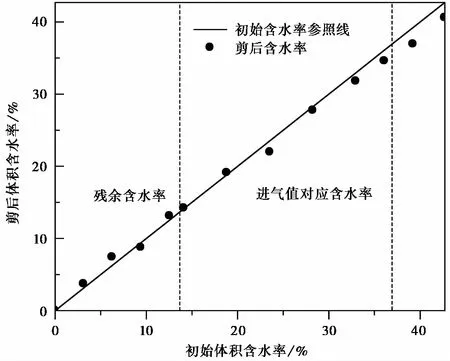
图 4 剪后体积含水率与初始体积含水率关系Fig. 4 Relationship between volumetric moisture content after shearing and initial volumetric moisture content

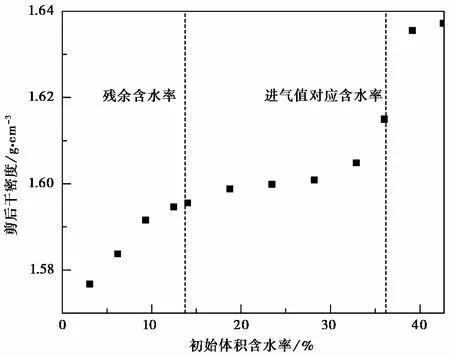
图 5 剪后干密度与初始体积含水率关系Fig. 5 Relationship between dry density after shearing and initial volumetric moisture content

土体含水率大于进气值所对应的含水率，固结和剪切导致土体排水，剪后含水率略小于初始含水率，当土体含水率小于进气值所对应的含水率，固结和剪切对土体的体积含水率没有影响。剪后干密度随着初始含水率增加而增加，呈反“S”型曲线关系。由图 5可知，初始含水率小于残余含水率时，压后干密度随初始干密度增加而增加，增速较快； 含水率介于残余含水率与进气值对应含水率之间，压后干密度随含水率增长缓慢； 初始含水率大于进气值对应含水率时，压后干密度随含水率增长速率加快。曲线形状与土-水特征曲线形状类似，拐点对应的含水率与土-水特征拐点对应的含水率接近，不同含水率土样对荷载的响应会在残余含水率和进气值对应的含水率处分异明显。

3 抗剪强度测试结果分析

常规直剪试验得到抗剪强度与含水率关系如图 6所示。随着含水率的减小，抗剪强度增大，当小于残余含水率时，抗剪强度骤增，残余含水率是影响抗剪强度的界限值。图 7所示为非饱和直剪强度和常规直剪强度与剪后吸力的关系，在同一吸力情况下，非饱和直剪的抗剪强度接近饱和段略低于常规直剪试验强度，含水率减小后又略大于常规直剪试验强度，但两种方法测得的强度变化趋势较为一致。

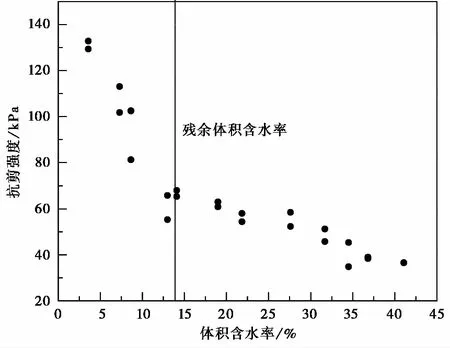
图 6 抗剪强度与体积含水率关系Fig. 6 Relationship between shear strength and volumetric moisture content

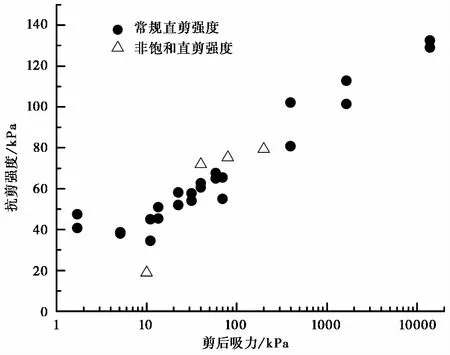
图 7 非饱和直剪强度与常规直剪强度与剪后吸力的关系Fig. 7 Relationship between unsaturated direct shear strength and conventional direct shear strength and suction after shearing

Vanapalli et al. (1996)基于加拿大的冰碛土，提出了式(3)的抗剪强度预测模型。

τf=c′+(σ-ua)tan(φ′)+(ua-uw)Θκtan(φ′)

(3)

式中，(σ-ua)为正应力(kPa)； (ua-uw)为剪切过程中的吸力(kPa)，假设剪切过程中吸力不变，则剪后吸力可代表剪切过程中的吸力；c′为有效黏聚力(kPa)；φ′为有效内摩擦角(°)；Θ为相对体积含水率，Θ=θw/θs；θw为体积含水率；θs为饱和体积含水率；κ为拟合参数。

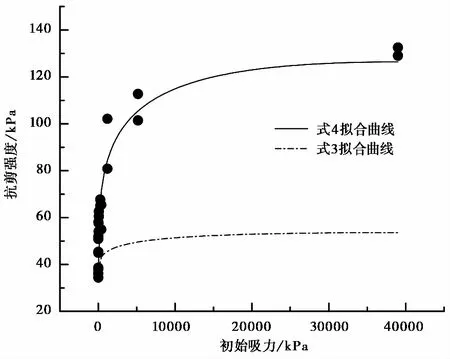
图 8 抗剪强度与初始吸力的拟合关系Fig. 8 The fitting relationship between shear strength and suction before shearing

图 8的虚线是采用式(3)对剪后吸力与抗剪强度测试点的拟合曲线，发现式(3)很大程度上低估了抗剪强度，直接用式(3)作为黄土的强度公式并不适合。式(3)是用含水率将吸力进行折减，一旦有效内摩擦角确定，折减率只与拟合参数κ有关。对于黄土，方程中Θκtan(φ′)计算的吸力折减率过大。本文结合公式(3)，对吸力折减相添加修正系数g，强度表达式如式(4)所示。

τf=c′+(σ-ua)tan(φ′)+

(ua-uw)(g·Θκ)tan(φ′)

(4)

式中，g为拟合参数。

上一节确定了初始吸力与剪后吸力的变化关系，即分为3段，在小于进气值和大于残余值部分，符合式(5)的近似关系，在两者之间，可认为定值。可将式(4)中剪后吸力转换为初始吸力，如式(6)所示。

(5)

(6)

式中， (σ-ua)为正应力(kPa)； 对于处于大气压下的常规直剪，ua=0；(ua-uw)为初始吸力(kPa)； (ua-uw)a为土-水特征曲线进气值(kPa)； (ua-uw)r为土-水特征曲线残余值(kPa)。

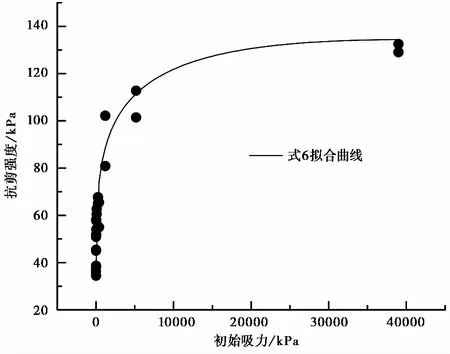
图 9 抗剪强度与初始吸力的拟合关系Fig. 9 The fitting relationship between shear strength and initial suction

由式(6)拟合抗剪强度和初始吸力测量值如图 9所示。得到拟合参数g=2.12，κ=2.25，拟合相关程度R2=0.95。可见式(6)能准确地描述黄土抗剪强度与吸力的关系。剪前吸力是目前用压力板仪或滤纸法较为容易测试的结果，而常规直剪被工程中广泛应用，式(6)避免了采用复杂耗时的非饱和强度测试过程，采用常规测试方法，就可以获得非饱和黄土的抗剪强度。

4 结 论

非饱和黄土剪切强度测试过程中，运用轴平移技术保持吸力不变得到非饱和抗剪强度，其试验操作复杂，周期漫长，为工程应用带来极大的不便。文献中提供的非饱和抗剪强度公式中，吸力多为剪切过程中的吸力，该数据在工程中难以获得。目前测量0压力的土样初始吸力技术较为成熟，积累大量的试验数据，成果丰硕。本文通过常规固快剪试验测试抗剪强度，并且用滤纸法测试了试样的初始吸力和剪后吸力，获得以下结论。

(1)详细探讨了饱和至干的土样完整吸力范围，固结与剪切对吸力的影响，通过初始状态和剪切后土样含水率与干密度的变化，分析了吸力变化的原因和趋势，发现土-水特征曲线的进气值和残余值对干密度和含水率的变化起控制作用。

(2)滤纸法测得的剪后吸力与常规直剪测得的抗剪强度，与非饱和控制吸力测得的结果具有较好的一致性。

(3)在Vanapalli非饱和土强度公式的基础上，提出了利用土样初始土-水特征曲线、有效黏聚力c′和有效内摩擦角φ′预测非饱和黄土抗剪强度的公式。研究成果为非饱和土抗剪强度理论在工程实践中推广应用提供了新思路。