水下输油管汇牺牲阳极阴极保护系统的优化

2020-05-23

腐蚀与防护 2020年4期

(1. 大连船舶重工集团设计研究院有限公司，大连 116001； 2. 大连理工大学船舶工程学院，大连 116024)

水下输油管汇作为海洋油气田开发中的关键设备，在水下油气开发中起到重要作用。由于其作业于海底，受恶劣环境影响较小，具有较强的可靠性，是经济、高效开发深海油田的关键基础设施之一。目前，水下管汇生产系统的设计一直被欧美少数国家所垄断。因此，面对我国未来水下油气田巨大的开发需求，开展水下管汇生产设备的研发已迫在眉睫[1-3]。

由于水下管汇生产系统永久系固于海底，且作业年限往往长达数十年，其间无法正常进行管汇的腐蚀维护。腐蚀问题可引发水下管汇结构失效，从而导致水下管汇系统不能正常工作，甚至引起油气泄漏事故，因此水下管汇腐蚀防护问题尤为重要。目前，牺牲阳极阴极保护方法以其简便性、经济性、可靠性、实用性等优点，广泛应用于水下输油管汇。但由于水下管汇系统较为复杂，其各个位置的牺牲阳极输出电流存在一定差异，在水下管汇寿命末期，某些输出电流较大的阳极可能会过早消耗完，从而导致阴极保护系统局部失效的情况发生，在设计阶段需对此问题进行考虑。

常用的阴极保护设计方法有经验法和数值模拟法。基于经验公式的设计方法[4]，可以根据被保护结构的水下湿表面积和相关环境参数给出设计结果，设计效率很高，但这种设计方法比较粗糙，无法考虑被保护结构的结构形式和牺牲阳极电流输出情况，容易造成某些输出电流较大的阳极过早消耗完，从而导致阴极保护系统局部失效。随着计算机性能和数值模拟方法的迅猛发展，数值模拟在阴极保护状态评估和设计中的应用日趋增加[5]，其方法包括有限差分法[6-7]、有限元法[8-10]和边界元法[11]。边界元法具有模型构建简单且易于处理无限域问题的优点，是目前用于阴极保护的主要数值模拟方法，已成功应用于埋地管道[12]，导管架平台[13]及海底管线[14]、船舶[15-16]等海洋工程结构阴极保护系统的设计和评估，但目前针对水下输油管汇阴极保护系统的数值模拟案例较少。为此，本工作将基于边界元法的数值模拟应用于水下管汇的阴极保护设计中。为了获得最佳的阴极保护设计方案，本工作先使用规范设计牺牲阳极尺寸并计算阳极数量，再通过数值模拟计算各牺牲阳极的输出电流，以各牺牲阳极的输出电流基本相同为优化目标，对牺牲阳极的布置进行优化，从而保证阴极保护系统在水下管汇全寿命周期内平稳有效。

1 原始模型

以作业于南海的某水下管汇牺牲阳极阴极保护系统为研究对象，其三维模型如图1所示。该系统依照DNV-RP-B401-2011《阴极保护设计》设计，同时结合南海环境条件[17-18]确定相关参数，如表1所示。该系统的牺牲阳极布置在海水中，阳极材料适合采用电容量较高的铝合金。依据规范设计的阳极尺寸和数量也列于表1中。

图1 水下管汇的三维模型Fig. 1 3D model of subsea manifold

2 模拟方法

基于规范的设计方法，仅能保证牺牲阳极总的电流量满足要求，无法预测水下管汇牺牲阳极实际状态。因此，本工作基于边界元法，开发了针对海洋工程结构物阴极保护的数值模拟软件，通过该软件对海底管汇各牺牲阳极的输出电流进行预测，并基于预测结果对牺牲阳极进行优化布置。

表1 南海某水下管汇阴极保护系统的参数Tab. 1 Parameters of cathodic protection system for subsea manifold in the South China sea

下面从控制方程、边界条件和相应的边界元法等方面对数值模拟的基本原理进行简要介绍。

2.1 控制方程

由电荷守恒可知，电位φ域内控制方程为Laplace方程[19]，如式(1)所示。

(1)

2.2 边界条件

边界条件为牺牲阳极和钢铁材料的极化曲线，如式(2)所示。

(2)

2.3 基于边界元的牺牲阳极阴极保护数值模拟

对于满足Laplace方程的阴极保护问题，其离散形式的边界积分方程如式(3)所示[20]。

(3)

式中：N=(N1,N2,L,Nn)为形函数；φ=(φ1,φ2,L,φn)T为边界节点处的电位；q=(q1,q2,L,qn)T为边界节点处的法向电流密度；ρ为海水电阻率；m为单元数；φi为第i个节点处的电位，φi*为三维Laplace方程基本解,见式(4)。

(4)

对每个节点进行积分，则可得线性方程组

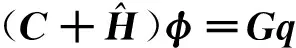
(5)

令

(6)

则方程(5)可以化成

Hφ=Gq

(7)

带入2.2节中的边界条件，将方程组变换成Aφ=b的形式，求解线性方程组，得到各节点处的保护电位。

3 模拟结果

基于DNV-RP-B401-2011规范的计算结果，牺牲阳极(共30块)布置如图2所示。

图2 水下管汇牺牲阳极初步布置方案Fig. 2 Initial arrangement of sacrificial anodes for subsea manifold

基于该水下管汇牺牲阳极布置的初步方案，建立的计算模型,并根据该初步方案进行数值模拟，得到水下管汇外表面阴极保护电位分布,如图3所示。通过对水下管汇牺牲阳极阴极保护系统的模拟计算，可得到各牺牲阳极的电流输出情况，具体如表2所示。

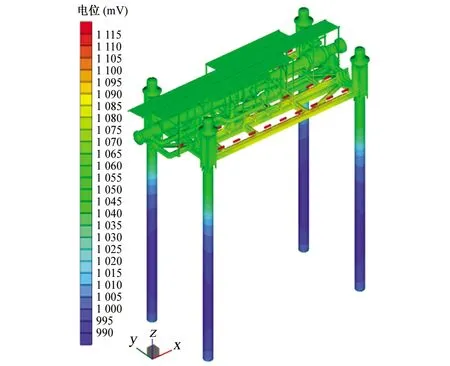
图3 基于初步布置方案模拟得到的水下管汇外表面的阴极保护电位Fig. 3 Simulated cathodic protection potentials on outer surface of subsea manifold based on initial arrangement

从表2可以看出，采用水下管汇牺牲阳极初始布置方案时，牺牲阳极输出电流的最小值为472.9 mA，最大值为728.9 mA，输出电流大小不均匀。该水下管汇须在海底持续工作25 a，在其寿命末期阶段，输出电流较大的牺牲阳极(如17号牺牲阳极)可能提前消耗完毕，从而导致阴极保护系统局部失效。

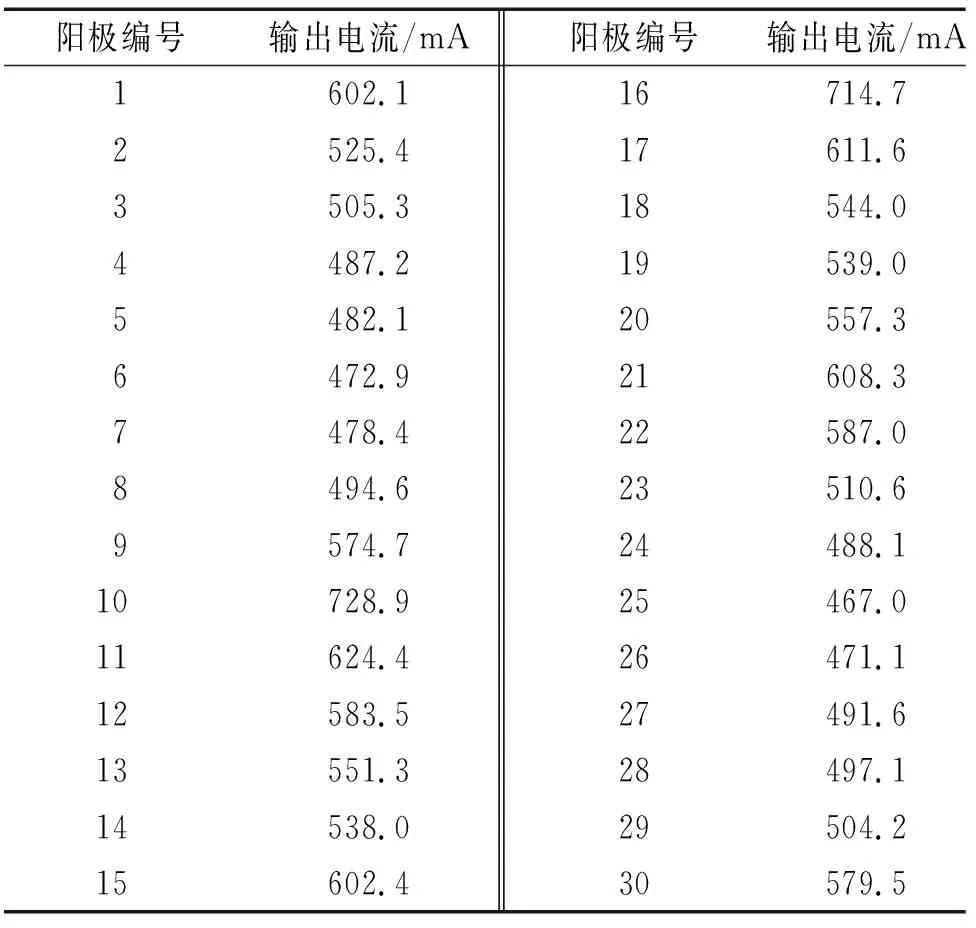
表2 牺牲阳极的输出电流(初步布置方案)Tab. 2 Output current of sacrificial anodes (initial arrangement)

为使各牺牲阳极的输出电流趋于一致，对计算结果进行进一步分析，对该水下管汇牺牲阳极的布置方案进行优化,如图4所示。根据优化布置方案建立水下管汇外表面保护电位的计算模型并进行数值模拟,模拟结果如图5所示。

图4 水下管汇牺牲阳极的优化布置方案Fig. 4 Optimized arrangement of sacrificial anodes for subsea manifold

由图5可知，优化牺牲阳极布置后，海水中涂装结构的阴极保护电位为894～1 125 mV，海泥中涂装结构的阴极保护电位为894～1 117 mV，海泥中裸钢结构的阴极保护电位为870～1 068 mV，整个水下管汇的阴极保护电位满足标准要求的800～1 150 mV，管汇的各结构均处于良好的保护状态。

图5 基于优化布置方案模拟得到的水下管汇外表面阴极保护电位Fig. 5 Simulated cathodic protection potentials on outer surface of subsea manifold based on optimized arrangement

优化牺牲阳极布置后，各牺牲阳极输出电流如表3所示。结果表明，优化牺牲阳极布置后，牺牲阳极的输出电流最小值为552.2 mA，最大值为581.4 mA。

对比优化牺牲阳极布置前后各牺牲阳极的输出电流情况，如图6所示。结果表明，优化后各牺牲阳极的输出电流基本趋于一致，较优化前有很大改善。但是，在牺牲阳极布置时，需考虑避开结构节点，而且阳极之间的距离至少应保持足够距离；另外，牺牲阳极布置后不能影响其他设备的安装、作业与维护等。受以上客观因素的影响，牺牲阳极不能随意布置，因此很难得到所有牺牲阳极输出电流完全一致的理想布置方案。