一种限制对比度的快速POSHE图像增强算法

陶佩，付青青，吴爱平 (长江大学电子信息学院，湖北 荆州 434023)

在实施成像过程中，自然光照环境、成像设备等因素会导致成像对比度过低，引起图像细节模糊，从而影响到工程人员对目标特征的分析评价[1]。直方图均衡(histogram equalization, HE)[2～4]是一种常见的图像对比度增强方法，因简单快速等特点而备受青睐。该方法通过将原始图像的灰度直方图从比较集中的某个灰度区间变成全部范围内的均匀分布，达到对比度增强的目的。传统的全局直方图均衡(gobal histogram equalization, GHE)利用图像的累积概率分布函数(cumulative distribution function, CDF)对整幅图像作单一映射, 拓展了直方图密集区域的对比度，从整体上提高了图像的对比度，但也压缩了直方图稀疏区域的对比度，造成部分背景细节丢失[5]。局部直方图均衡(local histogram equalization, LHE)[6，7]，则根据图像局部特性计算灰度变换函数来进行直方图均衡，对局部细节增强十分有效，但也容易造成过度增强。如子块重叠直方图均衡(BOHE)[3,6,8]，虽然能明显地提高局部图像对比度，但其同时也引起了严重的噪声和伪影痕迹。此外，该算法在执行时需要耗费过长的时间。Kim等[9]在提出的POSHE中通过增大移动步长加速了模板的移动过程，极大地提高了算法的运行效率，被广泛用于实时图像处理[10]。然而，它仍然无法避免过度增强效应。

Pizer等[11]率先提出了一种自适应限定对比度直方图均衡方法(CLAHE)来解决过度增强引发的噪声放大和图像畸变等问题。该方法根据像素转换后的灰度值与其CDF成正比的原则，通过对原始直方图进行阈值剪切来降低图像的CDF斜率，从而来限定对比度增强的程度，对增强水下图像和医学图像的质量效果显著。但这种单一的对比度限制方法在抑制噪声的同时也阻碍了图像细节的增强。为此，笔者提出了一种限制对比度的快速POSHE图像增强算法(简称快速POSHE算法)：通过对传统POSHE算法中子块直方图的创建方式与模板的移动路径进行改进，进一步提高实时图像处理的效率；再将对比度限制的方法引入到快速POSHE算法中，对每个子块先进行限制对比度剪切处理，而后执行快速POSHE算法。该算法在削弱过度增强时可显示图像隐藏的细节信息，使图像更加真实自然。

1 POSHE算法

在GHE中,图像的灰度转换函数T(r)表示如下[12,13]：

(1)

(2)

式中:p(r)表示输入图像灰度级为r的概率密度；nr是灰度级r上的像素总数；n是图像的像素总数；L是总的灰度级数。

式(1)右边为图像的CDF，这种灰度映射的过程称之为直方图均衡。POSHE算法是在图像的小区域里进行直方图均衡操作。通过一个模板来规定子区域的范围(见图1)，模板尺寸为3×3，其覆盖的第1个子区域包含的像素为a，b，c，d，e，f，g，h和i。假定模板的移动步长为2，算法的具体执行过程如下[9]：①模板每次向右移动一个步长至下一个子区域(如第2个子区域包含像素c，f，i，j，k，l，o，p，q)，并对其每次覆盖的子区域作直方图均衡处理；②重复执行①操作直至模板移动到该行最右边；③ 当每行遍历完后向下移动一个步长并转至该行左边，进行②操作，直至模板遍历完整个图像；④累计每个像素每次直方图均衡后的灰度值，其累计值与累计频率的模即为最终得到的输出值。

POSHE算法让每个像素依据自身邻域的CDF来进行灰度转换，弥补了GHE难以适应图像局部特性的缺陷，显著地提高了图像的局部对比度。然而，这种均衡效果也极容易造成过度增强，导致处理后的图像产生严重的噪声。

2 快速POSHE算法

鉴于在POSHE算法的执行过程中相邻子块间存在大面积的区域被重复直方图均衡化，笔者参考文献[14]中改进BOHE算法提出了一种快速POSHE算法，通过减小子块间部分区域不必要的重复操作，降低算法复杂度，从而提高运行效率。

2.1 改进子区域直方图的创建方式

在模板的移动过程中，相邻2子块直方图之间的关系如式(3)所示：

(3)

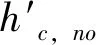
2.2 改进模板的移动方式

改进的模板移动方式如图2所示。模板的大小为3×3，移动步长为2，当模板移动到第1行的右端时，向下移动1个步长到该行右端，然后再从右边移动到左边，依次循环。这种形如蛇状的路线解决了上一行与下一行的前后子区域互不关联的问题，使模板在纵向移动时也可以使用快速子直方图的创建方式。结合这2种改进，只需要以整幅图像的第1个子区域的直方图为基准，其余的子区域在创建直方图时都只需要更新与前一个模板覆盖区域不重叠部分的直方图。由此可知，改进的模板移动方式进一步减小了子直方图生成时需要统计的像素数量。

为了验证快速POSHE算法的性能，将其与传统POSHE算法进行仿真测试并比较算法的时间与效果。设置模板为128×128，移动步长为16。通过计算增强图像之间的均方误差 (mean square error, MSE)可以直观地比较2种算法的增强结果是否一致。式(4)为MSE的定义:

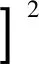
(4)

式中：εmse为均方误差，1;g1和g2表示传统与快速POSHE算法增强的图像；M×N表示图像的尺寸。

在MATLAB中测试众多不同尺寸的图像以得到更精确的时间比较结果，选取部分结果进行展示。图3显示了传统和快速POSHE算法仿真的图像结果，表1记录了增强图像测试的时间与εmse。记录的时间均为同一条件下反复测试的结果。仿真表明， 随着图像尺寸的增大，时间减少的速率也越来越大；同时，εmse表明了快速POSHE算法与传统POSHE算法对图像的增强效果一致。

表1 增强图像的测试时间与MSE结果

3 限定对比度

CLAHE[11]是一种削弱过度增强的重要技术。像素经直方图均衡转换后的灰度值正比于其CDF，对式(1)左右两边求导[16]：

(5)

式(5)左边为CDF斜率，右边是r的概率密度，由此可以得出结论：图像的对比度增强程度与其概率密度成正比。因此，限定对比度主要是通过设定每个灰度级的密度上限阈值，以实现图像CDF斜率的减小，从而控制对比度增强。当一个灰度级上拥有的像素数目超过设定的阈值时，多余的数目将被剪切，并分配给其余不足的灰度级上。图4显示了直方图的剪切与重分配的结果,图4(b)中蓝色曲线表示原直方图，阴影部分的“1”和“2”表示灰度数目超过阈值的区域，它们被分配到阴影部分的“3”，“4”，“5”区域，形成剪切后的直方图曲线，即图4(b)中黑色曲线所示；图4(c)中的蓝色与黑色曲线则分别表示图像剪切前后的CDF，由此可知，直方图剪切技术使CDF在原来陡峭的地方变平缓，故其对比度增强程度会减小，过度增强也得以削弱；图4(d)中矩形标记区域出现的大量斑点噪声在图4(e)中得到了抑制；图4(d)呈现出一种不自然的视觉效果，而图4(e)则更符合人的视觉感受，究其原因，对比度过度拉伸使增强的结果偏离真实；相比之下，图4(e)增强的细节更加细腻清晰。

将限定对比度引入到快速POSHE算法，以解决过度增强引发的噪声等问题。根据POSHE算法特性，像素的灰度转换函数是由局部子块的CDF决定的。因此，在各个子块被快速POSHE算法处理前，先进行限定对比度的直方图剪切与重分配，具体步骤如下[17]：

1)定义原图像为M×N，使用的模板为m×n。计算子块中每个灰度级的平均像素数目α，即:

(6)

根据α设置合适的灰度级上限阈值β。

2)定义Excess为子块中超出的阈值总数，其计算方式为Excess=Excess+h(n) -β, 其中h(n) (n=0, 1, 2, …,L-1)为每个灰度级上的像素数量。

(1) 当h(n) >β，令Excess=Excess,h(n) =β。

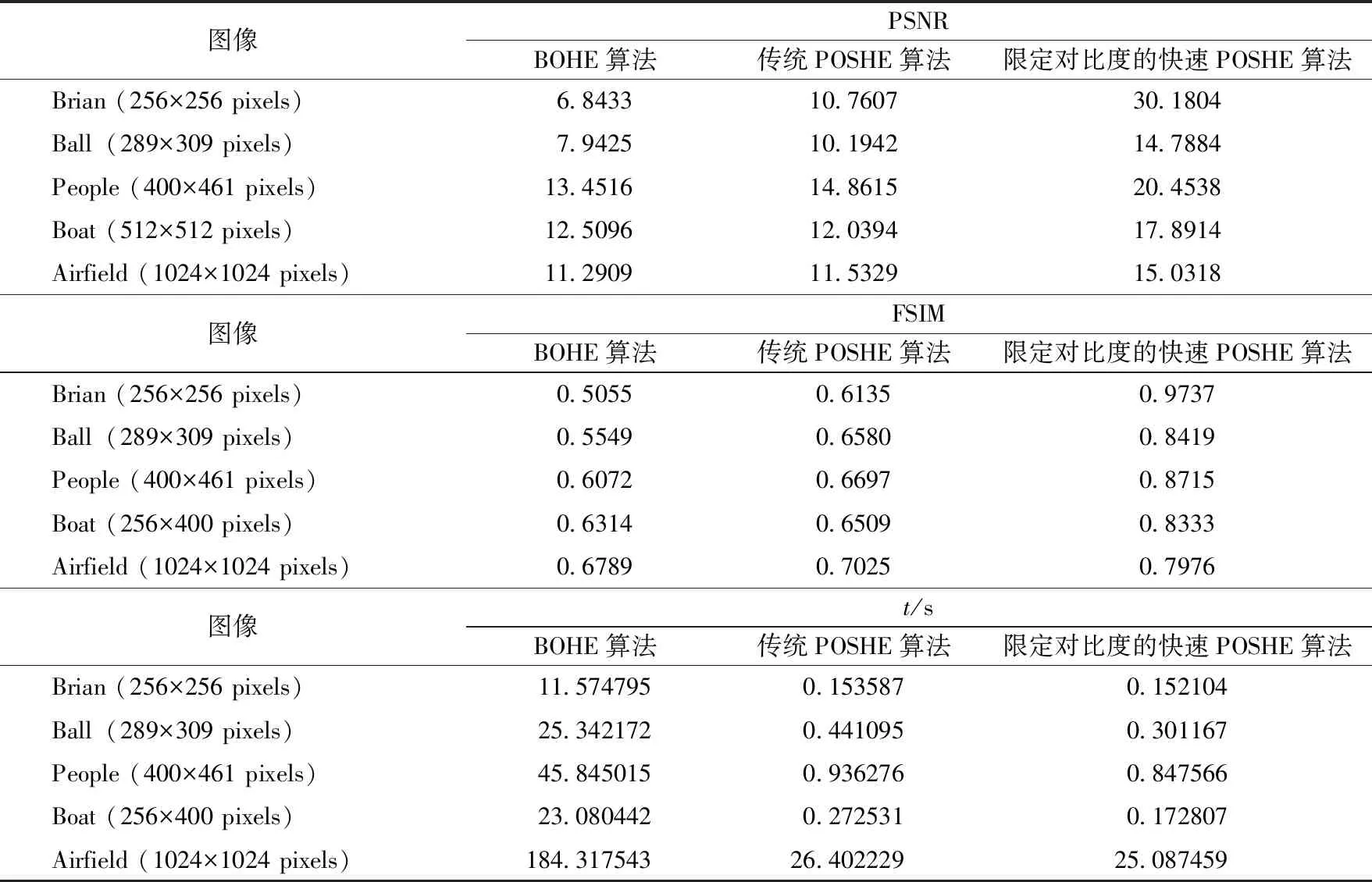
(2) 当β-q

(3) 当h(n) <β-q, 令Excess=Excess-q,h(n) =h(n) +q。

4)如果此时还有超出的像素数没有被分配完，将剩余的数目均匀地分布到像素数目不足阈值的灰度上，即：

当Excess> 0 且h(n) <β时， 令h(n) =h(n)+1，Excess=Excess-1，直到Excess= 0。

对比度限定的效果依赖于β的选取[18]，β越大，则对比度增强的程度就限制得越小；反之限制得越大。显然，β一定大于α。但是，过多的限制对比度增强不利于图像细节的显示。最佳方法是结合图像中存在噪声级别的先验知识来自适应选择β。通常，使用的模板越小，POSHE算法产生的过度增强越严重，噪声随之增多。因此，阈值的设定应当是随着子块的减小而减小。

4 试验结果及分析

4.1 主观评价

图5展示了限定对比度的快速POSHE算法以及BOHE算法和传统POSHE算法仿真结果。图5(a)中，原图像Brain背景区域的灰度较低，局部图像的灰度受噪声点的影响极易被过度提高，因此，BOHE算法和传统POSHE算法均产生严重的噪声，同时，图中目标区域的对比度较大，较暗区域的灰度也易被过度增强，导致BOHE算法和传统POSHE算法目标物的内部结构反而更模糊；经过了限定对比度处理之后，限定对比度的快速POSHE算法有效地克制了噪声的增加，也展示出大脑内部更多的细节信息。图5(b)中，BOHE算法虽然极大地提高了原图像Ball的亮度，但依然引起大量的斑点噪声和球面不自然的反光现象；传统POSHE算法甚至还产生轻微的块效应；限定对比度的快速POSHE算法则比较适度地提高了对比度，揭示的局部细节更加自然。 图5(c)中，由于雾霾造成了原始图像People对比度过低，致使图像不清晰；BOHE算法和传统POSHE算法通过增加对比度明显地提高了图像的可见度，但人脸、地面和上空区域却发生一定程度的畸变，过度增强是产生畸变的首要原因；限定对比度的快速POSHE算法增强的图像中不存在这些畸变现象，并呈现出一种良好的去雾结果。图5(d)中原图像Boat中发生过度增强最明显的地方在于云层。图5(f)中,对于原图像Airfield，大量的噪声和过饱和的伪影破坏了BOHE算法和传统POSHE算法图像中的细节，导致图像质量更差；而限定对比度的快速POSHE算法增强的对比度更适合显示图像细节。

4.2 客观评价

通过计算增强图像的峰值信噪比(简称PSNR)[15]和特征相似度指数(简称FSIM)[19]来评价限定对比度的快速POSHE算法性能:

(7)

(8)

式中:Rpsn为峰值信噪比，1;Ifsm为图像特征相似度指数，1；Ω表示图像的空间域；x和y分别为原始图像和增强的图像；PC表示图像的相位一致性信息，PCm(x,y)=max(PC(x)，PC(y))；SPC(x,y)和SG(x,y)是x和y的相位相似值和梯度相似度值[20，21]：

(9)

(10)

式中：T1为一个防止分母为0的常量，其值一般设置为0.0001；T2的作用和T1一样。

通常，FSIM模型用来衡量增强图像与原始图像的失真度，取值范围为[0，1]。FSIM值越大，增强图像的失真度越小，质量就越高。

表2记录了图4中增强图像的PSNR和FSIM以及各算法的运行时间。从表2中可以看出，每一幅图像由限定对比度的快速POSHE算法得到的PSNR和FSIM均大于前2种算法中的值，客观地表明了限定对比度的快速POSHE算法更有利于保持图像真实度。结合主观视觉感受，印证了限定对比度的快速POSHE算法在通过提高对比度来增强图像细节时有效地避免了过度增强。

同时，表2也显示了限定对比度的快速POSHE算法的运行时间最少，进一步证明了该算法具有极高的性能。

表2 PSNR, FSIM和算法运行时间t的比较

5 结语

笔者提出了一种限制对比度的快速POSHE算法，该算法通过对POSHE中局部直方图的创建方式以及模板的移动方向进行改进，极大地降低了算法的复杂度。仿真试验表明，该算法在处理大尺寸图像时能明显提高算法的效率。此外，将限定对比度方法引入至快速POSHE，通过控制子块的对比度增强程度能有效地抑制噪声的产生。主观与客观的评价均表明，该算法不仅可以显示隐藏的图像细节，还较好地保持了图像的真实度。