基于粒子群优化算法的三维无线传感器网络覆盖增强方法
2020-05-23张磊焦正华长江大学电子信息学院湖北荆州434023
张磊,焦正华 (长江大学电子信息学院,湖北 荆州 434023)
许淼 (长江大学档案馆,湖北 荆州 434023)
李兴五,李鹏,郭颂,王思诚 (长江大学电子信息学院,湖北 荆州 434023)
目前,对于无线多媒体传感器网络(wireless multimedia sensor networks, WMSNs)的覆盖增强研究大多集中在二维平面[1~4],由于没有考虑感知高度信息,这些模型不能描绘真实的三维物理环境,为此研究者设计出更为准确的三维有向感知模型。如Ma等[5]提出基于水平感知和垂直感知的三维有向感知模型,肖甫等[6]在文献[5]基础上,提出俯仰角优化和偏向角优化的覆盖增强策略,但都未考虑节点的感知范围。同时,现有文献[7~11]大多通过调节节点的主感知方向来实现对监测区域的最优覆盖。
Latif等[12]针对水下无线传感网络的能耗问题,提出冗余覆盖策略和覆盖盲区修改策略来有效减少能耗;杨永建等[13]提出一种探索能力增强型的粒子群算法,并利用该算法优化概率覆盖模型以提高覆盖率;Qasim等[14]通过改进标准蚁群算法,提出一种基于改进蚁群算法的部署方法;孙泽宇等[15]提出基于概率模型的优化覆盖方法,有效改善了覆盖率和生存周期;Sun等[16]提出一种基于复杂联盟策略的多目标覆盖增强方法,从而实现能耗和覆盖率的优化;Xu等[17]提出一种混合多目标分解优化算法,并融合离散二进制粒子群策略,来优化覆盖率和生存周期。上述方法均通过随机方式部署节点,导致大量节点集中,节点间会存在很多感知重叠区域,此时不管如何调节节点的主感知方向,监测区域的覆盖率均不会有明显的提升,致使覆盖增强方法的收敛性不高。为此,笔者加入节点感知高度信息和节点感知半径,设计了一种更符合三维物理环境的三维锥体有向感知模型。同时,推导得出单个节点的最佳投影面积及其对应的俯仰角,并在此基础上利用粒子群优化算法来调整节点的位置信息,从而实现对监测区域的最优覆盖。
1 三维锥体有向感知模型
笔者设计的三维锥体有向感知模型如图1所示。根据参考文献[18]得出,该三维锥体有向模型在二维平面的投影是椭圆ACBD。图中,P为传感器节点,节点的高度为h,节点感知半径为R;AB是椭圆的长轴,CD是椭圆的短轴,H是AB和CD的中点,即椭圆的中心;PK垂直椭圆ACBD;PG是∠APB的角平分线;∠KPG=γ为传感器垂直方向上偏移的角度,即仰俯角;∠APB=2β是传感器垂直方向感知区域视角;水平方向感知区域视角为2π。
2 无线多媒体传感器网络的覆盖优化
为实现WMSNs的最优覆盖,一方面可以优化单个节点的俯仰角,使其投影覆盖面积最大;另一方面可以调整所有节点的位置,减少节点间的感知重叠区以改善覆盖率。同时优化会导致复杂度过高,通过进一步分析发现,单个节点的二维投影面积只与仰俯角有关,所以可以先求解节点的最优仰俯角,再优化节点的位置信息,减少感知重叠区和感知盲区,进而提升覆盖率。为此,笔者将覆盖增强过程分为基于仰俯角的节点投影覆盖面积优化和基于粒子群算法的位置信息优化。
2.1 基于仰俯角的节点投影覆盖面积优化
如图2所示,P为节点,圆锥PMWNV为P的空间感知区域;椭圆ACBD为节点在二维平面的投影,PN为P的最大感知半径,即PN=R;∠APB=2β,即为P的垂直感知区域视角;PG为∠APB的角平分线,则PG必定在圆锥PMWNV的中心轴PQ上;∠KPG=γ,即传感器的俯仰角;节点P高度为h,即PK=h。设∠GPH=θ,过椭圆ACBD的中心点H作垂直中心轴PQ的圆ECFD,圆心为O,与PN、PM分别相交于点E、F。
下面推导单个节点的二维投影面积及其对应的最优俯仰角,具体如下。
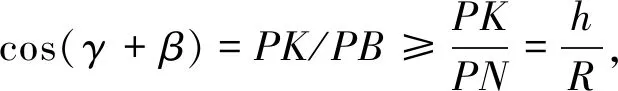
又AK=PK×tan(β-γ)=htan(β-γ),BK=PK×tan(β+γ)=htan(β+γ),所以椭圆ACBD的长半轴a为:
故:
又PK垂直于椭圆ABCD, 所以PK⊥KH,则:
由OH⊥PQ,且O,H,C,D,E,F在同一个面上, 所以EDFC必定是一个圆,又PD=PF,则圆EDFC和圆MWNV相互平行。
在∆OPH中,∠OPH=∠GPH=θ,PO=PHcosθ,从而有PD=PF=PO/cosβ=PHcosθ/cosβ。
又CD⊥面PKH, 所以PH⊥CD,则椭圆ACBD的短半轴b为:
2018年是ABB持续投资中国、优化业务布局的一年。例如,ABB在重庆设立的机器人应用中心正式开业,以重点满足西部地区汽车、3C产品制造、装备制造和消费品制造等领域对工业机器人快速增长的市场需求;不久前,ABB宣布将投资1.5亿美元,在上海康桥建设其全球最大、最先进的机器人超级工厂,以扩大产能,提升效率,巩固领先的市场地位,更好地满足激增的客户需求;而投资额约3亿美元的ABB厦门工业中心将分散于厦门岛内的多家企业合而为一,全面提升ABB自身的生产效率和核心竞争力。
b=HD
所以椭圆ABCD的面积为:
S=π×a×b
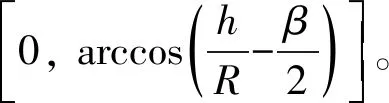
2.2 基于粒子群优化算法的位置信息优化
在得出最优仰俯角γ后,单个节点的覆盖面积将达到最大。但由于通过随机方式部署大量节点,会造成节点间存在着很多感知重叠区,所以需要优化节点位置以降低感知重叠区,进一步提升覆盖率。为此,引入收敛速度快、搜索效率高的粒子群算法[19,20]来调整节点位置。
设在监测区域内随机部署n个节点,则这组节点的初始位置可表示为(s1,…,sj,…,sn),其中,sj为(x,y),代表节点j在二维平面X-Y上的坐标。设种群中粒子规模为m,则粒子xi的位置为(xi,1,…,xi,j,…,xi,n),i=1,…,m,j=1,…,n,sj=xi,j。粒子xi的速度为vi=(vi,1,…,vi,j,…,vi,n),定义粒子xi的适应度函数为fi:
fi=f(xi,1,…,xi,j,…,xi,n)
(1)
式中:fi的值代表覆盖率。
粒子的速度和位置更新分别如式(2)和式(3)所示。
(2)
(3)
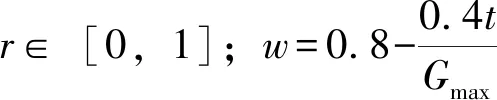
为保证种群粒子始终在可行域内进行搜索,当vi,j超出可行域范围时,则调整为:
vi,j=r×(vmax-vmin)+vmin
当xi,j(t)超出可行域范围时,则调整为:
xi,j=r×(xmax-xmin)+xmin
式中:vmax和vmin分别为粒子最大和最小速度;xmax和xmin分别为粒子的最大和最小边界范围。实质上,粒子的初始位置和初始速度也是根据上述方法生成的。
综上,采用粒子群算法优化节点位置的具体步骤如下:
Step 1设置初始参数。节点数量m,种群规模n,最大进化代数Ngmax,学习因子C1、C2,w为动态权重。生成初始种群,包括每个粒子的位置和速度。
Step 2计算粒子的适应度值,即每个粒子所代表的覆盖率。
Step 3根据式(2)和式(3)更新粒子的位置和速度。
Step 4判断是否达到最大进化代数,是则结束,并输出最优粒子的位置,即为传感器网络中节点的部署;否则返回Step 2。
3 仿真试验
为保证对比的公平性,所有算法中涉及相同的参数均取值一样。参考文献[6],试验参数设置如下:在200m×200m的二维监测区域内,随机布撒若干节点,每个节点高度h=6m,节点感知半径R=30m,节点水平感知视角为2π,垂直感知视角β=2π/3。最大进化代数Gmax=100,种群规模n=100,学习因子C1=C2=1.5,vmin=-10,vmax=10,计算出节点的最优俯仰角18.46°。所有试验均在硬件配置为Intel(R) Core(TM) i7-7500U CPU@2.70GHz的计算机上进行,采用MATLAB2014编程。试验中节点数量m=40、50、60、80,仿真试验结果如图3~6和表1、表2所示。
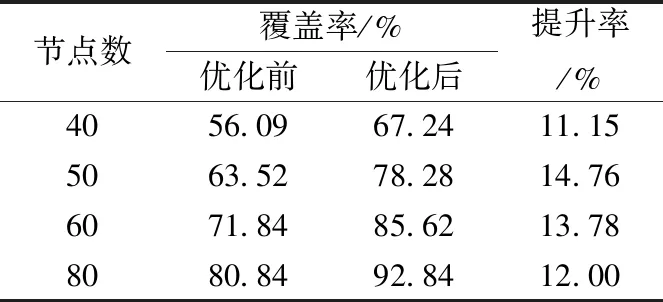
表1 不同节点数量时的覆盖率
从图3~6可以看出,当节点的俯仰角为最优俯仰角时,节点在二维平面的投影形状和面积均一样。未对节点位置进行优化前,由于是随机部署所有节点,节点的分布不均匀,而且节点间存在大量的感知重叠区和感知盲区;对节点的位置进行优化后,节点分布更加均匀,节点间的感知重叠区和感知盲区明显降低,整个网络的覆盖率得到较大程度的提升,这表明节点位置优化的有效性和必要性。同时还可以看出,随着节点数的增加,监测区域基本得到较好的覆盖,但节点之间的覆盖重叠区也随之增加。

表2 不同算法覆盖率
从表1可以看出,当节点较少时,覆盖率的改善不太明显。这是由于此时节点间的覆盖重叠区较少,通过优化节点位置来提升覆盖率的效果不太大。随着节点数的增多,未优化前的覆盖率随之提高,但此时节点间的覆盖重叠区也增多,通过节点位置优化后,覆盖率得到较大程度的提升。
从表2可以看出,在相同的初始覆盖率情况下,笔者的算法通过优化俯仰角和节点位置优化,最终取得了更优的网络覆盖率,具备一定的优势。这进一步说明了笔者提出的基于俯仰角优化和节点位置优化的粒子群覆盖增强方法可以有效减少覆盖重叠区和感知盲区。
4 结语
笔者对现有感知模型和覆盖增强方法存在的问题展开了研究,一方面引入感知高度信息和节点感知半径,设计出一种三维锥体有向感知模型,并推导出最优二维投影面积;另一方面采用粒子群算法优化节点的位置信息,以提升覆盖率。仿真试验结果表明了该方法较好地提升了覆盖率。下一步的研究工作将围绕节点冗余问题展开研究,即以最少的节点数和能耗最大化网络覆盖率。
