基于改进PSO算法优化GRNN的煤与瓦斯突出预测
2020-05-23胡业林占晨阳郑晓亮宋晓安徽理工大学电气与信息工程学院安徽淮南232001
胡业林,占晨阳,郑晓亮,宋晓 (安徽理工大学电气与信息工程学院,安徽 淮南 232001)
煤与瓦斯突出是指煤体中大量的煤与岩石被抛出并喷出大量瓦斯的动力现象,其影响因素众多,如地应力、瓦斯等。煤与瓦斯突出对煤矿安全生产意义重大,较高准确度的煤与瓦斯突出预测是安全生产的必要前提和保证。煤与瓦斯突出事故是煤矿重大灾害之一,具有极大的危害性。煤矿为了进一步提高生产能力,需要不断增加开采深度,扩大开采规模,煤层压力和瓦斯含量则随深度的增加而增加,突出的危险性也愈发严重。因此,准确地预测煤与瓦斯突出对煤矿的安全生产有很重要的实际意义。
煤与瓦斯突出的作用机理非常复杂,影响因素众多,使用单一指标方法难以囊括所有的影响因素,所以多指标预测[1~4]成为煤与瓦斯突出预测的关键环节。煤与瓦斯突出区域预测一般根据煤层瓦斯参数结合瓦斯地质分析的方法进行。传统方法通过建立数学模型,选择合理的指标对煤与瓦斯突出进行预测,但数学模型很难准确反映出煤与瓦斯突出之间的复杂映射关系。神经网络方法是一种基于人工智能的非线性预测方法,具有很强地并行运算能力和自学习能力,目前在煤与瓦斯突出预测中已被广泛运用。曲方等[5]开发了基于BP神经网络的煤与瓦斯突出预测系统;郝天轩等[6]使用模糊神经网络对煤层瓦斯含量预测进行了研究;师旭超等[7]以径向基函数为核函数建立了煤与瓦斯突出SVM预测模型。这些预测模型的预测效果一般,存在着自己的局限性。BP神经网络学习效率不高,容易出现局部极小的问题,影响其实际应用;模糊神经网络受输入变量和训练次数的影响较大,容易出现欠拟合或过拟合,影响其预测精度;SVM模型需要繁琐的参数优化选择,模型预测效率不高。广义回归神经网络(GRNN)具有很强的非线性映射能力和分类能力,学习速度快,相较于标准的前馈神经网络有更好的全局收敛性,十分适合煤与瓦斯突出预测。付小平等[8]使用GRNN模型对煤与瓦斯突出及瓦斯含量进行预测,并提出合理的选取GRNN的光滑因子对预测精度十分重要。笔者利用寻优算法对模型参数进行优化,解决了参数选取的问题。基于果蝇优化算法(FOA)[9]和粒子群优化(PSO)算法[10]优化的煤与瓦斯突出预测虽然有一定效果,但是在准确度和泛化能力上有所欠缺。改进PSO算法具有参数少,计算简单,寻优精度高等优点,且避免了PSO算法原本易于陷入局部最优的问题。改进PSO算法优化GRNN可以找出全局最优光滑因子,从而最大限度的提高了神经网络模型的预测能力。
1 煤与瓦斯突出预测影响因素的选取
煤与瓦斯突出影响因素包括瓦斯含量、瓦斯压力、瓦斯放散初速度、煤层坚固性系数、孔隙率、开采深度、软分层厚度、煤层透气性以及煤层地质构造等。在煤与瓦斯突出智能预测中,将各种影响因素作为模型输入时,选取合适的输入尤为重要。通过查阅相关文献[11~15]后研究发现,实际预测中选取过多的影响因素会使工作量增多,不利于准确预测。由于各种影响因素之间有着复杂的耦合关系,通过降维的方法[16]可以从中选出核心的影响因素。将核心影响因素作为神经网络模型的输入不仅可以提高煤与瓦斯突出预测的准确度,还能提高预测的效率。
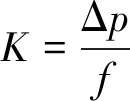
2 煤与瓦斯突出结果分类
在煤与瓦斯突出预测中,不仅结果的准确性至关重要,结果的分类也同样重要。从过往对煤与瓦斯突出预测的研究中发现,大多数人会将突出结果分为4类,分别为不突出、小型突出、中型突出和大型突出。煤矿企业在实际的生产中,通过对煤与瓦斯突出预测后,对于预测不突出的情况,可继续按照既定生产计划进行生产;对于预测为突出的情况,无论突出大小都需要采取消突措施保障煤矿开采的安全。针对这种情况,笔者在进行预测时,将结果分为突出和不突出2类,更符合煤矿安全生产实际。
3 GRNN原理
GRNN是建立在数理统计基础上的径向基函数网络,其理论基础是非线性回归分析。GRNN具有很强的分类能力和较快的学习速度,并且网络的学习对样本的依赖程度高,非常适合应用于煤与瓦斯突出预测。
GRNN在结构上由4层构成,分别为输入层、模式层、求和层和输出层,如图1所示。
输入层神经元的数目等于学习样本中输入向量的维数,各神经元是简单的分布单元,直接将输入变量传递给模式层。
模式层神经元数目等于学习样本的数目n,各神经元对应不同的样本。模式层的传递函数为径向基函数,通常采用高斯函数作为网络的传递函数:
(1)
式中:σi为光滑因子(光滑因子越大,则基函数越平稳);Ri(x)为第i个神经元的输出;c为高斯函数的中心值; ‖x-c‖为输入x到中心值c的模长。
求和层中使分母神经元和分子神经元进行求和,分母神经元对模式层中所有神经元的输出进行算数求和,所有连接的权值均为1。分母神经元的传递函数为:
(2)
式中:SD为分母神经元函数;pi为模式层的输出。分子神经元对模式层中所有神经元输出加权求和,求和层第i个神经元与模式层第j个神经元之间的连接权值为yij,即第i个输入样本的第j个元素。分子神经元的传递函数为:
(3)
式中:SNj为分子神经元传递函数。输出层中的神经元数目等于学习样本中输出向量的维数k,各神经元将求和层的输出相除,算出yi的估算值:
(4)
式中:yi为模式层的输出。
4 改进PSO算法
4.1 PSO算法
PSO算法模拟鸟群的捕食行为并从中得到启示来解决优化问题。PSO算法中,每个优化问题的解都是搜索空间中的一只鸟,称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitness value),每个粒子都有一个特定的速度决定了飞翔的方向和距离。所有粒子根据当前的最优粒子在解空间中搜索。PSO算法参数少,搜索速度快,易于工程实现,但容易陷入局部最优,对参数的选择较为敏感。
PSO算法初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪2个“极值”来更新自己。一个就是粒子自身历史最优解,叫做个体极值。另一个是整个种群目前找到的最优解,叫做全局极值。
在找到这2个最优值时,粒子根据式(5)和式(6)来更新自己的速度和位置:
(5)
(6)
4.2 自适应惯性权重
在PSO算法的速度更新公式中,惯性权重w是算法的重要改进参数, 通过设置w可以改变上一代粒子位置对当前位置的影响。较大的w可以加快粒子搜索速度,提高全局搜索能力,而较小的w会降低粒子搜索速度,提高局部搜索能力。由于粒子在搜索的每一代都可能获得最优值,而传统的线性微分递减策略只是根据代数对w进行调整,并不能有效地平衡算法的全局与局部搜索能力。为了解决上述问题,采用(0,1)随机均匀分布策略[19], 可以在迭代初期和后期均可得到较大的值,提高全局搜索效果。w的更新公式为:
w=0.6+0.6×rand()
(7)
w=0.8×rand()
(8)
式(7)为当代个体极值等于全局极值时w的更新公式,否则利用式(8)进行更新。
4.3 线性调整学习因子
PSO算法中的自身学习因子c1和社会学习因子c2对搜索能力也有一定的影响。搜索初期c1取值较大,c2取值较小,增加认知的比重,可以提高全局搜索能力。搜索后期c1取值较小,c2取值较大,增加社会学习因子c2的比重,可以提高局部搜索能力。
学习因子线性调整为:
(9)
(10)
式中:c1max=c2max=2;c1min=c2min=1 ;Ng为粒子代数;Ng,max为最大粒子代数。
5 基于改进PSO算法优化GRNN的具体情况
将数据分为训练样本和测试样本,训练样本用于训练模型,测试样本代入所建模型。基于改进PSO算法优化GRNN模型实现步骤如下:
步骤1归一化预处理样本集。
步骤2初始化改进PSO算法参数,生成初始位置和速度。
步骤3将测试数据集预测结果和实际结果的均方差作为适应度函数,适应度值越小优化结果越好,根据适应度值更新pbestid和gbestd。
步骤4更新惯性权重w和学习因子c1、c2。
步骤5更新粒子各个维度的速度和位置。
步骤6计算每个粒子适应度值,与全局最优适应度值进行比较,决定是否更新;判断是否达循环结束条件,达到退出循环,否则继续迭代。
步骤7利用优化所得参数对模型进行训练。
步骤8输入测试样本进行预测。
6 仿真与试验分析
试验在Matlab2017a上进行仿真。在模型预测中,训练样本和测试样本的数量对预测效果影响较大,过多的训练样本会导致过度学习,而过少的训练样本会使预测效果变差。笔者选取瓦斯含量、瓦斯压力、瓦斯放散初速度、煤层坚固性系数和孔隙率5个指标,以79个原始数据为训练样本,20个原始数据为测试样本。原始数据采自于淮南矿区,选取部分有代表性的训练样本,如表1所示。
由于不同特征的物理意义不同,其取值范围也相差很大。当某些特征或分量的值过小,在计算过程就无法起到相应的作用;当取值过大,其作用又会过于明显。为了解决上述问题,将每一个特征分量进行归一化,使其分布在一个有限的值域里。笔者使所有特征向量归一化至[0,1]区间。
利用改进PSO算法对GRNN模型参数进行优化,利用得到的最优参数对煤与瓦斯突出结果进行分类。根据样本的数量和输入向量的维数,对改进粒子群优化算法中的初始参数进行设置。种群数量为10,粒子维数为2,初始惯性权重w=0.5,c1=c2=1.2,迭代次数设为100。
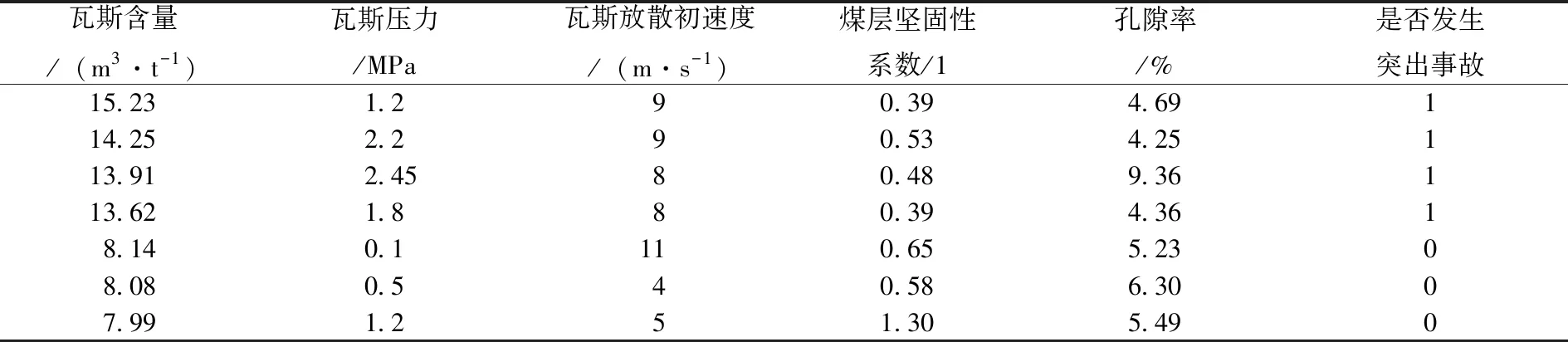
表1 部分训练样本
注:1代表实际发生了突出事故;0代表没有发生突出事故。

表2 各模型训练结果对比
分别用FOA、PSO算法和改进PSO算法优化的GRNN模型进行煤与瓦斯突出预测,每个算法进行10次预测,其结果如表2所示。
其中,FOA在10次预测中,最小方差和平均方差之间相差较大,表明FOA易陷入局部最优,无法稳定找到最佳参数。FOA的预测结果中第5个、第11个、第13个预测错误,对实际突出数据的预测准确率为75%,实际不突出数据的预测准确率为86.7%,总体预测准确率为85%。PSO算法在10次预测中,虽然最小方差和平均方差之间相差较小,表明PSO算法比FOA更适合该模型,但仍然有陷入局部最优的问题。PSO算法的预测结果中第11个、第13个预测错误,实际突出数据的预测准确率为100%,实际不突出数据的预测准确率为86.7%,总体预测准确率为90%。改进PSO在10次预测中,全部预测都找到了最佳光滑因子,解决了前2种算法易陷入局部最优的问题,算法稳定性更好。改进PSO算法的方差最小,表明改进PSO算法寻优效果最好,分类精度最高,泛化能力最强。
针对改进PSO算法的预测结果,将实际结果与预测结果对比,如表3所示。
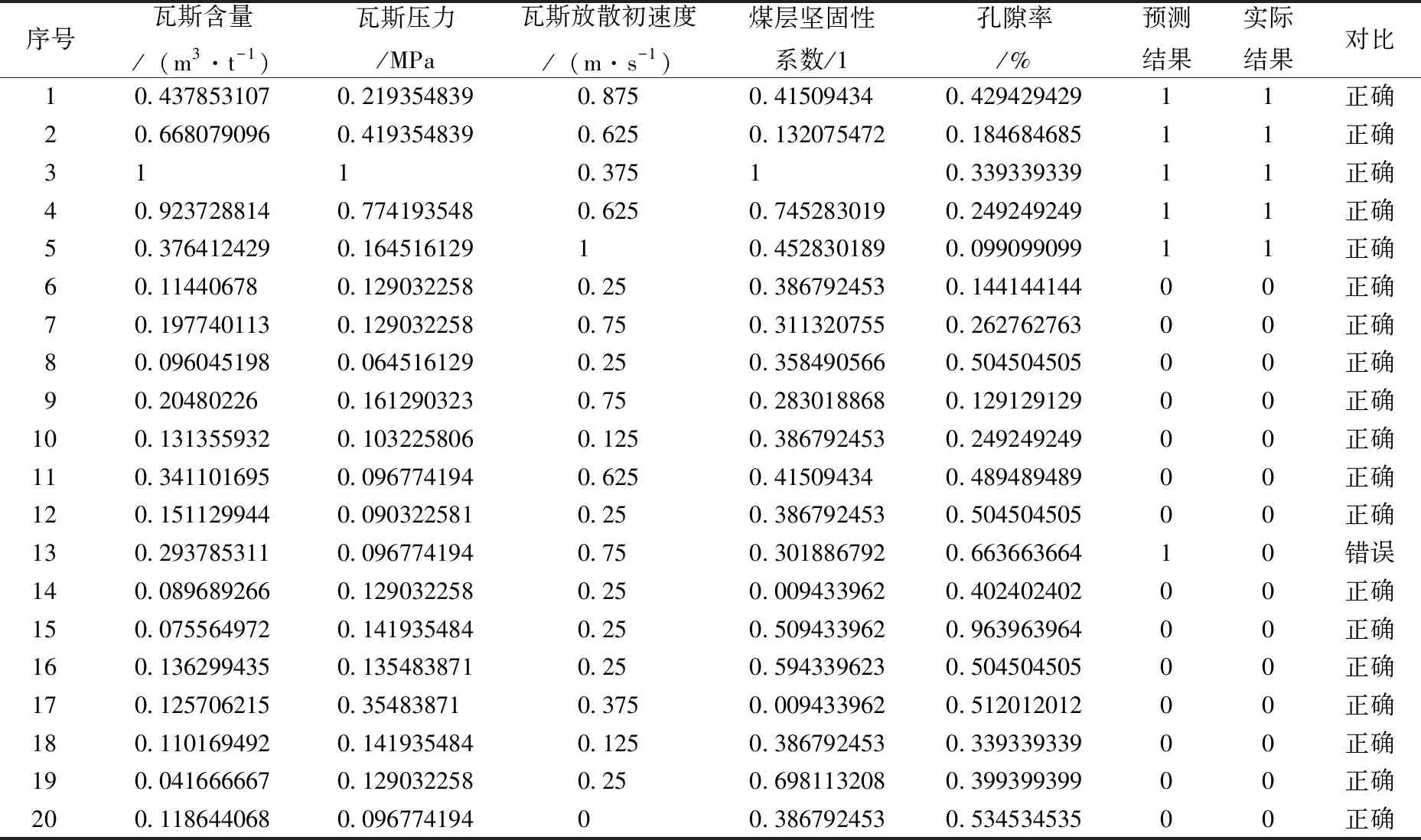
表3 改进PSO算法优化GRNN预测结果
改进PSO算法的预测结果中第13个预测错误,实际突出数据的预测准确率为100%,实际不突出数据的预测准确率为93.3%,总体预测准确率为95%。
基于改进PSO算法优化GRNN的预测收敛图如图2所示,算法从第3代快速收敛,在第40代完全收敛到最佳光滑因子,表明该算法收敛速度快,收敛精度高,能快速找到最佳参数。
7 结语
GRNN有很强的非线性预测能力和泛化能力,网络结构简单,学习速度快,有很好的全局收敛性,非常适合煤与瓦斯突出预测。改进PSO算法将自适应惯性权重和线性调整学习因子结合,平衡了个体粒子的全局以及局部搜索能力。使用基于改进PSO算法优化的GRNN模型对煤与瓦斯突出危险性进行预测,试验结果表明,改进PSO算法优于FOA和PSO算法,不仅克服了算法易于陷入局部最优的问题,还提高了预测的准确率和泛化能力;整体预测结果准确率较高,能满足煤矿安全生产的需要。该模型在煤与瓦斯突出预测方面有良好的前景,对煤矿安全生产有一定的指导意义。
