Numerical investigation of dynamic interaction with projectile and harmonic behaviour for T-finned machine gun barrels

Ekansh Chaturvedi

Maulana Azad National Institute of Technology, Bhopal 462003, India

Keywords:FSHP Machine guns Pseudo-I section Second order mesh Transient behaviour

ABSTRACT Machine gun barrels differ from their rifle counterparts in terms of profile. To support high rates of sustained fire,machine gun barrels are made thicker in order to dissipate more heat and maintain their flexural rigidity and thus accuracy,but on other hand they also contribute in weight addition to weapon.This investigation deals with comparison between a conventional machine gun barrel and an improved innovative design having T-fins, both having same weight and chambered in 5.56×45 NATO ammunition,to compare their structural and harmonic characteristics which were parameterized by factors such as modal spectrum, directional deformation at muzzle ends during a single shot fire and harmonic behaviour at corresponding range of exciting frequencies. The solid models of both the barrels having same weight, were created using Solidworks. The continuous input data functions were generated by MATLAB using the field tested discreet data points. The generated velocity-distance functions were converted into time dependent functions using integration algorithms to calculate transient parameters such as time steps,excitation frequency range,angle of rotation of projectile and its angular velocity.The dynamic condition simulated the varying nature of forces due to eccentricity in projectile and this data was fed to a time step study using ANSYS transient structural work bench followed by modal and harmonic analysis.The results showed a significant reduction in muzzle end deformation which thus proved that the T-finned barrel, although had same weight as that of the conventional one, but had better structural and harmonic characteristics, and hence it would inherit better firing accuracy.

1. Introduction

The issue of vibrations in barrels has always been a consideration of utmost importance as far as arms design is concerned.The amplitude attained by the end of the vibrating barrel directly influences the accuracy of the gun.Particularly,this problem becomes further magnified in case of machine guns because they are built to operate on high firing rates for longer durations, as compared to assault rifle/rifles chambered in same ammunition. The machine gun barrels,therefore,have a thicker profile than their rifle/assault rifle counterparts in order to maintain flexural rigidity and to dissipate the tremendous amount of heat thus generated. The factors [1,2] that influence the accuracy of barrels are the manufacturing tolerances, such as the straightness of the barrel bore,uniformity of the geometry of the barrel,the variations in the width of lands and in the depth of grooves and also the surface finish.These effects get further amplified at higher temperatures as the end sag in barrels increases [3,4].

Kathe et al.performed a barrel study on hybrid electromagnetic/gas gun [5], and concluded that the barrel vibrations are have a magnified impact in recoil loading guns in which,unlike gas launch,the load is applied at the muzzle end rather than at breech end.This effectively simulates a situation of barrel under columnar compression resulting in phenomenon called barrel whip. The interaction of projectile with barrel, as explained in the following section, is basically a moving mass problem on a cantilever beam,which indeed is the barrel itself. The accurate solution of moving mass problems has been facilitated via the use of computational methods, and the study [6] (2010) has compared numerical methods for response of beams, while the Ataei et al. [7] and Nikhoo et al. [8] have studied the modal characteristics of beams under the effect of a moving mass.

Fig.1. Conventional machine gun barrel 5.56×45 mm [10].

The moving load problem is also vital for defense industries in order to provide an accurate shooting for Cannons,and the study by Tawfik[9](2008)is valuable for the effects of an unbalanced mass of a projectile on the vibration of a barrel.

Therefore, the problem regarding barrel's current design,considering the heat dissipation, weight and rigidity as factors of primary importance,may be split into two parts:the barrel requires modification to increase dissipation of heat and the barrel requires to be stiffened further for retaining accuracy; and these two problems need to be solved without increment in weight.

The presented solution proposes to reduce the base diameter of middle portion of a conventional barrel shown in Fig.1[10]and to add even number of T cross sectioned fins along that length as shown in Fig. 2, which has same weight as that of conventional barrel, i.e.1042.93 g. Incorporating the even number of fins would ensure that two fins are diametrically opposite to each other and this formation would formulate a pseudo-I section. Since the I-section has the greatest section modulus per unit weight,and thus the flexural rigidity,it may be incorporated in a feasible manner to enhance the flexural rigidity of barrels.Moreover,the increment in surface area subjected to atmosphere due to fins would improve the heat dissipation capability of the barrel.

A 2018 based investigation[10]found out that the introduction of T-fins enhanced the heat dissipation capability and stiffness of the barrel along with reduction in weight, although the aspects of harmonic excitations were not covered.Hence,investigation of the modal spectrum of refined structures becomes necessary to declare a particular design superior over another.The study[11]conducted over tank barrels portrayed the consequences of vibrations in long barrels.This concluded that the gun system having a longer barrel if not controlled properly, may deflect up to 6 times of the one with the short barrel and may result in poor first shot hit probability(FSHP).

Pyka et al.[12]experimented with a fiber reinforced composite barrel, constituting carbon fiber as reinforcing element. Though it was found to have increased the stiffness significantly but using carbon fiber composite for mass production of barrels is still an expensive methodology. Moreover, stability of carbon fiber composite at higher temperatures is a significant factor when put to use with gun barrels as it is heavily dependent on the epoxy types used as matrix. Where most epoxies start degrading around 300°C(Epidian 5 mentioned in Ref.[12]has a glass transition temperature 171°C [13]), steel is undoubtedly more suitable material for such applications.

Considering the dynamic nature of interior ballistics; the geometric configuration of the projectile and grooves, twist rate in particular,also decide the magnitude and directions of forces acting over the barrel. For simplification, the two major forces that act over barrel are the weight of the projectile and centrifugal force generated by mass eccentricity present in it, which being a manufacturing aspect,shall not be ignored.Thus,this investigation intends to cover all the aforementioned dynamic aspects through a simplified methodology which uses curve-fitting techniques and FEM simulations.

Fig. 2. Modified T finned machine gun barrel 5.56×45 mm.

2. Methodology and analysis

An ingenious attempt to reduce the gun barrel vibrations in a 120 mm bore barrel by Esen and Koc [14] utilized a passive gun vibration absorber,optimized by a generic algorithm code and the results were compared with those obtained by proposed FEM model.Though the methodology of analysis itself is a novel one but indeed a complex one as well and showed an improvement in accuracy only by 0.5%.Hence,this study adopts FEM approach which is easier to implement.

Yet another very important analysis conducted by Esen and Koc,again on 120 mm bore barrel [15]. The dynamic interaction between a 120 mm smooth-bore tank barrel modelled as a cantilever beam and an accelerating projectile during firing was presented.The inter-action was modelled using a new FEM approach that took into account the projectile's inertia,Coriolis,and centripetal forces and the horizontal and inclined positions of the barrel. The mass,exit velocity and acceleration effects of the projectile on the dynamics of the barrel were investigated. The effects of the projectile's inertia, and Coriolis and centripetal forces were evaluated as well. Furthermore, the tip displacements at different firing angles were determined by transferring the mass, stiffness and damping matrices of the barrel with the addition of the instantaneous property matrices of the projectile from a local coordinate to the global Cartesian coordinate with the aid of transformation matrices. Finally, the barrel vibrations caused by the successive firings were evaluated under different firing scenarios.

It is this particular research work [15] which inspires the presented study,which although has been purposefully conducted for evaluating and comparing the existing and modified designs of machine gun barrels in particular, due to the reasons presented earlier in the introduction section.However,study[15]assumes an average constant acceleration of projectile, which, as can be observed in the sub-section 2.2,is not the most accurate approach.Hence, to account for a non constant acceleration, a resourceful technique of curve fitting was adopted for this study which has been explained in sub-section 2.2.

This analysis was based on input data covered from a field test which was conducted by Dater and Wong [16] for 5.56×45 M855 ammunition to plot its performance characteristics such as acceleration, velocity and pressure decay across the barrel length.

This particular study intends to simulate the vibrational characteristics of a 16 inch barrel chambered in 5.56×45 MIL-STD NATO ammunition, and therefore the corresponding relevant data was taken from the referenced study.

2.1. Dynamics of barrel-projectile interaction

Fig. 3. Schematic diagram representing the problem [17].

A machine gun barrel can be assumed as a cantilever Euler beam fixed supported at the breech end. The mass of projectilemand rotational inertiaJis continuously changing its position with respect to time and hence this situation simplifies to a moving mass load problem as shown in Fig. 3 [17]. The problem further complicates because of presence of a manufacturing defect called eccentricity in the bullet because the projectile rotates along the rifling grooves present in the barrel, as a reason which imparts centrifugal force on the walls of inner surface[15,17].It is to be kept in mind that this force is constantly changing its direction and magnitude as well due to accelerated motion.

Setting gun barrel=l,cross-sectional area=A, material density=ρ,and flexural rigidity=EI,and projectile mass=m,damping attenuation coefficient=H; angular velocity=ω and eccentricity=r; flexural vibration equations of the gun barrel alongYaxis andZaxis respectively are:

Where ω represents the angular velocity at timetandris the eccentricity radius. It is to be noted here that the term δ（x-vt）represents Dirac delta function associated with Eq. (1) and Eq. (2)[18,19].

The Dirac delta function (also known as the impulse function)can be defined as the limiting form of the unit pulse δT(t) as the durationTapproaches zero [20]. As the durationTof δT(t) decreases, the amplitude of the pulse increases to maintain the requirement of unit area under the function, and

This function may be analytically solved by modal expansion method [18,19] or Duhamel's convolution integral [20,21], both being applicable but they require certain assumptions to be brought in consideration which might not give accurate results.For instance, another study conducted on tank barrels [17] assumed projectile to be moving inside the barrel with a constant acceleration and the equation was resolved to components of acceleration as follows:

Where, first item on the right of Eq. (4) is the convected acceleration of the gun barrel, the second item is Coriolis acceleration caused by the moving load, the third item is centripetal acceleration,and the fourth item is normal component of acceleration.The same mathematical modelling,considering this problem as that of a moving mass one, was also used by Esen et al. [22], where they combined the FEM with ANN(artificial neural network) to resolve the non linearity in the problem.

The expressions on the right hand sides of Eq. (1) and Eq. (2)represent the forces resulting from projectile's interaction with the barrel.However,these forces not only produce deformations in the barrel, as governed by Eq. (1) and Eq. (2), but also work as excitation elements to produce vibrations which can be represented as the general equation as follows [15,22]:

where;

where [M], [C] and [K] are, respectively, the instantaneous overall mass, damping and stiffness matrices. Besides, F(t) is the overall external force vector andsis the overall displacement vector of the system at timet.

Here the beam mass matrix is evaluated by

whereN(x) are the beam interpolation polynomials andTis the total instantaneous kinetic energy of the bullet-barrel system,when bullet is at a positionxfrom the origin of motion [9]. The effective bullet mass,m, matrix is evaluated at the bullet position as:

while the beam stiffness matrix is evaluated by:

The effective geometric bullet stiffness matrix is evaluated at the bullet position as:

For the obtaining the matrices of [M], [K], and [C], one can determine the elemental property matrices;and then can assemble them properly using the conventional FEM approach.For a detailed understanding of determination of matrices, one may refer to the study conducted by Esen et al.[23].where,a similar mathematical model as constructed in this work was resolved into 2-D transverse forces and corresponding displacements were calculated by applying FEM. It is to be noted that the study [23] does consider rotating moment imparted by the projectile over the barrel. However, this has been ignored in this study as 5.56×45 mm ammunition is a very small projectile as compared to 120 mm projectile used in study[23]and hence the rotational moment is of negligible magnitude to be of any significance as far as the purpose of this investigation is concerned.

Regarding the assumptions particular to considering a constant average acceleration of projectile by Refs. [15,22and23] the data plotted in Ref.[16]does not entail the aforementioned assumption for internal ballistics of firearms and hence the dependence of velocity of projectile over the length of distance covered within the barrel requires some specified function to generate subsequent data for simulation.

2.2. Input data generation through MATLAB

Fig. 4. Experimentally plotted velocity variation with barrel length [16].

Table 1 Values taken from Fig.4 corresponding to a 16 inch barrel(in SI units).

Fig. 5. Velocity-length plot as generated function.

Fig.4 shows the plot referred from Dater and Wong's study[16]relating velocity acquired by the projectile to the barrel length.For generating input function,seven points as tabulated in Table 1 were taken corresponding to a 16 inch (406.4 mm) barrel and a five degree curve was fit using MATLAB,as shown in Fig.5,where velocity is in meter per second and length covered in barrel is in millimeters.

The five degree polynomial function, as projected in Fig. 5 turned out to be as follows,

Where,xis the distance covered by bullet from the breech end where the bullet resides at the timet=0. The programming of dynamic model simulation requires specific time points to determine the angle of rotation of bullet by that time and hence the relative position of the actual centre of mass of the eccentric bullet.By the general equation of motion,time function was derived from Eq. (12) as follows,

Eq. (8) provided the velocity curve, i.e. variation of distancexwith timetas shown in Fig. 6.

The values thus obtained from Eq. (13) were further used to generatev-tcharacteristics as shown in Fig. 7. Thev-tequation turned out to be as follows:

It can be clearly observed from Fig. 7 that the slope, i.e. acceleration (a), of projectile varies drastically with time as shown in Fig. 8, and hence the assumption of considering acceleration a constant value[17]may not be a very precise approach,specifically when dealing with comparatively low mass high velocity projectiles. The drop in acceleration can be accounted by the randomness associated to the highly turbulent and fast burning propellant combustion inside the barrel.

Fig. 6. x-t characteristics for 5.56×45 mm ammunition.

Fig. 7. v-t characteristics for 5.56×45 mm ammunition.

Fig. 8. a-t characteristics for 5.56×45 mm ammunition.

The spin provided to the bullet by the rifling grooves depends over the twist rate. The standardized twist rate for a 62 grain(4.02 g) 5.56×45 mm ammunition is 1 complete revolution in 8 inches of barrel travel[24].TheRPMof the spinning bullet at a timetwould further depend on the linear velocity of the bulletvas follows [14]:

where,vis velocity in feet per second and η is the twist in inches.Hence the angular velocity ω varies withRPMas follows:

This gives,

Considering η as 8 inches, we have

For determining the exact position of the centre of mass at a time t,it seems necessary to calculate the specific angle ϴthe bullet has turned by that time. The function ϴis derived as follows:

where,ω（t） is the function derived from Eq. (18).

The integrations were performed using in-built MATLAB algorithm and the resulted function determining ϴin radians with timetis shown in Fig. 9.

Subsequently,the lateral and longitudinal components of forces imparted by bullet to the barrel,as represented at the right side of Eq. (1) and Eq. (2), were calculated individually corresponding to the seven distance (or time) domains as tabulated in Table 1. The eccentricityrwas assumed to be 0.03% of the actual radius as a result of general standard deviation [25] and the bullet was assumed to be a standard 62 grain (4.02 g) projectile. These forces are tabulated in Table 2 as follows:

The significance of minus sign before the values of forces has been further clarified in section 2.3. The generated data as discussed in the preceding section was fed to transient structural work bench in ANSYS multi-physics simulation software.

Fig. 9. ϴ-t characteristics for 5.56×45 mm ammunition.

Table 2 Forces imparted by bullet's interaction with barrel.

2.3. Modelling and simulation

The solid models of both the barrels shown in Figs.1 and 2 were built in Solidworks modelling software. The weight of both the barrels was kept same,i.e.1042.93 g with AISI 4340 annealed steel[10]. Table 3 shows the mechanical properties of the material.

The solid models were transferred to ANSYS modal workbench to identify the first 12 mode-shifts as their structural characteristics[26]. The second order mesh [27] thus generated for both the models consisted of 103404 nodes and 342414 elements.In order to achieve precision, mesh refinement was specifically applied near the muzzle end of the barrels. As an initial pre-requisite, both the barrel models were provided a fixed support at the breech end as exemplified in Fig. 10 with a conventional thick profile barrel[28,29]. The results of the modal analysis have been discussed in depth in section 3.

Proceeding to the transient structural analysis, the stepcontrolled data input consisted of seven steps each distributed in time domain according to Table 2. The solid models of barrels had been provided with separately interacting solid protrusions over the bore surface as shown in Fig.11, for imparting forces as tabulated in Table 2.These surfaces were discreetly modelled such that they are away from each other by the distance as tabulated in Table 2.

Table 3 Properties of AISI 4340 annealed steel [10].

Fig.10. Fixed support provided at the breech end.

Fig. 12 clarifies the significance of minus signs in Table 2. The coordinate system used in the software demands force components to be aligned with it. Hence, the minus sign signifies the opposite direction to the arrow as shown in Fig.12.

The assumptions that were considered while building this simulation are mentioned as follows:

1. The effect of pressure variation was ignored as the study focuses on bullet-barrel interaction.

2. The axis of bullet was assumed to be parallel to the barrel axis at all the moments of time [30].

Fig.11. Interacting protruding surfaces modelled for applying stepped forces.

Fig.12. Default co-ordinate system of the software.

3. The step division into 7 domains would form an almost continuous time dependent dynamic load, although it can be made more precise by increasing the no. of steps.

4. Effect of gas block, gas tube and other gun accessories were neglected.

5. The gravity acted in negative Y direction.

6. The bullet's torsional reaction over the barrel was assumed negligible and thus was not considered.

At last,proceeding to the harmonic analysis,the simulation prerequisites were the excitation frequency range lied within slightly extended range of 600 Hz-1500 Hz, which corresponds to the range of first 6 modes of vibrations,which are most dominant in the case of barrels [31] under the force of gravity and transient load together combined; because according to Dirac's function, the continuously changing force vector is made up of many infinitesimally small impulses [21]. It is important to mention that the damping effects were ignored as they would be irrelevant for what this particular study intends to find.

3. Results

3.1. Modal analysis results

Fig. 13 shows the first 12 modal frequencies of plain conventional barrel and modified T-finned barrel respectively. It could be clearly visualized from Fig.13 that the simulated modal spectrum of T-finned barrel had a forward shift from that of the conventional barrel.

3.2. Transient structural analysis results

The transient analysis results exhibited a clear comparison between the deciding parameters of both the barrel models. These deciding parameters include directional deformation at the muzzle end along lateral and longitudinal directions, and the equivalent Von Misses stress contours over the barrel bodies.

Fig.14 and Fig.15 show the directional deformation along Y axis for conventional thick profile barrel and the modified T-finned barrel respectively.It can be clearly observed that the muzzle end of the T-finned barrel deformed to a far lesser extent than that of conventional barrel.The percentage reduction Δ can be calculated as follows:

Fig.13. Modal spectrum distribution of the barrels.

Fig.14. Longitudinal deformation in conventional barrel.

Fig.15. Longitudinal deformation in T-finned barrel.

where,DcandDtrepresent muzzle end deformation in conventional barrel and T-finned barrel respectively.

Following Eq. (13), the reduction in deformation percentage is,

The solution (21) clearly shows that the reduction in barrel deformation is exceptional in case of modified T-finned barrel.

Similarly, Fig.16 and Fig.17 show the muzzle end deviation in conventional and modified barrel along Z axis respectively.Following Eq. (20) again, the reduction in lateral deviation is.

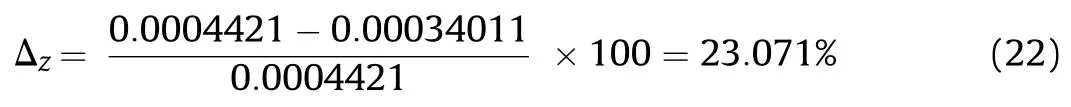
Fig.16. Lateral muzzle deviation in conventional barrel.

Fig.17. Lateral muzzle deviation in T-finned barrel.

Fig.18. Equivalent stresses in conventional barrel.

Fig.19. Equivalent stresses in T-finned barrel.

From solution (22), a 23% reduction in muzzle deviation may also be considered as a significant, if not drastic, improvement in barrel design for retaining the precision while firing.

Fig.18 and Fig.19 show the Von Misses stress contours over the conventional and T-finned barrel bodies respectively.A comparison at a glance clarifies that the modified barrel stressed lesser than the conventional thick barrel.

3.3. Harmonic analysis results

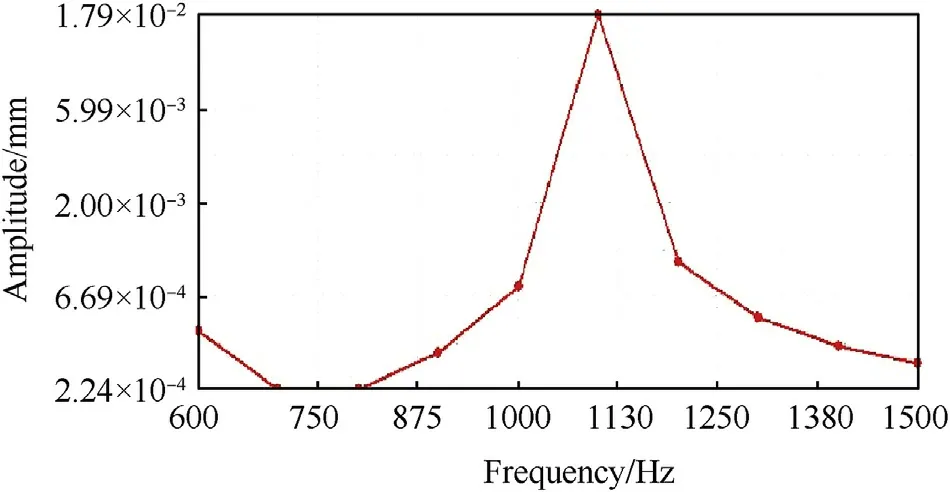
Fig. 20. FRF response for conventional barrel along Y axis.

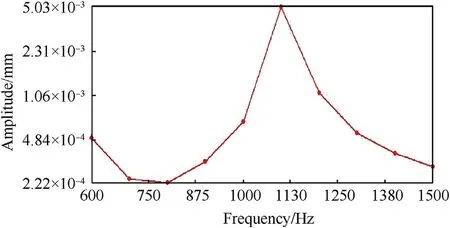
Fig. 21. FRF response for T-finned barrel along Y axis.

Fig. 20 and Fig. 21 show the FRF (frequency response function)along Y axis for conventional and T-finned barrels respectively.

It was observed that maximum amplitude of 0.017942 mm in conventional barrel occurred at 1100 Hz(dominant mode)and the corresponding value of 0.001094 mm in T-finned barrel at 1200 Hz.Therefore,a shift by 100 Hz in right direction was observed.

Fig. 22. FRF response for conventional barrel along Z axis.

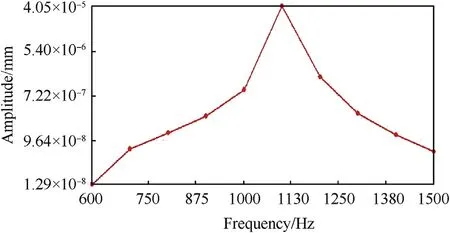
Fig. 23. FRF response for T-finned barrel along Z axis.

Similarly,Figs.22 and 23 show the FRF response along Z axis for conventional and T-finned barrels respectively.

Along Z axis, it was observed that maximum amplitude of 0.00015449 mm in conventional barrel and 0.000040461 mm in T-finned barrel occurred at 1100 Hz.Though no shift was observed in dominant modes but a significant reduction in amplitude of vibration, which directly influences accuracy, was observed.

4. Conclusions

1. The results were in found to be in agreement with the expectations from the improved design of a machine gun barrel. A significant improvement in dynamic structural and harmonic properties was observed in T-finned barrels.

2. For simplifying the simulation setting procedure and reducing calculation time, the geometry was simplified and the effects of gas-block, gas-tube, muzzle devices etc, were not taken into consideration. The major cause of vibrations was assumed to be the interaction between bullet and the barrel.

3. Due to factors affecting manufacturability, the extension of fins was halted at the mid length, i.e. where the gas block attaches (in case of a gas operated weapon). Results may indeed vary with different lengths of fin extension.

4. The eccentricity of bullets was taken into consideration.The magnitude of forces thus calculated showed that it is indeed a critical parameter for accurate firing.

5. Barrels were modelled such that they had same weight for same material. Nevertheless, the T-finned barrel, forming a pseudo-I section proved to be a better alternative for retaining accuracy and precision in barrels; subjected to same loading conditions.

6. Figs. 14-17 showed that there was a quantitatively significant reduction in muzzle end deviation, which indicates an improved FSHP figure of the weapon with T-finned barrels.

7. The FRF responses showed that the dominant excitation spectrum lied between 1000 Hz and 1250 Hz. This showed that barrels are more likely to fail between these ranges of harmonic loading; although machine guns chambered in medium sized cartridge such as 5.56×45 mm never operate at such firing rates.

8. Harmonic analysis also conveyed the superior design of T-finned barrel,indicated with considerably less deviation.

9. The stress analysis results also indicated that the T-finned barrel gets an edge over the conventional barrel, which further indicates a longer structural life. All these structural improvements suggest a very interesting point that for acquiring same characteristics as of a conventional barrel, a lighter T-finned barrel would be required; which would further result in a lighter and more effective weapon.

10. Figs. 1 and 2 show visible differences in barrel profiles. A keen eye may quickly estimate the differences in manufacturing processes required to fabricate the two types of barrels.Hence,a detailed DFM(design for manufacturing)study would further be required to bring the modified T-fnined barrel as a commercial success.

Acknowledgements

This research work was a result of insight and expertise provided by Mr.Ian McCollum who is the Editor at ForgottenWeapons.com; and the Technical Advisor at Association of Firearm and Tool mark Examiners(AFTE).The author expresses his deep gratitude to Mr. McCollum and Faxon Firearms for assisting in the research by providing valuable knowledge through ForgottenWeapons.com,though they may or may not agree with all of the interpretations and conclusions of this paper.