Study on performance degradation and failure analysis of machine gun barrel
2020-05-23XiaolongLiLeiMuYongZangQinQin
Xiaolong Li, Lei Mu, Yong Zang, Qin Qin
School of Mechanical Engineering, University of Science and Technology Beijing, Beijing,100083, China
Keywords:Wear of the inner wall Accelerated life test Numerical simulation Ballistic performance End of the barrel life
ABSTRACT An increase in the use of the gun barrel will cause wear of the inner wall, which reduces the muzzle velocity and the spin rate of the projectile.The off-bore flight attitude and trajectory of the projectile also change, affecting the shooting power and the accuracy. Exterior ballistic data of a high-speed spinning projectile are required to study the performance change.Therefore,based on the barrel's accelerated life test, the whole process of projectile shooting is reproduced using numerical simulation technology, and key information on the ballistic performance change at each shooting stage are acquired. Studies have shown that in the later stages of barrel shooting,the accuracy of shooting has not decreased significantly.However,it is found that the angle of attack of the projectile increases as the wear of the barrel increases.The maximum angle of attack reaches 0.106 rad when the number of shots reaches 4300. Meanwhile,elliptical bullet hole has appeared on the target at this shooting stage. Through combining external ballistic theory with simulation results, the primary reason of this phenomenon is found to be a significant decrease in the muzzle spin rate of the projectile. At the end of the barrel life, the projectile muzzle spin rate is 57.5% lower than that of a barrel without wear.
1. Introduction
Wear in the inside of a barrel can lower the restraint and guiding effect of the interior ballistics on a projectile,which further results in negative effects on the exterior ballistic performance parameters of the projectile, such as projectile velocity, flight attitude, and shooting accuracy. Therefore, the degradation mechanism of the ballistic performance can be effectively grasped by studying and analyzing the various performance parameters of the projectile's external flight,and the service life of the gun can be improved in a targeted manner.
High-speed flight tests based on special experimental devices have been widely used to investigate the ballistic performance of the projectiles in question.At present,experimental studies on the flight attitude and trajectory of a projectile primarily rely on the image acquisition method [1-3], the photoelectric detection method[4,5],and the sensor telemetry method[6].Generally,these methods are endowed with high measurement accuracies. However, the associated devices usually incur relatively high operation and maintenance costs.Additionally,they have to be coupled with specialized post-processing software for data analysis. To circumvent this predicament,a relatively complete theoretical framework for describing the exterior ballistic behavior of a projectile has been established with the help of traditional theoretical mechanics,aerodynamics, and other disciplines [7-9]. As for the problem of the ballistic trajectory with a long range, the projectile can be approximated to be a small particle without considering its special geometrical features, which helps in developing its corresponding mathematical trajectory model, as exemplified in Refs. [10,11].However, it is necessary to carefully consider the geometrical features of a projectile when its motion attitude is the main concern.Currently, deviations between theoretically calculated and experimentally measured projectile trajectories still exist owing to a number of reasons, which stresses the need to improve current theoretical frameworks to obtain more accurate predictions[12].
With the continuous improvement in computer technology,numerical simulation has become an efficient and economical tool to study the aerodynamic characteristics, the stability, and the flight path of the projectile, especially for its interior and exterior ballistic performance. Effects of slug material [13], rotating band construction [14,15] on the ballistic performance and dynamic analysis of gun barrel[16-19]have been discussed with the help of finite element analysis(FEA).For small caliber pistols,S.Deng et al.[20,21] performed FEA on the motion of the projectile in a barrel bore. The model accurately reflected the rotation, nicking, and stress of the projectile.Based on computational fluid dynamics,the effects on aerodynamic coefficients such as projectile structure[22,23],projectile-solid surface distance[24],the muzzle velocity of the projectile [25], and the Magnus torque of the projectile [26]have been studied. In light of the fact that the projectile demonstrates little deformation during its off-bore flight, it can be assumed to be a rigid body. Based on this assumption, Leonard C.et al.[27]established an optimized projectile linear theory for rapid prediction of projectile trajectories. Gao et al. [28] considered the interaction between the missile's nose and body; an integrated rigid dynamic model of a deflectable nose missile was set up by using rootless multi-rigid-body system dynamics in the quasi-body coordinates.Zhang et al.[29]described the laws on the impact of an exterior ballistic trajectory by the deflection of the nose of the missile. Based on the coupled computational fluid dynamics/rigid body dynamics technique, J. Sahu [30] achieved flight trajectory simulations for a supersonic wing projectile and a subsonic spinning projectile. In a previous study by Scheuermann E. et al. [31],the microspoiler control mechanism of a highly maneuverable projectile was systematically investigated.
To clarify the ballistic performance degradation mechanism,overcome the inherent defects of the barrel, and ultimately optimize the barrel life, a reasonable establishment of the correlation between the worn machine gun barrel and the ballistic performance is required. This aspect has not been reported in the literature and thus constitutes the main objective of the current study.To this end, a worn gun barrel model is proposed in conjunction with an accelerated life test. With the help of classic exterior ballistic aerodynamics theory,the muzzle velocity and spin rate of the projectile,as well as the flight attitude and the dispersion intensity,are studied. The prediction of the proposed model matches well with the actual test data. The current study could help shed light upon the intrinsic reason responsible for the barrel life. Additionally, the established methodology could benefit the prediction of ballistic performance under different levels of barrel wear.
2. Accelerated life test
2.1. Failure criteria of the gun barrel
The barrel life is a key parameter of an automatic weapon, it represents the total number of bullets shot by the automatic weapon until it no longer satisfies the requirement of ballistic performance. To determine the life of the machine gun barrel, the following barrel failure criteria were used:
(1) Muzzle velocity-based criterion(MBC).The coil target is used to measure the muzzle velocity. The muzzle velocity is measured at each stage of the life test. The average value is obtained by measuring 10 rounds each time. Barrel failure occurs when a decrease of 15%in muzzle velocity is observed with respect to the original value.
(2) Elliptical bullet hole ratio-based criterion (EBC). When the ratio of the major axis to the minor axis of the bullet hole on the target is greater than 1.25,it is considered as an elliptical bullet hole.Taking 20 rounds as a group,when the elliptical bullet hole ratio exceeds 50% of the number of shots, it is determined that the barrel is invalid.
(3) Dispersion intensity-based criterion(DBC).Three groups(20 rounds per group) are fired continuously on the ground target, and the average radius of the 50% projectile (R50) is taken.The dispersion intensity at the end of the barrel life is taken as the continuous three-target average,R50≥300 mm.
2.2. Test data
Accelerated life test on a 12.7 mm caliber machine gun was carried out using the standard firing code [32], to study the life trend for machine gun barrels.The mechanical properties of barrel material are shown in Table 1. The muzzle velocity drop rate, the elliptical bullet hole rate and the dispersion intensity were evaluated after a certain number of shots to determine whether the barrel meets the failure criterion.
Fig. 1 is a sectional-view sketch of the barrel structure. The rifling starting point was defined as the rear part of barrel and the outlet of barrel was defined as the front part. In the process of the barrel accelerated life test,the rear part of the barrel,especially the rifling starting point,endured the strong extrusion effects of hightemperature and high-pressure gunpowder gas,and the actions of the projectile during the shooting process. With the increase in number of projectiles, the chromium layer was seriously eroded,and the matrix material began to show signs of serious scouring ditches,as shown in Fig.2.The projectile caused wear of the rifling during it moving in the barrel. The front part of the end-of-life barrel was severely worn and the caliber was significantly increased. It was also found that bore exit of the worn barrel was elliptical, as shown in Fig. 3.
The axial wear of the bore could be divided into three basicareas,namely,the severe wear zone,the slight wear zone,and the muzzle wear zone.Due to the high temperature and pressure of the gunpowder gas and the projectile extrusion,the chromium layer on the back of the barrel typically eroded seriously,displaying obvious erosion ditches. This was the serious wear zone. The inner surface of the front part of the barrel was partially cracked, and the intersection between land and groove lines was accompanied by small pieces of the chromium layer eroding away. This was the muzzle wear zone. The middle part of the barrel was a slight wear zone,which showed only slight erosion and uniform wear.In the life test,the change in bore groove line diameter in the barrel was measured using different caliber gauges,and the depth of entry of each gauge was recorded.The wear data for the bore at each shooting stage is shown in Fig.4.The length of the serious wear zone along the axis of the barrel was shorter,while the length of the muzzle wear zone exceeded half of the barrel length. The data points for the severe wear zone and slight wear zone were basically linear distributions,while the data points for the muzzle wear zone were relatively scattered,which indicated that there was uneven wear and drumshaped deformation within the bore. Considering the radial constraints of the projectile when it was out of the bore, and for the convenience of subsequent modeling,the first and last data points for the muzzle wear zone were connected using a linear fitting method.The maximum relative error for the four firing stages was only 0.16%, which verified the accuracy of the fitting.

Table 1 Mechanical properties of barrel material.

Fig.1. Schematic of gun barrel section.

Fig. 2. Surface topography of rear part of the bore: (a) New barrel; (b) End-of-life barrel [32].

Fig. 3. Front section of the barrel: (a) New barrel; (b) End-of-life barrel [32].
3. Ballistic modeling
3.1. Mesh model
This study carried out parametric modeling based on the Python language for the 12.7 mm caliber rifled barrel, considering the influence of the mesh accuracy of the traditional three-dimensional model when building the barrel wear model (Fig. 5). The specific process can be summarized as follows:
(1) The sectional morphology of the barrel section was established based on the Abaqus software package, and the grid unit was divided.
(2) Based on the Python programming language, the section mesh was stretched to the length of the barrel and each node was rotated according to the rifle helical angle. The number of layers in the axial sliced grid section of the barrel was defined asM, and the axial lengthL′of the barrel corresponding to one cycle of the rifle line rotation can be expressed as:

Then the expression of the rotation angle β′of each layer of the grid is:


Fig. 4. Wear data for the bore.

Fig. 5. Parametric modeling flowchart.
whereLis the full length of the barrel.
(3) Based on the Python programming language, the wear segment nodes were processed by migration. The length of the wear section at the rear of the barrel wasC1, the field angle was θ1, the length of the middle wear section was|C2-C1|, the length of the front wear section was |L-C2|, and the field angle was θ2, as shown in Fig. 6.

Fig. 6. Rifling radius of gun barrel wear.
Then, the radiusriof the rifling line corresponding to each positionCin the axial direction could be expressed as
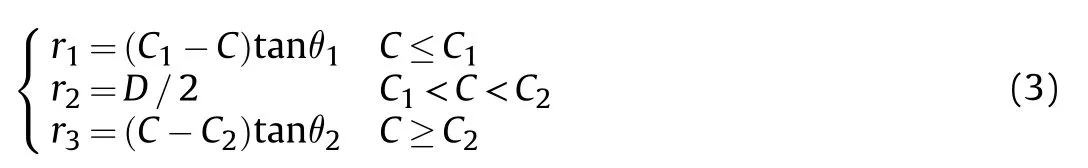
The offset of each node on the inner wall of the corresponding barrel wasD/2-ri.
(4) The mesh model of the worn barrels was shown in Fig. 7. In addition, the projectile mesh was generated based on HyperMesh software, as shown in Fig. 8. Mesh type were hexahedral reduced integral solid element(C3D8R) for both the barrel and projectile.

Fig. 7. Mesh model of the worn barrel.

Fig. 8. Mesh model of the projectile.
3.2. Material properties
The barrel is made of high strength steel, while the projectile shell and the projectile core,respectively,made of copper and steel.The material type in this study is set to isotropic elastic-plastic without failure. The mechanical properties of the relevant materials are shown in Table 2.
3.3. Contact
The “surface-to-surface” contact type is used to define the projectile shell and the inner bore of the barrel. Modern tribology studies suggest that the friction factor is related to the pressure and velocity between the contact surfaces.The surface of the projectile shell melts at a high speed, which changes the lubrication mechanism between the metals.The materials in this study are basically consistent with reference [21,33]. Thus, the dynamic coefficient of friction between the projectile shell and the inner bore is set to 0.1.
3.4. Interior ballistic load
The interior ballistic process includes the engraving process and in-bore motion of the projectile. The radial dimension is significantly increased due to the wear of the barrel.Generally speaking,the engraving pressurep0of the projectile will decrease and the use of propellant energy will be less efficient [34]. Moreover, theprojectile in this study has no driving band, and the band is the main factor that causes the engraving pressure. Therefore, the engraving pressure can be ignored and the initial position of the projectile is assumed to be at the engraving completion point[35].In order to determine the in-bore motion of the projectile, the breech pressurepacting on the bottom of projectile is coupled with an interior ballistic code. The interior ballistic equations are as follows [36,37]:

Table 2 Mechanical properties of the gun barrel and projectile.

where Ψ is the relative burnt mass of the propellant;Zis the relative thickness of the burning gunpowder; χ, λ and μ are the shape-dependent constants of the propellant;u1is the constant burning rate of propellant;e1is the original thickness of propellant;nis the burning rate index;vis the velocity of the projectile;lis the length of travel of the projectile;Sis the cross-sectional area of the worn barrel bore; φ is the secondary power coefficient;mis the mass of the projectile;lΨ is the neck length of the free volume of the chamber;fis the force of the gunpowder explosion;ω is the mass of the propellant;kis the adiabatic index.
Owing to the pressure gradient in the space behind a projectile,a model to describe the relationship between breech pressure and the projectile base pressurepswas proposed [38], as shown in Eq.(5):

where φ1the losses coefficient (for small arms 1.05-1.1).
Based on Eq. (1) and Eq. (2), the interior ballistic calculation is programmed by means of user subroutine VUAMP[35,39],and the fourth-order Runge-Kutta method[40]is used to solve the interior ballistic equations. Coupling with the calculation results of ABAQUS,including the displacement and velocity of the projectile,the base pressurepsof the projectile is acquired.In addition,gravity is applied on the projectile in all phases of computation. Thermal effects including thermal loads are not modeled.
3.5. External ballistic load
The projectile is always subjected to a vertical gravitational force,which equals its weight times the gravitational acceleration.In the plane of the angle of attack,the total aerodynamic forceRcan be decomposed into resistance,Rx, which is along the reverse speed, and lift,Ry, that is perpendicular to the direction of the velocity[41].The external ballistic load of the projectile is illustrated in Fig. 9.
When operating at a supersonic speed,the air resistance applied to the projectile primarily includes the friction drag owing to the air viscosity, the vortex drag generated by the bottom vortex,and the shock wave drag generated by the shock of the warhead.According to aerodynamics theory, the expression of air resistanceRxis:

where ρ is the air density,vthe velocity of the projectile relative to the air,Sthe characteristic area, andcx0the resistance coefficient.The resistance coefficient is the summation of the friction drag coefficientcxf, the vortex drag coefficientcxb, and the shock wave drag coefficientcxw:

When the angle of attack δ is not zero,the drag coefficient is as follows.

wherecy' is the derivative of the lift coefficient.
The lift of the projectile is perpendicular to the relative speed in the plane of the angle of attack,and the expression of the liftRyis:

wherecyis the lift coefficient.
The total aerodynamic forceRcan also be decomposed into an axial forceRAalong the projectile axis and a normal forceRnperpendicular to the projectile axis.The normal force coefficientcnof the projectile can be expressed as the sum of the head normal force coefficientcnn, the tail normal force coefficientcnt, and the viscous normal force coefficientcnf, namely:

When the angle of attack δ is small,the lift coefficientcycan be expressed by the normal force coefficientcnof the projectile:

Fig. 9. Diagram of the off-bore load of the projectile.

Fig.10. Stress distribution of the projectile as it is squeezed into the barrel.

The resistance and lift coefficients are determined according to the projectile structure and the angle of attack at the muzzle.Owing to the short firing distance, the effects of dynamic aerodynamic forces on the projectile are not considered in the model.
4. Verification and discussion
4.1. Posture of the projectile squeezed into the gun
Before the accelerated life test, there was no gap between the bore and the projectile surface. The projectile was in uniform contact with the bore when it was squeezed into the barrel, as shown in Fig. 10(a). Owing to the increase in barrel tail aperture caused by barrel wear,the projectile loses its ideal orientation,and the center of the projectile no longer coincides with that of the barrel. Therefore, as the barrel wear increases, the initial contact area of the projectile and the rifling changes as the projectile is squeezed into the barrel, as shown in Fig. 10(b). This eventually results in an uneven scoring on the projectile and reduced symmetry and roundness.
4.2. Projectile muzzle velocity and spin rate
The muzzle velocity(v)of the projectile at different firing stages is shown in Fig. 11. The maximum relative error between the simulation results and the test data is 1.27%, which verifies the accuracy of the model. The muzzle velocity of the projectile in the unworn barrel is 807 m/s, and when the number of shots reaches 4300, the muzzle velocity of the projectile is 765 m/s. The decline rate of velocity was 5.2%,which did not meet the criteria(MBC)for the end of the barrel.

Fig.11. Muzzle velocity of the projectile.

Fig.12. Muzzle spin rate of the projectile.

Fig.13. Vertical displacement of the projectile head during in-bore flight.

Fig.14. Horizontal displacement of the projectile head during in-bore flight.
In the case where the projectile represents a good contact with the rifling, the spin rate (ω) of the projectile can be theoretically described by ω =v· tanβ/r,where β is the angle of the rifling,andrthe radius of projectile. Note that the current experimental device could not provide a reliable way for measuring the muzzle spin rate of the projectile. Therefore, the muzzle spin rates are only compared between theoretical results and simulation ones, as shown in Fig.12.In fact,the theoretical result is obtained from the previously calculated muzzle velocity (v). It is observed that, in simulations, the muzzle spin rate declined significantly with the increase of wear. This tendency is believed to be caused by the wear-induced degradation caused by the contact between the projectile and the rifling. The muzzle spin rate was 3480.5 rad/s when the number of shots reached 4300, which was 57.5% lower than that of the unworn barrel.
On one hand, the muzzle-velocity of a projectile is negatively affected by an increase in the barrel caliber, which leads to a decrease in the projectile-barrel seal and the base pressure.On the other hand,the radial swing of the projectile in the bore increases the resistance of the projectile to forward movement, which leads to a further decrease in the muzzle velocity of the projectile. The muzzle spin rate decreases with a decrease in muzzle velocity.Meanwhile, owing to the wear on the bore, the mechanical fit between rifling and the projectile becomes progressively worse,along with the guidance constraint, which aggravates the impact on the spin rate of the projectile.

Table 3 Muzzle parameters of the projectile.
4.3. Projectile flight attitude and elliptical bullet hole ratio
The vertical and horizontal displacement curves of the projectile head in the axial movement of the barrel are shown in Fig.13 and Fig.14,respectively.The projectile oscillates vertically when it runs in the bore affected by barrel wear and gravity. The maximum vertical displacement is 0.42 mm at 4300 rounds.Owing to the spin of the projectile in the barrel, the fluctuation in the vertical direction is transmitted to the horizontal direction, and the fluctuation range in the horizontal direction gradually increases. Combined with the swing data in the projectile,it is found that the nutation of the projectile has a certain periodicity. In addition, the vertical displacementy0and the initial angle of attack δ0, when the projectile exits are somewhat random, are related to the wear condition of the barrel, as shown in Table 3.
The overturning moment is dominant among all the air moments, and the angular motion, considering only the overturning moment,is the following equation [41]:

where Δ is the angle of attack,Pis the gyro speed term, which reflects the strength of the gyro effect of the projectile,andMis the overturning moment.
(1) When there is only the initial angle of attack δ0,the angle of attack equation is:

Where,

The maximum amplitude and minimum amplitude of the angle of attack are:

Fig.15. Angle of attack during the projectile off-bore flight.

Table 4 Disturbance parameters.

Fig.16. Tail view of the projectile on the target.

(2) When there is only the initial angle of attack speed δ(·)0,the angle of attack equation is:

The oscillation angular frequency ωdand the amplitude δmwith the arc length as variables are respectively:

The data of the off-bore flight attitude of the projectile were extracted, and the angle of attack of was obtained, as shown in Fig.15.It can be seen from the figure that during exterior ballistics,the angle of attack δmappears to oscillate periodically. The maximum angle of attack increased significantly as the wear of the gun barrel increases. The angle of attack at 4300 rounds was 4.07 times that of 1200 rounds.According to Eq.(15),at the disturbance caused by the initial angle of attack, the maximum angle of attack δmis affected by the initial angle of attack δ0,as well as the tipping momentMand the gyro speed termP.Table 3 shows that the initial angle of attack of the projectile at different firing stages is small and exhibits some randomness. According to Eq. (18), when there is a disturbance caused by the initial angle of attack speed, the maximum angle of attack δmdepends on the ratio of the initial angle of attack and the muzzle velocity (δ(·)0/v0), and the oscillation angle frequency ωd. The data in Table 4 show that δ(·)0/v0is basically the same for the projectiles of each shooting stage,and the oscillation angular frequency ωddecreases from 0.085/m to 0.023/m.Therefore,the reduction in the spin rate of the projectile and the corresponding increase in the overturning moment of the projectile are the fundamental reasons for the significant increase in the angle of attack of the projectile.

Fig.17. Space trajectory of the projectile without gravity.

Fig.18. Space trajectory of the projectile with gravity.

Fig.19. Falling point of the projectile without gravity.

Fig. 20. Falling point of the projectile with gravity.

Fig. 21. Falling point radius and dispersion intensity.
Fig.16 shows the final state of the projectile by simulation when it was fired onto the target. The long and short axis ratios corresponding to each shooting stage were obtained by calculating the lengths of the long and the short axes of the projectile on the target.The long and short axis ratio of the projectile was 1.268(exceeding the threshold of 1.25) at 4300 rounds, which is considered as an elliptical bullet hole. The elliptical bullet hole ratio analysis was carried out on the test gun barrel,and the number of projectiles per group was 20 rounds. The test barrel showed 11 elliptical bullet holes at 4300 rounds, and the elliptical bullet hole ratio was 55%[28], exceeding the 50% index (EBC), as shown in Table 5, and the barrel was declared invalid.Although the simulation cannot reflect the randomness in the actual shooting process, it is in good agreement with the experimental results from the calculated attitude of the projectile target, which verifies the accuracy of the simulation process.
4.4. Projectile trajectory and shooting accuracy
In the simulation, only the shooting elevation angle φ=0 and the aerodynamic hop angle caused by the initial disturbance at the muzzle were considered.In addition,the ballistic trajectory and the projectile placement will be affected by the gravity factor. Therefore, it was divided into two cases, viz., without gravity and with gravity, as shown in Fig.17 and Fig.18, respectively. The condition without gravity can be considered as the elevation angle raised by the shooter during the actual shooting, so that the projectile was closer to the center of the target. The distance between the projectile on the target and the target center was 21.84 mm (without gravity) and 32.57 mm (with gravity) at 4300 rounds, as shown in Fig.19 and Fig.20, respectively.
Dispersion intensity refers to the deviation degree of a group of projectiles' falling point from the dispersion center. The average dispersion intensityR50of the test barrel was 158 mm at 4300 rounds[28],which did not reach the barrel failure criterion(DBC).The simulated falling point of the projectile can only reflect the shooting accuracy of a certain projectile, and it cannot reflect the random phenomenon caused by factors such as the state of the shooter,the shooting environment,and the vibration of the barrel.Although the two concepts are not identical, the falling point(simulation result) and the dispersion intensity (test data) reflect the firing accuracy to a certain extent.Fig.21 shows the falling point radius (distance of the falling point to the target center) and the dispersion intensity at each shooting stage.It can be found that the increase in the number of shots does not cause a significant change in the falling point radius and dispersion intensity of the projectile.This indicates that the wear variation of the test gun barrel has a limited effect on the accuracy of the shot.
5. Conclusions
(1) The projectile collides with the bore owing to the loss of radial positioning when the projectile is squeezed into the worn barrel. This causes the projectile head to oscillate vertically,and the vertical oscillating displacement increases as the degree of wear increases. The maximum vertically displacement is 0.42 mm at 4300 rounds.
(2) Neither the accelerated life test nor the simulation results show that the muzzle velocity of the projectile reached the barrel failure criteria. However, the restriction of rifling on the projectile guidance becomes worse, and the projectile spin rate decreases significantly.The muzzle spin rate ω was 3480.5 rad/s at 4300 rounds, which was 57.5% lower than that of the unworn barrel.
(3) The projectiles showed an increase in the angle of attack at the muzzle of worn barrel with an increase in the number of shots. The angle of attack δmreached a maximum of 0.106 rad at 4300 rounds.The drop in the muzzle spin rate of the projectile reduced its ability to resist flipping, which ultimately led to the elliptical bullet hole ratio exceeding the life threshold.
(4) There is no obvious change in the falling point radius and dispersion intensity during the whole barrel life process.Therefore, the projectile dispersion does not accurately reflect the performance degradation of the test barrel.
Acknowledgments
The present work was financially supported by Beijing Key Laboratory for Corrosion-Erosion and Surface Technology, Beijing Municipal Education Commission Project (SYS100080419).
杂志排行
Defence Technology的其它文章
- A comparison of the ballistic behaviour of conventionally sintered and additively manufactured alumina
- Effect of operating temperature on aged single lap bonded joints
- Investigation on energy output structure of explosives near-ground explosion
- Characteristics structure analysis on debris cloud in the hypervelocity impact of disk projectile on thin plate
- A fast-running method for blast load prediction shielding by a protective barrier
- Coating processes towards selective laser sintering of energetic material composites
